0 rəqəmi real ədədlər dünyasını xəyali və ya mənfi olanlardan ayıran müəyyən bir sərhəd kimi təsəvvür edilə bilər. Birmənalı olmayan mövqeyə görə, bu ədədi dəyəri olan bir çox əməliyyatlar riyazi məntiqə tabe olmur. Sıfıra bölmənin qeyri-mümkünlüyü bunun bariz nümunəsidir. Və icazə verilən arifmetik əməliyyatlar sıfır ilə ümumi qəbul edilmiş təriflərdən istifadə etməklə edilə bilər.

Sıfırın tarixi

Sıfır bütün standart say sistemlərində istinad nöqtəsidir. Avropalılar bu rəqəmdən nisbətən yaxınlarda istifadə etməyə başladılar, lakin qədim Hindistanın müdrikləri boş rəqəmdən avropalı riyaziyyatçılar tərəfindən müntəzəm olaraq istifadə edilməzdən min il əvvəl sıfırdan istifadə edirdilər. Hindlilərdən əvvəl də sıfır Maya ədədi sistemində məcburi dəyər idi. Bu amerikalılar duodecimal say sistemindən istifadə edirdilər və hər ayın birinci günü sıfırla başlayırdı. Maraqlıdır ki, mayyalılar arasında “sıfır” işarəsi “sonsuzluq” işarəsi ilə tamamilə üst-üstə düşür. Beləliklə, qədim Mayyalılar bu kəmiyyətlərin eyni və bilinməz olduğu qənaətinə gəldilər.

Sıfırla riyazi əməliyyatlar

Sıfırla standart riyazi əməliyyatlar bir neçə qaydaya endirilə bilər.

Əlavə: ixtiyari ədədə sıfır əlavə etsəniz, onun dəyərini dəyişməyəcək (0+x=x).

Çıxarma: İstənilən ədəddən sıfır çıxdıqda çıxılanın qiyməti dəyişməz qalır (x-0=x).

Vurma: İstənilən ədədi 0-a vuranda 0 (a*0=0) əmələ gəlir.

Bölmə: Sıfırı sıfıra bərabər olmayan istənilən ədədə bölmək olar. Bu halda, belə bir kəsrin dəyəri 0 olacaq. Və sıfıra bölmək qadağandır.

Ekponentasiya. Bu hərəkət istənilən nömrə ilə edilə bilər. Sıfır gücünə qaldırılan ixtiyari bir ədəd 1 (x 0 =1) verəcəkdir.

İstənilən gücə sıfır 0-a bərabərdir (0 a = 0).

Bu halda dərhal bir ziddiyyət yaranır: 0 0 ifadəsinin mənası yoxdur.

Riyaziyyatın paradoksları

Bir çox insan məktəbdən bilir ki, sıfıra bölmək mümkün deyil. Amma nədənsə belə bir qadağanın səbəbini izah etmək mümkün deyil. Əslində, niyə sıfıra bölmək düsturu yoxdur, amma bu rəqəmlə digər hərəkətlər olduqca ağlabatan və mümkündür? Bu sualın cavabını riyaziyyatçılar verir.

Məsələ ondadır ki, məktəblilərin öyrəndikləri adi hesab əməliyyatlarıdır ibtidai məktəb, əslində, düşündüyümüz qədər bərabər deyil. Bütün sadə ədəd əməliyyatları ikiyə endirilə bilər: toplama və vurma. Bu hərəkətlər say anlayışının mahiyyətini təşkil edir və digər əməliyyatlar bu ikisinin istifadəsi üzərində qurulur.

Toplama və vurma

Standart çıxma nümunəsini götürək: 10-2=8. Məktəbdə bunu sadə hesab edirlər: on fəndən ikini çıxarsan, səkkiz qalır. Amma riyaziyyatçılar bu əməliyyata tamam başqa cür baxırlar. Axı, çıxma kimi əməliyyat onlar üçün mövcud deyil. Bu misal başqa cür də yazıla bilər: x+2=10. Riyaziyyatçılar üçün naməlum fərq sadəcə olaraq səkkiz etmək üçün ikiyə əlavə edilməli olan ədəddir. Və burada heç bir çıxma tələb olunmur, sadəcə olaraq müvafiq ədədi dəyəri tapmaq lazımdır.

Bölmə və vurma eyni şəkildə aparılır. 12:4=3 nümunəsində başa düşə bilərsiniz ki, söhbət səkkiz obyekti iki bərabər yığına bölməkdən gedir. Amma reallıqda bu, sadəcə olaraq 3x4 = 12 yazmaq üçün ters çevrilmiş bir düsturdur. Bölmə ilə bağlı belə nümunələri sonsuzca vermək olar.

0-a bölmək üçün nümunələr

Niyə sıfıra bölə bilməyəcəyiniz burada bir az aydın olur. Sıfıra vurma və bölmə öz qaydalarına uyğundur. Bu kəmiyyətin bölünməsinin bütün nümunələri 6:0 = x şəklində tərtib edilə bilər. Lakin bu, 6 * x=0 ifadəsinin tərsinə çevrilmiş qeydidir. Amma bildiyiniz kimi istənilən ədədi 0-a vurmaq hasildə yalnız 0 verir.Bu xassə elə sıfır dəyər anlayışına xasdır.

Belə çıxır ki, elə bir rəqəm yoxdur ki, 0-a vurulduqda hər hansı maddi dəyər versin, yəni bu məsələnin həlli yoxdur. Bu cavabdan qorxmamalısınız, bu tip problemlər üçün təbii cavabdır. Sadəcə, 6:0 hesabının heç bir mənası yoxdur və heç nəyi izah edə bilməz. Bir sözlə, bu ifadəni ölməz “sıfıra bölmək mümkün deyil” ifadəsi ilə izah etmək olar.

0:0 əməliyyatı varmı? Doğrudan da, 0-a vurma əməliyyatı qanunidirsə, sıfırı sıfıra bölmək olarmı? Axı 0x 5=0 formasında olan tənlik kifayət qədər qanunidir. 5 rəqəminin yerinə 0 qoya bilərsiniz, məhsul dəyişməyəcək.

Həqiqətən, 0x0=0. Ancaq yenə də 0-a bölmək olmaz. Qeyd edildiyi kimi, bölmə sadəcə vurmanın tərsidir. Beləliklə, misalda 0x5=0 olarsa, ikinci amili təyin etmək lazımdırsa, 0x0=5 alırıq. Və ya 10. Və ya sonsuzluq. Sonsuzluğu sıfıra bölmək - bunu necə bəyənirsiniz?

Ancaq hər hansı bir rəqəm ifadəyə uyğun gəlirsə, bunun mənası yoxdur, biz sonsuz sayda rəqəmlərdən yalnız birini seçə bilmərik. Əgər belədirsə, bu o deməkdir ki, 0:0 ifadəsinin mənası yoxdur. Belə çıxır ki, hətta sıfırın özü də sıfıra bölünə bilməz.

Ali riyaziyyat

Sıfıra bölmək orta məktəb riyaziyyatı üçün başağrısıdır. Texniki universitetlərdə öyrənilən riyazi analiz həlli olmayan problemlər anlayışını bir qədər də genişləndirir. Məsələn, artıq məşhur ifadə 0:0-da həlli olmayan yeniləri əlavə olunur məktəb kursları riyaziyyat:

• sonsuzluğun sonsuzluğa bölünməsi: ∞:∞;
• sonsuzluq mənfi sonsuzluq: ∞−∞;
• sonsuz gücə qaldırılmış vahid: 1 ∞ ;
• sonsuzluğun 0-a vurulması: ∞*0;
• bəzi başqaları.

Bu cür ifadələri elementar üsullarla həll etmək mümkün deyil. Amma ali riyaziyyat bir sıra oxşar nümunələr üçün əlavə imkanlar sayəsində son həllər verir. Bu, xüsusilə məhdudiyyətlər nəzəriyyəsindən problemlərin nəzərdən keçirilməsində özünü göstərir.

Qeyri-müəyyənliyin açılması

Limitlər nəzəriyyəsində 0 qiyməti şərti sonsuz kiçik dəyişənlə əvəz olunur. İstədiyiniz dəyəri əvəz edərkən sıfıra bölmənin alındığı ifadələr çevrilir. Aşağıda adi cəbri çevrilmələrdən istifadə edərək limiti genişləndirməyin standart nümunəsi verilmişdir:

Nümunədə gördüyünüz kimi, sadəcə olaraq kəsri azaltmaq onun dəyərini tamamilə rasional cavaba gətirib çıxarır.

Limitləri nəzərdən keçirərkən triqonometrik funksiyalar onların ifadələri ilk əlamətdar həddə qədər azalmağa meyllidir. Limit əvəz edildikdə məxrəcin 0-a çevrildiyi limitləri nəzərdən keçirərkən, ikinci əlamətdar hədd istifadə olunur.

L'Hopital metodu

Bəzi hallarda ifadələrin hədləri onların törəmələrinin hədləri ilə əvəz edilə bilər. Guillaume L'Hopital - Fransız riyaziyyatçısı, fransız məktəbinin banisi riyazi analiz. O, sübut etmişdir ki, ifadələrin hüdudları bu ifadələrin törəmələrinin hüdudlarına bərabərdir. Riyazi qeydlərdə onun qaydası belə görünür.

Əgər ədəd sonsuzluğa bölünürsə, hissə sıfıra meyl edəcəkmi? İçəridə davam etdi və ən yaxşı cavabı aldı

Olenkadan cavab[yeni]
hamısı 0
Krab Вark
Oracle
(56636)
Yox. Tam sıfır. Bölən sonsuzluğa meylli olduğu kimi, hissə də sıfıra meyl edəcəkdir. Və əgər sonsuzluğa meylli bir ədədə deyil, sonsuzluğun özünə bölünsək (yeri gəlmişkən, daha dəqiq desək, bu, rəsmi olaraq ümumiyyətlə nömrə hesab edilmir, ancaq nömrələrin təyinatını tamamlayan xüsusi simvol hesab olunur) - tam sıfır.

-dan cavab Iugeus Vladimir[quru]
Sıfırı bölsəniz də, istənilən ədədə vursanız belə, yenə də sıfır olacaq!

-dan cavab 1 23 [quru]
əgər hansısa cəfəngiyat sıfıra meyl edirsə, onda onu sonlu bir şeyə (ədəd və ya məhdud funksiya) vurmaq faydasızdır, çünki hər şey sıfıra meyllidir.
ancaq onu sonsuzluğa meyl edən bir növ şeylə çarparsanız, variantlar ola bilər.

-dan cavab Krab Вark[quru]
Hər hansı bir ədəd sonsuzluğa bölündükdə nəticə sıfırdır. Dəqiq sıfır, “sıfıra can atmaq” yoxdur. Və sonra onu hansı rəqəmə vursan da, sıfır. Sıfırın sıfırdan başqa hər hansı bir ədədə bölünməsinin nəticəsi sıfır olacaq, yalnız sıfırı sıfıra böldükdə nəticə müəyyən edilmir, çünki hər hansı bir ədəd bölmə kimi uyğun olacaq.

Limitlərin həlli üsulları. Qeyri-müəyyənliklər.
Funksiyanın böyümə qaydası. Əvəzetmə üsulu

Misal 4

Həddini tapın

Bu daha sadə bir nümunədir müstəqil qərar. Təklif olunan nümunədə yenə qeyri-müəyyənlik (daha çox yüksək sifariş kökdən hündürlük).

"x" "mənfi sonsuzluğa" meyllidirsə

Uzun müddətdir ki, bu məqalədə “mənfi sonsuzluq” xəyalı var. Çoxhədləri olan hədləri nəzərdən keçirək. Həll prinsipləri və üsulları bir sıra nüanslar istisna olmaqla, dərsin birinci hissəsində olduğu kimi tamamilə eyni olacaq.

Praktik tapşırıqları həll etmək üçün tələb olunacaq 4 hiyləyə baxaq:

1) Limiti hesablayın

Limitin dəyəri yalnız müddətdən asılıdır, çünki o, ən yüksək artım sırasına malikdir. Əgər, onda modulunda sonsuz böyükdür mənfi rəqəm bərabər dərəcəyə, V bu halda– dördüncüdə “plus sonsuzluğa” bərabərdir: . Sabit ("iki") müsbət, Buna görə də:

2) Limiti hesablayın

Budur, yenə ali dərəcə hətta, Buna görə də: . Ancaq qarşısında bir "mənfi" var ( mənfi sabit –1), buna görə də:

3) Limiti hesablayın

Limit dəyəri yalnız ondan asılıdır. Məktəbdən xatırladığınız kimi, "mənfi" tək dərəcənin altından "atılır", yəni modulunda sonsuz böyükdür mənfi ədədi TƏK gücə çevirin"mənfi sonsuzluğa" bərabərdir, bu halda: .
Sabit (“dörd”) müsbət, deməkdir:

4) Limiti hesablayın

Kənddə birinci oğlan yenə var qəribə dərəcə, əlavə olaraq, qoynunda mənfi sabit, yəni: Beləliklə:
.

Misal 5

Həddini tapın

Yuxarıdakı məqamlardan istifadə edərək, burada qeyri-müəyyənliyin olduğu qənaətinə gəlirik. Paylayıcı və məxrəc eyni böyümə sırasına malikdir, yəni limitdə nəticə sonlu bir ədəd olacaqdır. Bütün qızartmaları ataraq cavabı öyrənək:

Həll mənasızdır:

Misal 6

Həddini tapın

Bu, özünüz həll etməyiniz üçün bir nümunədir. Tam həll və dərsin sonunda cavab.

Və indi, bəlkə də, ən incə hallar:

Misal 7

Həddini tapın

Aparıcı şərtləri nəzərə alaraq, burada qeyri-müəyyənliyin olduğu qənaətinə gəlirik. Numerator məxrəcdən daha yüksək artım sırasına malikdir, buna görə də dərhal limitin sonsuzluğa bərabər olduğunu söyləyə bilərik. Bəs hansı sonsuzluq, “artı” və ya “mənfi”? Texnika eynidir - gəlin say və məxrəcdəki xırda şeylərdən xilas olaq:

Qərar veririk:

Pay və məxrəci bölün

Misal 15

Həddini tapın

Bu, özünüz həll etməyiniz üçün bir nümunədir. Dərsin sonunda yekun dizaynın təxmini nümunəsi.

Dəyişənlərin dəyişdirilməsi mövzusunda daha bir neçə maraqlı nümunə:

Misal 16

Həddini tapın

Birliyi limitlə əvəz etdikdə qeyri-müəyyənlik əldə edilir. Dəyişənin dəyişdirilməsi artıq özünü təklif edir, lakin əvvəlcə düsturdan istifadə edərək tangensi çeviririk. Doğrudan da, bizə bir tangens nə üçün lazımdır?

Qeyd edək ki, buna görə də. Tamamilə aydın deyilsə, sinus dəyərlərinə baxın triqonometrik cədvəl . Beləliklə, biz dərhal çarpandan xilas oluruq, əlavə olaraq, daha çox tanış olan 0: 0 qeyri-müəyyənliyi əldə edirik. Limitimiz sıfıra meyl etsəydi, yaxşı olardı.

Əvəz edək:

Əgər, onda

Kosinusun altında "x" var, onu da "te" ilə ifadə etmək lazımdır.
Əvəzindən ifadə edirik: .

Həllini tamamlayırıq:

(1) Əvəzetməni həyata keçiririk

(2) Kosinusun altındakı mötərizələri açın.

(4) Təşkil etmək ilk gözəl hədd , payı və əks ədədi süni şəkildə çoxaldın.

Müstəqil həll üçün tapşırıq:

Misal 17

Həddini tapın

Tam həll və dərsin sonunda cavab.

Bunlar siniflərində sadə tapşırıqlar idi, praktikada hər şey daha pis ola bilər və əlavə olaraq azaldılması düsturları, müxtəlif istifadə etməlisiniz triqonometrik düsturlar , eləcə də digər fəndlər. Məqalədə Kompleks Limitlər Bir neçə real nümunəni təhlil etdim =)

Bayram ərəfəsində, nəhayət, başqa bir ümumi qeyri-müəyyənliklə vəziyyəti aydınlaşdıracağıq:

“Sonsuzluğun gücünə bir” qeyri-müəyyənliyin aradan qaldırılması

Bu qeyri-müəyyənlik "xidmət olunur" ikinci gözəl hədd , və həmin dərsin ikinci hissəsində biz əksər hallarda praktikada rast gəlinən standart həllər nümunələrinə ətraflı baxdıq. İndi eksponentlərlə şəkil tamamlanacaq, əlavə olaraq, dərsin yekun tapşırıqları "yanlış" hədlərə həsr olunacaq, burada 2-ci gözəl həddi tətbiq etmək lazım olduğu görünür, baxmayaraq ki, bu heç də düzgün deyil. hal.

2-ci əlamətdar hədd üçün iki işləyən düsturun dezavantajı ondan ibarətdir ki, arqument “plus sonsuzluğa” və ya sıfıra meyl etməlidir. Bəs arqument fərqli bir rəqəmə meyl edərsə nə etməli?

Köməyə universal bir düstur gəlir (bu, əslində ikinci əlamətdar həddin nəticəsidir):

Qeyri-müəyyənlik düsturla aradan qaldırıla bilər:

Haradasa mən artıq kvadrat mötərizələrin nə demək olduğunu izah etmişəm. Xüsusi bir şey yoxdur, mötərizələr sadəcə mötərizələrdir. Onlar adətən riyazi qeydləri daha aydın vurğulamaq üçün istifadə olunur.

Formulun əsas məqamlarını vurğulayaq:

1) Haqqındadır yalnız qeyri-müəyyənlik haqqında və başqa heç nə.

2) “x” arqumenti meyl göstərə bilər ixtiyari dəyər(və yalnız sıfıra və ya deyil), xüsusən də "mənfi sonsuzluğa" və ya hər kəs sonlu ədəd.

Bu düsturdan istifadə edərək dərsdəki bütün nümunələri həll edə bilərsiniz. Möhtəşəm Limitlər , 2-ci əlamətdar həddə aid olan. Məsələn, limiti hesablayaq:

Bu halda , və düstura görə:

Düzdür, bunu etməyi məsləhət görmürəm, ənənə hələ də tətbiq oluna bilsə, həllin "adi" dizaynından istifadə etməkdir. Lakin düsturdan istifadə edərək yoxlamaq çox rahatdır 2-ci əlamətdar həddə "klassik" nümunələr.

Funksiyanın törəməsi uzağa düşmür və L'Hopital qaydalarına gəldikdə, o, ilkin funksiyanın düşdüyü yerə tam olaraq düşür. Bu vəziyyət 0/0 və ya ∞/∞ formasının qeyri-müəyyənliklərini və hesablama zamanı yaranan bəzi digər qeyri-müəyyənlikləri aşkar etməyə kömək edir. limit iki sonsuz kiçik və ya sonsuz böyük funksiyanın əlaqəsi. Bu qaydadan istifadə edərək hesablama çox sadələşdirilmişdir (əslində iki qayda və onlara qeydlər):

Yuxarıdakı düsturdan göründüyü kimi, iki sonsuz kiçik və ya sonsuz böyük funksiyanın nisbət həddi hesablanarkən, iki funksiyanın nisbət həddi onların nisbət həddi ilə əvəz edilə bilər. törəmələri və bununla da müəyyən nəticə əldə etmək.

L'Hopital qaydalarının daha dəqiq formalaşdırılmasına keçək.

İki sonsuz kiçik kəmiyyətin həddi halı üçün L'Hopital qaydası. Qoy funksiyalar f(x) Və g(x a. Və elə məqamda a a funksiyanın törəməsi g(x) sıfır deyil ( g"(x a bir-birinə bərabərdir və sıfıra bərabərdir:

.

İki sonsuz böyük kəmiyyətin həddi halı üçün L'Hopital qaydası. Qoy funksiyalar f(x) Və g(x) nöqtənin bəzi qonşuluğunda törəmələri (yəni diferensiallaşan) var a. Və elə məqamda a onların törəmələri olmaya bilər. Üstəlik, məntəqənin yaxınlığında a funksiyanın törəməsi g(x) sıfır deyil ( g"(x)≠0) və bu funksiyaların hədləri x nöqtəsində funksiyanın qiymətinə meyllidir a bir-birinə bərabərdir və sonsuzluğa bərabərdir:

.

Onda bu funksiyaların nisbətinin həddi onların törəmələrinin nisbətinin həddinə bərabərdir:

Başqa sözlə, 0/0 və ya ∞/∞ formasının qeyri-müəyyənlikləri üçün iki funksiyanın nisbətinin həddi, əgər sonuncu mövcuddursa, onların törəmələrinin nisbətinin həddi ilə bərabərdir (sonlu, yəni müəyyən sayda və ya sonsuz, yəni sonsuzluğa bərabərdir).

Qeydlər.

1. L'Hopital qaydaları funksiyaları yerinə yetirdikdə də tətbiq edilir f(x) Və g(x) nə vaxt müəyyən edilmir x = a.

2. Əgər funksiyaların törəmələrinin nisbətinin həddi hesablanarkən f(x) Və g(x) biz yenidən 0/0 və ya ∞/∞ formasının qeyri-müəyyənliyinə gəlirik, onda L'Hôpital qaydaları təkrar-təkrar tətbiq edilməlidir (ən azı iki dəfə).

3. L'Hopital qaydaları (x) funksiyalarının arqumenti sonlu ədədə meyl etmədikdə də tətbiq edilir. a, və sonsuzluğa ( x → ∞).

Digər növ qeyri-müəyyənliklər də 0/0 və ∞/∞ tiplərinin qeyri-müəyyənliklərinə endirilə bilər.

“Sıfırın sıfıra bölünməsi” və “sonsuzluğun sonsuza bölünməsi” növlərinin qeyri-müəyyənliklərinin açıqlanması

Misal 1.

x=2 0/0 formasının qeyri-müəyyənliyinə gətirib çıxarır. Beləliklə, hər bir funksiyanın törəməsi alınır

Çoxhədlinin törəməsi sayda, məxrəcdə isə - mürəkkəb loqarifmik funksiyanın törəməsi. Son bərabərlik işarəsindən əvvəl, adi limit, X yerinə iki ilə əvəz edilməsi.

Misal 2. L'Hopital qaydasından istifadə edərək iki funksiyanın nisbətinin limitini hesablayın:

Həll. Əvəzetmə verilmiş funksiya dəyərlər x

Misal 3. L'Hopital qaydasından istifadə edərək iki funksiyanın nisbətinin limitini hesablayın:

Həll. Verilmiş funksiyaya dəyərin əvəz edilməsi x=0 0/0 formasının qeyri-müəyyənliyinə gətirib çıxarır. Buna görə də, funksiyaların pay və məxrəcdə törəmələrini hesablayırıq və alırıq:

Misal 4. Hesablayın

Həll. Verilmiş funksiyaya əlavə sonsuzluğa bərabər olan x dəyərini əvəz etmək ∞/∞ formasının qeyri-müəyyənliyinə gətirib çıxarır. Beləliklə, L'Hopital qaydasını tətbiq edirik:

Şərh. Birinci törəmələrin nisbət həddi 0 formasının qeyri-müəyyənliyi olduğundan, L'Hopital qaydasının iki dəfə tətbiq edilməli olduğu, yəni ikinci törəmələrin nisbəti həddinə çatmalı olduğu nümunələrə keçək. /0 və ya ∞/∞.

“Sıfırla sonsuzluq” formasının qeyri-müəyyənliklərinin aşkarlanması

Misal 12. Hesablayın

.

Həll. alırıq

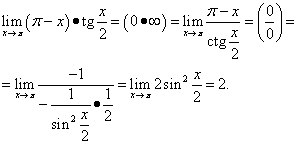
Bu nümunə triqonometrik eynilikdən istifadə edir.

“Sıfırdan sıfıra”, “Sıfırın gücünə sonsuzluq” və “sonsuzluğun gücünə bir” növlərinin qeyri-müəyyənliklərinin açıqlanması.

Formanın qeyri-müəyyənlikləri və ya adətən formanın funksiyasının loqarifmini götürərək 0/0 və ya ∞/∞ formasına endirilir.

İfadə limitini hesablamaq üçün xüsusi halı loqarifmin xassəsi olan loqarifmik eynilikdən istifadə etməlisiniz. .

Loqarifmik eynilikdən və funksiyanın davamlılıq xassəsindən istifadə edərək (həddinin işarəsindən kənara çıxmaq üçün) həddi aşağıdakı kimi hesablamaq lazımdır:

Ayrı-ayrılıqda eksponentdə ifadənin limitini tapmalı və qurmalısınız e tapılan dərəcəyə qədər.

Misal 13.

Həll. alırıq

.

.

Misal 14. L'Hopital qaydasından istifadə edərək hesablayın

Həll. alırıq

Eksponentdəki ifadənin limitini hesablayın

.

.

Misal 15. L'Hopital qaydasından istifadə edərək hesablayın