“Törəmələrin hesablanması” praktiki dərsi. “Törəmələrin hesablanması” praktiki dərsi y funksiyasının törəməsini tapın
Dərsin məqsədləri:
Maarifləndirici- diferensiasiya düsturlarını bilmək; fərqləndirmə qaydaları;
mürəkkəb funksiyanın diferensiallaşdırılması; törəmənin fiziki və həndəsi mənası;
funksiyanın qrafikinə toxunan tənliyi.
İnkişaf - funksiyaların törəmələrini tapa bilmək; fiziki mənadan, həndəsi mənadan istifadə etməklə məsələləri həll etmək; nöqtədə funksiyanın törəməsinin qiymətini tapın; yerinə yetirilən hərəkətləri riyazi cəhətdən düzgün izah edir və əsaslandırır.
Təhsil - müstəqillik, məsuliyyət, düşüncə tərbiyə etmək.
Dərslər zamanı
I. Təşkilati məqam.
II. Ev tapşırığını yoxlamaq
(tənəffüs zamanı məsləhətçilər (şagirdləri) yoxlayır və qiymətlər təyin edirlər).
III. Məqsəd təyini və motivasiya
Müəllim şagirdlərə bu dərsin “Törəmələrin hesablanması” mövzusunda yekun dərs olduğunu bildirir və onları öz məqsədlərini formalaşdırmağa dəvət edir.
Müəllim: “Böyük filosof Konfutsi bir dəfə demişdi: “Üç yol biliyə aparır: düşüncə yolu ən nəcib yol, təqlid yolu ən asan yol, təcrübə yolu isə ən acı yoldur”. Beləliklə, bu gün sinifdə hər biriniz bu mövzunu bilmək üçün hansı yolda olduğunu müəyyənləşdirəcəksiniz”.
Şagirdlərə törəmələrin hesablanması üzrə bilik və bacarıqlarını nümayiş etdirmək tapşırığı verilir və onlara dərs planı verilir.
Mərhələ I:“Yadda saxla” kartından istifadə edərək tapşırığı yerinə yetirmək.
(düsturlar və fərqləndirmə qaydaları haqqında biliklərin yoxlanılması).
Mərhələ II: Biliyin təkrarı və ümumiləşdirilməsi üzrə şifahi frontal iş.
III mərhələ:"Test proqnozu" (bu tapşırığı yerinə yetirərkən məsləhətçilərin köməyi məqbuldur).
IMərhələ V: Praktik problemin həlli.
Mərhələ V: Müstəqil iş
İşin I, III, V mərhələləri və ev tapşırıqları qiymətləndirilir. Məsləhətçilər nəticələri yoxlayır və qiymətləndirmə cədvəlinə daxil edirlər.
Qiymətləndirmə meyarı: "5"- 19-20 bal;
"4"- 15-18 bal;
"3"- 10-14 bal.
Biliyə aparan yollar
- İstinad biliklərinin bərpası və korreksiyası
Mərhələ I.
Hədəf: düsturlar və diferensiasiya qaydaları haqqında biliklərə nəzarət, özünə nəzarət
Unutma! F.İ. ______________________________________________________ |
|
törəmə |
|
c,c - mənfi cəhətlər t |
|
|
|
|
|
f"(x)+ g"(x) |
|
f(x)* g(x) |
|
|
|
Bu tapşırığın sonunda “Törəmələr Cədvəli”ndən istifadə etməklə özünü yoxlama aparılır. Kartlar yoxlama üçün məsləhətçilərə verilir (kartlarda düzəlişlərə icazə verilmir).
V. Biliklərin ümumiləşdirilməsi və sistemləşdirilməsi
Mərhələ II.
1. Şifahi frontal iş.
A. Bu vəziyyət üçün tapşırıq yaradın və həll edin.
![]()
1. t = 3 nöqtəsində funksiyanın törəməsinin qiymətini tapın. (Cavab: 21.)
2. t = 3 nöqtəsində funksiyanın qrafikinə toxunan üçün tənlik yaradın. (Cavab: y = 21x-45.).
3. Hərəkət qanunu düsturla verilmişdirsə, t=3c anında cismin sürətini və təcilini tapın. (Cavab: 21 m/s, 16 m/s²).
4. t = 3 nöqtəsində funksiyanın qrafikinə çəkilmiş tangensin bucaq əmsalını tapın (Cavab: 21.).
5. t = 3 nöqtəsində funksiyanın qrafikinə toxunanın meyl bucağının tangensini tapın və Ox oxunun tangensi ilə müsbət istiqaməti arasındakı bucağın növünü təyin edin. (Cavab: tgα, α bucağı kəskindir)
B. Funksiyaların törəmələrini tapın

2. III mərhələ“Sınaq proqnozu”


Bu tapşırığın sonunda yekun cavablar əsasında özünü yoxlama aparılır və testlər məsləhətçilərə təhvil verilir. (kartlarda düzəlişlərə icazə verilmir).
Cavablar:
1 seçim |
||||
Seçim 2 |
- Problemin həlli
IMərhələ V
Qabaqcıl səviyyəli problemin frontal həlli (həlli siniflə birlikdə məsləhətçilər tərəfindən həyata keçirilir).
Tapşırıq
Hansı parametr dəyərlərində a funksiyanın qrafikinə tangenslər ![]()
onun X oxu ilə kəsişmə nöqtələrində çəkilmiş, öz aralarında 60° bucaq əmələ gətirir?

Qrafik, X oxunu iki nöqtədə kəsən yuxarı budaqları olan paraboladır (iş a=0 məsələnin mənasını təmin etmir):
IX. Ümumiləşdirmə və qiymətləndirmə
1. Suallar: a) Dərsin məqsədinə nail olundumu?
b) Hansı mərhələ ən çətin görünürdü?
c) Ən maraqlısı nə idi?
2. Məsləhətçilər nəticələri elan edirlər (yolda olan tələbələrin sayı və adları
təqlid, əks etdirmə yolları və təcrübə yolları).
Praktik iş
riyaziyyat
1. Funksiyanın limitinin tapılması. Birinci və ikinci gözəl məhdudiyyətlərdir.
2. Mürəkkəb funksiyanın törəməsi. Bir dəyişənin funksiyasının öyrənilməsi və qrafiklərin çəkilməsi.
3. Test “Funksiyaların öyrənilməsində diferensial hesablamanın tətbiqi”.
4. Qeyri-müəyyən inteqralların tapılması. Müəyyən inteqralların hesablanması.
5. Determinantların hesablanması.
6. Kramer üsulu ilə xətti tənliklər sistemlərinin həlli. Test.
7. “Çoxluqlar” mövzusunda məsələlərin həlli. Məntiq cəbr düsturları.
8. Təsadüfi hadisələrin ehtimallarının hesablanması. Ümumi ehtimal düsturu.
9. Ədədi xarakteristikaların hesablanması.
10. “Ehtimal nəzəriyyəsinin və riyazi statistikanın əsasları” testi
11. Kompleks ədədin triqonometrik forması.
12. Mürəkkəb ədədlərlə müxtəlif formalarda hərəkətlər.
RİYAZİYYAT FANINDAN PRAKTİKİ İŞ ÜÇÜN METODOLOJİ TƏLİMATLAR
KURS 2
Praktiki məşğələ tələbələrin tapşırığı əsasında və müəllimin rəhbərliyi altında bir və ya bir neçə praktiki işi yerinə yetirməsini nəzərdə tutan tədris prosesinin təşkili formasıdır.
Belə ki, riyaziyyatdan praktik məşğələlərdə şagirdlərdə gələcəkdə xüsusi fənlər üzrə peşəkar məsələlərin həllində istifadə edilməli olan məsələləri həll etmək bacarığı formalaşır.
Praktik iş zamanı tələbələr informasiya mənbələrindən istifadə etmək, normativ sənədlər və təlimat materialları, arayış kitabları ilə işləmək, çertyojlar, diaqramlar, cədvəllər tərtib etmək, müxtəlif növ məsələləri həll etmək, hesablamalar aparmaq bacarığına yiyələnirlər.
Riyaziyyatdan praktiki dərslər zamanı həll olunan məsələlər:
1) mühazirələr zamanı əldə edilmiş riyaziyyat üzrə nəzəri biliklərin genişləndirilməsi və möhkəmləndirilməsi;
2) şagirdlərdə riyaziyyatda problemlərin uğurla həll edilməsi üçün zəruri olan praktiki bacarıq və bacarıqların formalaşdırılması;
3) riyaziyyatın öyrənilməsi prosesində tələbələrin özünütəhsil və bilik və bacarıqlarının təkmilləşdirilməsinə ehtiyacın inkişafı;
4) riyaziyyatın öyrənilməsi prosesində yaradıcı münasibətin və tədqiqatçı yanaşmanın formalaşdırılması;
5) gələcək mütəxəssisin peşəkar əhəmiyyətli keyfiyyətlərinin və əldə edilmiş biliklərin peşəkar sahədə tətbiqi bacarıqlarının formalaşdırılması.
Praktiki dərs №1. Funksiya limitlərinin hesablanması. Birinci və ikinci gözəl məhdudiyyətlərdir.
Mövzu : Funksiya limitlərinin hesablanması.
Hədəf: riyaziyyatın fundamental sahələri sahəsində əsas biliklərə yiyələnmək . Funksiyaların hədlərinin hesablanması üzrə biliklərin mənimsənilməsinin yoxlanılması. Bu mövzuda bilikləri təkrarlayın və sistemləşdirin.
Tapşırıqlar:
Yaradıcı peşəkar təfəkkürün inkişafı;
Elm dilini mənimsəmək, əməliyyat anlayışları bacarıqları;
Problemlərin qoyulması və həlli bacarıqlarının mənimsənilməsi;
Nəzəri və praktiki hazırlığın dərinləşdirilməsi;
Tələbələrin təşəbbüskarlığının və müstəqilliyinin inkişafı.
Hesablama bacarıqlarının gücləndirilməsi;
Riyazi nitq üzərində işləməyə davam edin.
Müstəqil işləmək, dərsliklə işləmək, müstəqil bilik əldə etmək bacarıqlarının formalaşdırılması;
Mətnlə işləyərkən əsas şeyi vurğulamaq bacarığının inkişafı;
Müstəqil düşüncənin, zehni əməliyyatların formalaşması: müqayisə, təhlil, sintez, ümumiləşdirmə, analogiya;
Şagirdlərə tapşırıqların yerinə yetirilməsi mədəniyyəti üzrə biliklərin dərinləşdirilməsi və gücünün artırılması üçün sistemli işin rolunu göstərmək;
Şagirdlərin yaradıcılıq qabiliyyətlərinin inkişafı.
Praktik işin təmin edilməsi:
Praktiki iş üçün metodiki tövsiyələrin nəzəri materialı.
Riyaziyyat, – Seriya: Orta peşə təhsili. - Rostov-na-Donu “Feniks”, səh.
Praktik dərsin gedişi.
1.Dərsin mövzusunun formalaşdırılması, mövzunun akademik fənnin digər mövzuları ilə əlaqəsinin izahı;
2.Şagirdlərin dərsə hazırlığının yoxlanılması;
3. Mövzuya uyğun və fənnin iş proqramına uyğun olaraq faktiki dərsin keçirilməsi:
“Funksiyaların hədlərinin hesablanması” mövzusunda nəzəri materialı öyrənin.
Tipik tapşırıqların həlli nümunələrini nəzərdən keçirin.
Birinci və ikinci əlamətdar hədlərdən istifadə edərək funksiyaların hədlərinin hesablanması üzrə müstəqil iş aparın.
Təhlükəsizlik suallarını cavablandırın.
Nəzəri məlumat və metodoloji tövsiyələr
problemin həlli üzrə.
1. Nəzəri materialın təqdimatı.
Bir nöqtədə funksiyanın limitini hesablamaq üçün sizə lazımdır:
1) x dəyişəninin yerinə x-in nəyə meyl etdiyini əvəz edin.
2) Əgər 1-ci addımı tamamladıqdan sonra https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">formasında qeyri-müəyyənlik əldə ediriksə və dəyişdirin. mənfi olan ox: (x-a).
3) Əgər 1-ci addımı tamamladıqdan sonra https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> formasının qeyri-müəyyənliyini alırıqsa. triqonometrik funksiyaların dəyərləri ilə əlaqəli , ilk diqqətəlayiq həddi istifadə etməliyik.
Tərif.İlk diqqətəlayiq hədd hədd adlanır
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Tərif:İkinci əlamətdar hədd hədd adlanır

Bu həddlə verilən rəqəm həm riyazi analizdə, həm də riyaziyyatın digər sahələrində çox mühüm rol oynayır. Nömrə çağırılır təbii loqarifmlərin əsası ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Öyrənilən materialın konsolidasiyası.
Misal 1
https://pandia.ru/text/78/405/images/image015_1.png" eni="28" hündürlük="30 src=">= -4
Biz qayda 1) istifadə etdik və x yerinə x-in nəyə çalışmalı olduğunu, yəni x=2-ni əvəz etdik.
Misal 2
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
Misal 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" eni="138" hündürlük="24 src=">=3+3=6
Misal 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" hündürlüyü="30 src=">
Misal 5
https://pandia.ru/text/78/405/images/image032_0.png" eni="61" hündürlük="46 src=">.png" hündürlüyü="30 src=">=2
Misal 6
https://pandia.ru/text/78/405/images/image036_0.png" eni="18" hündürlük="28 src=">
b) 
V) 
3. Bilik, bacarıq və bacarıqların konsolidasiyası.
Funksiyaların hədlərinin hesablanması üzrə müstəqil iş görmək.
Praktiki iş №1. Seçim 1 Funksiya limitini hesablayın: 1. 2. 3. 10. | Praktiki iş №1. Seçim 2 Funksiya limitini hesablayın: 1. 2. 3. 10. |
Praktiki iş № 2.
Mövzu : Funksiyanın törəməsinin tapılması. Bir dəyişənin funksiyasının öyrənilməsi və qrafikin qurulması.
Hədəf : Funksiyanın törəməsi anlayışı, elementar funksiyaların törəmələrini, mürəkkəb funksiyaları, tərs funksiyaları tapmaq, törəmələr cədvəlindən və diferensiallaşma qaydalarından istifadə etmək bacarığını, mürəkkəb və tərs funksiya anlayışını, bacarığını praktikada yoxlamaq. funksiyaları öyrənmək üçün törəmədən istifadə etmək.
Praktik işin təmin edilməsi:
Dərs kitabı. "Riyaziyyat". – M.: Bustard, 2010.
Riyaziyyat. M: Forum-İnfa 2008.
Praktik iş seçimi ilə fərdi kartlar.
1. Funksiyanın törəməsinin tapılmasına dair nəzəri material və nümunələr.
Tərif: f(x) (f"(x)) funksiyasının x nöqtəsində törəməsi, arqumentin artımı sıfıra meyl etdikdə funksiyanın artımının arqumentin artımına nisbətinin həddidir:
https://pandia.ru/text/78/405/images/image061_0.png" eni="209 hündürlük=235" hündürlük="235">
Fərqləndirmə qaydaları.
Əgər f(x) və g(x) funksiyalarının törəmələri varsa, onda
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, burada C=const
5..png" eni="49" hündürlük="54 src=">
6. Kompleks funksiyanın törəməsi:
f′(g(x))=f′(g) g′(x)
2. Nümunələr.
1..png" eni="61" hündürlük="41 src=">.png" eni="20" hündürlük="41 src=">.png" eni="20" hündürlük="41 src="> .png" eni="69" hündürlük="41 src=">+4).
Funksiya iki amilin məhsuludur: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width="" 64" hündürlük="41 src=">.png" eni="19" hündürlük="41 src=">.png" eni="45" hündürlük="51 src=">.
Funksiya iki ifadənin bölünməsidir: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " hündürlük="57 src=">.png" eni="197 hündürlük=36" hündürlük="36">
Həll. Mürəkkəb funksiyaların diferensiasiya qaydasından istifadə edərək bu funksiyanın törəməsini tapaq (formula 6):

5. Əgər , onda 
6. y = x 3 – 3x 2 + 5x+ 2. Gəlin tapaq y "(–1).
y " = 3x 2 – 6x+ 5. Buna görə də, y "(–1) = 14.
7. Əgər y= log x cos x, Bu y" = (ln x)"çünki x+ln x(cos x) " =1/x∙cos x–ln x günah x.
Bir funksiya verilsin. Onu öyrənmək üçün sizə lazımdır:
1) Onun tərif sahəsini tapın. Çox çətin deyilsə, aralığı tapmaq da faydalıdır. (Lakin bir çox hallarda tapma məsələsi funksiyanın ekstremumları tapılana qədər təxirə salınır.)
2) Funksiyanın davranışını təyin etməyə kömək edəcək ümumi xassələrini tapın: funksiyanın cüt və ya tək olması, dövri olması.
3) Arqument təyin sahəsinin sərhəd nöqtələrinə yaxınlaşdıqda funksiyanın necə davrandığını öyrənin, əgər belə sərhəd nöqtələri varsa. Əgər funksiyanın kəsilmə nöqtələri varsa, bu nöqtələr də funksiyanın şaquli asimptotlarının olub-olmaması üçün yoxlanılmalıdır. Əyri asimptotları tapın.
4) Qrafikin koordinat oxları ilə kəsişmə nöqtələrini tapın ki, bu da şərt altında funksiyanın qiymətinin sadəcə hesablanmasından ibarətdir:
OX oxu ilə: y=0;
OY oxu ilə: x=0.
Oxla kəsişmə nöqtələrinin tapılması mürəkkəb cəbr tənliyini həll etmək ehtiyacına səbəb ola bilər ki, bu da, bəlkə də, yalnız təxminən edilə bilər. Funksiyanın köklərini və kəsilmə nöqtələrini tapdıqdan sonra bu nöqtələr arasındakı intervalların hər birində funksiyanın işarəsini təyin edə bilərik. Bu, ya intervalın istənilən nöqtəsində funksiyanın qiymətini hesablamaqla, ya da interval metodundan istifadə etməklə edilə bilər.
5) Monotonluq intervallarını tapın. Bunun üçün törəməni tapın və bərabərsizliyi həll edin:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, funksiya azalır.
Monotonluq intervallarını tapdıqdan sonra dərhal yerli ekstremum nöqtələrini təyin edə bilərik: artım azalma ilə əvəz olunduqda yerli maksimumlar, azalmanın artımla əvəz edildiyi yerlərdə isə yerli minimumlar yerləşir.
6) Qabarıqlıq və qabarıqlıq intervallarının tapılması ikinci törəmədən istifadə etməklə həyata keçirilir..png" width="39" height="19 src="> intervallar üzrə:
əgər https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, onda funksiya qrafiki əyrisi qabarıqdır.
Eyni zamanda, biz əyilmə nöqtələrini funksiyanın qabarıqlıq istiqamətini dəyişdirdiyi (və davamlı olduğu) nöqtələr kimi müəyyən edirik.
7) Qrafikin asimptotla və əlavə nöqtələrlə kəsişmə nöqtələrinin tapılması. Bu nöqtə məcburi deyil, lakin belə nöqtələrin tapılması funksiyanın və onun qrafikinin öyrənilməsini tam və tam edir.
Qeyd edək ki, çertyojda funksiyaların öyrənilməsi zamanı alınan nöqtələri dərhal koordinat oxları və qrafik üzərində çəkmək faydalıdır. Bu, yol boyu qrafikin görünüşünü başa düşməyə kömək edir.
3. Bunu özünüz edin:
|
seçim | y funksiyasının törəməsini tapın: |
seçim | y funksiyasının törəməsini tapın: |
1.y=6- | 1. y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Praktik dərs
Mövzu: Törəmələrin tapılması. Törəmənin funksiyaların öyrənilməsində və qrafiklərin qurulmasında tətbiqi.
Hədəf: Törəmələrin hesablanmasını mənimsəmək, törəmədən istifadə edərək funksiyanı araşdırmağı öyrənmək
Təhsil vasitələri: praktik məşğələlər üçün dəftərlər, mövzu üzrə təqdimatlar, internet resursları.
1. “Törəmələrin hesablanması qaydaları”, “Funksiyanın ekstremumu”, “Qabarıqlıq, qabarıqlıq” mövzuları üzrə nəzəri materialı nəzərdən keçirin. Bükülmə nöqtəsi."
2. Tapşırıqların nümunələrini nəzərdən keçirin.
3. 1 nömrəli test tapşırığını yerinə yetirin.
Nəzarət sualları:
1. Bir nöqtədə funksiyanın maksimumunu (minimumunu) təyin edin. Maksimum (minimum) nöqtənin kifayət qədər kiçik qonşuluğunda funksiyanın artımının işarəsi haqqında nə demək olar?
2. Funksiyanın ekstremumunun mövcud olması üçün zəruri şərtlər hansılardır? Onların həndəsi mənası nədir?
3. Seqmentdə funksiyanın ən böyük və ən kiçik qiymətlərinin tapılması qaydası hansıdır?
4. İnterval üzrə əyrinin qabarıqlığını (konkavliyini) təyin edin.
5. Əyrinin qabarıqlıq və qabarıqlıq intervallarının tapılması qaydası hansıdır?
6. Əyrinin əyilmə nöqtəsi. Onu necə tapmaq olar?
7. Funksiya qrafikinin qurulması alqoritmi hansıdır?
Törəmələrin hesablanması qaydaları
Mürəkkəb funksiyanın törəməsi.
Əgər saat=ƒ( Və), u=φ(x), onda saat¢ ( X)=ƒ¢ (i)·φ¢ (X).
Cəmin törəməsi.
Əgər saat(X)=Və(X)+v (X), Yəni saat¢ (X)=Və¢ (X)+v ¢ (X)
Məhsulun törəməsi.
Əgər y(x)=u(X)· v (X), Yəni saat¢ = Və¢ · v + u · v ¢ .
Xüsusilə, ( ilə· Və)¢ =c· Və¢, yəni törəmə işarəsinin altından daimi amil çıxarılır. Bunu yoxlamaq asandır
(u 2 ) ¢ = 2 u·u ¢ , (u 3 ) ¢ =3u 2 u ¢ , … , (u n ) ¢ =n·u n–1 u ¢ .
Hissənin törəməsi.
Əgər, onda  .
.
Törəmələr cədvəli
1. (ilə)¢ =0
Mürəkkəb funksiya üçün: əgər u=u(x), Bu:
2. (X)¢ =1
3. (X α )¢ = α · Xα–1, A- istənilən real rəqəm.
 .
.
3. 
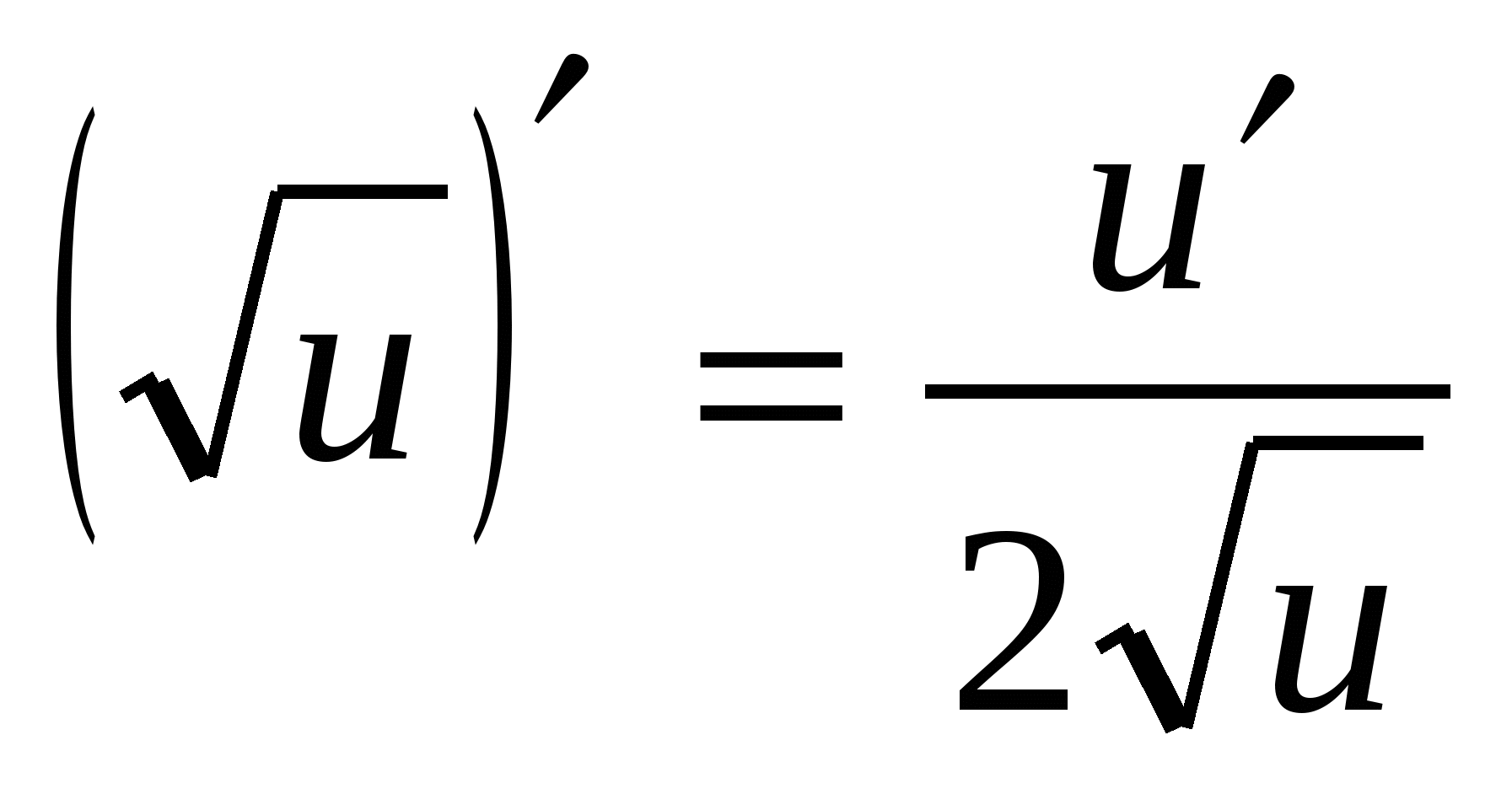
4. (A X ) ¢ =a X · ln A
4. 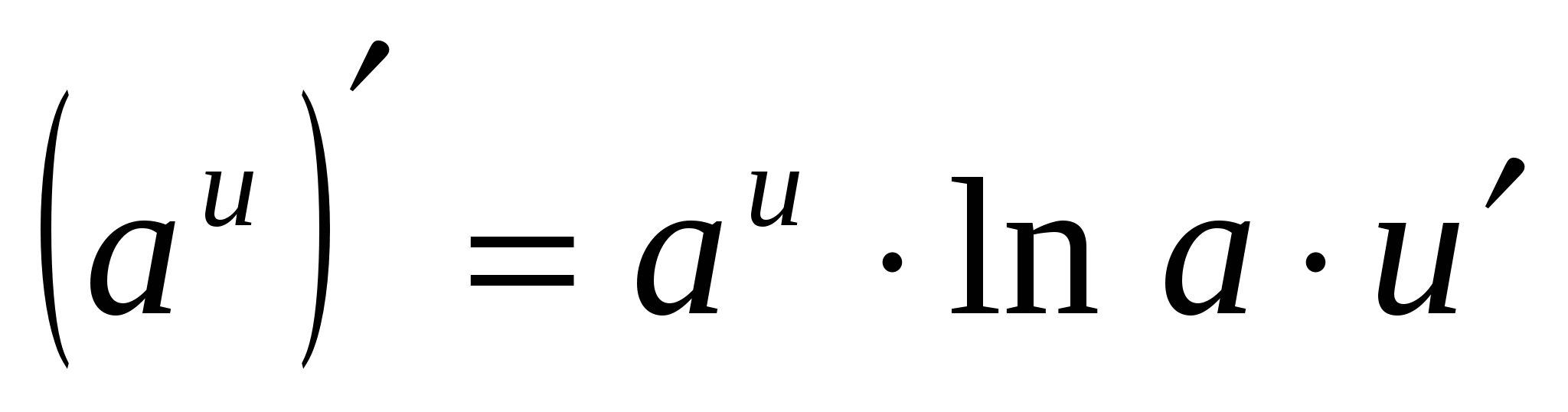
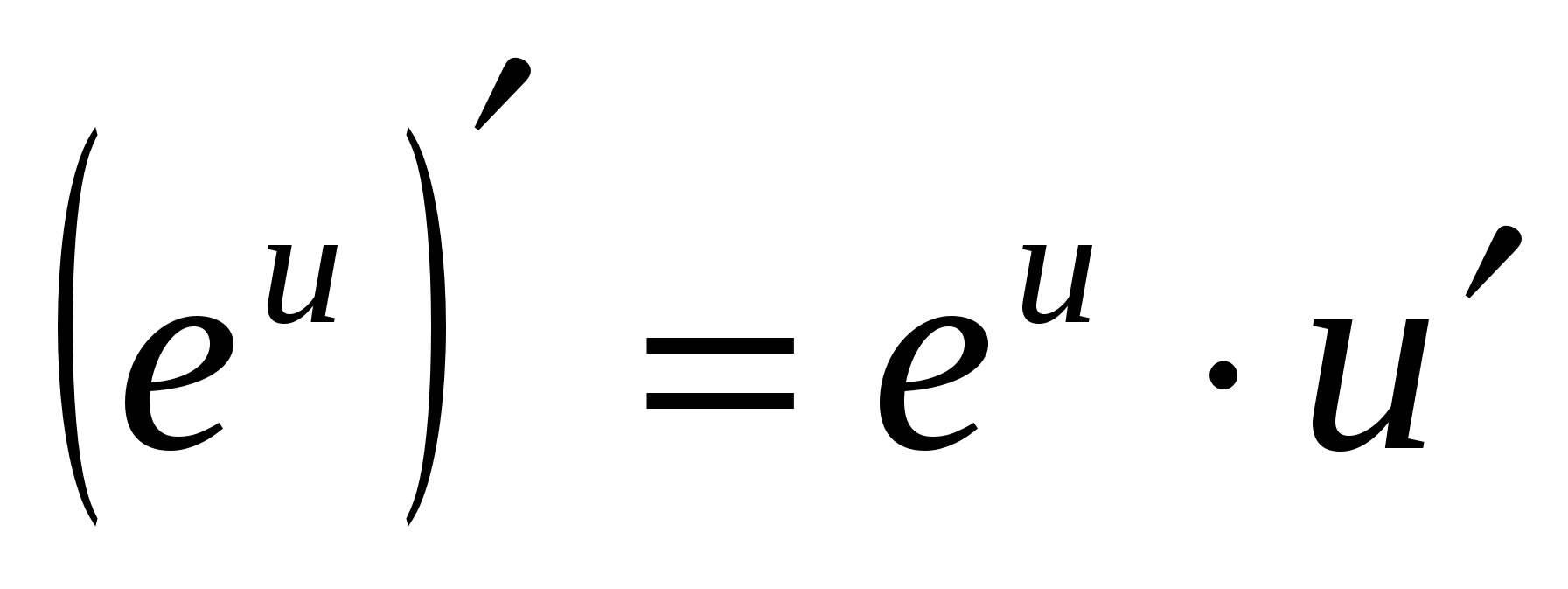
5. (log
a
x)
¢
=
 .
.
5. 

6. (günah x)¢ = cos x
6. 
7. (çünki x)¢ = –sin x
7. 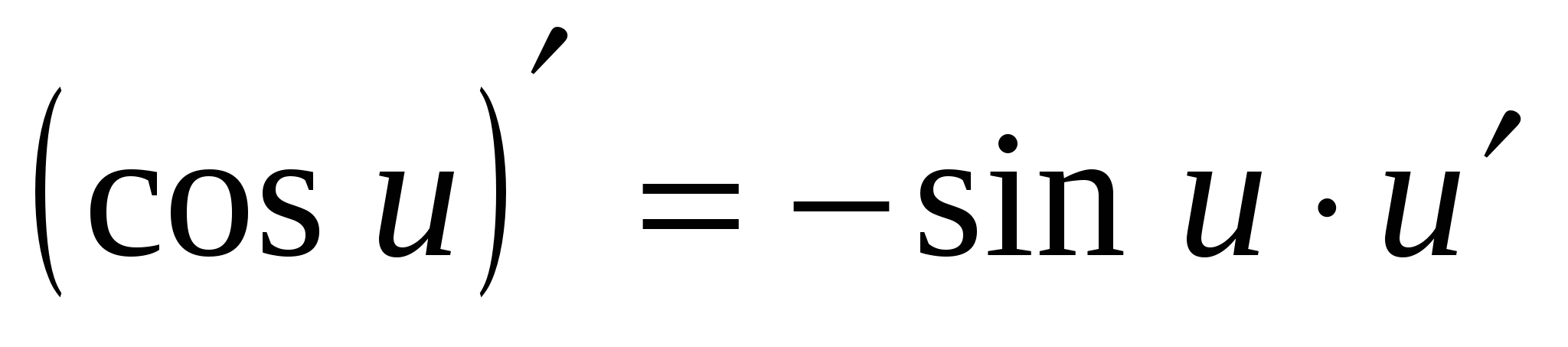
8. (tg x)¢
=
8. 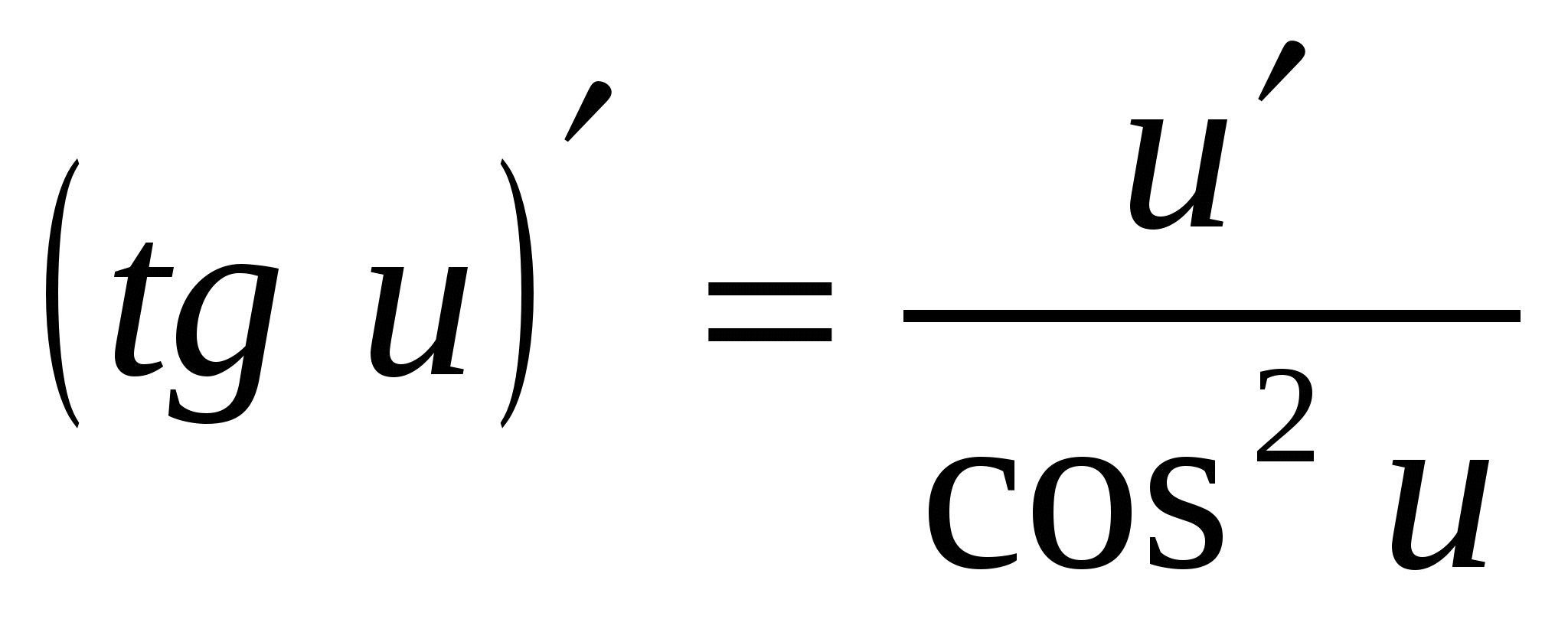
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 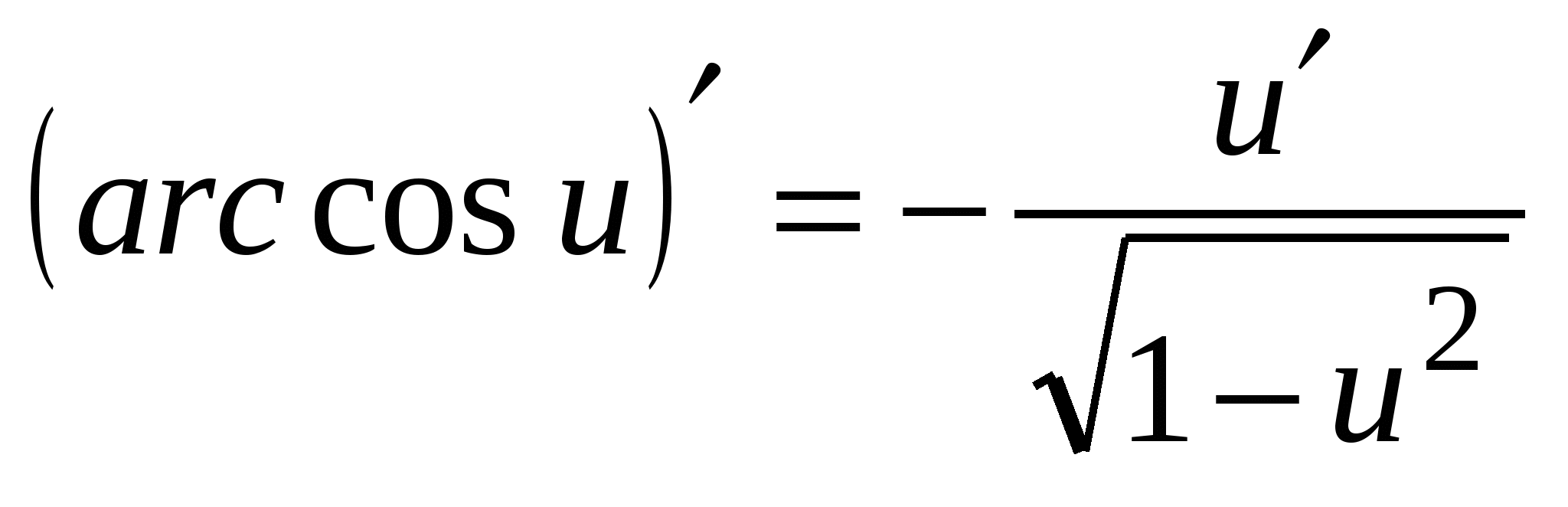
12. 
12. 
13. 
13. 
Nümunələri nəzərdən keçirin
Misal 1.
y=(3–2 günah 5x ) 4 | üçün törəmə düsturlar tətbiq edirik Və α ,günah u |
y ¢ =4·(3–2·sin5x) 3·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
Misal 2.
. 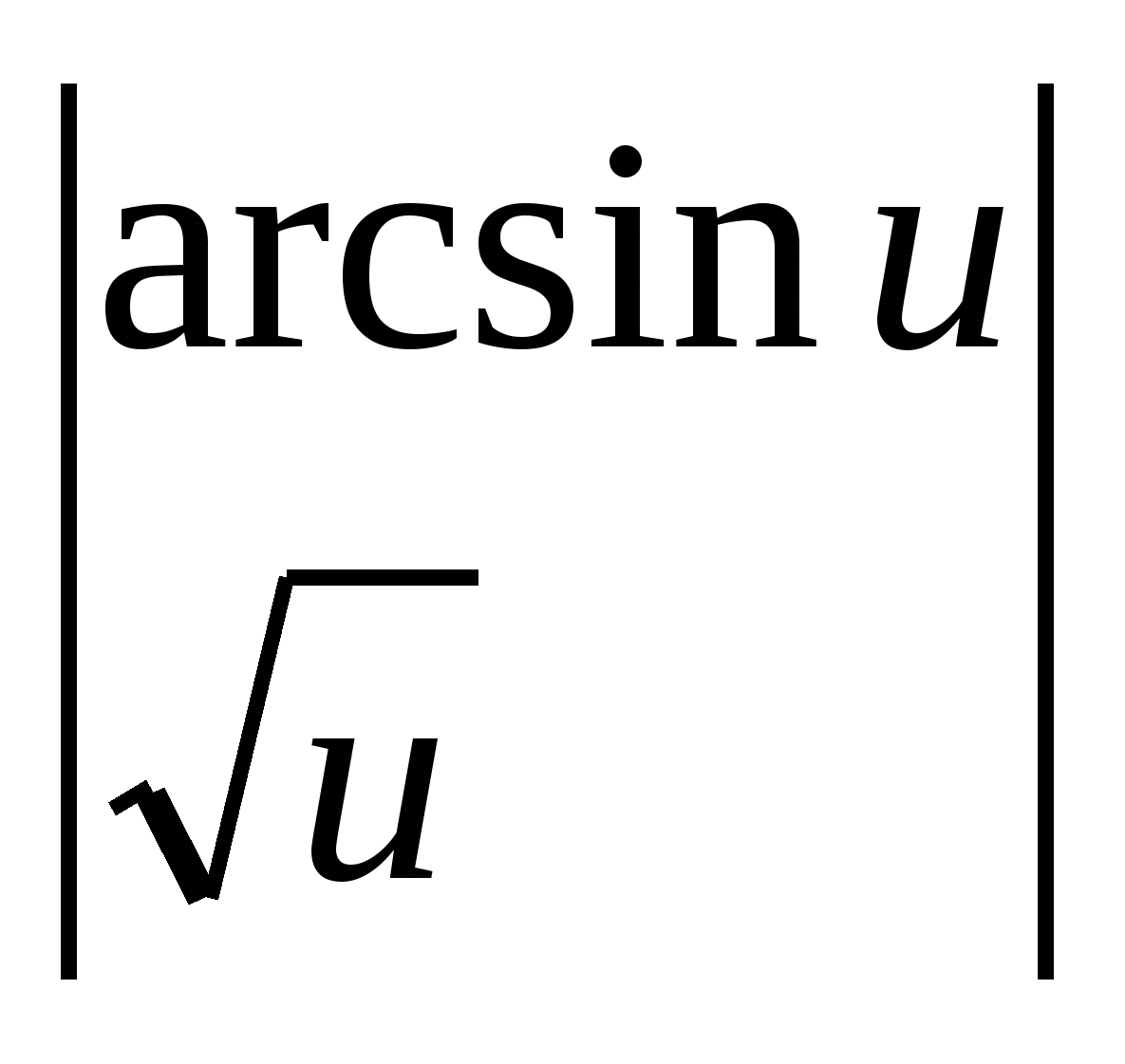

Misal 3.
 .
. 

Misal 4.



Misal 5.
 .
. 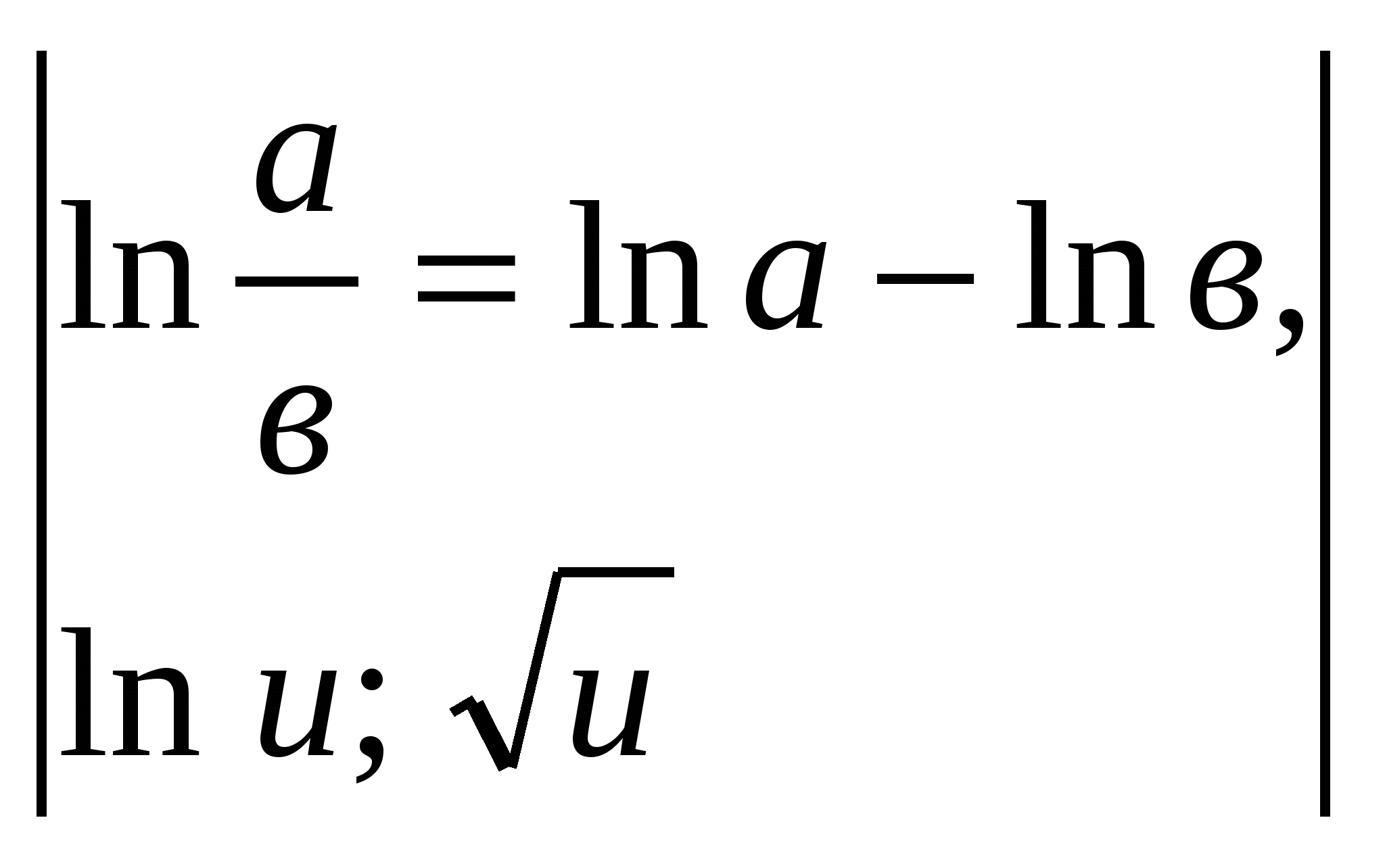

Funksiyanın ekstremumu
Ekstremumdakı funksiyanın tədqiqi törəmələrin ən vacib tətbiqlərindən biridir. Minimum və maksimalların tərifinə və onları necə tapacağına baxaq.
ƒ( funksiyası olsun X) müəyyən çoxluq və nöqtədə müəyyən edilir və diferensiallanır X 0 onun içindəki nöqtədir.
Tərif. Funksiya ƒ (X) nöqtəsində X 0 var maksimum(minimum), əgər nöqtənin belə bir qonşuluğu varsa X 0, hər kəs üçündür X bu ərazidən ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Nöqtə X 0 sonra nöqtə adlanır maksimum(minimum).

düyü. 1.
İki maksimum nöqtəsi olan funksiyanın qrafiki göstərilir ( X 1 və X 3) və iki minimum xal ( X 2 və X 4) və maksimum dəyər minimumdan az ola bilər ( ƒ (X 1 ) < ƒ (X 4)). Bu, bir funksiyanın təkliyini yalnız müəyyən bir nöqtənin yaxınlığında xarakterizə etdiyimizi vurğulayır.
Funksiyanın maksimum və minimum nöqtələrindəki qiymətlərinə ekstremal dəyərlər deyilir ifrat. Yuxarıdakı qrafik göstərir ki, ekstremal nöqtələr ( X 1 , X 2 , X 3 , X 4) hər birində törəmə müəyyən işarəni saxlayan funksiyanın monotonluq intervallarını təyin edin. Ekstremal nöqtələrdə, təbii ki, törəmə sıfıra keçir. haqqında bir teoremi formalaşdıraq zəruri şərt ekstremumun mövcudluğu.
Teorem.Əgər funksiyası ƒ (X) nöqtəsində X 0 ekstremumuna malikdir, onda bu nöqtədə funksiyanın törəməsi sıfıra bərabərdir, yəni ƒ¢ ( X 0)=0.
Dərhal qeyd edək ki, bu şərt kifayət deyil, yəni əks ifadə həmişə doğru deyil. Bərabərlikdən ƒ ¢ ( X 0)= 0 mütləq nöqtədə o demək deyil X 0 bir ekstremum var.
Bu funksiya ilə bir nümunə ilə təsdiqlənir ƒ (X)=x 3 .
tapacağıq ƒ ¢ ( X)= 3X 2 . nöqtədə X=0 ƒ ¢ (0)=0 . Amma istədiyiniz qədər nöqtəyə yaxın X=0 tapacağıq X> 0, harada ƒ (X)=x 3 > 0, tapacağıq X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, hamı üçün X bir nöqtədə funksiya dəyəri X=0 ən böyük və ya ən kiçik olacaq. Buna görə də nöqtə X=0 ekstremal nöqtə deyil.
Başqa cür mübahisə etmək olar. törəmə ildən ƒ ¢ (x)=3x 2 , sonra funksiya ƒ(x)=x 3 istənilən real x üçün artır və heç bir ekstremal yoxdur.
Lazımi ekstremum şərtin ödənildiyi nöqtələr (ƒ ¢ (x)=0) adlandırılır tənqidi .
Aydındır ki, ƒ olan nöqtələrdə funksiyanın qrafikinə tangens ¢ (x)=0, x oxuna paralel Ox .
Kifayət qədər şərait ekstremum aşağıdakı teoremlərdə verilir.
Teorem 1.Əgər X 0 funksiyanın kritik nöqtəsidir və ondan keçərkən törəmə işarəni dəyişir X 0 ekstremum nöqtədir, yəni törəmə işarəni artıdan mənfiyə dəyişirsə, bu maksimum nöqtədir, işarəni mənfidən artıya dəyişirsə, minimum nöqtədir.
Nəzərə alın ki, törəmə işarəni dəyişməzsə, bir nöqtədə ekstremum yoxdur. Birinci törəmədən istifadə edərək ekstremumu öyrənmək qaydası məktəb kursundan məlumdur. Bəzən ikinci törəmədən istifadə edərək ekstremum üçün kifayət qədər şərt formalaşdırmaq daha rahatdır.
ƒ( funksiyası olsun X) bəzi sahədə iki dəfə diferensiallana bilir (yəni ƒ( X) var ƒ¢ ( X) Və ƒ ¢¢ ( X)).
Teorem 2.Əgər X 0 – funksiyanın kritik nöqtəsi ƒ(x) və ƒ ¢¢ (X 0 ) > 0 , Bu X 0 - minimum nöqtə, əgər ƒ ¢¢ (X 0 ) < 0, то X 0 - maksimum nöqtə.
İkinci törəmədən istifadə etməklə funksiyanın qrafikinin qabarıqlığı və ya qabarıqlığı müəyyən edilir.
qabarıqlıq, qabarıqlıq. Bükülmə nöqtəsi.
Əyri y=ƒ(X) adlanır qabarıq şəkildəci aşağıda onun hər hansı tangens
ƒ ¢¢ ( X) < 0.
Əyri y=ƒ(X) adlanır konkav əyrinin bütün nöqtələri yalan olarsa, intervalda daha yüksək onun hər hansı tangens bu intervalda. Sonra bu intervalda
ƒ ¢¢(x) > 0
Tərif. Bükülmə nöqtəsi əyri əyrinin bir tərəfi qabarıq, digər tərəfi isə konkav olduğu nöqtədir.
Bükülmə nöqtəsində ƒ ¢¢ ( X)=0.
Deməli, ikinci törəmənin işarəsi (həmçinin funksiyanın özünün və onun birinci törəməsinin işarəsi) funksiya qrafikinin xüsusiyyətlərini göstərir. Gəlin onlara yenidən baxaq.
Hər kəs üçün X interval üzrə ( A, b) ƒ (X) > 0 (ƒ (X) < 0), onda qrafik x oxunun üstündə (aşağıda) yerləşir.
Hər kəs üçün X interval üzrə ( A, b) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (A, b) artır (azalır).
Hər kəs üçün X interval üzrə ( A, b) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (A, b) qabarıq (qabarıq).
Tənlik ƒ( X)=0 funksiyanın “sıfırlarını”, yəni qrafikin Ox oxu ilə kəsişmə nöqtələrini təyin edir.
tənlik ƒ ¢ ( X)=0 kritik nöqtələri müəyyən edir.
tənlik ƒ ¢¢ ( X)=0 mümkün əyilmə nöqtələrini müəyyən edir.
Funksiyaların öyrənilməsi sxemi
Funksiyanı öyrənmək üçün ƒ (X) və hiylə qurmaq y=ƒ(X) tapılmalıdır:
1) funksiyanın təyini sahəsi və qrafikin koordinat oxları ilə kəsişmə nöqtəsi;
2) monotonluq intervalları;
3) ekstremal nöqtələr və bu nöqtələrdə funksiya qiymətləri;
4) qrafikin qabarıqlıq və qabarıqlıq intervalları;
5) qrafikin əyilmə nöqtələri;
6) bütün alınan nöqtələri (bəzən qrafiki aydınlaşdırmaq üçün əlavə nöqtələr alınır) və qrafikin özünü dekart koordinat sistemində qurun.
Bir seqmentdə funksiyanın ən kiçik və ən böyük dəyərləri
Optimallaşdırma metodunun bəzi problemlərini həll edərkən, müəyyən bir seqmentdə bir funksiyanın ən kiçik və ya ən böyük dəyərlərini tapa bilmək vacibdir. Funksiya bu dəyərlərə ya kritik nöqtələrdə, ya da seqmentin sonunda çatır.
Axtarış sxemi funksiyanın ən kiçik və ən böyük dəyərləri ƒ (X) seqmentdə [ A, b].
1. Funksiyanın törəməsini tapın ƒ ¢ ( X).
2. Tənlikdən kritik nöqtələri tapın ƒ ¢ ( X)=0.
3. Bu seqmentə aid olan kritik nöqtələri seçin [ A, b] və funksiyanın qiymətini tapın ƒ (X) hər belə nöqtədə.
4. Funksiya qiymətlərini hesablayın ƒ (X) seqmentin sonunda: ƒ( A) və ƒ( b).
5. Alınan funksiya qiymətlərindən ən böyüyü (ən böyük) və ən kiçiyi (ən kiçiyi) seçin.
Misal 2.
Funksiyanın ən böyük və ən kiçik qiymətlərini tapın ƒ(x)=X 3 -9x 2 +24х–10 seqmentdə.
1. ƒ ¢ ( X)= 3X 2 – 9·2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. x 2 =4 nöqtəsi seqmentə aid deyil. Buna görə də funksiyanın qiymətini yalnız nöqtədə hesablayırıq X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Seqmentin sonundakı funksiya qiymətləri: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Əldə edilən dəyərlər:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Ən yüksək dəyər 10-dur və nöqtəyə çatır X=2. Ən kiçik -10-a bərabərdir və nöqtədə əldə edilir X=0.
Misal 3.
Əyrinin qabarıqlıq və qabarıqlıq intervallarını və əyilmə nöqtələrini tapın y=x+36X 2 –2X 3 –X 4 .
Bu funksiyanın tərif sahəsi bütün həqiqi ədədlərin çoxluğudur, yəni. XЄ(–∞, +∞).
İkinci törəməni tapaq.
saat¢ =1+72 X–6X 2 –4X 3 .
saat¢¢ =72–12 X–12X 2 = –12(X 2 +X–6).
Eq. saat¢¢ =0 əyilmə nöqtəsinin absissini alırıq:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
İşarəni təyin edək saat¢¢ fasilələrlə
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
saat¢¢
əyri forması
qabarıq
əyilmə
konkav
əyilmə
qabarıq
Bükülmə nöqtələrinin ordinatlarını tapaq:
saat(–3)=726; M 1 (–3; 726) – əyilmə nöqtəsi
saat(2)=114; M 2 (2; 114) – əyilmə nöqtəsi.
(–3; 2) intervalında əyri konkav olur. (–∞; –3) və (2; +∞) intervallarında – qabarıq.
Tapşırıq nümunələri
Tapşırıq №1.
Funksiyanın kəsilmə nöqtələrini tapın və qrafiki qurun

Funksiya ƒ (X) bütün real üçün müəyyən edilir X və göstərilən intervalların hər birində davamlıdır: (–∞; –1), [–1; 0], (0, +∞). Gəlin funksiyanı araşdıraq ƒ (X) nöqtələrdə davamlılıq üçün X= –1 və X=0.
Bunun üçün bu nöqtələrin hər birində birtərəfli limitlər tapacağıq.

Birtərəfli məhdudiyyətlər fərqli olduğu üçün X = –1 – birinci növ kəsilmə nöqtəsi.
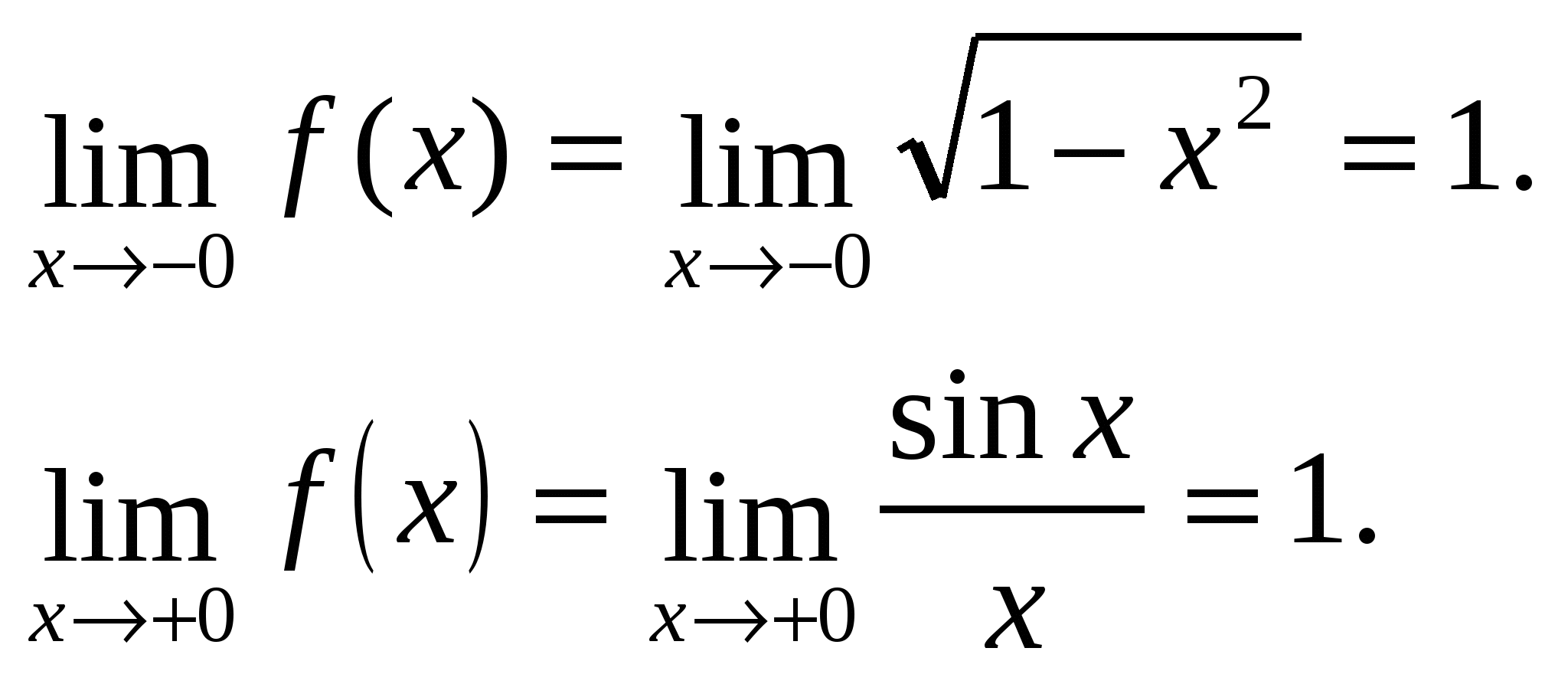
Birtərəfli hədlər bərabərdir, yəni x=0 nöqtəsində funksiyanın limiti var və 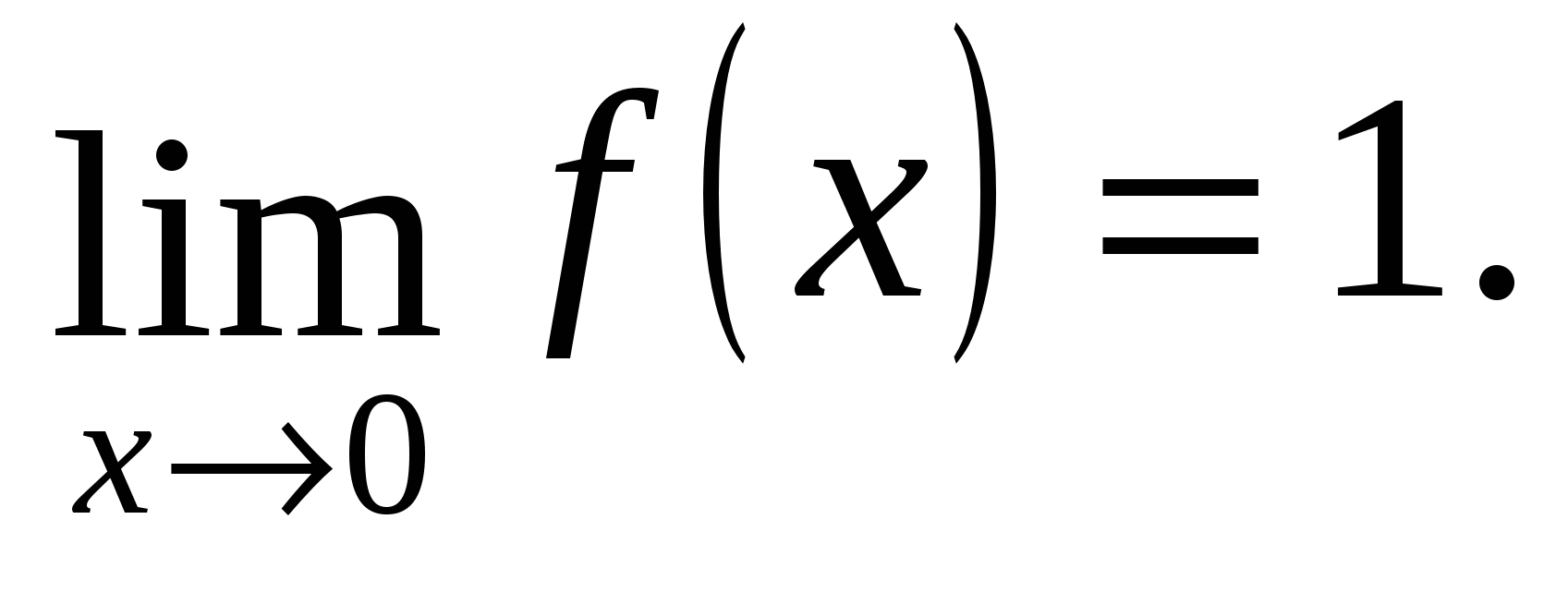
Bu limiti funksiyanın nöqtədəki qiyməti ilə müqayisə edək: 
Çünki  sonra daxil x=0-da ƒ(x) funksiyası davamlıdır.
sonra daxil x=0-da ƒ(x) funksiyası davamlıdır.
ƒ funksiyasının qrafikini çəkək (X), bunu nəzərə alaraq
1)  - düz xəttin tənliyi,
- düz xəttin tənliyi,
2)  – yuxarı yarımdairənin tənliyi
– yuxarı yarımdairənin tənliyi  mərkəzi başlanğıcda və radius vahidə bərabər olmaqla və şərtlə -1 £ X£ 0 tənliyi
mərkəzi başlanğıcda və radius vahidə bərabər olmaqla və şərtlə -1 £ X£ 0 tənliyi  dörddəbir dairəni müəyyən edir.
dörddəbir dairəni müəyyən edir.
3) üçün X > 0 qrafik tənliklə verilir  . Bu əyrinin Ox oxu ilə kəsişmə nöqtələrini tənlikdən tapırıq
. Bu əyrinin Ox oxu ilə kəsişmə nöqtələrini tənlikdən tapırıq 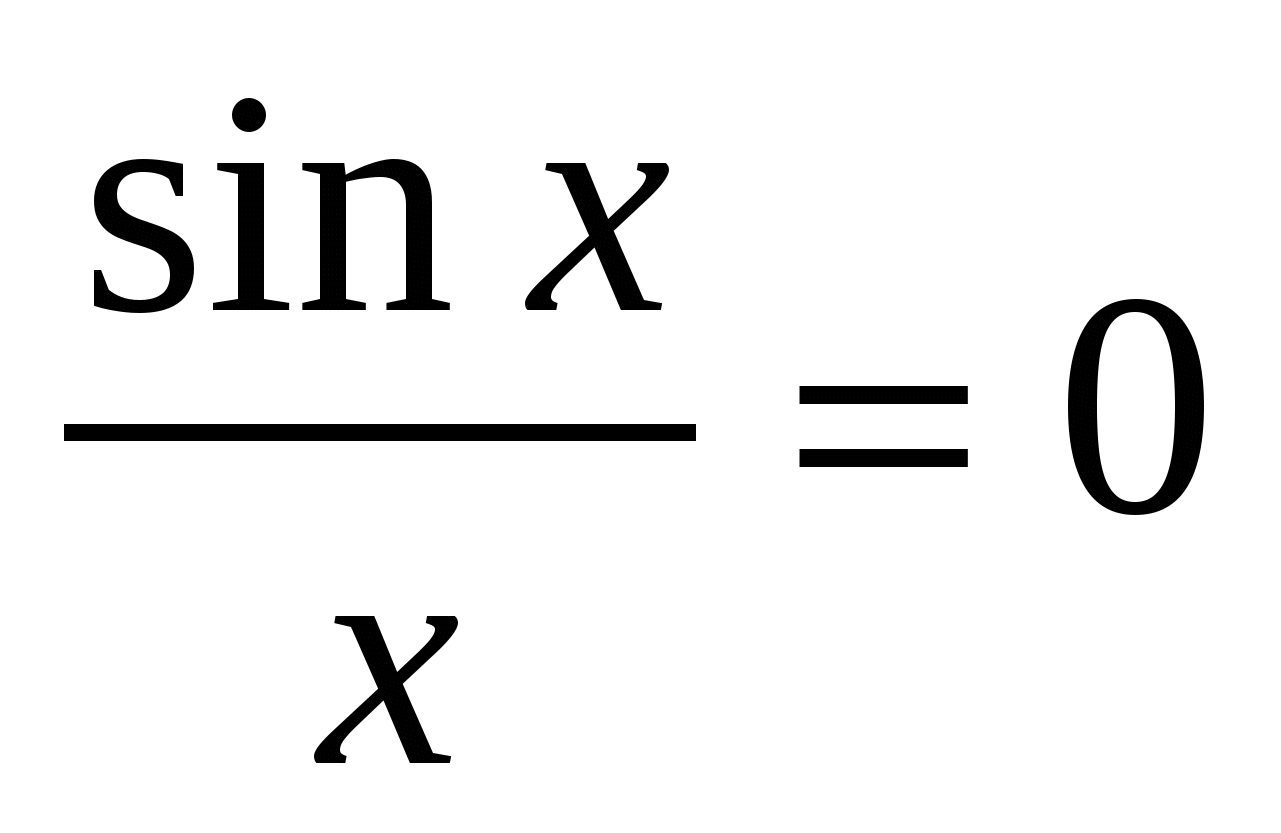 x > 0 üçün. x= π
n, Harada n
=1, 2, 3, 4,
x > 0 üçün. x= π
n, Harada n
=1, 2, 3, 4,

düyü. 2.
Tapşırıq № 2.
Xəttin tangensləri üçün tənlikləri yazın  olduğu nöqtələrdə X=0 və X=4. Tangenslərin kəsişmə nöqtəsini və aralarındakı bucağı tapın. Rəsm çəkin.
olduğu nöqtələrdə X=0 və X=4. Tangenslərin kəsişmə nöqtəsini və aralarındakı bucağı tapın. Rəsm çəkin.
Xəttə toxunan tənliyi y=ƒ(x) oxşayır
Harada saat 0 =ƒ( X 0).
nöqtədə X=0 saat(0)=ƒ(0)=5.
saat¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
M 1 (0, 5) formasına malikdir y– 5= –3(X–0) və ya
y= –3X+5.
nöqtədə X=4 saat(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Bir nöqtədə tangensin tənliyi M 2 (4, 1) formasına malikdir y– 1=X-4 və ya
y=x–3.
Sistemi həll etməklə tangenslərin kəsişmə nöqtəsini alırıq

Kəsişmə nöqtəsi M 3 (2, –1).
Künc φ düsturdan tangenslər arasında tapırıq:
 ,
,
Harada k 1 = –3; k 2 =1 – tangenslərin bucaq əmsalları.
 .
.
Künc φ =arctg 2.
Gəlin bu xətti quraq  – nöqtəsində təpəsi olan parabola X=3, çünki saat¢
= 0 X=3. tapacağıq
– nöqtəsində təpəsi olan parabola X=3, çünki saat¢
= 0 X=3. tapacağıq  . Nöqtə M 4 (3;
. Nöqtə M 4 (3;  ) parabolanın təpə nöqtəsidir.
) parabolanın təpə nöqtəsidir.
R 
edir. 3.
Tapşırıq №3.
Funksiyanı araşdırın 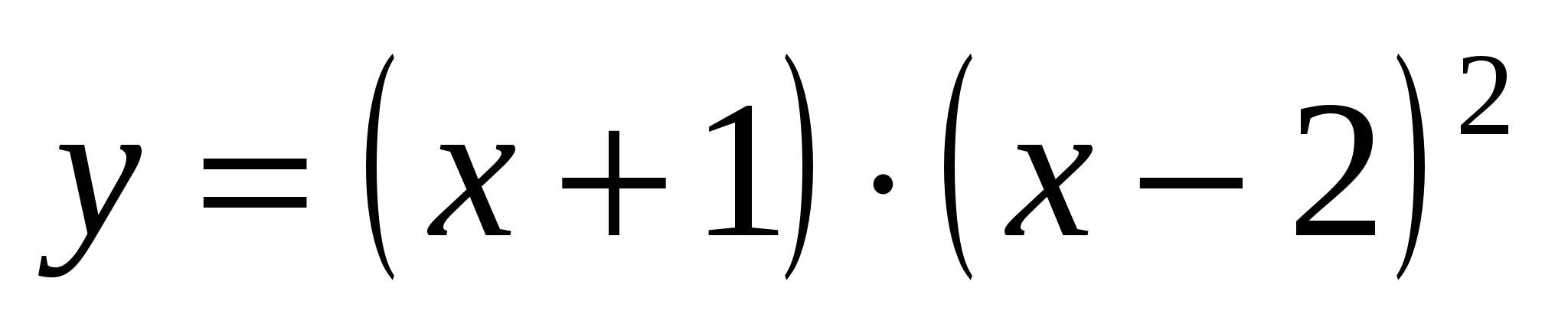 və onu tərtib edin.
və onu tərtib edin.
1. Bu funksiya çoxhədlidir (mötərizələri aça bilərsiniz, biz üçüncü dərəcəli çoxhədli alırıq), ona görə də hər hansı bir funksiya üçün müəyyən edilmiş, davamlı və diferensialdır. X.
2. Gəlin törəməni tapaq.
 .
.
Eq. saat¢ =0 kritik nöqtələri tapaq: 3 X·( X–2)=0, X 1 =0, X 2 =2.
Gəlin onları araşdıraq.
X
(–∞, 0)
(0; 2)
(2; +∞)
saat ¢
saat
3. Deməli, funksiya (–∞, 0) və (2, +∞) intervallarında artır, (0; 2) intervalında azalır, x=0-da maksimuma, x=2-də minimuma malikdir:
saat maksimum = saat(0)=4; saat min = saat(2)=0.
4. İkinci törəməni tapaq.
saat¢¢ = 6·( X-1).
Burada əyri qabarıqdır saat¢¢ < 0, т. е. 6·(X–1) < 0, X < 1.
Əyri olduğu yerdə içbükeydir saat¢¢ > 0, yəni. X > 1.
Beləliklə, (–∞, 1) intervalında əyri qabarıqdır; və (1, +∞) intervalında o, konkavdır.
5. Tənlikdən əyilmə nöqtəsini tapırıq saat¢¢ =0. Beləliklə, X=1 – əyilmə nöqtəsinin absisi, çünki bu nöqtə əyrinin qabarıqlıq və qabarıqlıq intervallarını ayırır. Bükülmə nöqtəsi ordinatı: saat(1)=2.
Funksiya qrafiki saat=(X+1)·( X–2) 2 Ox oxu ilə kəsişir saat=0, yəni nə vaxt X= –1 və X=2;
da Oy oxunu keçir X=0, yəni nə vaxt saat=4. Üç xal qazandıq: (–1; 0), (2; 0), (0; 4). Əldə olunan bütün xalları onlara bitişik olanları əlavə edərək cədvələ daxil edəcəyik.
–2
–1



–16


edir. 4 Əyri y=(x+1)(x–2) 2.
Tapşırıq №1
Biz sizə bir, iki, üç və ya daha çox düzgün cavabı olan tapşırıqları təqdim edirik. Bütün düzgün cavabların nömrələrini dairə edin.
1. Əgər  sonra funksiya
sonra funksiya
1) artır
2) azalan
3) daimi
2. Əgər
1) Artan
2) azalan
3. Əgər  , sonra funksiya
, sonra funksiya
1) Artan
2) azalan
4. Əgər  , sonra funksiya
, sonra funksiya
1) Artan 3) azalan
2) Daimi 4) Monoton
5. Funksiya  edir
edir
1) Hətta
2) Hətta yox
3) nə cüt, nə də tək
4) Dövri
5) Dövri deyil
6) Triqonometrik
7) İbtidai
6. Funksiya  edir
edir
1) hətta
2) qəribə
3) nə cüt, nə də tək
4) dövri
5) dövri deyil
6) triqonometrik
7) ibtidai
2) Weierstrass 4) Dirixlet 6) Leibniz
8) Həll  Tənliklər
Tənliklər
1) 0 3) 0 və 3 5) 2 7) 3
2) 2 və 3 4) 2 6) -5 və 1 8) 5 və 1
9) bərabərsizliyin həlli 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 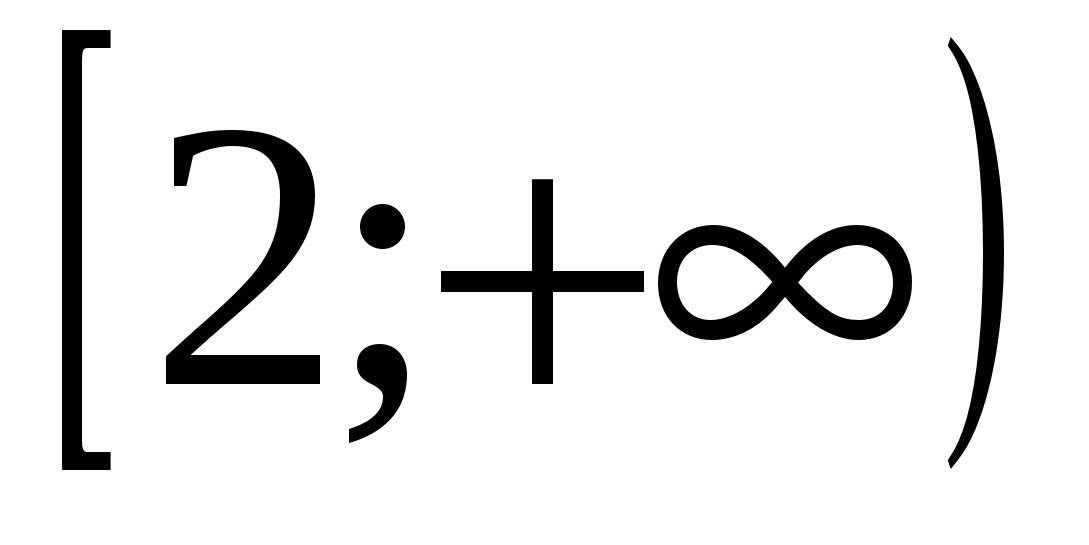
10) Metod  Məbləğ tapılır
Məbləğ tapılır
1) vektorlar
2) düz
3) seqment
11) Əgər  , sonra funksiya
, sonra funksiya
1) Konkav 3) Qabarıq 5) Azalan
2) Monoton 4) Artan 6) Sabit
12) funksiyanın təyin olunma oblastı bərabərdir 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 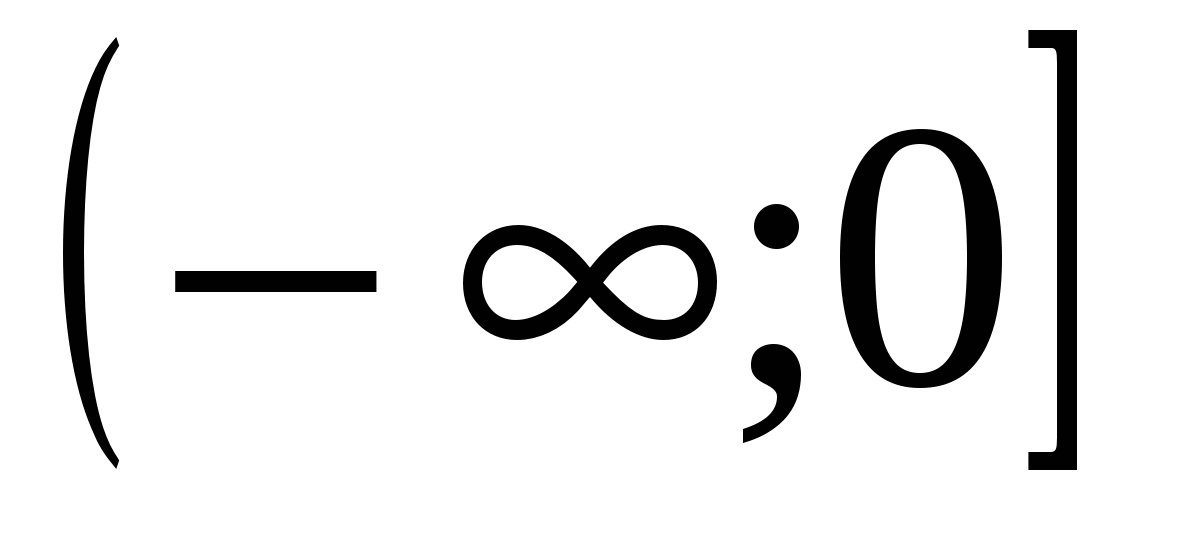
7) (-1;1)
8) 
9) 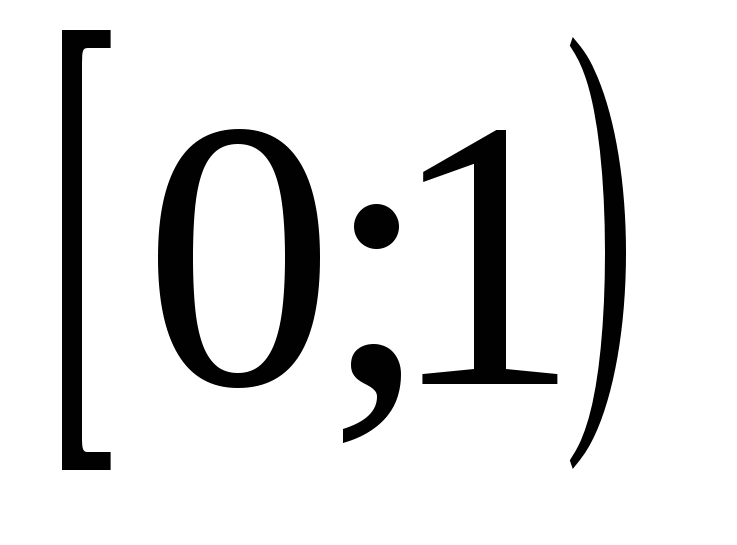
13) funksiya  edir
edir
1) göstərici
2) triqonometrik
3) güc
4) loqarifmik
14) funksiyaları y = olarsa x  onda odur
onda odur 
1) hətta
2) qəribə
3) nə cüt, nə də tək
15) funksiya  saat
saat  edir
edir

 .
.


