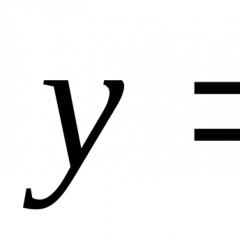Yanlış inteqralların yaxınlaşması üçün testlər. Düzgün olmayan inteqralı necə hesablamaq və onun yaxınlaşmasını tapmaq olar. Tərif və əsas xüsusiyyətlər

Teorem 12.11 (uyğun olmayan inteqralların müqayisəsi üçün test). f(x) və g(x) funksiyaları [a, ">) intervalında kəsilməz olsun və onun üzərində 0 fix) ?(x) şərtini ödəsin. Sonra inteqralın yaxınlaşmasından

inteqral yaxınlaşır

və əksinə, (12.64) inteqralının divergensiyasından (12.63) inteqralın fərqliliyi əmələ gəlir.

Sübut. Aşağıdakı qeydi təqdim edək:

Funksiya P(K) azalmır; əslində, əgər və mən 2, onda

J düzəltmək) dx>0 və sonra

Gəlin qiymətlər ardıcıllığını götürək (/?„) -> “>; sonra funksiya qiymətlərinin müvafiq ardıcıllığı (F(Rn)) monotondur və azalmır. (12.63) inteqralı yaxınlaşsın, sonra ardıcıllıq (67 () R o)) məhduddur; lakin sonra ardıcıllıq da məhduddur (F(/?„)), bu o deməkdir ki, Teorem 7.13-ə görə birləşir. Buna görə də bir məhdudiyyət var F(R) saat R-+ «>, yəni. inteqral (12.64) yaxınlaşır.

İndi teoremin ikinci hissəsini sübut edək; (12.64) inteqralı ayrılsın. Əgər (12.63) inteqralının yaxınlaşdığını fərz etsək, onda yuxarıda sübut olunduğu kimi (12.64) inteqral da yaxınlaşmalıdır ki, bu da şərtə ziddir. Teorem sübut edilmişdir. ?

Şərh. Bənzər müqayisə meyarı ikinci növ düzgün olmayan inteqrallar üçün də keçərlidir. Əgər /(x) funksiyaları və g (X) yarım intervalda davamlı [a>b) və tək nöqtənin bəzi qonşuluğundakı bütün nöqtələr üçün b tamamlandı

şərtlər 0 (x), onda Jg(x)dx inteqralının yaxınlaşmasından belə nəticə çıxır ki

J/(x)dx inteqralının, J/(x)dx inteqralının divergensiyasından -

Jg(x)dx inteqralının gücü.

Uyğun olmayan inteqralların yaxınlaşmasını öyrənmək üçün nümunələrə baxaq.

Misal 27. T. ^-.

X 3 (1 + e L)

Həll. Bu inteqraldakı inteqranı funksiya ilə müqayisə edək

Dg. Aydındır ki, -r-

X g* (1+0 x J

gral J-jdx birləşir; buna görə də, müqayisə meyarına əsasən, verilmiş 1 X

nal inteqral.

Misal 28. I-.

Həll. Bu inteqralın inteqralını 1/x funksiyası ilə müqayisə edərək,

1 intervalında (1 + x-də)/x > 1/x olduğunu görürük

şaxələndirir, ona görə də müqayisə etdikdə, bu inteqral da fərqlənir.

Sonda biz birinci növ düzgün olmayan inteqralın yaxınlaşması üçün Koşi kriteriyasını sübutsuz təqdim edirik.

12.10.4. Uyğun olmayan inteqralların mütləq və şərti yaxınlaşması

Tərif 5. Düzgün olmayan J/(x)dx inteqralı adlanır tamamilə

konvergent, J|/(x)|dx inteqralı yaxınlaşırsa.

Tərif 6. J /(x) dx düzgün olmayan inteqralı adlanır şərti olaraq oxşardır

Uzunmüddətli, əgər yaxınlaşırsa və inteqral J|/(x)|dx ayrılırsa.

Qeyd edək ki, inteqralın mütləq yaxınlaşması onun 3-cü qiymətləndirməyə görə yaxınlaşmasını nəzərdə tutur müəyyən inteqral və Koşi meyarı.

Teorem 12.13 (Diriklet-Abel testi*). /(x) funksiyası davamlı olsun və məhdud antitörəmə malik olsun F(x) [a, «>] intervalında və g(x) funksiyası bu intervalda davamlı törəməyə malikdir, x -> ©o kimi artmır və sıfıra meyl edir. Sonra düzgün olmayan inteqral

birləşir.

Sübut. J /(x)g(x)dx inteqralına hissələr üzrə inteqrasiya tətbiq edək

ixtiyari seqmentdə R R"[ ilə A, °°). Bizdə:

Teorem 12.12. Yanlış inteqralın (12.64) yaxınlaşması üçün zəruri və kifayətdir ki, istənilən e > 0 üçün belə bir ədəd tapa bilsin. A> 0, hər hansı biri üçün R" və /?", -dən böyük A, bərabərsizlik təmin edir:

Teoremin şərtlərinə görə F(x) məhdud, yəni. |F(x)| K. g(x) funksiyası x -” “> kimi artmır və sıfıra meyl edir, yəni. g(x)> 0, a g"(x)

Abel Niels Henrik (1802-1829) - norveçli riyaziyyatçı.

Teoremin şərtlərinə görə, x -> ©° üçün g(x) -» 0 olduğundan, ixtiyari e > 0 ədədi üçün ədədi tapa bilərik. A> belə ki, nə vaxt R" > L bərabərsizlik təmin ediləcək g(R") Bunu təxmin (12.68) ilə əvəz edərək, əldə edirik:

inteqralın yaxınlaşması üçün Koşi meyarına uyğundur (12.66). Teorem sübut edilmişdir. ?

Düzgün olmayan inteqralların yaxınlaşması üçün Dirixlet-Abel testindən istifadə nümunələrinə baxaq.

Misal 29. f^^dx, a>0.

Həll./(x) = sin x qoyaq, g(x)= l/x"; teoremin bütün şərtlərinin ödənildiyini, yəni bu inteqralın yaxınlaşdığını yoxlamaq asandır. a > 1 üçün bu inteqral

ral tamamilə birləşir. Həqiqətən, |günah x/xP 1/d L, inteqral J(l/x e)dx

birləşir, yəni. Müqayisə meyarına görə (Teorem 12.11) bu inteqral da mütləq yaxınlaşır.

Misal 30. Jsin x 2 dx - Fresnel inteqralı, o

Həll. Bu inteqralı cəmi kimi təqdim edək:

günah x 2 olduğundan - davamlı funksiya intervalında (0, 1J, (12.69)-da birinci inteqral mövcuddur. (12.69)-un sağ tərəfində düzgün olmayan inteqralın yaxınlaşmasını müəyyən etmək üçün /(x) = x sin x 2, g(x) = 1/x. Sonra /(x) funksiyası üçün antitörəmə F(x) = -cosx 2 /!|1, ">) intervalında məhdudlaşır və #(x) müsbətdir, x -" °° kimi sıfıra meyllidir və (1, ©о) üzərində davamlı törəmə var. Bu o deməkdir ki, Dirixlet-Abel meyarına görə (12.69)-da ikinci inteqral yaxınlaşır, yəni. Fresnel inteqralı da yaxınlaşır.

Bildiyiniz kimi, inteqralı tapmaq olduqca çətin bir iş ola bilər. Düzgün olmayan inteqralı hesablamağa başlamaq və onun ayrılan yolun sonunda tapmaq böyük məyusluq olardı. Buna görə də, bir növ funksiyaya əsaslanan ciddi hesablamalar olmadan düzgün olmayan inteqralın yaxınlaşması və ya ayrılması haqqında nəticə çıxarmağa imkan verən üsullar maraq doğurur. Aşağıda müzakirə ediləcək birinci və ikinci müqayisə teoremləri yaxınlaşma üçün düzgün olmayan inteqralların öyrənilməsinə çox kömək edir.

Qoy f(x)?0. Sonra funksiyalar

t və ya -g dəyişənlərində monoton şəkildə artır (g>0 qəbul etdiyimiz üçün -g soldan sıfıra meyl edir). Əgər arqumentlər artdıqca F 1 (t) və F 2 (-d) funksiyaları yuxarıdan məhdud qalırsa, bu, uyğun olmayan inteqralların yaxınlaşması deməkdir. Bu, qeyri-mənfi funksiyaların inteqralları üçün birinci müqayisə teoreminin əsasını təşkil edir.

x?a-da f(x) və g(x) funksiyaları aşağıdakı şərtləri ödəsin:

• 1) 0?f(x)?g(x);
• 2) f(x) və g(x) funksiyaları fasiləsizdir.

Onda inteqralın yaxınlaşmasından inteqralın yaxınlaşması, inteqralın uzaqlaşmasından isə divergensiya əmələ gəlir.

0?f(x)?g(x) və funksiyalar fasiləsiz olduğundan

Şərtə görə, inteqral yaxınlaşır, yəni. sonlu qiymətə malikdir. Beləliklə, inteqral da yaxınlaşır.

İndi inteqral ayrılsın. Fərz edək ki, inteqral yaxınlaşır, lakin sonra inteqral yaxınlaşmalıdır ki, bu da şərtə ziddir. Fərziyyəmiz yanlışdır, inteqral fərqlidir.

2-ci növ düzgün olmayan inteqrallar üçün müqayisə teoremi.

f(x) və g(x) funksiyaları üçün , x>+0 üçün limitsiz artsın. x>+0 üçün aşağıdakı bərabərsizlik yerinə yetirilir:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.

1-ci növ düzgün olmayan inteqrallar üçün müqayisə teoremi.

f(x) və g(x) funksiyası intervalında olsun və inteqrasiya seqmenti sonludur, yəni sonsuzluqla deyil, ədədlərlə məhduddur. Bəzi vəzifələr bu məhdudiyyətlərdən imtina etmək zərurətinə səbəb olur. Düzgün olmayan inteqrallar belə görünür.

Düzgün olmayan inteqralın həndəsi mənasıÇox sadə çıxır. Bir funksiyanın qrafiki olduqda y = f(x) oxun üstündədir öküz, müəyyən inteqral əyri ilə məhdudlaşan əyrixətti trapezoidin sahəsini ifadə edir y = f(x) , x oxu və ordinatlar x = a , x = b. Öz növbəsində, düzgün olmayan inteqral xətlər arasında bağlanmış qeyri-məhdud (sonsuz) əyri xətti trapezoidin sahəsini ifadə edir. y = f(x) (aşağıdakı şəkildə - qırmızı), x = a və absis oxu.

Yanlış inteqrallar digər sonsuz intervallar üçün də eyni şəkildə müəyyən edilir:

Sonsuz əyri trapezoidin sahəsi sonlu ədəd ola bilər, bu halda düzgün olmayan inteqrala konvergent deyilir. Sahə də sonsuz ola bilər və bu halda düzgün olmayan inteqral divergent adlanır.

Düzgün olmayan inteqralın özünün əvəzinə inteqralın limitindən istifadə. Düzgün olmayan inteqralı qiymətləndirmək üçün müəyyən inteqralın limitindən istifadə etmək lazımdır. Əgər bu hədd mövcuddursa və sonludursa (sonsuzluğa bərabər deyil), onda düzgün olmayan inteqral konvergent, əks halda isə divergent adlanır. Dəyişənin limit işarəsi altında nəyə meyl etməsi birinci və ya ikinci növ düzgün olmayan inteqralla məşğul olmağımızdan asılıdır. Gəlin bu barədə indi öyrənək.

Birinci növ düzgün olmayan inteqrallar - sonsuz hədləri və onların yaxınlaşması

Sonsuz yuxarı həddi olan yanlış inteqrallar

Deməli, düzgün olmayan inteqralın yazılması adi müəyyən inteqraldan inteqrasiyanın yuxarı həddinin sonsuz olması ilə fərqlənir.

Tərif. Davamlı funksiyanın sonsuz yuxarı həddi olan düzgün olmayan inteqral f(x) -dən aralığında a əvvəl ∞ bu funksiyanın inteqralının yuxarı həddi ilə inteqral həddi adlanır b və inteqrasiyanın aşağı həddi a bir şərtlə ki, inteqrasiyanın yuxarı həddi məhdudiyyətsiz artsın, yəni.

.

Əgər bu hədd mövcuddursa və sonsuzluğa deyil, hansısa ədədə bərabərdirsə düzgün olmayan inteqrala konvergent deyilir, və limitin bərabər olduğu ədəd onun qiyməti kimi qəbul edilir. Əks halda düzgün olmayan inteqrala divergent deyilir və ona heç bir məna verilmir.

Nümunə 1. Düzgün olmayan inteqralı hesablayın(birləşərsə).

Həll. Yanlış inteqralın tərifinə əsasən tapırıq

Limit mövcud olduğundan və 1-ə bərabər olduğundan, bu düzgün olmayan inteqral yaxınlaşır və 1-ə bərabərdir.

Aşağıdakı misalda inteqral 1-ci misaldakı ilə demək olar ki, eynidir, yalnız x dərəcəsi iki deyil, alfa hərfidir və tapşırıq konvergensiya üçün düzgün olmayan inteqralı öyrənməkdir. Yəni, suala cavab vermək qalır: bu düzgün olmayan inteqral alfanın hansı dəyərlərində yaxınlaşır və hansı dəyərlərdə fərqlənir?

Misal 2. Konvergensiya üçün uyğun olmayan inteqralı yoxlayın(inteqrasiyanın aşağı həddi sıfırdan böyükdür).

Həll. Əvvəlcə bunu fərz edək, sonra

Nəticə ifadəsində biz limitə keçirik:

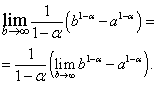
Asanlıqla görmək olar ki, sağ tərəfdəki limit mövcud olduqda və sıfıra bərabərdir, yəni olduqda, mövcud deyil.

Birinci halda, yəni nə vaxt . Əgər, onda və mövcud deyil.

Araşdırmamızın nəticəsi belədir: bu düzgün olmayan inteqral yaxınlaşır və ayrılır at.

Nyuton-Leybniz düsturunun öyrənilən düzgün olmayan inteqral növünə tətbiqi , siz ona çox bənzəyən aşağıdakı düsturu əldə edə bilərsiniz:

.

Bu ümumiləşdirilmiş Nyuton-Leybniz düsturudur.

Misal 3. Düzgün olmayan inteqralı hesablayın(birləşərsə).

Bu inteqralın həddi mövcuddur:

İlkin inteqralı ifadə edən cəmini təşkil edən ikinci inteqral:

Bu inteqralın həddi də mövcuddur:

.

Biz iki inteqralın cəmini tapırıq ki, bu da iki sonsuz həddi olan ilkin qeyri-müəyyən inteqralın qiymətidir:

İkinci növ düzgün olmayan inteqrallar - qeyri-məhdud funksiyalardan və onların yaxınlaşmasından

Qoy funksiya olsun f(x) -dən seqment üzrə verilmişdir a əvvəl b və bununla bağlı məhdudiyyətsizdir. Tutaq ki, funksiya nöqtədə sonsuzluğa gedir b , seqmentin bütün digər nöqtələrində isə davamlıdır.

Tərif. Funksiyanın düzgün olmayan inteqralı f(x) olan seqmentdə a əvvəl b bu funksiyanın inteqralının yuxarı həddi ilə inteqral həddi adlanır c , əgər cəhd edərkən c Kimə b funksiya limitsiz və nöqtədə artır x = b funksiyası müəyyən edilməmişdir, yəni.

.

Əgər bu hədd mövcuddursa, onda ikinci növ düzgün olmayan inteqralı konvergent, əks halda divergent adlanır.

Newton-Leibniz düsturundan istifadə edərək, əldə edirik.

1. Sonsuz həddi olan qeyri-müvafiq inteqrallar

İnteqralın inteqral cəmlərin həddi kimi tərifini xatırlayaq:

Tərif inteqral intervalının sonlu olduğunu və f(x) funksiyasının onun daxilində davamlı olduğunu qəbul edir. Bu fərziyyələrin pozulması düzgün olmayan inteqrallara gətirib çıxarır.

Tərif.İnteqral qeyri-müəyyən artdıqca sonlu həddə meyl edərsə "b", onda bu hədd f (x) funksiyasının sonsuz yuxarı həddi olan düzgün olmayan inteqral adlanır və simvolu ilə işarələnir.

Bu halda düzgün olmayan inteqralın mövcud olduğu və ya yaxınlaşdığı deyilir.

Göstərilən hədd mövcud deyilsə və ya mövcuddur, lakin sonsuzdursa, inteqralın mövcud olmadığı və ya ayrıldığı deyilir.

Sonsuz aşağı həddi olan düzgün olmayan inteqral oxşar şəkildə müəyyən edilir:

İki sonsuz sərhədi olan düzgün olmayan inteqral aşağıdakı kimi verilir:

burada c Ox oxundakı hər hansı sabit nöqtədir.

Beləliklə, düzgün olmayan inteqralların sonsuz aşağı həddi, sonsuz yuxarı həddi və həmçinin iki sonsuz həddi ola bilər.

Konvergensiya əlamətləri. Mütləq və şərti yaxınlaşma

İnteqral yalnız inteqralların hər biri mövcud olduqda mövcuddur: və .

Misal.İnteqralın yaxınlaşmasını yoxlayın

c = 0 fərz etsək, alırıq:

olanlar. inteqral yaxınlaşır.

Bəzən düzgün olmayan inteqralı hesablamağa ehtiyac olmur, ancaq onu başqa bir inteqralla müqayisə edərək yaxınlaşıb-uzlaşmadığını bilmək kifayətdir.

Yanlış inteqrallar üçün müqayisə teoremi.

İntervaldakı f (x) funksiyasının birinci növdən bir neçə (sonlu sayda) kəsilmə nöqtəsi olsun, bu “maneə” seqmenti kəsilmə nöqtələri olan bir neçə seqmentə bölmək, hər bir fərdi bölmə üzrə müəyyən inteqralları hesablamaqla və asanlıqla aradan qaldırıla bilər. nəticələrin əlavə edilməsi.

Seqmentin uclarından birinə yaxınlaşdıqda qeyri-məhdud olan funksiyanın müəyyən inteqralını nəzərdən keçirək, məsələn, .

(Belə hallarda adətən belə deyirlər: ''Funksiya inteqrasiya intervalının sağ ucunda sonsuz fasiləsizliyə malikdir.'').

Aydındır ki, inteqralın adi tərifi burada öz mənasını itirir.

Tərif. £ x üçün davamlı f(x) funksiyasının düzgün olmayan inteqralı< b и неограниченной при x ® b - 0, называется предел:

Seqmentin sol ucunda sonsuz fasiləsi olan funksiyanın düzgün olmayan inteqralı oxşar şəkildə müəyyən edilir:

Beləliklə, [-1, 0] bölməsində inteqral ayrılır.

Bu o deməkdir ki, inteqral bölmədə də ayrılır.

Beləliklə, bu inteqral bütün intervalda fərqlənir [-1, 1]. Qeyd edək ki, əgər x = 0 nöqtəsində inteqranın kəsildiyinə diqqət yetirmədən bu inteqralı hesablamağa başlasaq, düzgün olmayan nəticə əldə etmiş olarıq. Həqiqətən,

, bu mümkün deyil.

Deməli, fasiləsiz funksiyanın düzgün inteqralını öyrənmək üçün onu bir neçə inteqrala “parçalamaq” və onları öyrənmək lazımdır.

Əgər inteqralın (sonlu) inteqrasiya intervalında ikinci növ kəsikliyi varsa, biz ikinci növ düzgün olmayan inteqraldan danışırıq.

10.2.1 Tərif və əsas xüsusiyyətlər

İnteqrasiya intervalını $\left[ a, \, b \right ]$ ilə işarə edək; bu ədədlərin hər ikisi aşağıda sonlu hesab edilir. Yalnız 1 kəsilmə varsa, o, ya $a$ nöqtəsində, ya da $b$ nöqtəsində və ya $(a,\,b)$ intervalının daxilində yerləşə bilər. Əvvəlcə $a$ nöqtəsində ikinci növ kəsilmənin olduğu, digər nöqtələrdə isə inteqral funksiyasının davamlı olduğu halı nəzərdən keçirək. Beləliklə, biz inteqraldan danışırıq

\begin(tənlik) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(tənlik)

və $x \rightarrow a+0$ olduqda $f(x) \rightarrow \infty $. Əvvəlki kimi ilk iş bu ifadəyə məna verməkdir. Bunu etmək üçün inteqralı nəzərdən keçirin

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

Tərif. Sonlu bir hədd olsun

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

Sonra ikinci növ (22) uyğunsuz inteqral yaxınlaşır və ona $A$ dəyəri təyin edilir; $f(x)$ funksiyasının özü $\left[ a, \ intervalında inteqral oluna bilir. , b\sağ]$.

İnteqrasiya intervalının yuxarı həddində inteqran funksiyasında ikinci növ kəsilmə olduqda variantı nəzərdən keçirək. Bu hal $x=-t$ dəyişəninin dəyişilməsini etməklə və sonra inteqrasiyanın sərhədlərini yenidən təşkil etməklə əvvəlki vəziyyətə endirilə bilər.

İnteqral funksiyasının $c \in (a,\,b)$ nöqtəsində inteqrasiya intervalı daxilində ikinci növ fasiləsizliyə malik olduğu variantı nəzərdən keçirək. Bu halda, orijinal inteqral

\begin(tənlik) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(tənlik)

cəmi kimi təqdim olunur

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Tərif. Əgər $I_1, \, I_2$ inteqrallarının hər ikisi yaxınlaşırsa, onda düzgün olmayan inteqral (23) yaxınlaşma adlanır və $I_1, \, I_2$ inteqrallarının cəminə, $f(x)$ funksiyasına bərabər qiymət verilir. $\left [a, \, b\right]$ intervalında inteqrasiya olunan adlanır. Əgər $I_1,\, I_2$ inteqrallarından ən azı biri divergentdirsə, düzgün olmayan inteqral (23) divergent adlanır.

2-ci növ konvergent uyğunsuz inteqrallar adi müəyyən inteqralların bütün standart xassələrinə malikdirlər.

1. Əgər $f(x)$, $g(x)$ $\left[ a, \,b \right ]$ intervalında inteqral oluna bilirsə, onda onların $f(x)+g(x)$ cəmi həmçinin bu intervalda inteqrasiya edilə bilər və \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Əgər $f(x)$ $\left[ a, \, b \right ]$ intervalında inteqrasiya oluna bilirsə, onda hər hansı $C$ sabiti üçün $C\cdot f(x)$ funksiyası da bu intervalda inteqrasiya edilə bilən və \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Əgər $f(x)$ $\left[ a, \, b \right ]$ intervalında və bu $f(x)>0$ intervalında inteqrasiya oluna bilirsə, onda \[ \int _a^ (b ) f(x)dx\,>\,0. \] 4. Əgər $f(x)$ $\left[ a, \, b \right ]$ intervalında inteqrallana bilirsə, onda hər hansı $c\in (a, \,b)$ üçün inteqrallar \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] də birləşir və \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (inteqralın interval üzrə əlavəliyi).

İnteqralı nəzərdən keçirək

\begin(tənlik) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(tənlik)

Əgər $k>0$ olarsa, inteqral $x \rightarrow +0$ kimi $\infty$-a meyl edir, ona görə də inteqral ikinci növdən uyğun deyil. Funksiyanı təqdim edək

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

Bu halda antiderivativ məlumdur, belə ki

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

$k \neq 1$ üçün,

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

$k = 1$ üçün. $\epsilon \rightarrow +0$-da davranışı nəzərə alaraq belə nəticəyə gəlirik ki, inteqral (20) $k-da birləşir.

10.2.2 2-ci növ düzgün olmayan inteqralların yaxınlaşması üçün sınaqlar

Teorem (müqayisə üçün ilk əlamət). $x\in (a,\,b)$ və $0 üçün $f(x)$, $g(x)$ davamlı olsun 1. Əgər inteqral \[ \int _a^(b)g(x) dx \] birləşir, sonra \[ \int _a^(b)f(x)dx inteqralı birləşir. \] 2. \[ \int _a^(b)f(x)dx \] inteqralı ayrılırsa, onda \[ \int _a^(b)g(x)dx inteqralı ayrılır. \]

Teorem (ikinci müqayisə meyarı). Qoy $f(x)$, $g(x)$ $x\in (a,\,b)$ üçün davamlı və müsbət olsun və sonlu həddi olsun.

\[ \theta = \lim_(x \rightarrow a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Sonra inteqrallar

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

eyni vaxtda birləşir və ya ayrılır.