Tənlik nədir?

Cəbrdə ilk addımlarını atanlar, təbii ki, materialın ən nizamlı təqdimatını tələb edirlər. Buna görə də, tənliyin nə olduğu haqqında məqaləmizdə biz təkcə tərif verməyəcəyik, həm də verəcəyik müxtəlif təsnifatlar misallarla tənliklər.

Tənlik nədir: ümumi anlayışlar

Beləliklə, tənlik latın hərfi ilə işarələnən naməlum ilə bərabərlik növüdür. Harada ədədi dəyər düzgün bərabərliyi əldə etməyə imkan verən bir hərf tənliyin kökü adlanır. Bu barədə məqaləmizdə daha çox oxuya bilərsiniz, lakin biz tənliklərin özləri haqqında danışmağa davam edəcəyik. Tənliyin (və ya dəyişənlərin) arqumentləri naməlumdur və tənliyin həlli onun bütün köklərini və ya köklərinin olmamasını tapmaqdır.

Tənliklərin növləri

Tənliklər iki böyük qrupa bölünür: cəbri və transsendental.

• Cəbr, tənliyin kökünü tapmaq üçün yalnız cəbri əməliyyatlardan istifadə edildiyi bir tənlikdir - 4 arifmetik, həmçinin təbii kökün eksponentasiyası və çıxarılması.
• Transsendental tənlik, kökü tapmaq üçün qeyri-cəbr funksiyalarının istifadə edildiyi tənlikdir: məsələn, triqonometrik, loqarifmik və s.

Cəbri tənliklər arasında da var:

• tam ədədlər - naməlumlara münasibətdə tam cəbri ifadələrdən ibarət hər iki hissə ilə;
• kəsr - say və məxrəcdə tam cəbri ifadələri ehtiva edən;
• irrasional - burada cəbri ifadələr kök işarəsi altındadır.

Onu da nəzərə alın ki, kəsrli və irrasional tənliklər bütün tənliklərin həllinə endirilə bilər.

Transsendental tənliklər aşağıdakılara bölünür:

• Eksponensial tənliklər dəyişəni eksponent kimi ehtiva edən tənliklərdir. Onlar vahid bazaya və ya eksponentə keçmək, ümumi amili mötərizədən çıxarmaq, faktorinq və bəzi digər üsullarla həll olunur;
• loqarifmik - loqarifmli tənliklər, yəni naməlumların loqarifmlərin öz daxilində olduğu tənliklər. Bu cür tənlikləri həll etmək çox çətindir (məsələn, əksər cəbri tənliklərdən fərqli olaraq), çünki bu, möhkəm riyazi təlim tələb edir. Burada ən vacibi loqarifmli tənlikdən onlarsız tənliyə keçmək, yəni tənliyi sadələşdirməkdir (loqarifmləri silməyin bu üsulu potensiasiya adlanır). Əlbəttə ki, gücləndirin loqarifmik tənlik yalnız eyni ədədi əsaslara malik olduqda və əmsalları olmadıqda mümkündür;
• triqonometrik işarələr altında dəyişənləri olan tənliklərdir triqonometrik funksiyalar. Onların həlli triqonometrik funksiyaların ilkin mənimsənilməsini tələb edir;
• qarışıq müxtəlif növlərə aid hissələri olan diferensiallaşdırılmış tənliklərdir (məsələn, parabolik və elliptik hissələrlə və ya elliptik və hiperbolik və s.).

Naməlumların sayına görə təsnifata gəlincə, hər şey sadədir: bir, iki, üç və s. naməlum olan tənliklər fərqləndirilir. Polinomun sol tərəfində olan dərəcəyə əsaslanan başqa bir təsnifat da var. Buna əsasən xətti, kvadrat və kub tənlikləri fərqləndirilir. Xətti tənliklər müvafiq olaraq 1-ci dərəcəli, kvadratik - 2-ci və kub tənlikləri də adlandırmaq olar. Yaxşı, indi bu və ya digər qrupun tənliklərinə nümunələr verək.

Müxtəlif növ tənliklərin nümunələri

Cəbri tənliklərə nümunələr:

• ax + b = 0
• ax 3 + bx 2 + cx+ d= 0
• ax 4 + bx 3 + cx 2 + bx + a= 0
  (a 0-a bərabər deyil)

Transsendental tənliklərə nümunələr:

• cos x = x log x = x−5 2 x = logx+x 5 +40

Tam tənliklərə nümunələr:

• (2+x)2 = (2+x)(55x-4) (x2-12x+10)4 = (3x+10)4 (4x2+3x-10)2=9x4

Kəsr tənliklərinə misal:

• 15 x + — = 5x - 17 x

İrrasional tənliklərə misal:

• √2kf(x)=g(x)

Xətti tənliklərə nümunələr:

• 2x+7=0 x - 3 = 2 - 4x 2x+3=5x+5 - 3x - 2

Kvadrat tənliklərə nümunələr:

• x 2 +5x−7= 0 3x 2 +5x−7= 0 11x 2 −7x+3 = 0

Kub tənliklərinə nümunələr:

• x 3 -9x 2 -46x+120=0 x 3 - 4x 2 + x + 6 = 0

Eksponensial tənliklərə nümunələr:

• 5 x+2 = 125 3 x 2 x = 8 x+3 3 2x +4 3 x -5 = 0

Loqarifmik tənliklərə nümunələr:

• log 2 x= 3 log 3 x= -1

Triqonometrik tənliklərə nümunələr:

• 3sin 2 x + 4sin x cosx + cos 2 x = 2 sin(5x+π/4) = ctg(2x-π/3) sinx + cos 2 x + tan 3 x = ctg 4 x

Qarışıq tənliklərə nümunələr:

• log x (log 9 (4⋅3 x −3))=1 |5x−8|+|2⋅5x+3|=13

Əlavə etmək qalır ki, müxtəlif növ tənlikləri həll etmək üçün müxtəlif üsullardan istifadə olunur. Yaxşı, demək olar ki, hər hansı bir tənliyi həll etmək üçün sizə təkcə cəbr deyil, həm də triqonometriya və çox vaxt çox dərin bilik lazımdır.

Riyaziyyat. Cəbr. Həndəsə. Triqonometriya

CƏBR: Tənliklər və tənliklər sistemləri

4.2. Tənliklərin növləri və onların həlli üsulları

Hər iki verilmiş tənliyi təmin edən dəyişənin dəyərlərini tapmaq lazım olduqda, onun verildiyini deyirik, tənliklər sistemi. Buruq mötərizə sistemi göstərmək üçün istifadə olunur:

Bir dəyişən formalı bir neçə tənlik tənliklər toplusu, əgər vəzifə hər biri bu tənliklərdən ən azı birinin kökü olan dəyişənin bütün bu cür dəyərlərini tapmaqdırsa. Kvadrat mötərizə əhalini göstərmək üçün istifadə olunur:

Modul işarəsi altında dəyişən olan tənliklər.

Ədədin mütləq dəyəri A aşağıdakı kimi müəyyən edilir:

Misal: Tənliyi həll edin

.

Həll yolu: Əgər

, Bu . Bunu belə yaza bilərsiniz:

Eq.

Biz tapdıq X= -9. Bununla belə, dəyişənin bu dəyəri ilə bərabərsizlik təmin edilmir, yəni tapılan dəyər bu tənliyin kökü deyil., Bu və bu tənlik formasını alacaq. Bunu belə yaza bilərsiniz:

Eq.

Biz tapdıq . Bərabərsizlik doğrudur, yəni - bu tənliyin kökü..

Məxrəcində dəyişən olan tənliklər.

Formanın tənliklərini nəzərdən keçirin

. (1)

(1) tipli tənliyin həlli aşağıdakı müddəaya əsaslanır: kəsr 0-a bərabərdir, o halda ki, onun payı 0-a, məxrəci isə sıfıra bərabərdir.

Yuxarıda göstərilənlərə uyğun olaraq, tənliyin həlli

iki mərhələdə həyata keçirilir: əvvəlcə tənliyi həll etmək lazımdır, və sonra dəyişənin tapılmış dəyərləri ilə olub olmadığını öyrənin. X məxrəc 0-da. Əgər q(x) ¹ 0 , sonra tənliyin tapılmış köküeyni zamanda (1) tənliyinin köküdür; Əgərq(x) = 0, sonra tənliyin nəticə kökühəm də (1) tənliyinin köküdür. Nəticə sistem:

Tənliyin domeni

f(x) = g(x) dəyişənin bütün bu dəyərlərinin çoxluğuna zəng edin X, bunun üçün ifadəf(x), və ifadəsi g(x)məna kəsb etmək.

Əgər tənliyin çevrilməsi prosesində onun tərif dairəsi genişlənibsə, onda kənar köklər yarana bilər. Buna görə dəyişənin bütün tapılmış dəyərləri orijinal tənliyə əvəz etməklə və ya orijinal tənliyin tərif sahəsindən istifadə etməklə yoxlanılmalıdır.

Rasional tənliklər.

tənlik

f(x) = g(x) çağırdı rasional, Əgər f(x) və g(x)-rasional ifadələr. Üstəlik, əgər f(x) və g(x)- tam ifadələr, sonra tənlik çağırılır bütöv ;ifadələrdən ən azı biri olarsaf(x), g(x)kəsrdir, onda rasional tənlikf(x) = g(x) çağırdı fraksiyalı .

Rasional tənliyi həll etmək üçün sizə lazımdır:

1. bütün mövcud kəsrlərin ortaq məxrəcini tapın;
2. hər iki hissəsini ümumi məxrəcə vuraraq bu tənliyi tamla əvəz edin;
3. Nəticədə bütöv tənliyi həll edin;
4. Ortaq məxrəci yox edənləri onun kökündən sil.

Tənliyin həlli

p(x) = 0 faktorizasiya üsulu. p(x) faktorlara bölünə bilər: , sonra tənlik formasını alır . Əgər A- tənliyin kökü, Bu , buna görə də nömrələrdən ən azı biri0-a bərabərdir.

Bunun əksi də doğrudur: əgər X

= A- tənliklərdən ən azı birinin kökü, , , Bu A- tənliyin kökü. Yəni

Tənliklərin həlli

yeni dəyişən təqdim etməklə.

Metodun mahiyyətini bir nümunə ilə izah edək.

Misal: Tənliyi həll edin

.

Həll edək

, tənliyini alırıq, harada tapırıq . Problem bir sıra tənliklərin həllinə gəlir

Û

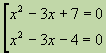
Birinci kvadrat tənliyin həqiqi kökləri yoxdur, ona görə də onun diskriminantı mənfidir. İkincidən tapırıq

. Bunlar verilmiş tənliyin kökləridir.

Formanın tənliyinə biquadratic deyilir

, Harada A ¹ 0. Biquadratic tənlik yeni dəyişən daxil etməklə həll edilir: qoyulması , kvadrat tənliyə çatırıq .

İrrasional tənliklər.

Məntiqsiz

dəyişənin kök işarəsi altında və ya kəsr gücünə yüksəltmə işarəsi altında yer aldığı tənlikdir. Belə tənliklərin həlli üsullarından biri tənliyin hər iki tərəfini eyni gücə qaldırmaq üsuludur:

A) verilmiş irrasional tənliyi formaya çevirin:

;

B) yaranan tənliyin hər iki tərəfini yuxarı qaldırırıq

n-ci dərəcə:

;

B) nəzərə alaraq

, tənliyini alırıq

f(x) = g(x);

)Tənliyi həll edirik və yoxlama aparırıq, çünki tənliyin hər iki tərəfini bərabər gücə qaldırmaq kənar köklərin yaranmasına səbəb ola bilər. Bu yoxlama dəyişənin tapılmış dəyərlərini orijinal tənliyə əvəz etməklə həyata keçirilir.

Müəllif hüququ © 2005-2013 Xenoid v2.0

Sayt materiallarından istifadə aktiv keçid şərti ilə mümkündür.

Məxfiliyinizi qorumaq bizim üçün vacibdir. Bu səbəbdən biz sizin məlumatlarınızı necə istifadə etdiyimizi və saxladığımızı təsvir edən Məxfilik Siyasəti hazırlamışıq. Zəhmət olmasa məxfilik təcrübələrimizi nəzərdən keçirin və hər hansı sualınız varsa, bizə bildirin.

Şəxsi məlumatların toplanması və istifadəsi

Şəxsi məlumat müəyyən bir şəxsi müəyyən etmək və ya əlaqə saxlamaq üçün istifadə edilə bilən məlumatlara aiddir.

İstənilən vaxt bizimlə əlaqə saxladığınız zaman sizdən şəxsi məlumatlarınızı təqdim etməyiniz tələb oluna bilər.

Aşağıda toplaya biləcəyimiz şəxsi məlumat növlərinə və bu cür məlumatlardan necə istifadə edə biləcəyimizə dair bəzi nümunələr verilmişdir.

Hansı şəxsi məlumatları toplayırıq:

• Saytda sorğu göndərdiyiniz zaman biz toplaya bilərik müxtəlif məlumatlar adınız, telefon nömrəniz, ünvanınız daxil olmaqla E-poçt və s.

Şəxsi məlumatlarınızı necə istifadə edirik:

• Topladığımız şəxsi məlumatlar bizə unikal təkliflər, promosyonlar və digər tədbirlər və qarşıdan gələn tədbirlərlə bağlı sizinlə əlaqə saxlamağa imkan verir.
• Zaman-zaman biz sizin şəxsi məlumatlarınızdan vacib bildirişlər və kommunikasiyalar göndərmək üçün istifadə edə bilərik.
• Təqdim etdiyimiz xidmətləri təkmilləşdirmək və sizə xidmətlərimizlə bağlı tövsiyələr vermək üçün auditlərin aparılması, məlumatların təhlili və müxtəlif tədqiqatların aparılması kimi şəxsi məlumatlardan daxili məqsədlər üçün də istifadə edə bilərik.
• Əgər siz uduş tirajında, müsabiqədə və ya oxşar təşviqatda iştirak edirsinizsə, biz bu cür proqramları idarə etmək üçün təqdim etdiyiniz məlumatdan istifadə edə bilərik.

Üçüncü tərəflərə məlumatların açıqlanması

Sizdən alınan məlumatları üçüncü şəxslərə açıqlamırıq.

İstisnalar:

• Zəruri hallarda - qanuna uyğun olaraq, məhkəmə qaydasında, məhkəmə icraatında və/və ya ictimai sorğu və ya sorğular əsasında dövlət qurumları Rusiya Federasiyasının ərazisində - şəxsi məlumatlarınızı açıqlayın. Bu cür açıqlamanın təhlükəsizlik, hüquq-mühafizə və ya digər ictimai əhəmiyyətli məqsədlər üçün zəruri və ya uyğun olduğunu müəyyən etsək, sizinlə bağlı məlumatları da açıqlaya bilərik.
• Yenidən təşkil etmə, birləşmə və ya satış halında, biz topladığımız şəxsi məlumatları müvafiq varis üçüncü tərəfə ötürə bilərik.

Şəxsi məlumatların qorunması

Biz şəxsi məlumatlarınızı itkidən, oğurluqdan və sui-istifadədən, habelə icazəsiz daxil olmaqdan, açıqlamadan, dəyişdirilməkdən və məhv olmaqdan qorumaq üçün inzibati, texniki və fiziki tədbirləri görürük.

Şirkət səviyyəsində məxfiliyinizə hörmət etmək

Şəxsi məlumatlarınızın təhlükəsiz olmasını təmin etmək üçün biz əməkdaşlarımıza məxfilik və təhlükəsizlik standartlarını çatdırırıq və məxfilik təcrübələrini ciddi şəkildə tətbiq edirik.

Cəbri tənliklərin növləri və onların həlli üsulları

Riyaziyyat, cəbri tənliklərin həlli ilə maraqlanan tələbələr üçün daha yüksək dərəcələr təsirli üsul kökləri tez tapmaq, qalanı x –  binomuna və ya ax + b ilə bölmək Horner sxemidir.

Hornerin sxemini nəzərdən keçirək.

P(x)-i x – -ə bölərkən natamam hissəni işarə edək.

Q (x) = b 0 x n -1 + b 1 x n -2 + ... + b n -1, qalan isə b n-dir.

P(x) = Q (x)(x–) + b n olduğundan, bərabərlik yerinə yetirilir.

a 0 x n + а 1 x n -1 + … + а n = (b 0 x n -1 + b 1 x n -2 + … + b n -1)(х– ) + b n

Sağ tərəfdəki mötərizələri açaq və əmsalları müqayisə edək bərabər dərəcələr x sol və sağ. Alırıq ki, a 0 = b 0 və 1  k  n üçün a k = b k -  b k -1 münasibətləri saxlanılır. Buradan belə çıxır ki, b 0 = a 0 və b k = a k +  b k -1, 1  k  n.

Q (x) polinomunun əmsallarının və b n qalığının hesablanmasını cədvəl şəklində yazırıq:

a 0

a 1

a 2

A n-1

A n

b 0 = a 0

b 1 = a 1 +  b 0

b 2 = a 2 +  b 1

b n-1 = a n-1 +  b n-2

b n = a n +  b n-1

Misal 1. 2x 4 – 7x 3 – 3x 2 + 5x – 1 polinomunu x + 1-ə bölün.

Həll. Hornerin sxemindən istifadə edirik.

2x 4 – 7x 3 – 3x 2 + 5x – 1-i x + 1-ə böldükdə 2x 3 – 9x 2 + 6x – 1 alırıq.

Cavab: 2 x 3 – 9x 2 + 6x – 1

Misal 2. P(3) hesablayın, burada P(x) = 4x 5 – 7x 4 + 5x 3 – 2x + 1

Həll. Bezout teoremindən və Horner sxemindən istifadə edərək əldə edirik:

Cavab: P(3) = 535

Məşq edin

Horner diaqramından istifadə edərək polinomu bölün

4x + 2-də x 3 – x 5 + 132 – 8x 2;

2) Çoxhədlini bölün

2x 2 – 3x 3 – x + x 5 + 1 x + 1 üzərində;

3) x = 7 üçün P 5 (x) = 2x 5 – 4x 4 – x 2 + 1 polinomunun qiymətini tapın.

1.1. Tam əmsallı tənliklərin rasional köklərinin tapılması

Rasional kökləri tapmaq üsulu cəbri tənlik tam əmsallı aşağıdakı teoremlə verilir.

Teorem: Tam ədədli əmsallı tənliyin rasional kökləri varsa, onlar sərbəst terminin bölənini aparıcı əmsalın böləninə bölən əmsaldır.

Sübut: a 0 x n + a 1 x n -1 + … + a n = 0

Qoy x = p/ q rasional kökdür, q, p müştərəkdir.

p/q kəsrini tənliyə əvəz edib məxrəcdən azad edərək əldə edirik.

a 0 r n + a 1 p n -1 q + … + a n -1 pq n -1 + a n q n = 0 (1)

(1)-i iki şəkildə yenidən yazaq:

a n q n = р(– а 0 р n -1 – а 1 р n -2 q – … – а n -1 q n -1) (2)

a 0 r n = q (– а 1 р n -1 –… – а n -1 рq n -2 – а n q n -1) (3)

(2) bərabərliyindən belə nəticə çıxır ki, a n q n p-ə bölünür və ondan q n və p kobuddur, onda a n p-ə bölünür. Eynilə, (3) bərabərliyindən belə nəticə çıxır ki, 0 q-a bölünür. Teorem sübut edilmişdir.

Misal 1. 2x 3 – 7x 2 + 5x – 1 = 0 tənliyini həll edin.

Həll. Tənliyin tam kökləri yoxdur; biz tənliyin rasional köklərini tapırıq. Tənliyin kökü p / q azalmayan kəsir olsun, onda p sərbəst müddətin bölənləri arasında tapılır, yəni. Rəqəmlər arasında  1 və q aparıcı əmsalın müsbət bölənləri arasında: 1; 2.

Bunlar. tənliyin rasional kökləri  1,  1/2 ədədləri arasında axtarılmalıdır, P 3 (x) = 2x 3 – 7x 2 + 5x – 1, P 3 (1)  0, P 3 (–1) işarəsi verilir.  0,

P 3 (1/2) = 2/8 – 7/4 + 5/2 – 1 = 0, 1/2 tənliyin köküdür.

2x 3 – 7x 2 + 5x – 1 = 2x 3 – x 2 – 6 x 2 + 3x + 2x – 1 = 0.

Biz əldə edirik: x 2 (2x – 1) – 3x (2x – 1)+ (2x – 1) = 0; (2x – 1)(x 2 – 3x + 1) = 0.

İkinci amili sıfıra bərabərləşdirmək və tənliyi həll etməklə, əldə edirik

Cavab:
,

Məşqlər

Tənlikləri həll edin:

6x 3 – 25x 2 + 3x + 4 = 0;

6x 4 – 7x 3 – 6x 2 + 2x + 1 = 0;

3x 4 – 8x 3 – 2x 2 + 7x – 1 = 0;

1.2. Qarşılıqlı tənliklər və həll üsulları

Tərif. Naməlumla bağlı tam gücləri olan tənlik, sol tərəfin uclarından bərabər məsafədə olan əmsalları bir-birinə bərabər olduqda, təkrarlanan adlanır, yəni. formanın tənliyi

A x n + bx n -1 + cx n -2 + … + cx 2 + bx + a = 0

Qarşılıqlı tənlik tək dərəcə

A x 2 n +1 + bx 2 n + cx 2 n -1 + … + cx 2 + bx + a = 0

həmişə x = – 1 kökə malikdir. Buna görə də o, x + 1 = 0 və  x 2 n +  x 2 n -1 + … +  x +  = 0 tənliyinin birləşməsinə bərabərdir. Son tənlik a. cüt dərəcəli qarşılıqlı tənlik. Beləliklə, istənilən dərəcədəki qarşılıqlı tənliklərin həlli cüt dərəcəli qarşılıqlı tənliyin həllinə endirilir.

Bunu necə həll etmək olar? Cüt dərəcəli qarşılıqlı tənlik verilsin

A x 2 n + bx 2 n -1 + … + dx n +1 + ex n + dx n -1 + … + bx + a = 0

Qeyd edək ki, x = 0 tənliyin kökü deyil. Sonra tənliyi x n-ə bölürük, alırıq

A x n + bx n -1 + … + dx + e + dx -1 + … + bx 1- n + аx -n = 0

Sol tərəfin şərtlərini cüt-cüt qruplaşdırırıq

A( x n + x - n ) + b (x n -1 + x -(n -1) + … + d(x + x -1 ) + e = 0

X + x -1 = y əvəzini edirik. x 2 + x -2 = y 2 – 2 ifadələrini əvəz etdikdən sonra;

x 3 + x -3 = y 3 – 3y; x 4 + x -4 = y 4 – 4y + 2 üçün tənliyi alırıq saat Au n + By n -1 +Cy n -2 + … + Ey + D = 0.

Bu tənliyi həll etmək üçün x + x -1 = y k şəklində olan bir neçə kvadrat tənliyi həll etmək lazımdır, burada k = 1, 2, ... n. Beləliklə, orijinal tənliyin köklərini əldə edirik.

Misal 1. x 7 + x 6 – 5x 5 – 13x 4 – 13x 3 – 5x 2 + 2x + 1 = 0 tənliyini həll edin.

Həll. x = – 1 tənliyin köküdür. Horner sxemini tətbiq edək.

Tənliyimiz formanı alacaq:

(x + 1)(x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1) = 0

1) x + 1 = 0, x = -1;

2) x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1 = 0 | : x 3  0; x 3 + x 2 – 6x – 7 – 6/x + 1/x 2 + 1/x 3 =0.

Qruplaşdıraraq əldə edirik: .

Bir əvəz təqdim edək:
;
;
.

Nisbətən alırıq saat tənlik: y 3 – 3y + y 2 – 2 – 6y – 7 = 0;

y 3 + y 2 – 9y – 9 = 0; y 2 (y + 1) – 9 (y + 1) = 0; (y + 1)(y 2 – 9); y 1 = -1, y 2,3 =  3.

Tənliklərin həlli
,
,
,

kökləri alırıq:
,
,
,

Cavab: x 1 = -1,
,

Məşqlər

Tənlikləri həll edin.

2x 5 + 5x 4 – 13x 3 – 13x 2 + 5x + 2 = 0;

2x 4 + 3x 3 – 16x 2 + 3x + 2 = 0;

15x 5 + 34x 4 + 15x 3 – 15x 2 – 34x – 15 = 0.

1.3. Tənliklərin həlli üçün dəyişənlərin dəyişdirilməsi üsulu

Dəyişən dəyişdirmə üsulu ən çox yayılmış üsuldur. Dəyişən dəyişiklik etmək sənəti, hansı dəyişikliyin ən mənalı olduğunu və daha tez uğura aparacağını görməkdir.

Tənlik verilirsə

F(f(x)) = 0, (1)

sonra naməlum y = f (x) əvəz edilərək əvvəlcə tənliyə endirilir

F(y) = 0, (2)

və sonra (2) y 1, y 2, ..., y n, ... tənliyinin bütün həll yollarını tapdıqdan sonra f (x) = y 1, f (x) = y 2 tənliklər çoxluğunun həllinə endirilir. ,..., f (x) = y 2,...

Dəyişən dəyişdirmə metodunun həyata keçirilməsinin əsas yolları bunlardır:

kəsrin əsas xassəsindən istifadə etməklə;

binomialın kvadratını vurğulamaq;

tənliklər sisteminə keçid;

mötərizələri cüt-cüt açmaq;

mötərizələrin cüt-cüt açılması və tənliyin hər iki tərəfinin bölünməsi;

tənliyin dərəcəsini azaltmaq;

ikiqat əvəz.

1.3.1. Tənliyin gücünün azaldılması

(x 2 + x + 2)(x 2 + x + 3) = 6 (3) tənliyini həll edin

Həll. x 2 + x + 2 = y işarəsi verək, sonra y(y+1) = 6 götürək, sonuncunu həll edərək y 1 = 2, y 2 = -3 alırıq. Bu tənlik (3) x 2 + x + 2 = 2 tənliklər toplusuna ekvivalentdir.

x 2 + x + 2 = -3

Birincini həll edərək, x alırıq 1 = 0, x 2 = -1. İkincisini həll edərək, alırıq
,

Cavab: x 1 = 0, x 2 = -1,

1.3.2. (x + a) (x +) formasının dördüncü dərəcəli tənliyib )(x + c )(x + d ) = m , burada a + b = c + d, və ya a + c = b + d və ya a + d = b + c.

Misal. (x - 1)(x - 7)(x -4)(x + 2) = 40 tənliyini həll edin

Həll. – 1- 4 = - 7 + 2, - 5 = - 5, bu mötərizə cütlərini vuraraq (x 2 - 5x - 14)(x 2 - 5x + 4) = 40 tənliyini alırıq.

Əvəzetməni təqdim edək: x 2 - 5x – 14 = y, y(y + 18) = 40, y 2 + 18y = 40, y 2 + 18y – 40 = 0 tənliyini alırıq. y 1 = -20, y 2 = 2. Orijinal dəyişənə qayıdaraq, bir sıra tənlikləri həll edirik:

X 2 - 5x – 14 = - 20 x 1 = 2; x 2 = 3

x 2 - 5x – 14 = 2 x 3.4 =

Cavab: x 1 = 2; x 2 = 3 x 3.4 =

1.3.3. (x + a)(x + b)(x + c)(x + d) = Ex 2 formasının tənliyi,

Harada ab = cd, ya ac =bd, ya da ad = bc. Mötərizələri cüt-cüt açın və hər iki hissəni x 2  0-a bölün.

Misal. (x - 1)(x - 2)(x - 8)(x - 4) = 4x 2

Həll. Birinci və üçüncü və ikinci və dördüncü mötərizədə olan ədədlərin hasili bərabərdir, yəni. – 8 (- 1) = (- 2)(- 4). Göstərilən mötərizə cütlərini çoxaldaq və (x 2 - 9x + 8)(x 2 - 6x + 8) = 4x 2 tənliyini yazaq.

x = 0 tənliyin kökü olmadığı üçün tənliyin hər iki tərəfini x-ə bölürük 2  0, alırıq:
, yerdəyişmə:
, orijinal tənlik aşağıdakı formanı alacaq:t(t+3) =4, t 2 + 3 t=4, t 2 + 3 t – 4=0, t 1 =1, t 2 = - 4.

Orijinal dəyişənə qayıdaq:

x 2 - 10x + 8 = 0

x 2 - 5x + 8 = 0

Birinci tənliyi həll edirik, x alırıq 1,2 = 5 

İkinci tənliyin kökləri yoxdur.

Cavab: x 1,2 = 5 

1.3.4. Dördüncü növ tənlik (ax 2 + b 1 x + c)(a x 2 + b 2 x + c) = A x 2

Tənlik (balta 2 + b 1 x+ c)(a x 2 + b 2 x + c) = A x 2, burada c  0, A  2
, naməlumu əvəz etdikdən sonra
kvadrat şəklində yenidən yazıla bilər və asanlıqla həll edilə bilər.

Misal. (x 2 + x+ 2)(x 2 + 2x + 2) = 2x 2

Həll. Bu tənliyi x-ə bölməklə x = 0-ın bu tənliyin kökü olmadığını görmək asandır. 2 , tənliyini alırıq

yerdəyişmə
, (y+1)(y+2) = 2 tənliyini alırıq, onu həll edirik, y köklərimiz var 1 = 0; 2-də = - 3, buna görə də ilkin tənlik tənliklər çoxluğuna bərabərdir

həll edərək, x 1 = -1 alırıq; x 2 = -2.

Cavab: x 1 = -1; x 2 = -2

1.3.5. Formanın tənliyi: a (cx 2 + p 1 x + q) 2 + b (cx 2 + p 2 x + q) 2 = Ax 2

tənlik a(cx 2 + səh 1 x + q) 2 + b(cx 2 + səh 2 x + q) 2 = balta 2 harada a, b, c, q, A belədirlər q 0, A 0, c 0, a 0, b 0-ın x = 0 kökü yoxdur, ona görə də tənliyi x-ə bölmək 2 , ekvivalent tənlik əldə edirik
, dəyişdirildikdən sonra
şəklində yenidən yazılacaq kvadrat tənlik, bu asanlıqla həll olunur. + 1)( x 2 – 14x + 15 = 0

x 2 – 7 x + 15 = 0

Cavab:

Fizikanın bəzi problemlərində prosesi təsvir edən kəmiyyətlər arasında birbaşa əlaqə yaratmaq mümkün deyil. Lakin tədqiq olunan funksiyaların törəmələrini ehtiva edən bərabərlik əldə etmək mümkündür. Diferensial tənliklər belə yaranır və naməlum funksiyanı tapmaq üçün onları həll etmək zərurəti yaranır.

Bu məqalə naməlum funksiyanın bir dəyişənin funksiyası olduğu diferensial tənliyin həlli problemi ilə üzləşənlər üçün nəzərdə tutulub. Nəzəriyyə elə qurulmuşdur ki, diferensial tənliklər haqqında sıfır biliyə malik olmaqla siz öz tapşırığınızın öhdəsindən gələ bilərsiniz.

Diferensial tənliyin hər bir növü tipik misal və problemlərin ətraflı izahı və həlli ilə həll üsulu ilə əlaqələndirilir. Sadəcə probleminizin diferensial tənliyinin növünü müəyyən etmək, təhlil edilən oxşar nümunə tapmaq və oxşar hərəkətləri yerinə yetirmək kifayətdir.

Diferensial tənlikləri uğurla həll etmək üçün sizə antiderivativlər çoxluqlarını tapmaq bacarığı da lazımdır ( qeyri-müəyyən inteqrallar) müxtəlif funksiyalar. Lazım gələrsə, bölməyə müraciət etməyi məsləhət görürük.

Əvvəlcə törəmə ilə bağlı həll edilə bilən birinci dərəcəli adi diferensial tənliklərin növlərini nəzərdən keçirəcəyik, sonra ikinci dərəcəli ODE-lərə keçəcəyik, daha sonra daha yüksək dərəcəli tənliklər üzərində dayanacağıq və sistemləri ilə bitirəcəyik. diferensial tənliklər.

Xatırladaq ki, əgər y x arqumentinin funksiyasıdırsa.

Birinci dərəcəli diferensial tənliklər.

Formanın ən sadə birinci dərəcəli diferensial tənlikləri.

Belə uzaqdan idarəetmənin bir neçə nümunəsini yazaq .

Diferensial tənliklər bərabərliyin hər iki tərəfini f(x) -ə bölməklə törəmə ilə bağlı həll etmək olar. Bu halda f(x) ≠ 0 üçün ilkin tənliyə ekvivalent olacaq tənliyə çatırıq. Bu cür ODE-lərə misal ola bilər.

Əgər f(x) və g(x) funksiyalarının eyni vaxtda itdiyi x arqumentinin qiymətləri varsa, əlavə həllər yaranır. Tənliyə əlavə həllər verilmiş x bu arqument qiymətləri üçün müəyyən edilmiş istənilən funksiyalardır. Belə diferensial tənliklərə misal olaraq:

İkinci dərəcəli diferensial tənliklər.

Sabit əmsallı ikinci dərəcəli xətti homogen diferensial tənliklər.

Sabit əmsallı LDE çox yayılmış diferensial tənlik növüdür. Onların həlli xüsusilə çətin deyil. Əvvəlcə xarakterik tənliyin kökləri tapılır . Müxtəlif p və q üçün üç hal mümkündür: xarakterik tənliyin kökləri həqiqi və fərqli, həqiqi və üst-üstə düşə bilər. və ya mürəkkəb birləşmələr. Xarakterik tənliyin köklərinin dəyərlərindən asılı olaraq yazılır ümumi qərar kimi diferensial tənlik , və ya , və ya müvafiq olaraq.

Məsələn, xətti homojeni nəzərdən keçirək diferensial tənlik sabit əmsallı ikinci sıra. Onun xarakterik tənliyinin kökləri k 1 = -3 və k 2 = 0-dır. Köklər həqiqi və fərqlidir, buna görə də sabit əmsallı LODE-nin ümumi həlli formaya malikdir


Sabit əmsallı ikinci dərəcəli xətti qeyri-bərabər diferensial tənliklər.

Sabit əmsalları y olan ikinci dərəcəli LDDE-nin ümumi həlli müvafiq LDDE-nin ümumi həllinin cəmi şəklində axtarılır. və orijinal qeyri-homogen tənliyin xüsusi həlli, yəni . Əvvəlki paraqraf sabit əmsallı homojen diferensial tənliyin ümumi həllinin tapılmasına həsr edilmişdir. Və müəyyən bir həll ya metodla müəyyən edilir qeyri-müəyyən əmsallar f(x) funksiyasının müəyyən forması üçün ilkin tənliyin sağ tərəfində və ya ixtiyari sabitləri dəyişmək üsulu ilə.

Sabit əmsalları olan ikinci dərəcəli LDDE-lərə misal olaraq veririk


Nəzəriyyəni anlayın və onunla tanış olun ətraflı həllər Sizə sabit əmsallı ikinci dərəcəli xətti qeyri-bərabər diferensial tənliklər səhifəsində nümunələr təqdim edirik.

Xətti homojen diferensial tənliklər (LODE) və ikinci dərəcəli xətti qeyri-homogen diferensial tənliklər (LNDE).

Bu tip diferensial tənliklərin xüsusi halı sabit əmsallı LODE və LDDE-dir.

Müəyyən bir seqmentdə LODE-nin ümumi həlli bu tənliyin iki xətti müstəqil qismən y 1 və y 2 həllinin xətti birləşməsi ilə təmsil olunur, yəni, .

Əsas çətinlik bu tip diferensial tənliyə xətti müstəqil qismən həllər tapmaqdadır. Tipik olaraq, xüsusi həllər aşağıdakı xətti müstəqil funksiyalar sistemlərindən seçilir:


Bununla belə, xüsusi həllər həmişə bu formada təqdim edilmir.

LOD nümunəsidir .

LDDE-nin ümumi həlli formada axtarılır, burada müvafiq LDDE-nin ümumi həlli və orijinal diferensial tənliyin xüsusi həllidir. Biz bayaq onu tapmaq haqqında danışdıq, lakin onu ixtiyari sabitlərin dəyişdirilməsi metodundan istifadə etməklə müəyyən etmək olar.

LNDU-nu misal göstərmək olar .

Daha yüksək dərəcəli diferensial tənliklər.

Sıra ilə azalmaya imkan verən diferensial tənliklər.

Diferensial tənliyin sırası k-1 sırasına qədər istənilən funksiyanı və onun törəmələrini ehtiva etməyən , əvəz etməklə n-k-ə endirilə bilər.

Bu halda, orijinal diferensial tənlik -ə endiriləcəkdir. Onun həlli p(x) tapıldıqdan sonra əvəzlənməyə qayıtmaq və naməlum y funksiyasını təyin etmək qalır.

Məsələn, diferensial tənlik dəyişdirildikdən sonra o, ayrıla bilən dəyişənlərə malik tənliyə çevriləcək və onun sırası üçüncüdən birinciyə endiriləcək.