Koliki je zbir uglova? Teorema o zbiru uglova trougla. Vrste prema veličini ugla

Zbir uglova trougla- važno, ali dovoljno jednostavna tema, koji se uči u 7. razredu geometrije. Tema se sastoji od teoreme, kratkog dokaza i nekoliko logičkih posljedica. Poznavanje ove teme pomaže u rješavanju geometrijski problemi tokom naknadnog proučavanja predmeta.

Teorema - koji su uglovi proizvoljnog trougla sabrani?

Teorema kaže da ako uzmete bilo koji trougao, bez obzira na njegovu vrstu, zbir svih uglova će uvijek biti 180 stepeni. To se dokazuje na sljedeći način:

• na primjer, uzmite trokut ABC, povucite ravnu liniju kroz tačku B koja se nalazi na vrhu i označite je kao "a", prava linija "a" je strogo paralelna sa stranicom AC;
• između prave "a" i stranica AB i BC označeni su uglovi, koji su označeni brojevima 1 i 2;
• ugao 1 se smatra jednakim kutu A, a ugao 2 jednak kutu C, jer se smatra da ovi uglovi leže poprečno;
• dakle, zbir između uglova 1, 2 i 3 (koji je označen umesto ugla B) se priznaje kao jednak nesavijenom uglu sa vrhom B - i iznosi 180 stepeni.

Ako je zbir uglova označenih brojevima 180 stepeni, tada se zbir uglova A, B i C smatra jednakim 180 stepeni. Ovo pravilo važi za bilo koji trougao.

Ono što slijedi iz geometrijske teoreme

Uobičajeno je istaknuti nekoliko posljedica iz gornje teoreme.

• Ako problem razmatra trougao sa pravim uglom, tada će jedan od njegovih uglova biti po defaultu jednak 90 stepeni, a zbir oštrih uglova će takođe biti 90 stepeni.
• Ako govorimo o pravokutnom jednakokračnom trokutu, tada će njegovi oštri uglovi, koji zajedno iznose 90 stepeni, pojedinačno biti jednaki 45 stepeni.
• Jednakostranični trougao sastoji se od tri jednaka ugla, odnosno svaki od njih će biti jednak 60 stepeni, a ukupno će biti 180 stepeni.
• Vanjski ugao bilo kojeg trokuta bit će jednak zbiru dvaju unutrašnjih ugla koji nisu susjedni njemu.

Može se izvesti sljedeće pravilo: svaki trougao ima najmanje dva oštra ugla. U nekim slučajevima trokut se sastoji od tri oštra ugla, a ako su samo dva, onda će treći ugao biti tup ili pravi.

Teorema. Zbir unutrašnjih uglova trougla jednak je dvama pravim uglovima.

Uzmimo neki trougao ABC (slika 208). Označimo njegove unutrašnje uglove brojevima 1, 2 i 3. Dokažimo to

∠1 + ∠2 + ∠3 = 180°.

Provucimo kroz neki vrh trougla, na primjer B, pravu liniju MN paralelnu sa AC.

U vrhu B imamo tri ugla: ∠4, ∠2 i ∠5. Njihov zbir je pravi ugao, pa je jednak 180°:

∠4 + ∠2 + ∠5 = 180°.

Ali ∠4 = ∠1 su unutrašnji poprečni uglovi sa paralelnim linijama MN i AC i sekantom AB.

∠5 = ∠3 - ovo su unutrašnji poprečni uglovi sa paralelnim linijama MN i AC i sekantom BC.

To znači da ∠4 i ∠5 mogu biti zamijenjeni njihovim jednakima ∠1 i ∠3.

Dakle, ∠1 + ∠2 + ∠3 = 180°. Teorema je dokazana.

2. Svojstvo vanjskog ugla trougla.

U stvari, u trouglu ABC (slika 209) ∠1 + ∠2 = 180° - ∠3, ali i ∠VSD, spoljni ugao ovog trougla, koji nije susedan sa ∠1 i ∠2, takođe je jednak 180° - ∠3 .

ovako:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Dakle, ∠1 + ∠2= ∠BCD.

Izvedeno svojstvo spoljašnjeg ugla trougla pojašnjava sadržaj prethodno dokazane teoreme o spoljašnjem uglu trougla, koja je samo govorila da je spoljašnji ugao trougla veći od svakog unutrašnjeg ugla trougla koji mu nije susedan; sada je utvrđeno da je vanjski ugao jednak zbiru oba unutrašnja ugla koja mu ne graniče.

3. Svojstvo pravouglog trougla sa uglom od 30°.

Neka je ugao B u pravouglom trouglu ACB jednak 30° (Sl. 210). Tada će njegov drugi oštri ugao biti jednak 60°.

Dokažimo da je krak AC jednak polovini hipotenuze AB. Produžimo krak AC izvan vrha pravog ugla C i odvojimo segment CM jednak segmentu AC. Povežimo tačku M sa tačkom B. Dobijeni trougao VSM jednak je trouglu ACB. Vidimo da je svaki ugao trougla ABM jednak 60°, stoga je ovaj trougao jednakostraničan trougao.

krak AC jednak je polovini AM, a pošto je AM jednak AB, krak AC će biti jednak polovini hipotenuze AB.

Zbir unutrašnjih uglova trougla je 180 0. Ovo je jedan od osnovnih aksioma Euklidove geometrije. Ovo je geometrija koju uče školarci. Geometrija se definiše kao nauka koja proučava prostorne oblike stvarnog sveta.

Šta je motivisalo stare Grke da razviju geometriju? Potreba za mjerenjem njiva, livada - površina zemljine površine. U isto vrijeme, stari Grci su prihvatili da je površina Zemlje horizontalna i ravna. Uzimajući u obzir ovu pretpostavku, stvoreni su Euklidovi aksiomi, uključujući zbir unutrašnjih uglova trokuta od 180 0.

Aksiom je tvrdnja koja ne zahtijeva dokaz. Kako ovo treba shvatiti? Izražava se želja koja odgovara osobi, a zatim se potvrđuje ilustracijama. Ali sve što nije dokazano je fikcija, nešto što ne postoji u stvarnosti.

Uzimajući zemljinu površinu horizontalno, stari Grci su automatski prihvatili oblik Zemlje kao ravan, ali je drugačiji – sferičan. U prirodi uopšte ne postoje horizontalne ravni ili prave linije, jer gravitacija savija prostor. Prave linije i horizontalne ravni nalaze se samo u ljudskom mozgu.

Stoga je Euklidova geometrija, koja objašnjava prostorne forme fiktivnog svijeta, simulakrum – kopija koja nema original.

Jedan od Euklidovih aksioma kaže da je zbir unutrašnjih uglova trougla 180 0. Zapravo, u stvarnom zakrivljenom prostoru, ili na sfernoj površini Zemlje, zbir unutrašnjih uglova trougla je uvek veći od 180 0.

Hajde da razmišljamo ovako. Bilo koji meridijan na globusu seče sa ekvatorom pod uglom od 90 0. Da biste dobili trougao, morate odmaknuti još jedan meridijan od meridijana. Zbir uglova trokuta između meridijana i strane ekvatora biće 180 0. Ali i dalje će postojati ugao na polu. Kao rezultat, zbir svih uglova će biti veći od 180 0.

Ako se stranice sijeku pod uglom od 90 0 na polu, tada će zbir unutrašnjih uglova takvog trougla biti 270 0. Dva meridijana koji sijeku ekvator pod pravim uglom u ovom trouglu bit će paralelni jedan s drugim, a na polu koji se sijeku jedan drugog pod uglom od 90 0 postat će okomite. Ispostavilo se da dvije paralelne prave na istoj ravni ne samo da se sijeku, već mogu biti i okomite na pol.

Naravno, stranice takvog trokuta neće biti ravne linije, već konveksne, ponavljajući sferni oblik globus. Ali ovo je upravo stvarni svijet svemira.

Geometrija realnog prostora, uzimajući u obzir njegovu zakrivljenost sredinom 19. stoljeća. razvio njemački matematičar B. Riemann (1820-1866). Ali školarcima se o tome ne govori.

Dakle, euklidska geometrija, koja ima oblik Zemlje kao ravne sa horizontalnom površinom, što u stvari nije, je simulakrum. Nootic je Rimanova geometrija koja uzima u obzir zakrivljenost prostora. Zbir unutrašnjih uglova trokuta u njemu veći je od 180 0.

Dokaz

Neka ABC" - proizvoljan trougao. Hajdemo kroz vrh B linija paralelna sa linijom A.C. (takva prava linija se zove euklidska prava linija). Hajde da označimo tačku na tome D tako da tačke A I D ležati na suprotnim stranama prave linije B.C..Uglovi DBC I ACB jednak kao unutrašnji poprečno ležeći formiran sekantom B.C. sa paralelnim linijama A.C. I BD. Dakle, zbir uglova trougla na vrhovima B I WITH jednaka uglu ABD.Zbir sva tri ugla trougla jednak je zbiru uglova ABD I BAC. Pošto su ovi uglovi unutrašnji jednostrani za paralelu A.C. I BD na secantu AB, tada je njihov zbir 180°. Teorema je dokazana.

Posljedice

Iz teoreme slijedi da svaki trougao ima dva oštra ugla. Zaista, koristeći dokaz kontradikcijom, pretpostavimo da trokut ima samo jedan oštar ugao ili uopće nema oštar ugl. Tada ovaj trougao ima najmanje dva ugla, od kojih je svaki najmanje 90°. Zbir ovih uglova nije manji od 180°. Ali to je nemoguće, jer je zbir svih uglova trougla 180°. Q.E.D.

Generalizacija u simpleks teoriju

Gdje je ugao između i i j strana simpleksa.

Bilješke

• Na sferi, zbir uglova trokuta uvek prelazi 180°, razlika se naziva sferni višak i proporcionalna je površini trokuta.
• U ravni Lobačevskog, zbir uglova trougla je uvek manji od 180°. Razlika je također proporcionalna površini trokuta.

vidi takođe

Wikimedia Foundation. 2010.

Pogledajte šta je "Teorema o zbiru uglova trougla" u drugim rečnicima:

Svojstvo poligona u euklidskoj geometriji: Zbir uglova n trougla je 180°(n 2). Sadržaj 1 Dokaz 2 Napomena ... Wikipedia

Pitagorina teorema je jedna od temeljnih teorema euklidske geometrije, koja uspostavlja odnos između stranica pravokutnog trougla. Sadržaj 1 ... Wikipedia

Pitagorina teorema je jedna od temeljnih teorema euklidske geometrije, koja uspostavlja odnos između stranica pravokutnog trougla. Sadržaj 1 Izjave 2 Dokazi ... Wikipedia

Kosinusna teorema je generalizacija Pitagorine teoreme. Kvadrat stranice trokuta jednak je zbiru kvadrata njegove dvije druge strane bez dvostrukog umnožaka ovih stranica na kosinus ugla između njih. Za ravan trougao sa strane a,b,c i ugao α... ... Wikipedia

Ovaj izraz ima druga značenja, pogledajte Trougao (značenja). Trougao (u Euklidskom prostoru) je geometrijska figura, formirana od tri segmenta koji spajaju tri tačke koje ne leže na istoj pravoj liniji. Tri tačke,... ... Wikipedia

Standardna notacija Trougao je najjednostavniji poligon koji ima 3 vrha (ugla) i 3 strane; dio ravni omeđen sa tri tačke koje ne leže na istoj pravoj i tri segmenta koji povezuju ove tačke u paru. Vrhovi trougla ... Wikipedia

starogrčki matematičar. Djelovao u Aleksandriji u 3. vijeku. BC e. Glavno djelo “Principia” (15 knjiga), koje sadrži osnove antičke matematike, elementarne geometrije, teorije brojeva, opšta teorija odnosi i metode za određivanje površina i zapremina, ... ... enciklopedijski rječnik

- (umro između 275. i 270. pne) starogrčki matematičar. Podaci o vremenu i mestu njegovog rođenja nisu stigli do nas, ali se zna da je Euklid živeo u Aleksandriji i da je vrhunac njegove delatnosti nastupio za vreme vladavine Ptolomeja I u Egiptu... Veliki enciklopedijski rječnik

Geometrija je slična euklidskoj geometriji po tome što definira kretanje figura, ali se razlikuje od euklidske geometrije po tome što je jedan od njenih pet postulata (drugi ili peti) zamijenjen njegovom negacijom. Negacija jednog od euklidskih postulata ... ... Collier's Encyclopedia

Trougao . Oštar, tupougli i pravougaoni trokut.

Noge i hipotenuza. Jednakokraki i jednakostranični trokut.

Zbir uglova trougla.

Vanjski ugao trougla. Znakovi jednakosti trouglova.

Izvanredne linije i tačke u trokutu: visine, medijane,

simetrale, medijana e okomice, ortocentar,

centar gravitacije, centar opisane kružnice, centar upisane kružnice.

Pitagorina teorema. Omjer stranica u proizvoljnom trouglu.

Trougao je poligon sa tri strane (ili tri ugla). Stranice trougla su često označene malim slovima koji odgovaraju velikim slovima koji predstavljaju suprotne vrhove.

Ako su sva tri ugla oštra (slika 20), onda ovo oštar trougao . Ako je jedan od uglova pravi(C, sl.21), to je pravougaonog trougla; stranea, bkoji formiraju pravi ugao nazivaju se noge; stranacnasuprot pravog ugla se zove hipotenuza. Ako jedan od tupi uglovi (B, sl. 22), to je tupougaonog trougla.


Trougao ABC (sl. 23) - jednakokraki, Ako dva njegove strane su jednake (a= c); ove jednake strane se nazivaju bočno, poziva se treća strana osnovu trougao. Trougao ABC (Sl. 24) – equilateral, Ako Sve njegove strane su jednake (a = b = c). Uglavnom ( a ≠ b ≠ c) imamo scalene trougao .

Osnovna svojstva trouglova. U bilo kom trouglu:

1. Nasuprot veće strane leži veći ugao, i obrnuto.

2. Jednaki uglovi leže nasuprot jednakih strana, i obrnuto.

Konkretno, svi uglovi unutra equilateral trouglovi su jednaki.

3. Zbir uglova trougla je 180 º .

Iz posljednja dva svojstva slijedi da je svaki ugao u jednakostranični

trougao je 60 º.

4. Nastavljajući jednu od stranica trougla (AC, sl. 25), dobijamo vanjski

ugao BCD . Vanjski ugao trougla jednak je zbiru unutrašnjih uglova,

nije u blizini : BCD = A + B.

5. Bilo koji stranica trougla manja je od zbira druge dvije stranice i veća

njihove razlike (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Znakovi jednakosti trouglova.

Trokuti su podudarni ako su respektivno jednaki:

a ) dvije stranice i ugao između njih;

b ) dva ugla i strana uz njih;

c) tri strane.

Znaci jednakosti pravokutnih trougla.

Dva pravougaona trokuti su jednaki ako je ispunjen jedan od sljedećih uslova:

1) noge su im jednake;

2) kateta i hipotenuza jednog trougla jednake su kateta i hipotenuze drugog trougla;

3) hipotenuza i oštar ugao jednog trougla jednaki su hipotenuzi i oštrom uglu drugog trougla;

4) kateta i susedni oštar ugao jednog trougla jednaki su kateta i susednom oštrom uglu drugog trougla;

5) kateta i suprotni oštar ugao jednog trougla jednaki su kateta i suprotan oštri ugao drugog.

Divne linije i tačke u trouglu.

Visina trougao jeokomito,spušten sa bilo kojeg vrha na suprotnu stranu ( ili njegov nastavak). Ova strana se zoveosnovicu trougla . Tri visine trougla se uvek sekuu jednom trenutku, zvao ortocentar trougao. Ortocentar oštrog trougla (tačka O , sl. 26) nalazi se unutar trougla, iortocentar tupouglog trougla (tačka O , sl.27) – vani; Ortocentar pravouglog trougla poklapa se sa vrhom pravog ugla.

Medijan - Ovo linijski segment , povezuje bilo koji vrh trokuta sa sredinom suprotne strane. Tri medijane trougla (AD, BE, CF, sl. 28) seku u jednoj tački O , uvijek leži unutar trougla i biti njegov centar gravitacije. Ova tačka dijeli svaku medijanu u omjeru 2:1, računajući od temena.

Simetrala - Ovo segment simetrale ugao od temena do tačke raskrsnice sa suprotnom stranom. Tri simetrale trougla (AD, BE, CF, sl. 29) seku u jednoj tački Oh, uvek leži unutar trougla I biće centar upisane kružnice(vidi odjeljak „Upisanoi opisani poligoni").

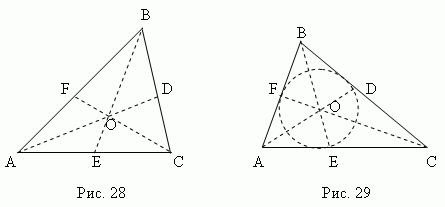
Simetrala dijeli suprotnu stranu na dijelove proporcionalne susjednim stranicama ; na primjer, na slici 29 AE: CE = AB: BC.

Srednja okomita je okomica povučena iz sredine segmentne tačke (strane). Tri okomite simetrale trougla ABC(KO, MO, NE, sl. 30 ) seku u jednoj tački O, što je centar opisan krug (tačke K, M, N – sredine stranica trougla ABC).

U oštrom trouglu, ova tačka leži unutar trougla; u tupim - spolja; u pravougaoniku - u sredini hipotenuze. Ortocentar, centar gravitacije, centar opisanog i upisana kružnica poklapaju samo u jednakostraničnom trouglu.

Pitagorina teorema. U pravokutnom trokutu, kvadrat dužineHipotenuza je jednaka zbroju kvadrata dužina kateta.

Dokaz Pitagorine teoreme jasno slijedi sa slike 31. Razmotrimo pravougli trougao ABC sa nogama a, b i hipotenuzu c.

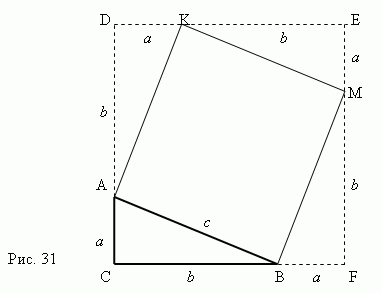
Hajde da napravimo kvadrat AKMB koristeći hipotenuzu AB kao stranu. Ondanastaviti stranice pravouglog trougla ABC tako da se dobije kvadrat CDEF , čija je strana jednakaa + b .Sada je jasno da je površina kvadrata CDEF je jednak ( a+b) 2 . S druge strane, ovo površina je jednaka zbiru oblasti četiri pravougla trougla i kvadrat AKMB tj

c 2 + 4 (ab / 2) = c 2 + 2 ab,

odavde,

c 2 + 2 ab= (a+b) 2 ,

i konačno imamo:

c 2 =a 2 +b 2 .

Omjer stranica u proizvoljnom trouglu.

U opštem slučaju (za proizvoljan trougao) imamo:

c 2 =a 2 +b 2 – 2ab· cos C,

gdje je C – ugao između stranicaa I b .