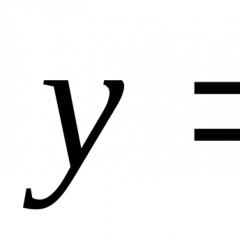Višedimenzionalni Markovljevi procesi. Metode teorije Markovljevih procesa. Diskretni Markovi lanci. Primjer

Mnoge operacije koje je potrebno analizirati pri izboru optimalnog rješenja razvijaju se kao slučajni procesi u zavisnosti od niza slučajnih faktora.

Za matematički opis mnogih operacija koje se razvijaju u obliku slučajnog procesa, može se uspješno primijeniti matematički aparat razvijen u teoriji vjerovatnoće za takozvane Markovljeve slučajne procese.

Objasnimo koncept Markovljevog slučajnog procesa.

Neka postoji neki sistem S,čije se stanje mijenja tokom vremena (pod sistemom S može značiti bilo šta: industrijsko preduzeće, tehnički uređaj, servisna radionica itd.). Ako stanje sistema S mijenja se tokom vremena na nasumičan, unaprijed nepredvidiv način, to kažu u sistemu S curenja slučajni proces.

Primjeri nasumičnih procesa:

fluktuacije cijena na berzi;

služba za korisnike u frizerskom salonu ili radionici za popravke;

implementacija plana nabavke za grupu preduzeća itd.

Specifičan tok svakog od ovih procesa zavisi od niza nasumičnih, prethodno nepredvidivih faktora, kao što su:

dolazak nepredvidivih vijesti o političkim promjenama na berzi;

slučajna priroda toka aplikacija (zahtjeva) koje dolaze od klijenata;

slučajni prekidi u realizaciji plana snabdevanja itd.

DEFINICIJA. Nasumični proces koji se odvija u sistemu se zove Markovian(ili proces bez posledica), ako ima sljedeće svojstvo: za svaki trenutak vremena t 0 vjerovatnoća bilo kojeg stanja sistema u budućnosti (s t > t 0) zavisi samo od njegovog stanja u sadašnjosti (s t = t 0) i ne zavisi od toga kada i kako je sistem došao u ovo stanje (tj. kako se proces razvijao u prošlosti).

Drugim riječima, u Markovljevom slučajnom procesu, njegov budući razvoj zavisi samo od sadašnjeg stanja i ne zavisi od „predistorije“ procesa.

Pogledajmo primjer. Pustite sistem S predstavlja berzu koja postoji već neko vrijeme. Zanima nas kako će sistem funkcionirati u budućnosti. Jasno je, barem u prvoj aproksimaciji, da karakteristike budućeg učinka (vjerovatnosti pada cijene određene dionice u sedmici) zavise od stanja sistema u ovom trenutku (različiti faktori kao što su jer odluke vlade ili izborni rezultati mogu intervenirati ovdje) i ne zavise od toga kada i kako je sistem dostigao svoje trenutno stanje (ne zavisi od prirode kretanja cijena ovih dionica u prošlosti).

U praksi se često susrećemo sa slučajnim procesima koji se, do različitog stepena aproksimacije, mogu smatrati markovskim.

Teorija Markovljevih slučajnih procesa ima širok raspon različitih primjena. Uglavnom će nas zanimati primjena teorije Markovljevih slučajnih procesa na konstrukciju matematičkih modela operacija čiji tok i ishod značajno zavise od slučajnih faktora.

Markovljevi slučajni procesi se dijele na casovi u zavisnosti od toga kako i u kom trenutku sistem S" može promijeniti svoja stanja.

DEFINICIJA. Nasumični proces se zove proces sa diskretnim stanjima, ako je moguće stanja sistema s x , s 2 , s v... mogu se popisivati (numerisati) jedan za drugim, a sam proces je da s vremena na vrijeme sistem S skače naglo (trenutačno) iz jednog stanja u drugo.

Na primjer, razvoj projekta S provode zajedno dva odjela, od kojih svako može pogriješiti. Moguća su sljedeća stanja sistema:

5, - oba odjela rade normalno;

s 2 - prvi odjel je napravio grešku, drugi radi dobro;

s 3 - drugi odjel je napravio grešku, prvi radi dobro;

s 4 - oba odjela su pogriješila.

Proces koji se odvija u sistemu je da se on nasumično u nekim vremenskim momentima kreće („skače“) iz stanja u stanje. Sistem ima ukupno četiri moguća stanja. Pred nama je proces sa diskretnim stanjima.

Pored procesa sa diskretnim stanjima, postoje slučajni procesi sa kontinuiranim stanjima: ove procese karakterizira postepeni, glatki prijelaz iz stanja u stanje. Na primjer, proces promjene napona u rasvjetnoj mreži je slučajan proces sa kontinuiranim stanjima.

Razmotrićemo samo slučajne procese sa diskretnim stanjima.

Kada se analiziraju slučajni procesi sa diskretnim stanjima, vrlo je zgodno koristiti geometrijsku šemu - takozvani graf stanja. Grafikon stanja geometrijski prikazuje moguća stanja sistema i njegove moguće prelaze iz stanja u stanje.

Neka postoji sistem S sa diskretnim stanjima:

Svako stanje će biti predstavljeno pravokutnikom, a mogući prijelazi (“skokovi”) iz stanja u stanje bit će predstavljeni strelicama koje povezuju ove pravokutnike. Primjer grafa stanja prikazan je na Sl. 4.1.

Imajte na umu da strelice označavaju samo direktne prelaze iz stanja u stanje; ako sistem može preći iz stanja s 2 na 5 3 samo kroz s y tada strelice označavaju samo prelaze s 2-> i l, 1 -> 5 3, ali ne s 2 -» s y Pogledajmo nekoliko primjera:

1. Sistem S- kompanija koja može biti u jednom od pet mogućih stanja: s ]- radi sa profitom;

s 2- izgubio izglede za razvoj i prestao da ostvaruje profit;

5 3 - postao objekt za potencijalno preuzimanje;

s 4- je pod eksternom kontrolom;

s 5- imovina likvidiranog preduzeća se prodaje na aukciji.

Grafikon stanja kompanije prikazan je na sl. 4.2.

Rice. 4.2

2. Sistem S- banka sa dvije filijale. Moguća su sljedeća stanja sistema:
5, - obje filijale posluju s dobiti;

s 2 - prva filijala posluje bez dobiti, druga radi sa dobiti;

5 3 - druga filijala posluje bez dobiti, prva posluje sa profitom;

s 4 - obje filijale posluju bez dobiti.

Pretpostavlja se da nema poboljšanja stanja.

Grafikon stanja je prikazan na sl. 4.3. Imajte na umu da grafikon ne prikazuje mogući prijelaz iz stanja s ] direktno na s4,što će se ostvariti ako banka odmah poslovaće sa gubitkom. Mogućnost ovakvog događaja može se zanemariti, što praksa potvrđuje.

Rice. 4.3

3. Sistem S- investiciono društvo koje se sastoji od dva trgovca (odjeljenja): I i II; svaki od njih može u nekom trenutku početi raditi s gubitkom. Ako se to dogodi, menadžment kompanije odmah preduzima mjere za vraćanje profitabilnog rada odjela.

Moguća stanja sistema: s- djelatnosti oba odjela su profitabilne; s 2- prvo odeljenje se obnavlja, drugo radi sa profitom;

s 3- prvo odeljenje radi sa profitom, drugo se obnavlja;

s 4- oba odjela se obnavljaju.

Grafikon stanja sistema prikazan je na Sl. 4.4.

4. U uslovima prethodnog primjera, aktivnosti svakog trgovca, prije nego što počne da obnavlja profitabilan rad odjela, podliježu proučavanju menadžmenta kompanije kako bi se preduzele mjere za njegovo poboljšanje.

Radi pogodnosti, numerisaćemo stanja sistema ne sa jednim, već sa dva indeksa; prvi će značiti status prvog trgovca (1 - radi s profitom, 2 - njegove aktivnosti proučava menadžment, 3 - vraća profitabilnu aktivnost odjela); drugi - iste države za drugog trgovca. Na primjer, s 23 značiće: proučavaju se aktivnosti prvog trgovca, drugog vraća profitabilan rad.

Moguća stanja sistema S:

s u- aktivnosti oba trgovca donose profit;

s l2- prvi trgovac radi sa profitom, aktivnosti drugog proučava menadžment kompanije;

5 13 - prvi trgovac radi sa profitom, drugi obnavlja profitabilnu aktivnost odjela;

s 2l- aktivnosti prvog trgovca proučava menadžment, drugog radi sa profitom;

s 22 - aktivnosti oba trgovca proučava menadžment;

5 23 - proučava se rad prvog trgovca, drugi trgovac obnavlja profitabilne aktivnosti odjela;
5 31 - prvi trgovac obnavlja profitabilne aktivnosti odjela, drugi radi s profitom;
5 32 - prvi trgovac obnavlja profitabilnu aktivnost odjela, proučava se rad drugog trgovca;
5 33 - oba trgovca obnavljaju profitabilan rad svog odjela.

Ukupno ima devet država. Grafikon stanja je prikazan na sl. 4.5.

Iz definicije Markovljevog procesa date u odjeljku 5.1.6, kao i direktno iz formule (5.6), slijedi

Uslovna gustina

naziva se gustina vjerovatnoće prijelaza Markovljevog procesa iz stanja y u trenutku s u stanje x u trenutku t.

Koristeći formulu (2.57), određujemo višedimenzionalnu gustinu vjerovatnoće (bilo kojeg konačnog reda) Markovljevog procesa

Formula (5.60) znači faktorizaciju višedimenzionalne gustine vjerovatnoće Markovljevog procesa – njenu reprezentaciju kao proizvod jednodimenzionalne gustine i gustine prijelazne vjerovatnoće. Uslov faktorizacije (5.60) višedimenzionalne gustine je karakteristična karakteristika Markovljevih procesa (uporedi sa sličnim jednostavnijim uslovom faktorizacije (5.4) za procese sa nezavisnim vrednostima).

Jednodimenzionalna gustina i gustina verovatnoće prelaza su povezane relacijom

Gustoća vjerovatnoće prijelaza Markovljevog procesa nije proizvoljna uslovna funkcija raspodjele koja zadovoljava samo uobičajene uslove nenegativnosti i normalizacije, tj. Takođe mora zadovoljiti neku integralnu jednačinu. Zaista, iz (5.60) u imamo

Integrirajući obje strane ove jednakosti preko , Dobijamo

i od tada

Integralna jednačina (5.62) naziva se Kolmogorov-Chapmanova jednačina.

5.4.2. Homogeni Markovljevi procesi.

Ako je raspodjela vjerovatnoće Markovljevog procesa invarijantna na vremenski pomak, onda se naziva homogena (stacionarna). U ovom slučaju, gustina vjerovatnoće prijelaza (5.59) ovisi samo o jednom vremenskom parametru.

Uslov faktorizacije za višedimenzionalnu gustinu homogenog Markovljevog procesa zapisuje se u obliku) [vidi (5.60)]

Imajte na umu da se klasa homogenih Markovljevih procesa poklapa sa razmatranom klasom homogenih slučajnih procesa sa nezavisnim inkrementima.

5.4.3. Višestruko povezani Markovljev proces.

Markovljev proces nazivamo povezanim ako gustina vjerovatnoće prijelaza ovisi o k prethodnih vrijednosti procesa [vidi (5.58)]:

Uslov faktorizacije za višedimenzionalnu gustinu povezanog Markovljevog procesa zapisuje se kao

i Kolmogorov-Chapman jednadžba

5.4.4. Vektorski Markov proces.

Skup slučajnih procesa formira vektorski Markovljev proces ako je za potpuni probabilistički opis ovog skupa potrebno i dovoljno znati zajedničku distribuciju

i uslovnu distribuciju

ili odgovarajuću gustinu vjerovatnoće prijelaza

Zamjenom - (5.62) skalarnih veličina vektorskim, dobijamo odgovarajuće relacije za vektorski Markovljev proces.

Svaki od slučajnih procesa koji pripadaju skupu koji formira vektorski Markovljev proces naziva se komponentom vektorskog Markovljevog procesa, koji, međutim, nije skalarni Markovljev proces, općenito govoreći.

Zapazimo vezu između (vektorskih i višestruko povezanih Markovljevih procesa: -povezani Markovljev niz također se može tumačiti kao vektor (veličine k) Markovljev niz

5.4.5. Gausov Markovljev proces.

Markovljev proces se naziva Gausovim ako njegova distribucija poštuje normalni zakon raspodjele vjerovatnoće (vidi odjeljak 5.2.1). Kao i za bilo koji Gausov proces, korelaciona funkcija Gausovog Markovljevog procesa daje njegov potpuni probabilistički opis. Može se dokazati da je slučajni proces centrirani Gausov Markovljev proces ako i samo ako na svojoj korelacionoj funkciji zadovoljava jednadžbu

Za homogeni Gausov Markovljev proces, uvjet (5.71) je zapisan korištenjem normalizirane korelacijske funkcije, koja prirodno ovisi o jednom argumentu

Osim trivijalnog rješenja, jednačina (5.72) ima jedinstveno rješenje

Dakle, stacionarni centrirani Gausov proces sa disperzijom je Markovičan ako i samo ako je njegova korelaciona funkcija (slika 5.4)

ili odgovarajuću spektralnu gustinu procesne snage (slika 5.5)

Iz (5.74) i, prema tome, iz (5.75) proizilazi da je homogeni Gausov Markovljev proces kontinuiran u srednjem kvadratu, ali problem 5.6 također nije diferencibilan u srednjem kvadratu.

Rice. 5.4. Normalizovana korelaciona funkcija homogenog Gausovog Markovljevog procesa

Rice. 5.5. Spektralna gustina snage homogenog Gausovog Markovljevog procesa

5.4.6. Gausov Markovljev niz.

Neka je niz centriranih Gausovih slučajnih varijabli sa varijacijama i koeficijentima korelacije. Da bi ovaj niz bio Markovian, potrebno je i dovoljno da

Za stacionarni Gausov Markovljev niz, iz (5.76) slijedi

gdje je koeficijent korelacije između dva susjedna člana niza.

Svaka podsekvenca Gausovog Markovljevog niza je takođe Gausova, Markova.

5.4.7. Diferencijalna jednadžba za gustinu vjerovatnoće prijelaza kontinuiranog Markovljevog procesa.

Rješavanje Kolmogorov-Chapman integralne jednačine (5.62) je težak zadatak. Određivanje gustine vjerovatnoće prijelaza Markovljevog procesa može se svesti na rješavanje diferencijalne jednadžbe ako se ograničimo na kontinuirane procese. Markovljev proces se naziva kontinuiranim ako su vidljivi pokreti mogući samo sa malom vjerovatnoćom u kratkim vremenskim periodima. Tačnije, ovo znači da je svejedno

Realizacije kontinuiranog Markovljevog procesa sa vjerovatnoćom jedan su kontinuirane.

Iz jednačine (5.62), pretpostavljajući i mijenjajući oznake varijabli, dobijamo

Štaviše, očigledno je da

Iz posljednje dvije jednakosti slijedi

Pretpostavimo da se gustina vjerovatnoće prijelaza može proširiti u Taylorov red

Zamjenom (5.80) u (5.79), dijeljenjem obje strane sa i prelaskom na granicu u dobijamo

5.4.8. Difuzijski procesi.

Ako su funkcije konačne osim nule i za , tada se kontinuirani Markovljev proces naziva difuzija. Iz (5.81) slijedi da gustina vjerovatnoće tranzicije procesa difuzije zadovoljava parcijalnu diferencijalnu jednačinu

nazvana inverzna Kolmogorovljeva jednačina.

Slično, može se dokazati da gustina vjerovatnoće tranzicije procesa difuzije zadovoljava direktnu Kolmogorovljevu jednačinu:

koeficijent drifta, i

Koeficijent difuzije.

Direktna Kolmogorovljeva jednačina (5.84) poznata je i kao Foker-Plavka jednačina. Jednačine (5.83) i (5.84) pripadaju klasi paraboličkih parcijalnih diferencijalnih jednačina. U (5.83) varijable su, a varijable y i T uključene su samo u uslov. U (5.84) varijable su y i i t ulaze samo kroz početni uslov. Razmatraju se, na primjer, metode za rješavanje Kolmogorovljevih jednačina.

5.4.9. Stacionarni difuzijski procesi.

Za stacionarne difuzijske procese, koeficijenti pomaka (5.85) i difuzija (5.86) ne ovise o vremenskom parametru, a gustoća vjerovatnoće prijelaza ovisi samo o razlici . Tada iz (5.84) dobijamo

sa početnim stanjem

Ako postoji granica gustoće vjerojatnosti prijelaza koja ne ovisi o početnom stanju, onda se to naziva granična funkcija distribucije stacionarnog difuznog procesa

Iz (5.88) slijedi da . Stoga se granična funkcija raspodjele može naći iz obične diferencijalne jednadžbe prvog reda

čije rješenje ima oblik

konstante se određuju iz uslova normalizacije i graničnog uslova

5.4.10. Gausov proces difuzije.

Razmotrite Gausov stacionarni slučajni proces sa nultom srednjom vrednošću, varijansom i normalizovanom korelacionom funkcijom. Uslovna gustina distribucije ovog slučajnog procesa [vidi (2.74)]

Nađimo za razmatranu uslovnu gustinu vjerovatnoće funkcije definirane prema (5.82):

(5.92)

gdje je vrijednost derivacije kako se približava nuli s desne strane. Ako je kontinuirano na nuli, onda pretpostavimo da trpi diskontinuitet na . Onda

U ovom dijelu koristimo metodu Markovljevog procesa da pronađemo optimalni demodulator. Naša prezentacija je površna, pa bi za detaljnije razmatranje zainteresovani čitaoci trebalo da se obrate dodatnim izvorima (posebno,). I ovaj put ćemo pretpostaviti da je poruka Gausov slučajni proces sa konačnim prikazom u varijablama stanja, tj.

gdje je bijeli Gausov slučajni proces s kovarijansnom funkcijom

Iako ovu činjenicu ne koristimo u našoj raspravi, treba istaći da se postupak opisan u ovom dijelu može izvesti i kada su jednadžba stanja i jednačina opažanja nelinearne i imaju oblik

Imajte na umu da je pod određenim ograničenjima nametnutim vektorski Markovljev proces, koji nije nužno Gausov. Nijedna od prethodno razmatranih metoda ne dozvoljava rješavanje problema s porukama ove klase. Većina rezultata koji će se dobiti u ovom odeljku može se dobiti i za opštiji proces opisan jednačinama (78) i (79).

Vratimo se sada na model u obliku slučajnog procesa opisanog relacijama.Radi jednostavnosti notacije, razmotrićemo poruku koja je skalarni Gausov Markovljev proces i kojom se prenesena oscilacija modulira nekom inercijom -slobodan tip modulacije. Prihvaćena vibracija je zapisana u formi

Proces poruke zadovoljava diferencijalnu jednačinu prvog reda

Dakle, za bilo koje konačne vrijednosti, poruka je stacionarni proces i ima Butterworthov spektar prvog reda. Nadalje, zbog činjenice da je Markovljev proces prvog reda, njegova gustina vjerovatnoće u odsustvu ikakvih opservacija zadovoljava Fokker-Planckovu jednačinu [vidi (3.79)]

Međutim, budući da je posmatrana tokom vremenskog intervala, gustina verovatnoće koja nas zanima nije bezuslovna gustina, već gustina usled uočene oscilacije. Označimo ovu gustinu sa

Imajte na umu da je (86) gustina vjerovatnoće jedne slučajne varijable (vrijednost koja označava vrijednost a u trenutku zbog uočene oscilacije i dobro je definirana karakteristika. Može se pokazati da ova gustina vjerovatnoće zadovoljava jednačina

gdje se matematička očekivanja uzimaju iz gustine.Ako formalno uvedemo izvod

tada se (87) može formalno zapisati kao diferencijalna jednačina

Odnos između posteriorne gustine i procjene minimalne srednje kvadratne greške je dobro poznat. Procjena minimalne srednje kvadratne greške je uslovni prosjek zadnje gustine (vidi str. 73 prvog toma), tj.

Množenjem obe strane (89) sa A, integrišući i uzimajući u obzir odgovarajuće uslove na krajevima intervala, dobijamo (vidi problem 7.2.2)

Imajte na umu da (91) još uvijek sadrži matematičko očekivanje od Kao što bi se očekivalo, ova jednačina se ne može riješiti za opći slučaj modulacije. U slučaju metoda linearne modulacije, lako je pokazati (na primjer, 18] ili problem 7.2.1) da se to svodi na Za mnoge probleme nelinearne modulacije, uspjeh se može postići proširenjem u niz različitih termina jednačina ( 91). Zatim, ako pretpostavimo da je greška procene mala i nametnemo neke uslove na momente viših redova, možemo zanemariti članove drugog i višeg reda i dobiti sledeću približnu jednačinu (detaljno izvođenje dato je u poglavlju 4 knjige ):

gdje označava približnu procjenu na osnovu minimalne srednje kvadratne greške. Funkcija je približna uslovna [prema srednjoj kvadratnoj grešci, koja zadovoljava diferencijalnu jednadžbu

sa graničnim uslovom

Imajte na umu da su jednadžba procjene (92) i jednačina disperzije (93) povezane. Dalje imajte na umu da uslovna srednja kvadratna greška [tj. e. greška, pod uslovom da su aproksimacije koje se moraju izvršiti da bi se dobile prihvaćene validne kada je greška mala.

Vidimo da se jednačina (92) može implementirati u obliku blok dijagrama prikazanog na Sl. 7.3. Ova implementacija je vrlo slična strukturi estimatora maksimalne posteriorne vjerovatnoće sintetizirane u Pogl. 2, sa jedinom razlikom što se sada filter u petlji automatski implementira. Nedostatak ove implementacije je prisutnost komunikacije između petlji.

U slučaju kutne modulacije, može se pokazati da se ova sprega obično može zanemariti. Na primjer, sa faznom modulacijom

Pretpostavlja se da je mnogo veća od najveće frekvencije u spektru poruke i da je sistem u statistički stacionarnom stanju. U ovom slučaju se pokazuje da

zadovoljava disperzijsku jednačinu prilikom zamjene

Za Markovljev proces prvog reda, ova jednačina ima oblik

Blok dijagram prijemnika prikazan je na sl. 7.4. Ova struktura se tačno poklapa sa implementiranim delom aproksimativnog maksimalnog prijemnika posteriorne verovatnoće, koji je ranije sintetizovan (vidi problem u (68)) sada se može tumačiti kao približna uslovna srednja kvadratna greška.

Rice. 7.4. Optimalni prijemnik: fazna modulacija, komunikacija sa Butterworthovim spektrom prvog reda.

Budući da je većina detalja izlaza izostavljena, važno je napomenuti ograničenja rezultata. Diferencijalna jednačina (91) koja određuje uslovni prosjek je tačna. Međutim, aproksimacije povezane sa dobijanjem (92)-(93) odgovaraju linearizujućoj pretpostavci. Stoga je naš rezultat približna procjena zasnovana na minimalnoj srednjoj kvadratnoj grešci koja odgovara prvom članu proširenja serije tačne procjene. Da bi se dobila bolja aproksimacija, može se zadržati veći broj ekspanzijskih termina (vidi, na primjer,). Poteškoća s ovim postupkom je u tome što je dvočlana aproksimacija već toliko složena da vjerovatno nije od praktičnog interesa.

Neka se s.p. pojavi u nekom sistemu. sa diskretnim stanjima
i diskretno vrijeme, tj. tranzicija sistema iz jednog stanja u drugo dešava se samo u određenim vremenskim trenucima
. Ovi trenuci se zovu stepenice proces (obično razlika između susednih momenata posmatranja
jednak konstantnom broju - dužina koraka uzeta kao jedinica vremena);
početak procesa.

Ovaj s.p. može se posmatrati kao niz (lanac) događaja
.

početno stanje sistema, tj. prije 1. koraka;
stanje sistema nakon 1. koraka,
stanje sistema nakon 2. koraka itd.), tj. događaji poput
Gdje.

Poziva se Markovljev slučajni proces sa diskretnim stanjima i diskretnim vremenom Markov lanac(Markovljev lanac).

Zapiši to Markov lanac, u kojem uslovne vjerovatnoće stanja u budućnosti zavise samo od stanja u posljednjoj fazi (i ne zavise od prethodnih) naziva se jednostavan Markov lanac. (A.A. Markov 1856-1922 - ruski matematičar).

Primjer takvog sistema može poslužiti kao tehnički uređaj čija su moguća stanja sljedeća:

dobar posao;

preventivni pregled i održavanje;

radovi na renoviranju;

otpis zbog neupotrebljivosti;

Grafikon statusa rada prikazan je na slici

Rice. 1.11.(A.A. Belov, itd.)

Iz analize grafa je jasno da iz stanja normalnog rada vrha sistem može ući u stanje preventivnog održavanja , a zatim se vratite na . Ili se preseliti iz u stanju popravke , nakon čega se ili vraća na , ili prijeći u stanje otpisa. Država je konačan, budući da je prijelaz iz njega nemoguć. Prijelaz iz nazad u znači kašnjenje u ovom stanju.

U praksi se često susrećemo sa sistemima čija stanja čine lanac u kojem svako stanje (osim ekstremnih I ) povezan je direktnim i povratnim vezama sa dva susjedna,
i ekstremna stanja - sa jednim susjedom (vidi sliku)

Fig.1.12(Belov...)

Primjer takvog sistema je tehnički uređaj koji se sastoji od sličnih jedinica. Svako stanje sistema karakterizira broj neispravnih čvorova u vrijeme verifikacije.

Glavni cilj studije je pronaći vjerovatnoće stanja na bilo koji
m korak. Izračunat ćemo vjerovatnoće stanja diskretnog sistema

Ovdje ćemo razmotriti samo jednostavne Markovljeve lance. Nadalje, ukratko ćemo razmotriti koncepte kontinuiranih Markovljevih procesa.

Sa diskretnim vremenskim promjenama stanja sistema, svaki prijelaz iz jednog stanja u drugo se naziva korak.

Iz definicije Markovljevog lanca proizilazi da je za njega vjerovatnoća tranzicije sistema u stanju
m korak zavisi samo od stanja sistem je bio na prethodnom
korak.

Gdje
bezuslovna verovatnoća da
U prvom koraku sistem će biti u stanju . Za pronalaženje ovih vjerovatnoća potrebno je poznavati početnu distribuciju vjerovatnoće, tj. vjerovatnoće stanja
u određenom trenutku
(početak procesa) i tzv vjerovatnoće tranzicije
Markov lanac uključen
m korak.

Vjerovatnoća tranzicije
naziva se uslovna vjerovatnoća prijelaza sistema on

m korak, u stanju
m korak je mogla , tj.

(43),

gdje prvi indeks označava broj prethodnog stanja, a drugi indeks broj narednog stanja sistema.

Markov lanac se zove homogena, ako je vrijednost
one. uslovne vjerovatnoće
ne zavise od broja testa, inače se naziva heterogen.

Nadalje, razmatrat ćemo samo homogene lance koji se mogu specificirati pomoću vektora - vjerovatnoća stanja u datom trenutku
i matrice ( nazvana prelazna matrica)

(44)
.

Matrični elementi
imaju osnovna svojstva običnih kvadratnih matrica i dodatno sljedeća svojstva:

A)
, b)
za svaki fiksni
, tj. zbir elemenata svakog reda prelazne matrice jednako jedan (kao vjerovatnoća prijelaza događaja iz jednog stanja u bilo koje drugo moguće stanje - formiranje kompletne grupe događaja).

Vjerovatnoća stanja sistema u sljedećem koraku određena je rekurentnom formulom:

Pod određenim uslovima (ergodičnost, homogenost, odsustvo ciklusa) Markov lanac se uspostavlja stacionarni način rada, u kojem vjerovatnoće stanja sistema ne zavise od broja koraka. Takve vjerovatnoće se nazivaju ekstremno(ili konačne) vjerovatnoće Markovljevog lanca:

Postoji tvrdnja.

Teorema 17.1.Za matrice prelaze verovatnoće stepenice
formula je važeća

(45)
,

Dokaz. Prema pravilu množenja dvije kvadratne matrice
reda koji imamo

Gdje

Štaviše, po definiciji prelazne matrice poznato je da
na bilo koji
.

Zbrojimo obje strane jednakosti
na sve
, i zamjenom redoslijeda zbrajanja nakon primjene svojstva a) dvaput, dobivamo to
tranzicijska matrica u dva koraka. Slično, konzistentno rezonujući korak po korak, dobijamo našu izjavu u opštem slučaju.

Primjer 3. Navedena matrica prijelaza

Pronađite matrice vjerovatnoće prijelaza
.

Na osnovu pravila za množenje dvije matrice dobijamo

Vježbajte. Provjerite da li je jednakost tačna

Treba napomenuti da konačni diskretni Markovljev lanac predstavlja daljnju generalizaciju Bernoullijeve sheme, štaviše, za slučaj zavisnih testova; nezavisni testovi su poseban slučaj Markovljevog lanca. Ovdje pod "događaj"

odnosi se na stanje sistema, a "test" se odnosi na promjenu stanja sistema.

ako " testovi„(eksperimenti) su nezavisni, onda pojava određenog događaja u bilo kom eksperimentu ne zavisi od rezultata prethodno izvedenih testova.

Zadaci. a) Date su prijelazne matrice

1.
;

2.
;

3.
.

Pronađite matricu za svaki slučaj
.

Odgovori: a) 1.
;

2.
;

c) Date su prijelazne matrice

;
.

Nađi
.

Odgovori: c) 1.
;2.
;

3.
.

Komentar. Općenito, diskretno Markov lanac
je Markovljev slučajni proces čiji je prostor stanja konačan ili prebrojiv, i skup indeksa
- skup svih nenegativnih cijelih brojeva ili neki njegov podskup (konačan ili prebrojiv). Možemo razgovarati o tome šta je sa ishodom
th testovima.

Često je zgodno identificirati prostor stanja procesa sa skupom nenegativnih cijelih brojeva
i u ovim slučajevima to kažu je u stanju , Ako
.

Vjerovatnoća pogađanja slučajne varijable
u državi (naziva se vjerovatnoća prijelaza u jednom koraku), kao što je gore spomenuto, označava se
, tj.

Ova notacija naglašava da u opštem slučaju verovatnoće tranzicije zavise ne samo od početnog i krajnjeg stanja, već i od trenutka tranzicije.

U slučajevima kada vjerovatnoće prijelaza u jednom koraku ne zavise od vremenske varijable (tj. od vrijednosti , onda kažu da je Markovljev proces imao stacionarne tranzicijske vjerovatnoće. Dakle, u dalje svrhe, napominjemo da postoji jednakost od koje ne zavisi , And označava vjerovatnoću prijelaza u jednom ispitivanju iz stanja u državi .

Obično vjerovatnoće kombinovano u kvadratnu matricu (konačnu ili prebrojivu) u zavisnosti od procesa koji se razmatra:

i naziva se Markovljeva matrica, ili matrica verovatnoće prelaza Markov lanac.

U matrici
i red predstavlja distribuciju vjerovatnoće r.v.
pod uslovom da
. Ako je broj stanja konačan, onda - konačna kvadratna matrica čiji je red (broj redova) jednak broju stanja.

Naravno, vjerovatnoće zadovoljiti sledeća dva uslova:

A)
,

b)
za svaki fiksni

Uslov b) odražava činjenicu da svako ispitivanje uzrokuje neki prijelaz iz jednog stanja u drugo stanje. Radi praktičnosti, obično razgovaramo i o tranzicija iu slučaju kada stanje ostaje nepromijenjeno. Postoji tvrdnja.

Teorema 17.2.Proces je potpuno definisan ako su date vjerovatnoće(46), tj.

i distribuciju vjerovatnoće slučajne varijable .

Dokaz. Pokažimo to za bilo koje konačno kako se izračunavaju vjerovatnoće

budući da se, prema formuli ukupne vjerovatnoće, sve druge vjerovatnoće vezane za slučajne varijable mogu dobiti sumiranjem članova (članova) oblika (47).

Po definiciji uslovne vjerovatnoće imamo

Ali po definiciji Markovljevog procesa dobijamo

Stavljajući jednakost (49) u (48) dobijamo

Nastavljajući ovaj proces uzastopno, dobijamo:

Proces je u potpunosti definiran. Šta je trebalo dokazati.

Markovljevi slučajni procesi su nazvani po istaknutom ruskom matematičaru A.A. Markov (1856-1922), koji je prvi započeo proučavanje vjerovatnoće odnosa slučajnih varijabli i stvorio teoriju koja se može nazvati "dinamikom vjerovatnoće". Nakon toga, temelji ove teorije postali su početna osnova za opću teoriju slučajnih procesa, kao i tako važne primijenjene nauke kao što su teorija difuzijskih procesa, teorija pouzdanosti, teorija čekanja itd. Trenutno se teorija Markovljevih procesa i njene primjene široko koriste u raznim oblastima nauka kao što su mehanika, fizika, hemija itd.

Zbog komparativne jednostavnosti i jasnoće matematičkog aparata, visoke pouzdanosti i tačnosti dobijenih rješenja, Markovljevi procesi su dobili posebnu pažnju stručnjaka uključenih u istraživanje operacija i teoriju optimalnog donošenja odluka.

Uprkos gore pomenutoj jednostavnosti i jasnoći, praktična primena teorije Markovljevih lanaca zahteva poznavanje nekih pojmova i osnovnih principa o kojima treba razgovarati pre predstavljanja primera.

Kao što je naznačeno, Markovljevi slučajni procesi se odnose na posebne slučajeve slučajnih procesa (SP). Zauzvrat, slučajni procesi se zasnivaju na konceptu slučajne funkcije (SF).

Slučajna funkcija je funkcija čija je vrijednost, za bilo koju vrijednost argumenta, slučajna varijabla (RV). Drugim riječima, SF se može nazvati funkcijom koja na svakom testu poprima neki prethodno nepoznati oblik.

Takvi primjeri SF-a su: fluktuacije napona u električnom kolu, brzina automobila na dionici puta sa ograničenjem brzine, hrapavost površine dijela u određenom području itd.

U pravilu se vjeruje da ako je argument SF-a vrijeme, onda se takav proces naziva slučajnim. Postoji još jedna definicija slučajnih procesa, bliža teoriji odlučivanja. U ovom slučaju, slučajni proces se podrazumijeva kao proces slučajne promjene stanja bilo kojeg fizičkog ili tehničkog sistema u odnosu na vrijeme ili neki drugi argument.

Lako je vidjeti da ako odredite stanje i opišete ovisnost, onda će takva ovisnost biti slučajna funkcija.

Slučajni procesi se klasifikuju prema tipovima stanja i argumentu t. U ovom slučaju, slučajni procesi mogu biti sa diskretnim ili kontinuiranim stanjima ili vremenom.

Pored navedenih primjera klasifikacije slučajnih procesa, postoji još jedno važno svojstvo. Ovo svojstvo opisuje probabilističku vezu između stanja slučajnih procesa. Tako, na primjer, ako u slučajnom procesu vjerovatnoća prelaska sistema u svako sljedeće stanje zavisi samo od prethodnog stanja, onda se takav proces naziva proces bez naknadnog efekta.

Zapazimo, prvo, da se slučajni proces sa diskretnim stanjima i vremenom naziva slučajni niz.

Ako slučajni niz ima Markovljevo svojstvo, onda se zove Markovljev lanac.

S druge strane, ako su u slučajnom procesu stanja diskretna, vrijeme je kontinuirano i svojstvo poslijeefekta je očuvano, onda se takav slučajni proces naziva Markovljev proces s kontinuiranim vremenom.

Za Markovljev slučajni proces se kaže da je homogen ako su vjerovatnoće tranzicije konstantne tokom procesa.

Markovljev lanac se smatra datim ako su data dva uslova.

1. Postoji skup vjerovatnoća tranzicije u obliku matrice:

2. Postoji vektor početnih vjerovatnoća

opisuje početno stanje sistema.

Pored matričnog oblika, model Markovljevog lanca može se predstaviti kao usmjereni ponderirani graf (slika 1).

Rice. 1

Skup stanja sistema Markovljevog lanca klasifikuje se na određeni način, uzimajući u obzir dalje ponašanje sistema.

1. Nepovratni set (slika 2).

Fig.2.

U slučaju skupa koji se ne vraća, mogući su bilo kakvi prijelazi unutar ovog skupa. Sistem može napustiti ovaj skup, ali se ne može vratiti na njega.

2. Povratni set (slika 3).

Rice. 3.

U ovom slučaju su mogući bilo kakvi prijelazi unutar skupa. Sistem može ući u ovaj skup, ali ga ne može napustiti.

3. Ergodični set (slika 4).

Rice. 4.

U slučaju ergodičkog skupa, mogući su bilo kakvi prijelazi unutar skupa, ali su prijelazi iz i u skup isključeni.

4. Upijajući set (slika 5)

Rice. 5.

Kada sistem uđe u ovaj skup, proces se završava.

U nekim slučajevima, uprkos nasumičnosti procesa, moguće je u određenoj mjeri kontrolisati zakone raspodjele ili parametre vjerovatnoće tranzicije. Takvi Markovljevi lanci se nazivaju kontrolirani. Očigledno, uz pomoć kontrolisanih Markovljevih lanaca (CMC), proces donošenja odluka postaje posebno efikasan, o čemu će biti reči kasnije.

Glavna karakteristika diskretnog Markovljevog lanca (DMC) je determinizam vremenskih intervala između pojedinih koraka (faza) procesa. Međutim, često se u stvarnim procesima ovo svojstvo ne opaža i intervali se ispostavljaju slučajni s nekim zakonom raspodjele, iako je Markovljevo svojstvo procesa očuvano. Takvi slučajni nizovi se nazivaju polu-Markovljevim.

Osim toga, uzimajući u obzir prisustvo i odsustvo određenih skupova stanja navedenih gore, Markovi lanci mogu biti apsorbirajući ako postoji barem jedno apsorbirajuće stanje, ili ergodični ako vjerovatnoće tranzicije čine ergodični skup. Zauzvrat, ergodični lanci mogu biti regularni ili ciklični. Ciklični lanci se razlikuju od regularnih po tome što se prilikom prijelaza kroz određeni broj koraka (ciklusa) vraća u neko stanje. Obični lanci nemaju ovo svojstvo.