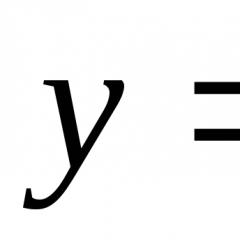Testovi za konvergenciju nepravih integrala. Kako izračunati nepravilan integral i saznati njegovu konvergenciju. Definicija i osnovna svojstva

Teorema 12.11 (test za poređenje nepravih integrala). Neka su funkcije f(x) i g(x) neprekidne na intervalu [a, ">) i na njemu zadovoljavaju uslov 0 fix) ?(x). Zatim iz konvergencije integrala

integral konvergira

i obrnuto, iz divergencije integrala (12.64) slijedi divergencija integrala (12.63).

Dokaz. Hajde da uvedemo sljedeću notaciju:

Funkcija P(K) nije opadajuća; u stvari, ako a ja 2, onda

J popraviti) dx>0, a zatim

Uzmimo niz vrijednosti (/?„) -> “>; zatim odgovarajući niz vrijednosti funkcije (F(Rn)) je monotona i neopadajuća. Neka integral (12.63) konvergira, tada niz (67 ( R to)) je ograničeno; ali tada je i niz ograničen (F(/?„)), što znači da po teoremi 7.13 konvergira. Stoga postoji granica F(R) at R-+ «>, tj. integral (12.64) konvergira.

Dokažimo sada drugi dio teoreme; neka integral (12.64) divergira. Ako pretpostavimo da integral (12.63) konvergira, onda bi, prema onome što je gore dokazano, trebalo da konvergira i integral (12.64), što je u suprotnosti sa uslovom. Teorema je dokazana. ?

Komentar. Sličan kriterij poređenja vrijedi i za nepravilne integrale druge vrste. Ako su funkcije /(x) i g (X) kontinuirano u polu-intervalu [a>b) i za sve tačke u nekoj okolini singularne tačke b završeno

uslovi 0 (x), onda iz konvergencije integrala Jg(x)dx slijedi da

divergenciju integrala J/(x)dx, a od divergencije integrala J/(x)dx -

snaga integrala Jg(x)dx.

Razmotrimo primjere za proučavanje konvergencije nepravilnih integrala.

Primjer 27. T. ^-.

X 3 (1 + e L)

Rješenje. Uporedimo integrand u ovom integralu sa funkcijom

Dg. Očigledno je da -r-

X g* (1+0 x J

gral J-jdx konvergira; dakle, na osnovu kriterijuma poređenja, dato 1 X

nal integral.

Primjer 28. I-.

Rješenje. Uspoređujući integrand ovog integrala sa funkcijom 1/x,

vidimo da je (1 + In x)/x > 1/x na intervalu 1

diverzifikuje, dakle, u poređenju, i ovaj integral divergira.

U zaključku, bez dokaza predstavljamo Cauchyjev kriterij za konvergenciju nepravilnog integrala prve vrste.

12.10.4. Apsolutna i uslovna konvergencija nepravih integrala

Definicija 5. Poziva se nepravilan integral J/(x)dx apsolutno

konvergentan, ako integral J|/(x)|dx konvergira.

Definicija 6. Poziva se nepravilan integral J /(x) dx uslovno slični

trajna, ako konvergira i integral J|/(x)|dx divergira.

Imajte na umu da apsolutna konvergencija integrala implicira njegovu konvergenciju zbog procjene 3 definitivni integral i Cauchyjev kriterijum.

Teorema 12.13 (Dirichlet-Abelov test*). Neka je funkcija /(x) neprekidna i ima ograničeni antiderivativ F(x) na intervalu [a, «>], a funkcija g(x) ima kontinuirani izvod na ovom intervalu, ne raste i teži nuli kao x -> ©o. Zatim nepravilan integral

konvergira.

Dokaz. Primijenimo integraciju po dijelovima na integral J /(x)g(x)dx

na proizvoljnom segmentu R R" sa [ A, °°). Imamo:

Teorema 12.12. Da bi nepravilan integral (12.64) konvergirao, potrebno je i dovoljno da se za bilo koje e > 0 može naći takav broj A> 0, što za bilo koje R" i /?", veće od A, vrijedi nejednakost:

Prema uslovima teoreme F(x) ograničeno, tj. |F(x)| K. Funkcija g(x) ne raste i teži nuli kao x -” “>, što znači. g(x)> 0, a g"(x)

Abel Niels Henrik (1802-1829) - norveški matematičar.

Pošto je, prema uslovima teoreme, g(x) -» 0 za x -> ©°, za proizvoljan broj e > 0 možemo pronaći broj A> takav da kada R" > L nejednakost će biti zadovoljena g(R") Zamjenjujući ovo u procjenu (12.68), dobijamo:

što odgovara Cauchyjevom kriteriju za konvergenciju integrala (12.66). Teorema je dokazana. ?

Razmotrimo primjere korištenja Dirichlet-Abelovog testa za konvergenciju nepravilnih integrala.

Primjer 29. f^^dx, a>0.

Rješenje. Stavimo /(x) = sin x, g(x)= l/x"; lako je provjeriti da su svi uslovi teoreme zadovoljeni, odnosno da ovaj integral konvergira. Za a > 1, ovaj integral

ral apsolutno konvergira. Zaista, |grijeh x/xP 1/d L, integral J(l/x e)dx

konvergira, tj. Po kriterijumu poređenja (teorema 12.11) i ovaj integral apsolutno konvergira.

Primjer 30. Jsin x 2 dx - Fresnel integral, o

Rješenje. Hajde da predstavimo ovaj integral kao zbir:

Pošto je sin x 2 - kontinuirana funkcija na intervalu (0, 1J, postoji prvi integral u (12.69). Da bismo odredili konvergenciju nepravilnog integrala na desnoj strani (12.69), postavljamo /(x) = x sin x 2, g(x) = 1/x. Zatim za funkciju /(x) antiderivat F(x) = -cosx 2 /! je ograničen na interval |1, ">), a #(x) je pozitivan, teži nuli kao x -" °° i ima kontinuirani izvod na (1, ©o). To znači da prema Dirichlet-Abelovom kriteriju drugi integral u (12.69) konvergira, tj. Fresnel integral takođe konvergira.

Kao što znate, pronalaženje integrala može biti prilično težak zadatak. Bilo bi veliko razočaranje početi računati neispravan integral i na kraju puta pronaći da on divergira. Stoga su od interesa metode koje omogućavaju, bez ozbiljnih proračuna zasnovanih na jednoj vrsti funkcije, da se izvede zaključak o konvergenciji ili divergenciji nepravilnog integrala. Prva i druga teorema poređenja, o kojima će biti riječi u nastavku, uvelike pomažu proučavanju nepravilnih integrala za konvergenciju.

Neka je f(x)?0. Zatim funkcije

monotono rastu u varijablama t ili -g (pošto uzimamo g>0, -g teži nuli slijeva). Ako, kako se argumenti povećavaju, funkcije F 1 (t) i F 2 (-d) ostaju ograničene odozgo, to znači da odgovarajući nepravilni integrali konvergiraju. Ovo je osnova prve teoreme poređenja za integrale nenegativnih funkcija.

Neka funkcije f(x) i g(x) na x?a zadovoljavaju sljedeće uvjete:

• 1) 0?f(x)?g(x);
• 2) Funkcije f(x) i g(x) su kontinuirane.

Tada iz konvergencije integrala slijedi konvergencija integrala, a iz divergencije integrala slijedi divergencija

Pošto je 0?f(x)?g(x) i funkcije su neprekidne, onda

Po uslovu, integral konvergira, tj. ima konačnu vrijednost. Dakle, integral takođe konvergira.

Sada neka se integral diverguje. Pretpostavimo da integral konvergira, ali tada integral mora konvergirati, što je u suprotnosti sa uslovom. Naša pretpostavka je netačna, integral divergira.

Teorema poređenja za nepravilne integrale 2. vrste.

Neka se za funkcije f(x) i g(x) na intervalu povećavaju bez ograničenja za x>+0. Za x>+0 vrijedi sljedeća nejednakost:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.

Teorema poređenja za nepravilne integrale 1. vrste.

Neka su funkcije f(x) i g(x) na intervalu , a segment integracije je konačan, odnosno ograničen brojevima, a ne beskonačnošću. Neki zadaci dovode do potrebe da se napuste ova ograničenja. Tako se pojavljuju nepravilni integrali.

Geometrijsko značenje nepravilnog integrala Ispada sasvim jednostavno. U slučaju kada je graf funkcije y = f(x) je iznad ose Ox, određeni integral izražava površinu krivolinijskog trapeza omeđenog krivom y = f(x) , x-osa i ordinate x = a , x = b. Zauzvrat, nepravilan integral izražava površinu neograničenog (beskonačnog) krivolinijskog trapeza zatvorenog između linija y = f(x) (na slici ispod - crvena), x = a i os apscise.

Nepravilni integrali su definisani slično za druge beskonačne intervale:

Površina beskonačnog zakrivljenog trapeza može biti konačan broj, u kom slučaju se nepravilan integral naziva konvergentan. Površina također može biti beskonačna, a u ovom slučaju nepravilni integral se naziva divergentan.

Korištenje granice integrala umjesto samog nepravilnog integrala. Da biste procijenili nepravilan integral, morate koristiti granicu određenog integrala. Ako ova granica postoji i konačna je (nije jednaka beskonačnosti), onda se nepravilni integral naziva konvergentan, a inače - divergentan. Ono čemu varijabla teži pod graničnim predznakom zavisi od toga da li imamo posla s nepravilnim integralom prve ili druge vrste. Hajde da saznamo o ovome sada.

Nepravilni integrali prve vrste - sa beskonačnim granicama i njihovom konvergencijom

Nepravilni integrali sa beskonačnom gornjom granicom

Dakle, pisanje nepravilnog integrala razlikuje se od uobičajenog određenog integrala po tome što je gornja granica integracije beskonačna.

Definicija. Nepravilan integral sa beskonačnom gornjom granicom integracije kontinuirane funkcije f(x) u intervalu od a prije ∞ naziva se granica integrala ove funkcije sa gornjom granicom integracije b i donja granica integracije a pod uslovom da gornja granica integracije raste neograničeno, tj.

.

Ako ova granica postoji i jednaka je nekom broju, a ne beskonačnosti, onda nepravilan integral se naziva konvergentan, a broj kojem je granica jednaka uzima se kao njegova vrijednost. Inače nepravilan integral se naziva divergentan i tome se ne pripisuje nikakvo značenje.

Primjer 1. Izračunajte nepravilan integral(ako se konvergira).

Rješenje. Na osnovu definicije nepravilnog integrala nalazimo

Pošto granica postoji i jednaka je 1, onda je ovo nepravilan integral konvergira i jednako je 1.

U sljedećem primjeru, integrand je skoro isti kao u primjeru 1, samo stepen x nije dva, već slovo alfa, a zadatak je proučavanje neispravnog integrala za konvergenciju. Odnosno, ostaje da se odgovori na pitanje: na kojim vrijednostima alfa ovaj nepravilni integral konvergira, a na kojim vrijednostima se divergira?

Primjer 2. Ispitati nepravilan integral za konvergenciju(donja granica integracije je veća od nule).

Rješenje. Hajde da prvo pretpostavimo da , Onda

U rezultirajućem izrazu prelazimo na granicu na:

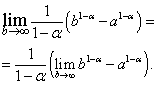
Lako je vidjeti da granica na desnoj strani postoji i jednaka je nuli kada , To jest , I ne postoji kada , To je .

U prvom slučaju, odnosno kada . Ako onda i ne postoji.

Zaključak naše studije je sljedeći: ovo nepravilan integral konvergira at and divergira u .

Primjena Newton-Leibnizove formule na tip nepravilnog integrala koji se proučava , možete izvesti sljedeću formulu, koja je vrlo slična njoj:

.

Ovo je generalizirana Newton-Leibnizova formula.

Primjer 3. Izračunati nepravilan integral(ako se konvergira).

Granica ovog integrala postoji:

Drugi integral, koji čini zbir koji izražava originalni integral:

Granica ovog integrala takođe postoji:

.

Nalazimo zbir dva integrala, koji je ujedno i vrijednost originalnog nepravilnog integrala sa dvije beskonačne granice:

Nepravilni integrali druge vrste - od neograničenih funkcija i njihove konvergencije

Neka funkcija f(x) dato na segmentu od a prije b i na njemu je neograničen. Pretpostavimo da funkcija ide u beskonačnost u tački b , dok je u svim ostalim tačkama segmenta kontinuiran.

Definicija. Nepravilan integral funkcije f(x) na segmentu od a prije b naziva se granica integrala ove funkcije sa gornjom granicom integracije c , ako pri težnji c To b funkcija se povećava bez ograničenja, i to u tački x = b funkcija nije definirana, tj.

.

Ako ova granica postoji, onda se nepravilni integral druge vrste naziva konvergentan, u suprotnom se naziva divergentan.

Koristeći Newton-Leibniz formulu, izvodimo.

1. Nepravilni integrali s beskonačnim granicama

Prisjetimo se definicije integrala kao granice integralnih suma:

Definicija pretpostavlja da je interval integracije konačan i da je funkcija f(x) kontinuirana unutar njega. Kršenje ovih pretpostavki dovodi do nepravilnih integrala.

Definicija. Ako integral teži konačnoj granici kako se neograničeno povećava "b", tada se ova granica naziva nepravilnim integralom s beskonačnom gornjom granicom funkcije f (x) i označava se simbolom

U ovom slučaju, kaže se da nepravilan integral postoji ili konvergira.

Ako navedena granica ne postoji ili postoji, ali je beskonačna, onda se kaže da integral ne postoji ili da divergira.

Nepravilan integral s beskonačnom donjom granicom definira se slično:

Nepravilan integral sa dve beskonačne granice je dat sa:

gdje je c bilo koja fiksna tačka na Ox osi.

Dakle, nepravilni integrali mogu imati beskonačnu donju granicu, beskonačnu gornju granicu, kao i dvije beskonačne granice.

Znakovi konvergencije. Apsolutna i uslovna konvergencija

Integral postoji samo ako postoji svaki od integrala: i .

Primjer. Ispitati konvergenciju integrala

Uz pretpostavku c = 0, dobijamo:

one. integral konvergira.

Ponekad nema potrebe za izračunavanjem nepravilnog integrala, već je dovoljno samo znati da li konvergira ili divergira upoređujući ga s drugim integralom.

Teorema poređenja za nepravilne integrale.

Neka funkcija f (x) u intervalu ima nekoliko (konačan broj) tačaka diskontinuiteta prve vrste, ova „prepreka“ se može lako eliminisati dijeljenjem segmenta na nekoliko segmenata sa tačkama diskontinuiteta, izračunavanjem definitivnih integrala na svakom pojedinačnom presjeku i sabiranje rezultata.

Razmotrimo definitivni integral funkcije koji je neograničen kada se približava jednom od krajeva segmenta, na primjer, .

(U takvim slučajevima obično kažu: „Funkcija ima beskonačan diskontinuitet na desnom kraju intervala integracije.“).

Jasno je da uobičajena definicija integrala ovdje gubi smisao.

Definicija. Nepravilan integral funkcije f(x), kontinuiran za a £ x< b и неограниченной при x ® b - 0, называется предел:

Nepravilan integral funkcije koja ima beskonačan diskontinuitet na lijevom kraju segmenta definira se na sličan način:

Posljedično, u dijelu [-1, 0] integral divergira.

To znači da i integral divergira u presjeku.

Dakle, ovaj integral divergira u cijelom intervalu [-1, 1]. Imajte na umu da ako bismo počeli da računamo ovaj integral ne obraćajući pažnju na diskontinuitet integrala u tački x = 0, dobili bismo netačan rezultat. stvarno,

, što je nemoguće.

Dakle, za proučavanje nepravilnog integrala diskontinuirane funkcije, potrebno ga je „podijeliti“ na nekoliko integrala i proučiti ih.

Ako integrand ima diskontinuitet druge vrste na (konačnom) intervalu integracije, govorimo o nepravilnom integralu druge vrste.

10.2.1 Definicija i osnovna svojstva

Označimo interval integracije sa $\left[ a, \, b \right ]$; pretpostavlja se da su oba ova broja konačna ispod. Ako postoji samo 1 diskontinuitet, on se može nalaziti ili u tački $a$, ili u tački $b$, ili unutar intervala $(a,\,b)$. Razmotrimo prvo slučaj kada postoji diskontinuitet druge vrste u tački $a$, au ostalim tačkama funkcija integranda je kontinuirana. Dakle, raspravljamo o integralu

\begin(jednačina) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(jednačina)

i $f(x) \rightarrow \infty $ kada je $x \rightarrow a+0$. Kao i prije, prvo što treba učiniti je dati značenje ovom izrazu. Da biste to učinili, razmotrite integral

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

Definicija. Neka postoji konačna granica

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

Tada se kaže da nepravilan integral druge vrste (22) konvergira i pripisuje mu se vrijednost $A$; kaže se da je sama funkcija $f(x)$ integrabilna na intervalu $\left[ a, \ , b\right]$.

Razmotrimo opciju kada postoji diskontinuitet druge vrste u funkciji integranda na gornjoj granici intervala integracije. Ovaj slučaj se može svesti na prethodni promjenom varijable $x=-t$ i zatim preuređivanjem granica integracije.

Razmotrimo opciju kada integrand funkcija ima diskontinuitet druge vrste unutar integracionog intervala, u tački $c \in (a,\,b)$. U ovom slučaju, originalni integral

\begin(jednačina) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(jednačina)

predstavljeno kao zbir

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Definicija. Ako se oba integrala $I_1, \, I_2$ konvergiraju, onda se nepravilni integral (23) naziva konvergentnim i dodjeljuje mu se vrijednost jednaka zbroju integrala $I_1, \, I_2$, funkciji $f(x)$ naziva se integrabilnim na intervalu $\left [a, \, b\right]$. Ako je barem jedan od integrala $I_1,\, I_2$ divergentan, nepravilni integral (23) naziva se divergentan.

Konvergentni nepravilni integrali 2. vrste imaju sva standardna svojstva običnih određenih integrala.

1. Ako su $f(x)$, $g(x)$ integrabilni na intervalu $\left[ a, \,b \right ]$, tada je njihov zbir $f(x)+g(x)$ takođe integrabilan na ovom intervalu, i \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Ako je $f(x)$ integrabilno na intervalu $\left[ a, \, b \right ]$, tada je za bilo koju konstantu $C$ funkcija $C\cdot f(x)$ također integrabilan na ovom intervalu, i \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Ako je $f(x)$ integrabilno na intervalu $\left[ a, \, b \right ]$, i na ovom intervalu $f(x)>0$, tada je \[ \int _a^ (b ) f(x)dx\,>\,0. \] 4. Ako je $f(x)$ integrabilno na intervalu $\left[ a, \, b \right ]$, tada su za bilo koje $c\in (a, \,b)$ integrali \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] također konvergiraju, i \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (aditivnost integrala po intervalu).

Razmotrimo integral

\begin(jednačina) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(jednačina)

Ako je $k>0$, integrand teži $\infty$ kao $x \rightarrow +0$, tako da je integral nepravilan druge vrste. Hajde da predstavimo funkciju

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

U ovom slučaju antiderivat je poznat, dakle

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

za $k \neq 1$,

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

za $k = 1$. Uzimajući u obzir ponašanje na $\epsilon \rightarrow +0$, dolazimo do zaključka da integral (20) konvergira na $k

10.2.2 Testovi za konvergenciju nepravilnih integrala 2. vrste

Teorema (prvi znak poređenja). Neka su $f(x)$, $g(x)$ neprekidni za $x\in (a,\,b)$ i $0 1. Ako je integral \[ \int _a^(b)g(x) dx \] konvergira, tada integral \[ \int _a^(b)f(x)dx konvergira. \] 2. Ako se integral \[ \int _a^(b)f(x)dx \] divergira, tada se divergira integral \[ \int _a^(b)g(x)dx. \]

Teorema (drugi kriterij poređenja). Neka su $f(x)$, $g(x)$ kontinuirani i pozitivni za $x\in (a,\,b)$, i neka postoji konačna granica

\[ \theta = \lim_(x \rightarrow a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Zatim integrali

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

konvergiraju ili divergiraju istovremeno.