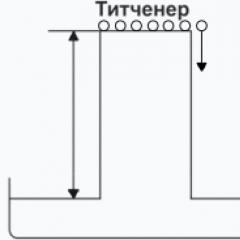
Absolute error of the Simpson method. Trapezoid method. Choice of integration step
This method proposes to approximate the integrand on a partial segment by a parabola passing through the points
(x j , f(x j)), Where j = i-1; i-0.5; i, that is, we approximate the integrand function by a Lagrange interpolation polynomial of the second degree:
After carrying out the integration, we get:
That's what it is Simpson's formula
or the parabolic formula. On the segment
[a, b] Simpson's formula takes the form
A graphical representation of the Simpson method is shown in Fig. 2.4.
Rice. 10.4. Simpson method
Let’s get rid of fractional indices in expression (2.16) by redesignating the variables:
Then Simpson's formula takes the form
The error of formula (2.18) is estimated by the following expression:
Where h·n = b-a, . Thus, the error of Simpson's formula is proportional to O(h 4).
Comment. It should be noted that in Simpson’s formula the integration segment is necessarily divided into even number of intervals.
10.5. Calculation of definite integrals by methods
Monte Carlo
The methods discussed earlier are called deterministic , that is, devoid of the element of chance.
Monte Carlo methods(MMK) are numerical methods for solving mathematical problems using the modeling of random variables. MMCs allow one to successfully solve mathematical problems caused by probabilistic processes. Moreover, when solving problems that are not associated with any probabilities, you can artificially come up with a probabilistic model (and even more than one) that allows you to solve these problems. Consider the calculation of the definite integral
When calculating this integral using the rectangle formula, the interval [ a, b] split into N identical intervals, in the middle of which the values of the integrand were calculated. By calculating the function values at random nodes, you can get a more accurate result:
Here γ i is a random number uniformly distributed over the interval
. The error in calculating the MMC integral is ~ , which is significantly greater than that of previously studied deterministic methods.
In Fig. Figure 2.5 presents a graphical implementation of the Monte Carlo method for calculating a single integral with random nodes (2.21) and (2.22).
(2.23)
Rice. 10.6. Integration by Monte Carlo method (2nd case)
As can be seen in Fig. 2.6, the integral curve lies in the unit square, and if we are able to obtain pairs of random numbers uniformly distributed over the interval, then the resulting values (γ 1, γ 2) can be interpreted as the coordinates of a point in the unit square. Then, if quite a lot of these pairs of numbers are obtained, we can approximately assume that
. Here S is the number of pairs of points falling under the curve, and N– the total number of pairs of numbers.
Example 2.1. Calculate the following integral:
The problem was solved using various methods. The results obtained are summarized in table. 2.1.
Table 2.1
Comment. The choice of a table integral allowed us to compare the error of each method and find out the effect of the number of partitions on the accuracy of the calculations.
11 APPROXIMATE SOLUTION OF NONLINEAR
AND TRANSCENDENT EQUATIONS
To find the definite integral by the trapezoidal method, the area of a curvilinear trapezoid is also divided into n rectangular trapezoids with heights h and bases 1, 2, 3,..у n, where n is the number of the rectangular trapezoid. The integral will be numerically equal to the sum of the areas of rectangular trapezoids (Figure 4).
Rice. 4
n - number of partitions

The error of the trapezoidal formula is estimated by the number

The error of the trapezoid formula decreases faster with growth than the error of the rectangle formula. Therefore, the trapezoidal formula allows for greater accuracy than the rectangle method.
Simpson's formula
If for each pair of segments we construct a polynomial of the second degree, then integrate it on the segment and use the additivity property of the integral, we obtain Simpson’s formula.
In Simpson's method, to calculate a definite integral, the entire integration interval is divided into subintervals of equal length h=(b-a)/n. The number of partition segments is an even number. Then, on each pair of adjacent subintervals, the integrand function f(x) is replaced by a Lagrange polynomial of the second degree (Figure 5).
Rice. 5 The function y=f(x) on the segment is replaced by a 2nd order polynomial

Let's consider the integrand on a segment. Let us replace this integrand with a Lagrange interpolation polynomial of the second degree, coinciding with y= at the points:
Let's integrate on the segment:
Let's introduce a change of variables:
Considering the replacement formulas,

After performing the integration, we obtain Simpson's formula:
The value obtained for the integral coincides with the area of a curvilinear trapezoid bounded by an axis, straight lines, and a parabola passing through points. On a segment, Simpson's formula will look like:
In the parabola formula, the value of the function f(x) at odd points of the partition x 1, x 3, ..., x 2n-1 has a coefficient of 4, at even points x 2, x 4, ..., x 2n-2 - coefficient 2 and at two boundary points x 0 =a, x n =b - coefficient 1.
The geometric meaning of Simpson's formula: the area of a curvilinear trapezoid under the graph of the function f(x) on a segment is approximately replaced by the sum of the areas of the figures lying under the parabolas.
If the function f(x) has a fourth-order continuous derivative, then the absolute value of the error of the Simpson formula is no more than
where M is the largest value on the segment. Since n 4 grows faster than n 2, the error of the Simpson formula decreases with increasing n much faster than the error of the trapezoidal formula.
Let's calculate the integral
This integral is easy to calculate:
Let's take n equal to 10, h=0.1, calculate the values of the integrand at the partition points, as well as half-integer points.
Using the formula of average rectangles, we obtain I straight = 0.785606 (the error is 0.027%), using the trapezoid formula I trap = 0.784981 (the error is about 0.054. When using the method of right and left rectangles, the error is more than 3%.
To compare the accuracy of approximate formulas, let us calculate the integral again
but now according to Simpson's formula with n=4. Let's divide the segment into four equal parts by points x 0 =0, x 1 =1/4, x 2 =1/2, x 3 =3/4, x 4 =1 and calculate approximately the values of the function f(x)=1/( 1+x) at these points: 0 =1.0000, 1 =0.8000, 2 =0.6667, 3 =0.5714, 4 =0.5000.
Using Simpson's formula we get
Let us estimate the error of the obtained result. For the integrand function f(x)=1/(1+x) we have: f (4) (x)=24/(1+x) 5, which means that on the segment . Therefore, we can take M=24, and the error of the result does not exceed 24/(2880 4 4)=0.0004. Comparing the approximate value with the exact one, we conclude that the absolute error of the result obtained using the Simpson formula is less than 0.00011. This is in accordance with the error estimate given above and, in addition, indicates that the Simpson formula is much more accurate than the trapezoidal formula. Therefore, Simpson's formula is used more often for approximate calculation of definite integrals than the trapezoidal formula.
Let us split the integration segment [ A, b] to an even number n equal parts in increments h. On each segment [ X 0, X 2], [X 2, X 4],..., [x i-1, x i+1],..., [ x n-2, x n] integrand function f(X) we replace with an interpolation polynomial of the second degree:
![]()
The coefficients of these quadratic trinomials can be found from the conditions for the equality of the polynomial at the points of the corresponding tabular data. We can take as a Lagrange interpolation polynomial of the second degree passing through the points ![]() :
:
![]()
![]()
The sum of elementary areas and (Fig. 3.3) can be calculated using a definite integral. Taking into account the equalities we get
- ![]()

Rice. 3.3. Illustration for Simpson's method
Having carried out such calculations for each elementary segment, we summarize the resulting expressions:
This expression for S is taken as the value of the definite integral:
 (3.35)
(3.35)
The resulting relationship is called Simpson's formula or parabola formula.
This formula can be obtained in other ways, for example, by using the trapezoidal method twice when partitioning the segment [ A, b] into parts with steps h and 2 h or by combining the formulas of rectangles and trapezoids (see Section 3.2.6).
Sometimes Simpson's formula is written using half-integer indices. In this case, the number of segments of the partition P arbitrary (not necessarily even), and Simpson's formula has the form
 (3.36)
(3.36)
It is easy to see that formula (3.36) coincides with (3.35) if formula (3.35) is applied for the number of segments of the partition 2 n and step h/2.
Example. Calculate the integral using Simpson's method
Function values at n = 10, h = 0.1 are given in table. 3.3. Applying formula (3.35), we find
The result of numerical integration using Simpson's method was found to coincide with the exact value (six significant figures).
One of the possible algorithms for calculating a definite integral using Simpson's method is shown in Fig. 3.4. The boundaries of the integration segment [ A, b],error ε, as well as a formula for calculating the values of the integrand y =f(x) .

Rice. 3.4. Simpson method algorithm
Initially, the segment is divided into two parts with a step h =(b- a)/2. The value of the integral is calculated I 1. Then the number of steps is doubled, the value is calculated I 2 in increments h/2. The condition for the end of the account is taken in the form . If this condition is not met, a new step is divided in half, etc.
Note that shown in Fig. 3.4 the algorithm is not optimal: when calculating each approximation I 2 function values are not used f(x), already found at the previous stage. More economical algorithms will be discussed in Section. 3.2.7.
A problem arises about the numerical calculation of a definite integral, which can be solved using formulas called quadrature formulas.
Let us recall the simplest formulas for numerical integration.
Let's calculate the approximate numerical value. We divide the integration interval [a, b] into n equal parts by dividing points  , called nodes of the quadrature formula. Let the values at the nodes be known
, called nodes of the quadrature formula. Let the values at the nodes be known  :
:


Magnitude 
 called the integration interval or step. Note that in practice - calculations, the number i is chosen small, usually it is no more than 10-20. On a partial interval
called the integration interval or step. Note that in practice - calculations, the number i is chosen small, usually it is no more than 10-20. On a partial interval 
 the integrand is replaced by an interpolation polynomial
the integrand is replaced by an interpolation polynomial


which approximately represents the function f (x) on the interval under consideration.
a) Let us keep only one first term in the interpolation polynomial, then


The resulting quadratic formula
called the rectangle formula.
b) Let us keep the first two terms in the interpolation polynomial, then
 (2)
(2)
Formula (2) is called the trapezoidal formula.
c) Integration interval  we will divide it into an even number of 2n equal parts, and the integration step h will be equal to
we will divide it into an even number of 2n equal parts, and the integration step h will be equal to  . On the interval
. On the interval  of length 2h, we replace the integrand with an interpolation polynomial of the second degree, i.e., we retain the first three terms in the polynomial:
of length 2h, we replace the integrand with an interpolation polynomial of the second degree, i.e., we retain the first three terms in the polynomial:

The resulting quadrature formula is called Simpson's formula
 (3)
(3)
Formulas (1), (2) and (3) have a simple geometric meaning. In the formula of rectangles, the integrand function f(x) on the interval  is replaced by a straight line segment y = yk, parallel to the abscissa axis, and in the trapezoidal formula - by a straight line segment
is replaced by a straight line segment y = yk, parallel to the abscissa axis, and in the trapezoidal formula - by a straight line segment  and the area of the rectangle and the rectilinear trapezoid is calculated respectively, which are then summed up. In Simpson's formula, the function f(x) on the interval
and the area of the rectangle and the rectilinear trapezoid is calculated respectively, which are then summed up. In Simpson's formula, the function f(x) on the interval  length 2h is replaced by a square trinomial - a parabola
length 2h is replaced by a square trinomial - a parabola  The area of a curvilinear parabolic trapezoid is calculated, then the areas are summed.
The area of a curvilinear parabolic trapezoid is calculated, then the areas are summed.
CONCLUSION
At the end of the work, I would like to note a number of features of the application of the methods discussed above. Each method of approximate solution of a definite integral has its own advantages and disadvantages; depending on the task at hand, specific methods should be used.
Variable Replacement Method is one of the main methods for calculating indefinite integrals. Even in cases where we integrate by some other method, we often have to resort to changing variables in intermediate calculations. The success of integration depends to a large extent on whether we are able to select such a successful change of variables that would simplify the given integral.
Essentially speaking, the study of integration methods comes down to finding out what kind of variable replacement needs to be made for this or that type of integrand.
Thus, integration of any rational fraction reduces to integrating a polynomial and several simple fractions.
The integral of any rational function can be expressed through elementary functions in final form, namely:
through logarithms - in cases of simple fractions of type 1;
through rational functions - in the case of simple fractions of type 2
through logarithms and arctangents - in the case of simple fractions of type 3
through rational functions and arctangents - in the case of simple fractions of type 4. The universal trigonometric substitution always rationalizes the integrand, but it often leads to very cumbersome rational fractions, for which, in particular, it is almost impossible to find the roots of the denominator. Therefore, whenever possible, partial substitutions are used, which also rationalize the integrand and lead to less complex fractions.
Newton–Leibniz formula is a general approach to finding definite integrals.
As for the techniques for calculating definite integrals, they are practically no different from all those techniques and methods.
Apply in exactly the same way substitution methods(change of variable), method of integration by parts, the same techniques for finding antiderivatives for trigonometric, irrational and transcendental functions. The only peculiarity is that when using these techniques it is necessary to extend the transformation not only to the integrand function, but also to the limits of integration. When replacing the integration variable, do not forget to change the limits of integration accordingly.
Properly from the theorem, the condition for the continuity of the function is a sufficient condition for the integrability of a function. But this does not mean that the definite integral exists only for continuous functions. The class of integrable functions is much wider. For example, there is a definite integral of functions that have a finite number of discontinuity points.
Calculating a definite integral of a continuous function using the Newton-Leibniz formula comes down to finding the antiderivative, which always exists, but is not always an elementary function or a function for which tables have been compiled that make it possible to obtain the value of the integral. In numerous applications, the integrable function is specified in a table and the Newton-Leibniz formula is not directly applicable.
If you need to get the most accurate result, it is ideal Simpson method.
From what has been studied above, we can draw the following conclusion that the integral is used in sciences such as physics, geometry, mathematics and other sciences. Using the integral, the work of the force is calculated, the coordinates of the center of mass and the path traveled by the material point are found. In geometry it is used to calculate the volume of a body, find the arc length of a curve, etc.
Department of Higher Mathematics
Completed by: Matveev F.I.
Checked by: Burlova L.V.
Ulan-Ude.2002
1.Numerical methods of integration
2. Derivation of Simpson's formula
3.Geometric illustration
4.Selection of integration step
5.Examples
1. Numerical methods of integration
The problem of numerical integration is to calculate the integral
Through a series of values of the integrand.
Numerical integration problems have to be solved for functions specified in tables, functions whose integrals are not taken in elementary functions, etc. Let's consider only functions of one variable.
Instead of the function that needs to be integrated, we integrate the interpolation polynomial. Methods based on replacing the integrand with an interpolation polynomial make it possible to estimate the accuracy of the result using the parameters of the polynomial or to select these parameters based on the given accuracy.
Numerical methods can be conditionally grouped according to the method of approximation of the integrand.
Newton-Cotes methods are based on approximating a function by a degree polynomial. The algorithm of this class differs only in the degree of the polynomial. As a rule, the nodes of the approximating polynomial are equirelated.
Spline integration methods are based on approximating a function by a spline-piecewise polynomial.
The methods of the highest algebraic accuracy (Gaussian method) use specially selected unequal nodes that provide a minimum integration error for a given (selected) number of nodes.
Monte Carlo methods are most often used when calculating multiple integrals; nodes are selected randomly, and the answer is probabilistic.

 total error
total error
![]() truncation error
truncation error
rounding error
Regardless of the chosen method, in the process of numerical integration it is necessary to calculate the approximate value of the integral and estimate the error. The error decreases as the n-number increases
segment partitions. However, this increases the rounding error
by summing the values of integrals calculated on partial segments.
The truncation error depends on the properties of the integrand and the length of the partial segment.
2. Derivation of Simpson's formula
If for each pair of segments we construct a polynomial of the second degree, then integrate it and use the additivity property of the integral, we obtain Simpson’s formula.
Let's consider the integrand on the segment . Let us replace this integrand with a Lagrange interpolation polynomial of the second degree, coinciding with at the points:
Let's integrate:

and is called Simpson's formula.
The value obtained for the integral coincides with the area of a curvilinear trapezoid bounded by the axis, straight lines, and a parabola passing through the points
Let us now estimate the integration error using Simpson's formula. We will assume that there are continuous derivatives on the interval ![]() . Let's make up the difference
. Let's make up the difference

It is already possible to apply the mean value theorem to each of these two integrals, since the function is continuous on and non-negative on the first integration interval and non-positive on the second (that is, it does not change sign on each of these intervals). That's why:

(we used the mean value theorem since - is a continuous function; ).
Differentiating twice and then applying the mean value theorem, we obtain another expression for:
![]() , Where
, Where ![]()
From both estimates for it follows that Simpson's formula is exact for polynomials of degree no higher than three. Let's write Simpson's formula, for example, in the form:
If the integration segment is too large, then it is divided into equal parts (assuming ), and then to each pair of adjacent segments, ![]() ,..., apply the Simpson formula, namely:
,..., apply the Simpson formula, namely:
Let's write Simpson's formula in general form:
Error of Simpson's formula - fourth order method:
![]() , (3)
, (3)
Since the Simpson method allows you to get high accuracy, if not too high. Otherwise, the second-order method may give greater accuracy.
For example, for a function, the trapezoidal shape for for gives the exact result, while using Simpson’s formula we get
3. Geometric illustration
 |
On a segment of length 2h, a parabola is constructed passing through three points, ![]() . The area under the parabola, enclosed between the OX axis and the straight lines, is taken equal to the integral.
. The area under the parabola, enclosed between the OX axis and the straight lines, is taken equal to the integral.
A special feature of the application of Simpson's formula is the fact that the number of partitions of the integration segment is even.
If the number of segments of the partition is odd, then for the first three segments one should apply a formula using a parabola of the third degree passing through the first four points to approximate the integrand.
![]() (4)
(4)
This is Simpson's three-eighths formula.
For an arbitrary segment of integration, formula (4) can be “continued”; in this case, the number of partial segments must be a multiple of three (points).
![]() , m=2,3,... (5)
, m=2,3,... (5)
Whole part
You can obtain the Newton-Cotes formulas of higher orders:
 (6)
(6)
Number of partition segments;
The degree of the polynomial used;
Derivative of the th order at the point ;
Splitting step.
Table 1 shows the coefficients. Each line corresponds to one set of intervals by nodes to construct a polynomial of degree k. To use this scheme for more sets (for example, with k=2 and n=6), you need to “continue” the coefficients and then add them.
Table 1:
The error estimation algorithm for the trapezoidal and Simpson formulas can be written as: (7),
where is a coefficient depending on the integration method and the properties of the integrand;
h - integration step;
p - method order.
Runge's rule is used to calculate the error by calculating the integral twice with steps h and kh.
(8) - a posteriori estimate. Then Iref.= +Ro (9), refined value of the integral.
If the order of the method is unknown, it is necessary to calculate I a third time with step , that is:
![]()
from a system of three equations:

with unknowns I, A and p we get:
From (10) it follows  (11)
(11)
Thus, the double calculation method, used the required number of times, allows one to calculate the integral with a given degree of accuracy. The required number of partitions is selected automatically. In this case, you can use multiple calls to the subroutines of the corresponding integration methods without changing the algorithms of these methods. However, for methods that use equally related nodes, it is possible to modify the algorithms and halve the number of calculations of the integrand by using the integral sums accumulated during previous multiple partitions of the integration interval. Two approximate values of the integral and, calculated using the trapezoidal method with steps and, are related by the relation:
Similarly, for integrals calculated using the formula with steps and , the following relations hold true:
![]() ,
,
![]() (13)
(13)
![]()
4. Choice of integration step
To select the integration step, you can use the expression of the remainder term. Take, for example, the remainder of Simpson's formula:
If ê ê, then ê ê ![]() .
.
Based on the given accuracy e of the integration method, we determine the appropriate step from the last inequality.
![]() ,
, ![]() .
.
However, this method requires evaluation (which is not always possible in practice). Therefore, they use other methods for determining the accuracy estimate, which make it possible to select the desired step h during the calculations.
Let's look at one of these techniques. Let
 ,
,
where is the approximate value of the integral with step . Let's reduce the step by half, dividing the segment into two equal parts and ().
Let us now assume that it does not change too quickly, so that it is almost constant: . Then  And
And  , where
, where ![]() , that is
, that is ![]() .
.
From this we can draw the following conclusion: if ![]() , that is, if , , a is the required accuracy, then the step is suitable for calculating the integral with sufficient accuracy. If, then the calculation is repeated in steps and then compared, etc. This rule is called Runge's rule.
, that is, if , , a is the required accuracy, then the step is suitable for calculating the integral with sufficient accuracy. If, then the calculation is repeated in steps and then compared, etc. This rule is called Runge's rule.
However, when applying Runge's rule, it is necessary to take into account the magnitude of the calculation error: as it decreases, the absolute error of the calculation of the integral increases (the dependence on is inversely proportional) and, if small enough, it may turn out to be greater than the error of the method. If it exceeds , then Runge’s rule cannot be applied for this step and the desired accuracy cannot be achieved. In such cases it is necessary to increase the value.
When deriving Runge's rule, you essentially used the assumption that . If there is only a table of values, then the check for “constancy” can be done directly from the table. Further development of the above algorithms allows us to move to adaptive algorithms, in which, by choosing a different integration step in different parts of the integration segment, depending on the properties, the number of calculations of the integrand is reduced.
Another scheme for refining the integral values is the Eithnen process. The integral is calculated in steps, and . Calculating values. Then  (14).
(14).
The measure of accuracy of the Simpson method is taken to be:
5. Examples
Example 1. Calculate the integral using Simpson's formula if given by a table. Estimate the error.
Table 3.
Solution: Let us calculate by formula (1) for and integral .
According to Runge's rule we get Accept.
Example 2. Calculate integral  .
.
Solution: We have . Hence h==0.1. The calculation results are shown in Table 4.
Table 4.
Calculation of the integral using Simpson's formula
| y0=1.00000; -0.329573ê£ 3. Estimates for the error of the Simpson method: £ 0.0000017 for =0.1, £ 0.0000002 for =0.05. To prevent rounding errors from distorting such an accurate result for Simpson's formula, all calculations were carried out with six decimal places. Final results: |