What is the sum of the angles? Theorem on the sum of the angles of a triangle. Types by angle size

Sum of triangle angles- important, but enough simple theme, which is taught in 7th grade geometry. The topic consists of a theorem, a short proof and several logical consequences. Knowledge of this topic helps in solving geometric problems during subsequent study of the subject.

Theorem - what are the angles of an arbitrary triangle added together?

The theorem states that if you take any triangle, regardless of its type, the sum of all angles will invariably be 180 degrees. This is proven as follows:

for example, take triangle ABC, draw a straight line through point B located at the apex and designate it as “a”, straight line “a” is strictly parallel to side AC;
between straight line “a” and sides AB and BC, angles are designated, marking them with numbers 1 and 2;
angle 1 is considered equal to angle A, and angle 2 is considered equal to angle C, since these angles are considered to lie crosswise;
thus, the sum between angles 1, 2 and 3 (which is designated in place of angle B) is recognized as equal to the unfolded angle with vertex B - and is 180 degrees.

If the sum of the angles indicated by numbers is 180 degrees, then the sum of angles A, B and C is recognized as equal to 180 degrees. This rule is true for any triangle.

What follows from the geometric theorem

It is customary to highlight several corollaries from the above theorem.

If the problem considers a triangle with a right angle, then one of its angles will be equal to 90 degrees by default, and the sum of the acute angles will also be 90 degrees.
If we are talking about a right isosceles triangle, then its acute angles, which add up to 90 degrees, will individually be equal to 45 degrees.
An equilateral triangle consists of three equal angles, respectively, each of them will be equal to 60 degrees, and in total they will be 180 degrees.
The exterior angle of any triangle will be equal to the sum between two interior angles not adjacent to it.

The following rule can be derived: any triangle has at least two acute angles. In some cases, a triangle consists of three acute angles, and if there are only two, then the third angle will be obtuse or right.

Theorem. The sum of the interior angles of a triangle is equal to two right angles.

Let's take some triangle ABC (Fig. 208). Let us denote its interior angles by numbers 1, 2 and 3. Let us prove that

∠1 + ∠2 + ∠3 = 180°.

Let us draw through some vertex of the triangle, for example B, a straight line MN parallel to AC.

At vertex B we got three angles: ∠4, ∠2 and ∠5. Their sum is a straight angle, therefore it is equal to 180°:

∠4 + ∠2 + ∠5 = 180°.

But ∠4 = ∠1 are internal crosswise angles with parallel lines MN and AC and secant AB.

∠5 = ∠3 - these are internal crosswise angles with parallel lines MN and AC and secant BC.

This means that ∠4 and ∠5 can be replaced by their equals ∠1 and ∠3.

Therefore, ∠1 + ∠2 + ∠3 = 180°. The theorem has been proven.

2. Property of the external angle of a triangle.

Theorem. External angle of a triangle equal to the sum two internal angles not adjacent to it.

In fact, in triangle ABC (Fig. 209) ∠1 + ∠2 = 180° - ∠3, but also ∠ВСD, the external angle of this triangle, not adjacent to ∠1 and ∠2, is also equal to 180° - ∠3 .

Thus:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Therefore, ∠1 + ∠2= ∠BCD.

The derived property of the exterior angle of a triangle clarifies the content of the previously proven theorem on the exterior angle of a triangle, which stated only that the exterior angle of a triangle is greater than each interior angle of a triangle not adjacent to it; now it is established that the external angle is equal to the sum of both internal angles not adjacent to it.

3. Property of a right triangle with an angle of 30°.

Theorem. Leg right triangle, lying opposite an angle of 30°, is equal to half the hypotenuse.

Let angle B in the right triangle ACB be equal to 30° (Fig. 210). Then its other acute angle will be equal to 60°.

Let us prove that leg AC is equal to half the hypotenuse AB. Let's extend the leg AC beyond the vertex of the right angle C and set aside a segment CM equal to the segment AC. Let's connect point M to point B. The resulting triangle ВСМ is equal to triangle ACB. We see that each angle of triangle ABM is equal to 60°, therefore this triangle is an equilateral triangle.

Leg AC is equal to half AM, and since AM is equal to AB, leg AC will be equal to half the hypotenuse AB.

The sum of the interior angles of a triangle is 180 0. This is one of the fundamental axioms of Euclid's geometry. This is the geometry that schoolchildren study. Geometry is defined as the science that studies the spatial forms of the real world.

What motivated the ancient Greeks to develop geometry? The need to measure fields, meadows - areas of the earth's surface. At the same time, the ancient Greeks accepted that the surface of the Earth was horizontal and flat. Taking this assumption into account, Euclid’s axioms were created, including the sum of the internal angles of a triangle of 180 0.

An axiom is a proposition that does not require proof. How should this be understood? A wish is expressed that suits the person, and then it is confirmed by illustrations. But everything that has not been proven is fiction, something that does not exist in reality.

Taking the earth's surface horizontal, the ancient Greeks automatically accepted the shape of the Earth as flat, but it is different - spherical. There are no horizontal planes or straight lines in nature at all, because gravity bends space. Straight lines and horizontal planes are found only in the human brain.

Therefore, Euclid's geometry, which explains the spatial forms of the fictional world, is a simulacrum - a copy that has no original.

One of Euclid's axioms states that the sum of the interior angles of a triangle is 180 0. In fact, in real curved space, or on the spherical surface of the Earth, the sum of the internal angles of a triangle is always greater than 180 0.

Let's think like this. Any meridian on the globe intersects with the equator at an angle of 90 0. To get a triangle, you need to move another meridian away from the meridian. The sum of the angles of the triangle between the meridians and the side of the equator will be 180 0. But there will still be an angle at the pole. As a result, the sum of all angles will be more than 180 0.

If the sides intersect at an angle of 90 0 at the pole, then the sum of the internal angles of such a triangle will be 270 0. Two meridians intersecting the equator at right angles in this triangle will be parallel to each other, and at the pole intersecting each other at an angle of 90 0 will become perpendiculars. It turns out that two parallel lines on the same plane not only intersect, but can also be perpendiculars at the pole.

Of course, the sides of such a triangle will not be straight lines, but convex, repeating the spherical shape globe. But this is exactly the real world of space.

The geometry of real space, taking into account its curvature in the middle of the 19th century. developed by the German mathematician B. Riemann (1820-1866). But schoolchildren are not told about this.

So, Euclidean geometry, which takes the form of the Earth as flat with a horizontal surface, which in fact it is not, is a simulacrum. Nootic is Riemannian geometry that takes into account the curvature of space. The sum of the interior angles of the triangle in it is greater than 180 0.

Proof

Let ABC" - arbitrary triangle. Let's lead through the top B line parallel to line A.C. (such a straight line is called the Euclidean straight line). Let's mark a point on it D so that the points A And D lay on opposite sides of a straight line B.C..Angles DBC And ACB equal as internal crosswise lying formed by a secant B.C. with parallel lines A.C. And BD. Therefore, the sum of the angles of a triangle at the vertices B And WITH equal to angle ABD.The sum of all three angles of a triangle is equal to the sum of the angles ABD And BAC. Since these angles are interior one-sided ones for parallel A.C. And BD at secant AB, then their sum is 180°. The theorem has been proven.

Consequences

From the theorem it follows that any triangle has two acute angles. Indeed, using proof by contradiction, let us assume that the triangle has only one acute angle or no acute angles at all. Then this triangle has at least two angles, each of which is at least 90°. The sum of these angles is not less than 180°. But this is impossible, since the sum of all the angles of a triangle is 180°. Q.E.D.

Generalization into simplex theory

Where is the angle between the i and j faces of the simplex.

Notes

On a sphere, the sum of the angles of a triangle always exceeds 180°, the difference is called spherical excess and is proportional to the area of the triangle.
In the Lobachevsky plane, the sum of the angles of a triangle is always less than 180°. The difference is also proportional to the area of the triangle.

The cosine theorem is a generalization of the Pythagorean theorem. The square of a side of a triangle is equal to the sum of the squares of its two other sides without twice the product of these sides by the cosine of the angle between them. For a plane triangle with sides a,b,c and angle α... ... Wikipedia

This term has other meanings, see Triangle (meanings). A triangle (in Euclidean space) is geometric figure, formed by three segments that connect three points that do not lie on the same straight line. Three dots,... ... Wikipedia

Standard notation A triangle is the simplest polygon having 3 vertices (angles) and 3 sides; part of the plane bounded by three points that do not lie on the same line and three segments connecting these points in pairs. Vertices of a triangle ... Wikipedia

Ancient Greek mathematician. Worked in Alexandria in the 3rd century. BC e. The main work “Principia” (15 books), containing the foundations of ancient mathematics, elementary geometry, number theory, general theory relationships and methods for determining areas and volumes,... ... encyclopedic Dictionary

- (died between 275 and 270 BC) ancient Greek mathematician. Information about the time and place of his birth has not reached us, but it is known that Euclid lived in Alexandria and the heyday of his activity occurred during the reign of Ptolemy I in Egypt... ... Big Encyclopedic Dictionary

Geometry similar to Euclidean geometry in that it defines the movement of figures, but differs from Euclidean geometry in that one of its five postulates (the second or fifth) is replaced by its negation. Negation of one of Euclidean postulates... ... Collier's Encyclopedia

Triangle . Acute, obtuse and right triangle.

Legs and hypotenuse. Isosceles and equilateral triangle.

Sum of angles of a triangle.

External angle of a triangle. Signs of equality of triangles.

Remarkable lines and points in a triangle: heights, medians,

bisectors, median e perpendiculars, orthocenter,

center of gravity, center of a circumscribed circle, center of an inscribed circle.

Pythagorean theorem. Aspect ratio in an arbitrary triangle.

Triangle is a polygon with three sides (or three angles). The sides of a triangle are often indicated by small letters that correspond to the capital letters representing the opposite vertices.

If all three angles are acute (Fig. 20), then this acute triangle . If one of the angles is right(C, Fig.21), that is right triangle; sidesa, bforming a right angle are called legs; sidecopposite the right angle is called hypotenuse. If one of obtuse angles (B, Fig. 22), that is obtuse triangle.

Triangle ABC (Fig. 23) - isosceles, If two its sides are equal (a= c); these equal sides are called lateral, the third party is called basis triangle. Triangle ABC (Fig. 24) – equilateral, If All its sides are equal (a = b = c). In general ( a ≠ b ≠ c) we have scalene triangle .

Basic properties of triangles. In any triangle:

1. Opposite the larger side lies the larger angle, and vice versa.

2. Equal angles lie opposite equal sides, and vice versa.

In particular, all angles in equilateral triangle are equal.

3. The sum of the angles of a triangle is 180 º .

From the last two properties it follows that every angle in an equilateral

triangle is 60 º.

4. Continuing one of the sides of the triangle (AC, Fig. 25), we get external

angle BCD . The external angle of a triangle is equal to the sum of the internal angles,

not adjacent to it : BCD = A + B.

5. Any side of a triangle is less than the sum of the other two sides and greater

their differences (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Signs of equality of triangles.

Triangles are congruent if they are respectively equal:

a ) two sides and the angle between them;

b ) two corners and the side adjacent to them;

c) three sides.

Signs of equality of right triangles.

Two rectangular triangles are equal if one of the following conditions is met:

1) their legs are equal;

2) the leg and hypotenuse of one triangle are equal to the leg and hypotenuse of the other;

3) the hypotenuse and acute angle of one triangle are equal to the hypotenuse and acute angle of the other;

4) the leg and the adjacent acute angle of one triangle are equal to the leg and the adjacent acute angle of the other;

5) the leg and the opposite acute angle of one triangle are equal to the leg and the opposite acute angle of the other.

Wonderful lines and points in the triangle.

Height triangle isperpendicular,lowered from any vertex to the opposite side ( or its continuation). This side is calledbase of the triangle . The three altitudes of a triangle always intersectat one point, called orthocenter triangle. Orthocenter of an acute triangle (point O , Fig. 26) is located inside the triangle, andorthocenter of an obtuse triangle (point O , fig.27) – outside; The orthocenter of a right triangle coincides with the vertex of the right angle.

Median - This line segment , connecting any vertex of a triangle to the middle of the opposite side. Three medians of a triangle (AD, BE, CF, fig.28) intersect at one point O , always lying inside the triangle and being his center of gravity. This point divides each median in a ratio of 2:1, counting from the vertex.

Bisector - This bisector segment angle from vertex to point intersections with the opposite side. Three bisectors of a triangle (AD, BE, CF, fig.29) intersect at one point Oh, always lying inside the triangle And being center of the inscribed circle(see section “Inscribedand circumscribed polygons").

The bisector divides the opposite side into parts proportional to the adjacent sides ; for example, in Fig. 29 AE: CE = AB: BC.

Median perpendicular is a perpendicular drawn from the middle segment points (sides). Three perpendicular bisectors of triangle ABC(KO, MO, NO, Fig. 30 ) intersect at one point O, which is center circumscribed circle (points K, M, N – the midpoints of the sides of the triangle ABC).

In an acute triangle, this point lies inside the triangle; in obtuse - outside; in a rectangular - in the middle of the hypotenuse. Orthocenter, center of gravity, circumcenter and inscribed circle coincide only in an equilateral triangle.

Pythagorean theorem. In a right triangle, the square of lengthThe hypotenuse is equal to the sum of the squares of the lengths of the legs.

The proof of the Pythagorean theorem follows clearly from Fig. 31. Consider a right triangle ABC with legs a, b and hypotenuse c.

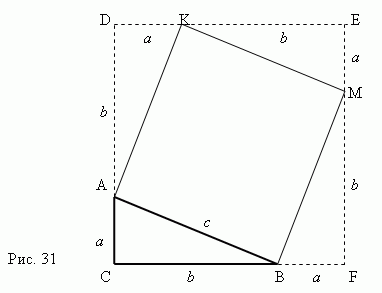
Let's build a square AKMB using the hypotenuse AB as a side. Thencontinue the sides of the right triangle ABC so as to get a square CDEF , whose side is equala + b .Now it is clear that the area of the square CDEF is equal to ( a+b) 2 . On the other hand, this area equals the sum areas four right triangles and the square AKMB, that is

c 2 + 4 (ab / 2) = c 2 + 2 ab,

from here,

c 2 + 2 ab= (a+b) 2 ,

and finally we have:

c 2 =a 2 +b 2 .

Aspect ratio in an arbitrary triangle.

In the general case (for an arbitrary triangle) we have:

c 2 =a 2 +b 2 – 2ab· cos C,

where C – angle between sidesa And b .