What is the modulus and argument of a complex number. Trigonometric notation. Modulus and argument of a complex number. Trigonometric
A complex number is a number of the form z =x + i * y, where x and y are real numbers, and i = imaginary unit (i.e. a number whose square is -1). To define the representation argument comprehensive numbers, you need to look at a complex number on the complex plane in the polar coordinate system.
Instructions
1. The plane on which complex complexes are represented numbers, is called complex. On this plane, the horizontal axis is occupied by real numbers(x), and the vertical axis is imaginary numbers(y). On such a plane, the number is given by two coordinates z = (x, y). In the polar coordinate system, the coordinates of a point are the modulus and the argument. The modulus is the distance |z| from a point to the origin. Is an angle called an argument? between the vector connecting the point and the coordinate preface and the horizontal axis of the coordinate system (see figure).
2. The figure shows that the complex module numbers z = x + i * y is found using the Pythagorean theorem: |z| = ? (x^2 + y^2). Further argument numbers z is found as an acute angle of a triangle - through the values of the trigonometric functions sin, cos, tan:sin? =y/? (x^2 + y^2),cos ? = x / ? (x^2 + y^2),tg ? = y/x.
3. Let's say, let the number z = 5 * (1 + ?3 * i) be given. First of all, select the real and imaginary parts: z = 5 +5 * ?3 * i. It turns out that the real part is x = 5, and the imaginary part is y = 5 * ?3. Calculate modulus numbers: |z| = ?(25 + 75) = ?100 =10. Next, find the sine of the angle?: sin ? = 5 / 10 = 1 / 2. From there we get the argument numbers z is equal to 30°.
4. Example 2. Let the number z = 5 * i be given. From the picture you can see that the angle? = 90°. Check this value using the formula given above. Write down the coordinates of this numbers on the complex plane: z = (0, 5). Module numbers|z| = 5. Tangent of the angle tg? = 5 / 5 = 1. From there it follows what? = 90°.
5. Example 3. Let's say we need to find the argument for the sum of 2 complex numbers z1 = 2 + 3 * i, z2 = 1 + 6 * i. According to the rules of addition, you add these two complex numbers: z = z1 + z2 = (2 + 1) + (3 + 6) * i = 3 + 9 * i. Then, according to the above diagram, calculate the argument: tg? = 9 / 3 = 3.
Note!
If the number z = 0, then the value of the argument for it is not defined.
Helpful advice
The value of the argument of a complex number is determined with an accuracy of 2 * ? * k, where k is any integer. The meaning of the argument? such that –?
Complex numbers
Imaginary And complex numbers. Abscissa and ordinate
complex number. Conjugate complex numbers.
Operations with complex numbers. Geometric
representation of complex numbers. Complex plane.
Modulus and argument of a complex number. Trigonometric
complex number form. Operations with complex
numbers in trigonometric form. Moivre's formula.
Basic information about imaginary And complex numbers are given in the section “Imaginary and complex numbers”. The need for these numbers of a new type arose when solving quadratic equations for the case
D< 0 (здесь D– discriminant of a quadratic equation). For a long time, these numbers did not find physical application, which is why they were called “imaginary” numbers. However, now they are very widely used in various fields of physics.and technology: electrical engineering, hydro- and aerodynamics, elasticity theory, etc.
Complex numbers are written in the form:a+bi. Here a And b – real numbers , A i – imaginary unit, i.e. e. i 2 = –1. Number a called abscissa, a b – ordinatecomplex numbera + bi.Two complex numbersa+bi And a–bi are called conjugate complex numbers.
Main agreements:
1. Real number
Acan also be written in the formcomplex number:a+ 0 i or a – 0 i. For example, records 5 + 0i and 5 – 0 imean the same number 5 .2. Complex number 0 + bicalled purely imaginary number. Recordbimeans the same as 0 + bi.
3. Two complex numbersa+bi Andc + diare considered equal ifa = c And b = d. Otherwise complex numbers are not equal.
Addition. Sum of complex numbersa+bi And c + diis called a complex number (a+c ) + (b+d ) i.Thus, when adding complex numbers, their abscissas and ordinates are added separately.
This definition corresponds to the rules for operations with ordinary polynomials.
Subtraction. The difference of two complex numbersa+bi(diminished) and c + di(subtrahend) is called a complex number (a–c ) + (b–d ) i.
Thus, When subtracting two complex numbers, their abscissas and ordinates are subtracted separately.
Multiplication. Product of complex numbersa+bi And c + di is called a complex number:
(ac–bd ) + (ad+bc ) i.This definition follows from two requirements:
1) numbers a+bi And c + dimust be multiplied like algebraic binomials,
2) number ihas the main property:i 2 = – 1.
EXAMPLE ( a+ bi )(a–bi) =a 2 +b 2 . Hence, work
two conjugate complex numbers is equal to the real
a positive number.
Division. Divide a complex numbera+bi (divisible) by anotherc + di(divider) - means to find the third numbere + f i(chat), which when multiplied by a divisorc + di, results in the dividenda + bi.
If the divisor is not zero, division is always possible.
EXAMPLE Find (8 +i ) : (2 – 3 i) .
Solution. Let's rewrite this ratio as a fraction:
Multiplying its numerator and denominator by 2 + 3i
AND Having performed all the transformations, we get:
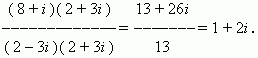
Geometric representation of complex numbers. Real numbers are represented by points on the number line:
Here is the point Ameans the number –3, dotB– number 2, and O- zero. In contrast, complex numbers are represented by points on the coordinate plane. For this purpose, we choose rectangular (Cartesian) coordinates with the same scales on both axes. Then the complex numbera+bi will be represented by a dot P with abscissa a and ordinate b (see picture). This coordinate system is called complex plane .

Module complex number is the length of the vectorOP, representing a complex number on the coordinate ( comprehensive) plane. Modulus of a complex numbera+bi denoted | a+bi| or letter r
Definition 8.3 (1).
Length |z| vector z = (x,y) is called the modulus of the complex number z = x + yi
Since the length of each side of the triangle does not exceed the sum of the lengths of its two other sides, and the absolute value of the difference in the lengths of the two sides of the triangle is not less than the length of the third side, then for any two complex numbers z 1 and z 2 the inequalities hold

Definition 8.3 (2).
Complex number argument. If φ is the angle formed by a non-zero vector z with the real axis, then any angle of the form (φ + 2πn, where n is an integer, and only an angle of this kind, will also be an angle formed by the vector z with the real axis.
The set of all angles formed by the non-zero vector z = = (x, y) with the real axis is called the argument of the complex number z = x + yi and is denoted by arg z. Each element of this set is called the value of the argument of the number z (Fig. 8.3(1)).
Rice. 8.3(1).
Since a non-zero vector of a plane is uniquely determined by its length and the angle it forms with the x axis, then two complex numbers different from zero are equal if and only if their absolute values and arguments are equal.
If, for example, the condition 0≤φ is imposed on the values of the argument φ of the number z<2π или условие -π<φ≤π, то значение аргумента будет определено однозначно. Такое значение называется главным значением аргумента.
Definition 8.3.(3)
Trigonometric form of writing a complex number. The real and imaginary parts of a complex number z = x + уi ≠ 0 are expressed through its modulus r= |z| and the argument φ as follows (from the definition of sine and cosine):
The right side of this equality is called the trigonometric form of writing the complex number z. We will also use it for z = 0; in this case, r = 0, and φ can take any value - the argument of the number 0 is undefined. So, every complex number can be written in trigonometric form.
It is also clear that if the complex number z is written in the form
then the number r is its modulus, since
And φ is one of the values of its argument
The trigonometric form of writing complex numbers can be convenient to use when multiplying complex numbers; in particular, it allows you to find out the geometric meaning of the product of complex numbers.
Let's find formulas for multiplying and dividing complex numbers in trigonometric form. If
then according to the rule of multiplication of complex numbers (using the formulas for sine and cosine of the sum)
Thus, when multiplying complex numbers, their absolute values are multiplied, and the arguments are added:
Applying this formula sequentially to n complex numbers, we get
If all n numbers are equal, we get
Where for
performed
![]()
Hence, for a complex number whose absolute value is 1 (hence, it has the form
![]()
This equality is called Moivre's formulas
In other words, when dividing complex numbers, their modules are divided,
and the arguments are subtracted.
Examples 8.3 (1).
Draw on the complex plane C a set of points satisfying the following conditions:

Which represents a given complex number $z=a+bi$ is called the modulus of the given complex number.
The modulus of a given complex number is calculated using the following formula:
Example 1
Calculate the modulus of the given complex numbers $z_(1) =13,\, \, z_(2) =4i,\, \, \, z_(3) =4+3i$.
We calculate the modulus of a complex number $z=a+bi$ using the formula: $r=\sqrt(a^(2) +b^(2) ) $.
For the original complex number $z_(1) =13$ we obtain $r_(1) =|z_(1) |=|13+0i|=\sqrt(13^(2) +0^(2) ) =\sqrt (169) =13$
For the original complex number $\, z_(2) =4i$ we obtain $r_(2) =|z_(2) |=|0+4i|=\sqrt(0^(2) +4^(2) ) = \sqrt(16) =4$
For the original complex number $\, z_(3) =4+3i$ we get $r_(3) =|z_(3) |=|4+3i|=\sqrt(4^(2) +3^(2) ) =\sqrt(16+9) =\sqrt(25) =5$
Definition 2
The angle $\varphi $ formed by the positive direction of the real axis and the radius vector $\overrightarrow(OM) $, which corresponds to a given complex number $z=a+bi$, is called the argument of this number and is denoted by $\arg z$.
Note 1
The modulus and argument of a given complex number are used explicitly when representing a complex number in trigonometric or exponential form:
- $z=r\cdot (\cos \varphi +i\sin \varphi)$ - trigonometric form;
- $z=r\cdot e^(i\varphi ) $ - exponential form.
Example 2
Write a complex number in trigonometric and exponential forms, given by the following data: 1) $r=3;\varphi =\pi $; 2) $r=13;\varphi =\frac(3\pi )(4) $.
1) Substitute the data $r=3;\varphi =\pi $ into the corresponding formulas and get:
$z=3\cdot (\cos \pi +i\sin \pi)$ - trigonometric form
$z=3\cdot e^(i\pi ) $ - exponential form.
2) Substitute the data $r=13;\varphi =\frac(3\pi )(4) $ into the corresponding formulas and get:
$z=13\cdot (\cos \frac(3\pi )(4) +i\sin \frac(3\pi )(4))$ - trigonometric form
$z=13\cdot e^(i\frac(3\pi )(4) ) $ - exponential form.
Example 3
Determine the modulus and argument of the given complex numbers:
1) $z=\sqrt(2) \cdot (\cos 2\pi +i\sin 2\pi)$; 2) $z=\frac(5)(3) \cdot (\cos \frac(2\pi )(3) +i\sin \frac(2\pi )(3))$; 3) $z=\sqrt(13) \cdot e^(i\frac(3\pi )(4) ) $; 4) $z=13\cdot e^(i\pi ) $.
We will find the modulus and argument using formulas for writing a given complex number in trigonometric and exponential forms, respectively
\ \
1) For the original complex number $z=\sqrt(2) \cdot (\cos 2\pi +i\sin 2\pi)$ we obtain $r=\sqrt(2) ;\varphi =2\pi $.
2) For the initial complex number $z=\frac(5)(3) \cdot (\cos \frac(2\pi )(3) +i\sin \frac(2\pi )(3))$ we obtain $ r=\frac(5)(3) ;\varphi =\frac(2\pi )(3) $.
3) For the initial complex number $z=\sqrt(13) \cdot e^(i\frac(3\pi )(4) ) $ we obtain $r=\sqrt(13) ;\varphi =\frac(3\ pi )(4) $.
4) For the original complex number $z=13\cdot e^(i\pi ) $ we obtain $r=13;\varphi =\pi $.
The argument $\varphi $ of a given complex number $z=a+bi$ can be calculated using the following formulas:
\[\varphi =tg\frac(b)(a) ;\cos \varphi =\frac(a)(\sqrt(a^(2) +b^(2) ) ) ;\sin \varphi =\frac (b)(\sqrt(a^(2) +b^(2) ) .\]
In practice, to calculate the value of the argument of a given complex number $z=a+bi$, the formula is usually used:
$\varphi =\arg z=\left\(\begin(array)(c) (arctg\frac(b)(a) ,a\ge 0) \\ (arctg\frac(b)(a) +\ pi ,a
or solve a system of equations
$\left\(\begin(array)(c) (\cos \varphi =\frac(a)(\sqrt(a^(2) +b^(2) ) ) ) \\ (\sin \varphi = \frac(b)(\sqrt(a^(2) +b^(2) ) ) \end(array)\right. $. (**)
Example 4
Calculate the argument of the given complex numbers: 1) $z=3$; 2) $z=4i$; 3) $z=1+i$; 4) $z=-5$; 5) $z=-2i$.
Since $z=3$, then $a=3,b=0$. Let's calculate the argument of the original complex number using the formula (*):
\[\varphi =\arg z=arctg\frac(0)(3) =arctg0=0.\]
Since $z=4i$, then $a=0,b=4$. Let's calculate the argument of the original complex number using the formula (*):
\[\varphi =\arg z=arctg\frac(4)(0) =arctg(\infty)=\frac(\pi )(2).\]
Since $z=1+i$, then $a=1,b=1$. Let's calculate the argument of the original complex number by solving system (**):
\[\left\(\begin(array)(c) (\cos \varphi =\frac(1)(\sqrt(1^(2) +1^(2) ) ) =\frac(1)(\ sqrt(2) ) =\frac(\sqrt(2) )(2) ) \\ (\sin \varphi =\frac(1)(\sqrt(1^(2) +1^(2) ) ) = \frac(1)(\sqrt(2) ) =\frac(\sqrt(2) )(2) ) \end(array)\right. .\]
From the trigonometry course it is known that $\cos \varphi =\sin \varphi =\frac(\sqrt(2) )(2) $ for the angle corresponding to the first coordinate quarter and equal to $\varphi =\frac(\pi )( 4) $.
Since $z=-5$, then $a=-5,b=0$. Let's calculate the argument of the original complex number using the formula (*):
\[\varphi =\arg z=arctg\frac(0)(-5) +\pi =arctg0+\pi =0+\pi =\pi .\]
Since $z=-2i$, then $a=0,b=-2$. Let's calculate the argument of the original complex number using the formula (*):
\[\varphi =\arg z=arctg\frac(-2)(0) =arctg(-\infty)=\frac(3\pi )(2) .\]
Note 2
The number $z_(3)$ is represented by the point $(0;1)$, therefore, the length of the corresponding radius vector is equal to 1, i.e. $r=1$, and the argument $\varphi =\frac(\pi )(2) $ according to Note 3.
The number $z_(4)$ is represented by the point $(0;-1)$, therefore, the length of the corresponding radius vector is 1, i.e. $r=1$, and the argument $\varphi =\frac(3\pi )(2) $ according to Note 3.
The number $z_(5) $ is represented by the point $(2;2)$, therefore, the length of the corresponding radius vector is equal to $\sqrt(2^(2) +2^(2) ) =\sqrt(4+4) = \sqrt(8) =2\sqrt(2) $, i.e. $r=2\sqrt(2) $, and the argument $\varphi =\frac(\pi )(4) $ by the property of a right triangle.
A complex number is a number of the form z =x + i * y, where x and y are real numbers, and i = imaginary unit (i.e. a number whose square is -1). To define the concept argument comprehensive numbers, it is necessary to consider a complex number on the complex plane in the polar coordinate system.
Instructions
The plane on which complex complexes are represented numbers, is called complex. On this plane, the horizontal axis is occupied by real numbers(x), and the vertical axis is imaginary numbers(y). On such a plane, the number is given by two coordinates z = (x, y). In the polar coordinate system, the coordinates of a point are the modulus and the argument. The modulus is the distance |z| from a point to the origin. The argument is the angle between the vector connecting the point and the origin and the horizontal axis of the coordinate system (see figure).
The figure shows that the complex module numbers z = x + i * y is found using the Pythagorean theorem: |z| = ? (x^2 + y^2). Next argument numbers z is found as an acute angle of a triangle - through the values of the trigonometric functions sin, cos, tg:sin = y / ? (x^2 + y^2),
cos = x / ? (x^2 + y^2),
tg = y/x.
For example, let the number z = 5 * (1 + ?3 * i) be given. First of all, select the real and imaginary parts: z = 5 +5 * ?3 * i. It turns out that the real part is x = 5, and the imaginary part is y = 5 * ?3. Calculate modulus numbers: |z| = ?(25 + 75) = ?100 =10. Next, find the sine of the angle: sin = 5 / 10 = 1 / 2. This gives the argument numbers z is equal to 30°.
Example 2. Let the number z = 5 * i be given. The figure shows that the angle = 90°. Check this value using the formula given above. Write down the coordinates of this numbers on the complex plane: z = (0, 5). Module numbers|z| = 5. Tangent of the angle tg = 5 / 5 = 1. It follows that = 90°.
Example 3. Let it be necessary to find the argument of the sum of two complex numbers z1 = 2 + 3 * i, z2 = 1 + 6 * i. According to the rules of addition, you add these two complex numbers: z = z1 + z2 = (2 + 1) + (3 + 6) * i = 3 + 9 * i. Next, using the above diagram, calculate the argument: tg = 9 / 3 = 3.