How to determine the sign of the projection onto an axis. Basic formulas for finding distances using the projection of a vector onto an axis. Vector product of coordinate unit vectors

§ 3. Projections of a vector on the coordinate axes

1. Finding projections geometrically.

Vector
- projection of the vector onto the axis OX
- projection of the vector onto the axis OY

Definition 1. Vector projection on any coordinate axis is a number taken with a plus or minus sign, corresponding to the length of the segment located between the bases of the perpendiculars dropped from the beginning and end of the vector to the coordinate axis.

The projection sign is defined as follows. If, when moving along the coordinate axis, there is a movement from the projection point of the beginning of the vector to the projection point of the end of the vector in the positive direction of the axis, then the projection of the vector is considered positive. If it is opposite to the axis, then the projection is considered negative.

The figure shows that if the vector is oriented somehow opposite to the coordinate axis, then its projection onto this axis is negative. If a vector is oriented somehow in the positive direction of the coordinate axis, then its projection onto this axis is positive.

If a vector is perpendicular to the coordinate axis, then its projection onto this axis is zero.
If a vector is codirectional with an axis, then its projection onto this axis is equal to the absolute value of the vector.
If a vector is directed oppositely to the coordinate axis, then its projection onto this axis is equal in absolute value to the absolute value of the vector taken with a minus sign.

2. Most general definition projections.

From a right triangle ABD: .

Definition 2. Vector projection on any coordinate axis is a number equal to the product of the modulus of the vector and the cosine of the angle formed by the vector with the positive direction of the coordinate axis.

The sign of the projection is determined by the sign of the cosine of the angle formed by the vector with the positive axis direction.
If the angle is acute, then the cosine has a positive sign and the projections are positive. For obtuse angles, the cosine has a negative sign, so in such cases the projections onto the axis are negative.
- therefore, for vectors perpendicular to the axis, the projection is zero.

In physics for grade 9 (I.K.Kikoin, A.K.Kikoin, 1999),
task №5
to the chapter " CHAPTER 1. GENERAL INFORMATION ABOUT TRAFFIC».

1. What is called the projection of a vector onto the coordinate axis?

1. The projection of vector a onto the coordinate axis is the length of the segment between the projections of the beginning and end of vector a (perpendiculars dropped from these points onto the axis) onto this coordinate axis.

2. How is the displacement vector of a body related to its coordinates?

2. The projections of the displacement vector s on the coordinate axes are equal to the change in the corresponding body coordinates.

3. If the coordinate of a point increases over time, then what sign does the projection of the displacement vector onto the coordinate axis have? What if it decreases?

3. If the coordinate of a point increases over time, then the projection of the displacement vector onto the coordinate axis will be positive, because in this case we will go from the projection of the beginning to the projection of the end of the vector in the direction of the axis itself.

If the coordinate of a point decreases over time, then the projection of the displacement vector onto the coordinate axis will be negative, because in this case we will go from the projection of the beginning to the projection of the end of the vector against the guide of the axis itself.

4. If the displacement vector is parallel to the X axis, then what is the modulus of the projection of the vector onto this axis? And what about the modulus of the projection of the same vector onto the Y axis?

4. If the displacement vector is parallel to the X axis, then the modulus of the vector’s projection onto this axis is equal to the modulus of the vector itself, and its projection onto the Y axis is zero.

5. Determine the signs of the projections onto the X axis of the displacement vectors shown in Figure 22. How do the coordinates of the body change during these displacements?

5. In all the following cases, the Y coordinate of the body does not change, and the X coordinate of the body will change as follows:

a) s 1;

the projection of the vector s 1 onto the X axis is negative and is equal in absolute value to the length of the vector s 1 . With such a movement, the X coordinate of the body will decrease by the length of the vector s 1.

b) s 2 ;

the projection of the vector s 2 onto the X axis is positive and equal in magnitude to the length of the vector s 1 . With such a movement, the X coordinate of the body will increase by the length of the vector s 2.

c) s 3 ;

the projection of the vector s 3 onto the X axis is negative and equal in magnitude to the length of the vector s 3 . With such a movement, the X coordinate of the body will decrease by the length of the vector s 3.

d)s 4;

the projection of the vector s 4 onto the X axis is positive and equal in magnitude to the length of the vector s 4 . With such a movement, the X coordinate of the body will increase by the length of the vector s 4.

e) s 5;

the projection of the vector s 5 on the X axis is negative and equal in magnitude to the length of the vector s 5 . With such a movement, the X coordinate of the body will decrease by the length of the vector s 5.

6. If the value of the distance traveled is large, then can the displacement module be small?

6. Maybe. This is due to the fact that displacement (displacement vector) is a vector quantity, i.e. is a directed straight line segment connecting the initial position of the body with its subsequent positions. And the final position of the body (regardless of the distance traveled) can be as close as desired to the initial position of the body. If the final and initial positions of the body coincide, the displacement module will be equal to zero.

7. Why is the vector of movement of a body more important in mechanics than the path it has traveled?

7. The main task of mechanics is to determine the position of the body at any time. Knowing the vector of movement of the body, we can determine the coordinates of the body, i.e. the position of the body at any moment in time, and knowing only the distance traveled, we cannot determine the coordinates of the body, because we have no information about the direction of movement, but can only judge the length of the path traveled at a given time.

The axis is the direction. This means that projection onto an axis or onto a directed line is considered the same. Projection can be algebraic or geometric. In geometric terms, the projection of a vector onto an axis is understood as a vector, and in algebraic terms, it is understood as a number. That is, the concepts of projection of a vector onto an axis and numerical projection of a vector onto an axis are used.

If we have an L axis and a non-zero vector A B →, then we can construct a vector A 1 B 1 ⇀, denoting the projections of its points A 1 and B 1.

A 1 B → 1 will be the projection of the vector A B → onto L.

Definition 1

Projection of the vector onto the axis is a vector whose beginning and end are projections of the beginning and end of a given vector. n p L A B → → it is customary to denote the projection A B → onto L. To construct a projection onto L, perpendiculars are dropped onto L.

Example 1

An example of a vector projection onto an axis.

On coordinate plane About x y the point M 1 (x 1 , y 1) is specified. It is necessary to construct projections on O x and O y to image the radius vector of point M 1. We get the coordinates of the vectors (x 1, 0) and (0, y 1).

If we are talking about the projection of a → onto a non-zero b → or the projection of a → onto the direction b → , then we mean the projection of a → onto the axis with which the direction b → coincides. The projection of a → onto the line defined by b → is designated n p b → a → → . It is known that when the angle between a → and b → , n p b → a → → and b → can be considered codirectional. In the case where the angle is obtuse, n p b → a → → and b → are in opposite directions. In a situation of perpendicularity a → and b →, and a → is zero, the projection of a → in the direction b → is the zero vector.

The numerical characteristic of the projection of a vector onto an axis is the numerical projection of a vector onto a given axis.

Definition 2

Numerical projection of the vector onto the axis is a number that is equal to the product of the length of a given vector and the cosine of the angle between the given vector and the vector that determines the direction of the axis.

The numerical projection of A B → onto L is denoted n p L A B → , and a → onto b → - n p b → a → .

Based on the formula, we obtain n p b → a → = a → · cos a → , b → ^ , from where a → is the length of the vector a → , a ⇀ , b → ^ is the angle between the vectors a → and b → .

We obtain the formula for calculating the numerical projection: n p b → a → = a → · cos a → , b → ^ . It is applicable for known lengths a → and b → and the angle between them. The formula is applicable for known coordinates a → and b →, but there is a simplified form.

Example 2

Find out the numerical projection of a → onto a straight line in the direction b → with a length a → equal to 8 and an angle between them of 60 degrees. By condition we have a ⇀ = 8, a ⇀, b → ^ = 60 °. So, let's substitute numeric values into the formula n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4 .

Answer: 4.

With known cos (a → , b → ^) = a ⇀ , b → a → · b → , we have a → , b → as the scalar product of a → and b → . Following from the formula n p b → a → = a → · cos a ⇀ , b → ^ , we can find the numerical projection a → directed along the vector b → and get n p b → a → = a → , b → b → . The formula is equivalent to the definition given at the beginning of the paragraph.

Definition 3

The numerical projection of the vector a → onto an axis coinciding in direction with b → is the ratio of the scalar product of the vectors a → and b → to the length b → . The formula n p b → a → = a → , b → b → is applicable to find the numerical projection of a → onto a line coinciding in direction with b → , with known a → and b → coordinates.

Example 3

Given b → = (- 3 , 4) . Find the numerical projection a → = (1, 7) onto L.

Solution

On the coordinate plane n p b → a → = a → , b → b → has the form n p b → a → = a → , b → b → = a x b x + a y b y b x 2 + b y 2 , with a → = (a x , a y ) and b → = b x , b y . To find the numerical projection of the vector a → onto the L axis, you need: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5.

Answer: 5.

Example 4

Find the projection of a → on L, coinciding with the direction b →, where there are a → = - 2, 3, 1 and b → = (3, - 2, 6). Three-dimensional space is specified.

Solution

Given a → = a x , a y , a z and b → = b x , b y , b z , we calculate the scalar product: a ⇀ , b → = a x · b x + a y · b y + a z · b z . The length b → is found using the formula b → = b x 2 + b y 2 + b z 2 . It follows that the formula for determining the numerical projection a → will be: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .

Substitute the numerical values: n p L a → = n p b → a → = (- 2) 3 + 3 (- 2) + 1 6 3 2 + (- 2) 2 + 6 2 = - 6 49 = - 6 7 .

Answer: - 6 7.

Let's look at the connection between a → on L and the length of the projection a → on L. Let's draw an axis L, adding a → and b → from a point on L, after which we draw a perpendicular line from the end a → to L and draw a projection onto L. There are 5 variations of the image:

First the case with a → = n p b → a → → means a → = n p b → a → → , hence n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → a → → .

Second the case implies the use of n p b → a → ⇀ = a → · cos a → , b → , which means n p b → a → = a → · cos (a → , b →) ^ = n p b → a → → .

Third the case explains that when n p b → a → → = 0 → we obtain n p b ⇀ a → = a → · cos (a → , b → ^) = a → · cos 90 ° = 0 , then n p b → a → → = 0 and n p b → a → = 0 = n p b → a → → .

Fourth the case shows n p b → a → → = a → · cos (180 ° - a → , b → ^) = - a → · cos (a → , b → ^) , follows n p b → a → = a → · cos (a → , b → ^) = - n p b → a → → .

Fifth the case shows a → = n p b → a → → , which means a → = n p b → a → → , hence we have n p b → a → = a → · cos a → , b → ^ = a → · cos 180° = - a → = - n p b → a → .

Definition 4

The numerical projection of the vector a → onto the L axis, which is directed in the same way as b →, has the following value:

the length of the projection of the vector a → onto L, provided that the angle between a → and b → is less than 90 degrees or equal to 0: n p b → a → = n p b → a → → with the condition 0 ≤ (a → , b →) ^< 90 ° ;
zero provided that a → and b → are perpendicular: n p b → a → = 0, when (a → , b → ^) = 90 °;
the length of the projection a → onto L, multiplied by -1, when there is an obtuse or straight angle of the vectors a → and b →: n p b → a → = - n p b → a → → with the condition of 90 °< a → , b → ^ ≤ 180 ° .

Example 5

Given the length of the projection a → onto L, equal to 2. Find the numerical projection a → provided that the angle is 5 π 6 radians.

Solution

From the condition it is clear that this angle is obtuse: π 2< 5 π 6 < π . Тогда можем найти числовую проекцию a → на L: n p L a → = - n p L a → → = - 2 .

Answer: - 2.

Example 6

Given a plane O x y z with a vector length a → equal to 6 3, b → (- 2, 1, 2) with an angle of 30 degrees. Find the coordinates of the projection a → onto the L axis.

Solution

First, we calculate the numerical projection of the vector a →: n p L a → = n p b → a → = a → · cos (a → , b →) ^ = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .

By condition, the angle is acute, then the numerical projection a → = the length of the projection of the vector a →: n p L a → = n p L a → → = 9. This case shows that the vectors n p L a → → and b → are co-directed, which means there is a number t for which the equality is true: n p L a → → = t · b → . From here we see that n p L a → → = t · b → , which means we can find the value of the parameter t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .

Then n p L a → → = 3 · b → with the coordinates of the projection of vector a → onto the L axis equal to b → = (- 2 , 1 , 2) , where it is necessary to multiply the values by 3. We have n p L a → → = (- 6 , 3 , 6) . Answer: (- 6, 3, 6).

It is necessary to repeat the previously learned information about the condition of collinearity of vectors.

If you notice an error in the text, please highlight it and press Ctrl+Enter

Algebraic projection of a vector on any axis is equal to the product of the length of the vector and the cosine of the angle between the axis and the vector:

Pr a b = |b|cos(a,b) or

Where a b is the scalar product of vectors, |a| - modulus of vector a.

Instructions. To find the projection of the vector Pr a b online, you must specify the coordinates of vectors a and b. In this case, the vector can be specified on the plane (two coordinates) and in space (three coordinates). The resulting solution is saved in a Word file. If vectors are specified through the coordinates of points, then you need to use this calculator.

Classification of vector projections

Types of projections by definition vector projection

The geometric projection of the vector AB onto the axis (vector) is called the vector A"B", the beginning of which A' is the projection of the beginning A onto the axis (vector), and the end B' is the projection of the end B onto the same axis.
The algebraic projection of the vector AB onto the axis (vector) is called the length of the vector A"B", taken with a + or - sign, depending on whether the vector A"B" has the same direction as the axis (vector).

Types of projections according to the coordinate system

Vector Projection Properties

The geometric projection of a vector is a vector (has a direction).
The algebraic projection of a vector is a number.

Vector projection theorems

Theorem 1. The projection of the sum of vectors onto any axis is equal to the projection of the summands of the vectors onto the same axis.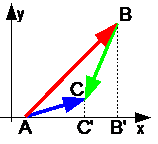

AC" =AB" +B"C"

Theorem 2. The algebraic projection of a vector onto any axis is equal to the product of the length of the vector and the cosine of the angle between the axis and the vector:

Pr a b = |b|·cos(a,b)

Types of vector projections

projection onto the OX axis.
projection onto the OY axis.
projection onto a vector.

Projection on the OX axis	Projection on the OY axis	Projection to vector
If the direction of vector A’B’ coincides with the direction of the OX axis, then the projection of vector A’B’ has a positive sign.	If the direction of the vector A’B’ coincides with the direction of the OY axis, then the projection of the vector A’B’ has a positive sign.	If the direction of vector A’B’ coincides with the direction of vector NM, then the projection of vector A’B’ has a positive sign.
If the direction of the vector is opposite to the direction of the OX axis, then the projection of the vector A’B’ has a negative sign.	If the direction of vector A’B’ is opposite to the direction of the OY axis, then the projection of vector A’B’ has a negative sign.	If the direction of vector A’B’ is opposite to the direction of vector NM, then the projection of vector A’B’ has a negative sign.
If vector AB is parallel to the OX axis, then the projection of vector A’B’ is equal to the absolute value of vector AB.	If vector AB is parallel to the OY axis, then the projection of vector A’B’ is equal to the absolute value of vector AB.	If vector AB is parallel to vector NM, then the projection of vector A’B’ is equal to the absolute value of vector AB.
If the vector AB is perpendicular to the axis OX, then the projection A’B’ is equal to zero (null vector).	If the vector AB is perpendicular to the OY axis, then the projection A’B’ is equal to zero (null vector).	If the vector AB is perpendicular to the vector NM, then the projection A’B’ is equal to zero (null vector).

1. Question: Can the projection of a vector have a negative sign? Answer: Yes, the projection vector can be a negative value. In this case, the vector has the opposite direction (see how the OX axis and the AB vector are directed)
2. Question: Can the projection of a vector coincide with the absolute value of the vector? Answer: Yes, it can. In this case, the vectors are parallel (or lie on the same line).
3. Question: Can the projection of a vector be equal to zero (null vector). Answer: Yes, it can. In this case, the vector is perpendicular to the corresponding axis (vector).

Example 1. The vector (Fig. 1) forms an angle of 60° with the OX axis (it is specified by vector a). If OE is a scale unit, then |b|=4, so .

Indeed, the length of the vector ( geometric projection b) is equal to 2, and the direction coincides with the direction of the OX axis.

Example 2. The vector (Fig. 2) forms an angle (a,b) = 120 o with the OX axis (with vector a). Length |b| vector b is equal to 4, so pr a b=4·cos120 o = -2.

Indeed, the length of the vector is 2, and the direction is opposite to the direction of the axis.

Projection vector onto an axis is a vector that is obtained by multiplying the scalar projection of a vector onto this axis and the unit vector of this axis. For example, if a x – scalar projection vector A to the X axis, then a x i- its vector projection onto this axis.

Let's denote vector projection the same as the vector itself, but with the index of the axis on which the vector is projected. So, the vector projection of the vector A on the X axis we denote A x ( fat a letter denoting a vector and a subscript of the axis name) or (a non-bold letter denoting a vector, but with an arrow at the top (!) and a subscript of the axis name).

Scalar projection vector per axis is called number, the absolute value of which is equal to the length of the axis segment (on the selected scale) enclosed between the projections of the start point and the end point of the vector. Usually instead of the expression scalar projection they simply say - projection. The projection is denoted by the same letter as the projected vector (in normal, non-bold writing), with a lower index (as a rule) of the name of the axis on which this vector is projected. For example, if a vector is projected onto the X axis A, then its projection is denoted by a x. When projecting the same vector onto another axis, if the axis is Y, its projection will be denoted a y.

To calculate the projection vector on an axis (for example, the X axis), it is necessary to subtract the coordinate of the starting point from the coordinate of its end point, that is
a x = x k − x n.
The projection of a vector onto an axis is a number. Moreover, the projection can be positive if the value x k is greater than the value x n,

negative if the value x k is less than the value x n

and equal to zero if x k equals x n.

The projection of a vector onto an axis can also be found by knowing the modulus of the vector and the angle it makes with this axis.

From the figure it is clear that a x = a Cos α

that is, the projection of the vector onto the axis is equal to the product of the modulus of the vector and the cosine of the angle between the direction of the axis and vector direction. If the angle is acute, then
Cos α > 0 and a x > 0, and, if obtuse, then the cosine of the obtuse angle is negative, and the projection of the vector onto the axis will also be negative.

Angles measured from the axis counterclockwise are considered positive, and angles measured along the axis are negative. However, since cosine is an even function, that is, Cos α = Cos (− α), when calculating projections, angles can be counted both clockwise and counterclockwise.

To find the projection of a vector onto an axis, the modulus of this vector must be multiplied by the cosine of the angle between the direction of the axis and the direction of the vector.

Vector coordinates— coefficients of the only possible linear combination of basis vectors in the selected coordinate system, equal to the given vector.

where are the coordinates of the vector.

Scalar product vectors

Scalar product of vectors[- in finite-dimensional vector space is defined as the sum of the products of identical components being multiplied vectors.

For example, S.p.v. a = (a 1 , ..., a n) And b = (b 1 , ..., b n):

(a , b ) = a 1 b 1 + a 2 b 2 + ... + a n b n