What is an equation?

Those who are taking their first steps in algebra, of course, require the most ordered presentation of the material. Therefore, in our article about what an equation is, we will not only give a definition, but also give various classifications of equations with examples.

What is an equation: general concepts

So, an equation is a type of equality with an unknown, denoted by a Latin letter. In this case, the numerical value of this letter, which allows us to obtain the correct equality, is called the root of the equation. You can read more about this in our article, but we will continue to talk about the equations themselves. The arguments of an equation (or variables) are unknowns, and the solution to an equation is finding all its roots or the absence of roots.

Types of equations

Equations are divided into two large groups: algebraic and transcendental.

• An algebraic equation is one in which only algebraic operations are used to find the root of the equation - 4 arithmetic ones, as well as exponentiation and extraction of the natural root.
• A transcendental equation is an equation in which non-algebraic functions are used to find the root: for example, trigonometric, logarithmic and others.

Among the algebraic equations there are also:

• integers - with both parts consisting of whole algebraic expressions in relation to unknowns;
• fractional - containing integer algebraic expressions in the numerator and denominator;
• irrational - algebraic expressions here are under the root sign.

Note also that fractional and irrational equations can be reduced to solving entire equations.

Transcendental equations are divided into:

• Exponential equations are equations that contain a variable as an exponent. They are solved by moving to a single base or exponent, taking the common factor out of brackets, factoring, and some other methods;
• logarithmic - equations with logarithms, that is, equations where the unknowns are inside the logarithms themselves. Solving such equations is very difficult (unlike, say, most algebraic ones), since this requires solid mathematical training. The most important thing here is to move from an equation with logarithms to an equation without them, that is, to simplify the equation (this method of removing logarithms is called potentiation). Of course, it is possible to potentiate a logarithmic equation only if they have identical numerical bases and do not have coefficients;
• trigonometric equations are equations with variables under the signs of trigonometric functions. Their solution requires initial mastery of trigonometric functions;
• mixed are differentiated equations with parts belonging to different types (for example, with parabolic and elliptic parts or elliptic and hyperbolic, etc.).

As for the classification by the number of unknowns, everything is simple: equations with one, two, three, and so on unknowns are distinguished. There is also another classification, which is based on the degree that is on the left side of the polynomial. Based on this, linear, quadratic and cubic equations are distinguished. Linear equations can also be called equations of the 1st degree, quadratic - 2nd, and cubic, respectively, 3rd. Well, now let’s give examples of equations of one group or another.

Examples of different types of equations

Examples of algebraic equations:

• ax + b= 0
• ax 3 + bx 2 + cx+ d= 0
• ax 4 + bx 3 + cx 2 + bx + a= 0
  (a is not equal to 0)

Examples of transcendental equations:

• cos x = x log x = x−5 2 x = logx+x 5 +40

Examples of whole equations:

• (2+x)2 = (2+x)(55x-4) (x2-12x+10)4 = (3x+10)4 (4x2+3x-10)2=9x4

Example of fractional equations:

• 15 x + — = 5x - 17 x

Example of irrational equations:

• √2kf(x)=g(x)

Examples of linear equations:

• 2x+7=0 x - 3 = 2 - 4x 2x+3=5x+5 - 3x - 2

Examples of quadratic equations:

• x 2 +5x−7= 0 3x 2 +5x−7= 0 11x 2 −7x+3 = 0

Examples of cubic equations:

• x 3 -9x 2 -46x+120=0 x 3 - 4x 2 + x + 6 = 0

Examples of exponential equations:

• 5 x+2 = 125 3 x 2 x = 8 x+3 3 2x +4 3 x -5 = 0

Examples of logarithmic equations:

• log 2 x= 3 log 3 x= -1

Examples of trigonometric equations:

• 3sin 2 x + 4sin x cosx + cos 2 x = 2 sin(5x+π/4) = ctg(2x-π/3) sinx + cos 2 x + tan 3 x = ctg 4 x

Examples of mixed equations:

• log x (log 9 (4⋅3 x −3))=1 |5x−8|+|2⋅5x+3|=13

It remains to add that a variety of methods are used to solve equations of various types. Well, in order to solve almost any equations, you will need knowledge not only of algebra, but also of trigonometry, and often very deep knowledge.

Mathematics. Algebra. Geometry. Trigonometry

ALGEBRA: Equations and systems of equations

4.2. Types of equations and methods for solving them

In the case when it is necessary to find the values ​​of a variable that satisfy both given equations, we say that it is given, system of equations. A curly brace is used to indicate a system:

Several equations with one variable form set of equations, if the task is to find all such values ​​of a variable, each of which is the root of at least one of these equations. A square bracket is used to indicate a population:

Equations containing a variable under the modulus sign.

The absolute value of a number A is defined as follows:

Example: Solve the equation

.

Solution: If

, That . You can write it like this:

From Eq.

we find X= -9. However, with this value of the variable, the inequality does not hold, which means that the value found is not the root of this equation., That and this equation will take the form. You can write it like this:

From Eq.

we find . The inequality is true, which means - the root of this equation..

Equations with a variable in the denominator.

Consider equations of the form

. (1)

The solution to an equation of type (1) is based on the following statement: a fraction is equal to 0 if and only if its numerator is equal to 0 and its denominator is non-zero.

In accordance with the above, the solution to the equation

is carried out in two stages: first you need to solve the equation, and then find out whether, with the found values ​​of the variable, X denominator at 0. If q(x) ¹ 0 , then the found root of the equationis also the root of equation (1); Ifq(x) = 0, then the resulting root of the equationis also the root of equation (1). The resulting system is:

Domain of the equation

f(x) = g(x) call the set of all those values ​​of a variable X, for which the expressionf(x), and the expression g(x)make sense.

If in the process of transforming an equation its domain of definition has expanded, then extraneous roots may appear. Therefore, all found values ​​of the variable must be checked by substitution into the original equation or using the domain of definition of the original equation.

Rational equations.

The equation

f(x) = g(x) called rational, If f(x) and g(x)-rational expressions. Moreover, if f(x) and g(x)- whole expressions, then the equation is called whole ;if at least one of the expressionsf(x), g(x)is fractional, then the rational equationf(x) = g(x) called fractional .

To solve a rational equation, you need:

1. find the common denominator of all available fractions;
2. replace this equation with a whole one, multiplying both its parts by a common denominator;
3. Solve the resulting whole equation;
4. Eliminate from its roots those that make the common denominator vanish.

Solving the equation

p(x) = 0 factorization method. p(x) can be factorized: , then the equation takes the form . If A- root of the equation, That , therefore at least one of the numbersequals 0.

The opposite is also true: if X

= A- the root of at least one of the equations , , , That A- root of the equation. That is

Solving equations

by introducing a new variable.

Let us explain the essence of the method with an example.

Example: Solve the equation

.

Solution. Let us put

, we get the equation, where we find . The problem comes down to solving a set of equations

Û

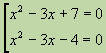
The first quadratic equation has no real roots, so its discriminant is negative. From the second we find

. These are the roots of the given equation.

An equation of the form is called biquadratic

, Where A ¹ 0. The biquadratic equation is solved by introducing a new variable: putting , we arrive at the quadratic equation .

Irrational equations.

Irrational

An equation is called in which the variable is contained under the sign of the root or under the sign of raising to a fractional power. One method for solving such equations is the method of raising both sides of the equation to the same power:

A) transform the given irrational equation to the form:

;

B) we raise both sides of the resulting equation to

n-th degree:

;

B) considering that

, we get the equation

f(x) = g(x);

)We solve the equation and do a check, since raising both sides of the equation to an even power can lead to the appearance of extraneous roots. This check is carried out by substituting the found values ​​of the variable into the original equation.

Copyright © 2005-2013 Xenoid v2.0

Use of site materials is possible subject to an active link.

Maintaining your privacy is important to us. For this reason, we have developed a Privacy Policy that describes how we use and store your information. Please review our privacy practices and let us know if you have any questions.

Collection and use of personal information

Personal information refers to data that can be used to identify or contact a specific person.

You may be asked to provide your personal information at any time when you contact us.

Below are some examples of the types of personal information we may collect and how we may use such information.

What personal information do we collect:

• When you submit an application on the site, we may collect various information, including your name, phone number, email address, etc.

How we use your personal information:

• The personal information we collect allows us to contact you with unique offers, promotions and other events and upcoming events.
• From time to time, we may use your personal information to send important notices and communications.
• We may also use personal information for internal purposes, such as conducting audits, data analysis and various research in order to improve the services we provide and provide you with recommendations regarding our services.
• If you participate in a prize draw, contest or similar promotion, we may use the information you provide to administer such programs.

Disclosure of information to third parties

We do not disclose the information received from you to third parties.

Exceptions:

• If necessary - in accordance with the law, judicial procedure, in legal proceedings, and/or on the basis of public requests or requests from government bodies in the Russian Federation - to disclose your personal information. We may also disclose information about you if we determine that such disclosure is necessary or appropriate for security, law enforcement, or other public importance purposes.
• In the event of a reorganization, merger, or sale, we may transfer the personal information we collect to the applicable successor third party.

Protection of personal information

We take precautions - including administrative, technical and physical - to protect your personal information from loss, theft, and misuse, as well as unauthorized access, disclosure, alteration and destruction.

Respecting your privacy at the company level

To ensure that your personal information is secure, we communicate privacy and security standards to our employees and strictly enforce privacy practices.

Types of algebraic equations and methods for solving them

For students interested in mathematics, when solving algebraic equations of higher degrees, an effective method for quickly finding roots, dividing with a remainder by the binomial x -  or by ax + b, is the Horner scheme.

Consider Horner's scheme.

Let us denote the incomplete quotient when dividing P(x) by x –  through

Q (x) = b 0 x n -1 + b 1 x n -2 + ... + b n -1, and the remainder is b n.

Since P(x) = Q (x)(x–) + b n, then the equality holds

a 0 x n + а 1 x n -1 + … + а n = (b 0 x n -1 + b 1 x n -2 + … + b n -1)(х– ) + b n

Let's open the brackets on the right side and compare the coefficients for the same powers of x on the left and right. We obtain that a 0 = b 0 and for 1  k  n the relations a k = b k -  b k -1 hold. It follows that b 0 = a 0 and b k = a k +  b k -1, 1  k  n.

We write the calculation of the coefficients of the polynomial Q (x) and the remainder b n in the form of a table:

a 0

a 1

a 2

A n-1

A n

b 0 = a 0

b 1 = a 1 +  b 0

b 2 = a 2 +  b 1

b n-1 = a n-1 +  b n-2

b n = a n +  b n-1

Example 1. Divide the polynomial 2x 4 – 7x 3 – 3x 2 + 5x – 1 by x + 1.

Solution. We use Horner's scheme.

When dividing 2x 4 – 7x 3 – 3x 2 + 5x – 1 by x + 1 we get 2x 3 – 9x 2 + 6x – 1

Answer: 2 x 3 – 9x 2 + 6x – 1

Example 2. Calculate P(3), where P(x) = 4x 5 – 7x 4 + 5x 3 – 2x + 1

Solution. Using Bezout's theorem and Horner's scheme, we obtain:

Answer: P(3) = 535

Exercise

Using Horner's diagram, divide the polynomial

4x 3 – x 5 + 132 – 8x 2 on x + 2;

2) Divide the polynomial

2x 2 – 3x 3 – x + x 5 + 1 on x + 1;

3) Find the value of the polynomial P 5 (x) = 2x 5 – 4x 4 – x 2 + 1 for x = 7.

1.1. Finding rational roots of equations with integer coefficients

The method for finding rational roots of an algebraic equation with integer coefficients is given by the following theorem.

Theorem: If an equation with integer coefficients has rational roots, then they are the quotient of dividing the divisor of the free term by the divisor of the leading coefficient.

Proof: a 0 x n + a 1 x n -1 + … + a n = 0

Let x = p/ q is a rational root, q, p are coprime.

Substituting the fraction p/q into the equation and freeing ourselves from the denominator, we get

a 0 r n + a 1 p n -1 q + … + a n -1 pq n -1 + a n q n = 0 (1)

Let's rewrite (1) in two ways:

a n q n = р(– а 0 р n -1 – а 1 р n -2 q – … – а n -1 q n -1) (2)

a 0 r n = q (– а 1 р n -1 –… – а n -1 рq n -2 – а n q n -1) (3)

From equality (2) it follows that a n q n is divisible by p, and since q n and p are coprime, then a n is divisible by p. Similarly, from equality (3) it follows that a 0 is divisible by q. The theorem has been proven.

Example 1. Solve the equation 2x 3 – 7x 2 + 5x – 1 = 0.

Solution. The equation does not have integer roots; we find the rational roots of the equation. Let the irreducible fraction p /q be the root of the equation, then p is found among the divisors of the free term, i.e. among the numbers  1, and q among the positive divisors of the leading coefficient: 1; 2.

Those. rational roots of the equation must be sought among the numbers  1,  1/2, denote P 3 (x) = 2x 3 – 7x 2 + 5x – 1, P 3 (1)  0, P 3 (–1)  0,

P 3 (1/2) = 2/8 – 7/4 + 5/2 – 1 = 0, 1/2 is the root of the equation.

2x 3 – 7x 2 + 5x – 1 = 2x 3 – x 2 – 6 x 2 + 3x + 2x – 1 = 0.

We get: x 2 (2x – 1) – 3x (2x – 1)+ (2x – 1) = 0; (2x – 1)(x 2 – 3x + 1) = 0.

Equating the second factor to zero and solving the equation, we get

Answer:
,

Exercises

Solve equations:

6x 3 – 25x 2 + 3x + 4 = 0;

6x 4 – 7x 3 – 6x 2 + 2x + 1 = 0;

3x 4 – 8x 3 – 2x 2 + 7x – 1 = 0;

1.2. Reciprocal equations and solution methods

Definition. An equation with integer powers with respect to an unknown is called recurrent if its coefficients, equidistant from the ends of the left side, are equal to each other, i.e. equation of the form

A x n + bx n -1 + cx n -2 + … + cx 2 + bx + a = 0

Reciprocal equation of odd degree

A x 2 n +1 + bx 2 n + cx 2 n -1 + … + cx 2 + bx + a = 0

always has a root x = – 1. Therefore, it is equivalent to combining the equation x + 1 = 0 and  x 2 n +  x 2 n -1 + … +  x +  = 0. The last equation is a reciprocal equation of even degree. Thus, solving reciprocal equations of any degree is reduced to solving a reciprocal equation of even degree.

How to solve it? Let a reciprocal equation of even degree be given

A x 2 n + bx 2 n -1 + … + dx n +1 + ex n + dx n -1 + … + bx + a = 0

Note that x = 0 is not a root of the equation. Then we divide the equation by x n, we get

A x n + bx n -1 + … + dx + e + dx -1 + … + bx 1- n + аx -n = 0

We group the terms of the left side in pairs

A( x n + x - n ) + b (x n -1 + x -(n -1) + … + d(x + x -1 ) + e = 0

We make the replacement x + x -1 = y. After substituting the expressions x 2 + x -2 = y 2 – 2;

x 3 + x -3 = y 3 – 3y; x 4 + x -4 = y 4 – 4y + 2 into the equation we get the equation for atАу n + By n -1 +Cy n -2 + … + Ey + D = 0.

To solve this equation, you need to solve several quadratic equations of the form x + x -1 = y k, where k = 1, 2, ... n. Thus, we obtain the roots of the original equation.

Example 1. Solve the equation x 7 + x 6 – 5x 5 – 13x 4 – 13x 3 – 5x 2 + 2x + 1 = 0.

Solution. x = – 1 is the root of the equation. Let's apply Horner's scheme.

Our equation will take the form:

(x + 1)(x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1) = 0

1) x + 1 = 0, x = -1;

2) x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1 = 0 | : x 3  0; x 3 + x 2 – 6x – 7 – 6/x + 1/x 2 + 1/x 3 =0.

Grouping, we get: .

Let's introduce a replacement:
;
;
.

We get relatively at equation: y 3 – 3y + y 2 – 2 – 6y – 7 = 0;

y 3 + y 2 – 9y – 9 = 0; y 2 (y + 1) – 9 (y + 1) = 0; (y + 1)(y 2 – 9); y 1 = -1, y 2,3 =  3.

Solving equations
,
,
,

we get the roots:
,
,
,

Answer: x 1 = -1,
,

Exercises

Solve equations.

2x 5 + 5x 4 – 13x 3 – 13x 2 + 5x + 2 = 0;

2x 4 + 3x 3 – 16x 2 + 3x + 2 = 0;

15x 5 + 34x 4 + 15x 3 – 15x 2 – 34x – 15 = 0.

1.3. Variable replacement method for solving equations

The variable replacement method is the most common method. The art of making a variable change is to see which change makes the most sense and will lead to success more quickly.

If given the equation

F(f(x)) = 0, (1)

then by replacing the unknown y = f (x) it is first reduced to the equation

F(y) = 0, (2)

and then after finding all the solutions to equation (2) y 1, y 2, ..., y n, ... is reduced to solving the set of equations f (x) = y 1, f (x) = y 2,..., f (x) = y 2,...

The main ways to implement the variable replacement method are:

using the basic property of a fraction;

highlighting the square of the binomial;

transition to a system of equations;

opening brackets in pairs;

opening parentheses in pairs and dividing both sides of the equation;

decreasing the degree of the equation;

double replacement.

1.3.1. Reducing the power of an equation

Solve the equation (x 2 + x + 2)(x 2 + x + 3) = 6 (3)

Solution. Let's denote x 2 + x + 2 = y, then let's take y (y + 1) = 6, solving the latter, we get y 1 = 2, y 2 = -3. This equation (3) is equivalent to the set of equations x 2 + x + 2 = 2

x 2 + x + 2 = -3

Solving the first, we get x 1 = 0, x 2 = -1. Solving the second, we get
,

Answer: x 1 = 0, x 2 = -1,

1.3.2. Fourth degree equation of the form (x + a)(x +b )(x + c )(x + d ) = m , where a + b = c + d, or a + c = b + d, or a + d = b + c.

Example. Solve the equation (x - 1)(x - 7)(x -4)(x + 2) = 40

Solution. – 1- 4 = - 7 + 2, - 5 = - 5, multiplying these pairs of brackets, we get the equation (x 2 - 5x - 14)(x 2 - 5x + 4) = 40

Let's introduce the replacement: x 2 - 5x – 14 = y, we get the equation y(y + 18) = 40, y 2 + 18y = 40, y 2 + 18y – 40 = 0. y 1 = -20, y 2 = 2. Returning to the original variable, we solve a set of equations:

X 2 - 5x – 14 = - 20 x 1 = 2; x 2 = 3

x 2 - 5x – 14 = 2 x 3.4 =

Answer: x 1 = 2; x 2 = 3 x 3.4 =

1.3.3. An equation of the form (x + a)(x + b)(x + c)(x + d) = Ex 2,

Where ab = cd, or ac =bd, or ad = bc. Open the brackets in pairs and divide both parts by x 2  0.

Example. (x - 1)(x - 2)(x - 8)(x - 4) = 4x 2

Solution. The product of the numbers in the first and third and in the second and fourth brackets are equal, i.e. – 8 (- 1) = (- 2)(- 4). Let's multiply the indicated pairs of brackets and write the equation (x 2 - 9x + 8)(x 2 - 6x + 8) = 4x 2.

Since x = 0 is not a root of the equation, we divide both sides of the equation by x 2  0, we get:
, replacement:
, the original equation will take the form:t(t+3) =4, t 2 + 3 t=4, t 2 + 3 t – 4=0, t 1 =1, t 2 = - 4.

Let's return to the original variable:

x 2 - 10x + 8 = 0

x 2 - 5x + 8 = 0

We solve the first equation, we get x 1,2 = 5 

The second equation has no roots.

Answer: x 1.2 = 5 

1.3.4. Equation of the fourth type (ax 2 + b 1 x + c)(a x 2 + b 2 x + c) = A x 2

Equation (ax 2 + b 1 x+ c)(a x 2 + b 2 x + c) = A x 2, where c  0, A  2
, which after replacing the unknown
can be rewritten as a square and can be easily solved.

Example. (x 2 + x+ 2)(x 2 + 2x + 2) = 2x 2

Solution. It is easy to see that x = 0 is not a root of this equation by dividing this equation by x 2 , we get the equation

replacement
, we get the equation (y+1)(y+2) = 2, solving it, we have roots y 1 = 0; at 2 = - 3, therefore the original equation is equivalent to the set of equations

solving, we get x 1 = -1; x 2 = -2.

Answer: x 1 = -1; x 2 = -2

1.3.5. Equation of the form: a (cx 2 + p 1 x + q) 2 + b (cx 2 + p 2 x + q) 2 = Ax 2

The equation a(cx 2 + p 1 x + q) 2 + b(cx 2 + p 2 x + q) 2 = Ax 2 where a, b, c, q, A are such that q 0, A 0, c 0, a 0, b 0 has no root x = 0, so dividing the equation by x 2 , we obtain an equivalent equation
, which after replacement
can be rewritten as a quadratic equation that can be easily solved. + 1)( x 2 – 14x + 15 = 0

x 2 – 7 x + 15 = 0

Answer:

In some problems of physics, it is not possible to establish a direct connection between the quantities describing the process. But it is possible to obtain an equality containing the derivatives of the functions under study. This is how differential equations arise and the need to solve them to find an unknown function.

This article is intended for those who are faced with the problem of solving a differential equation in which the unknown function is a function of one variable. The theory is structured in such a way that with zero knowledge of differential equations, you can cope with your task.

Each type of differential equation is associated with a solution method with detailed explanations and solutions to typical examples and problems. All you have to do is determine the type of differential equation of your problem, find a similar analyzed example and carry out similar actions.

To successfully solve differential equations, you will also need the ability to find sets of antiderivatives (indefinite integrals) of various functions. If necessary, we recommend that you refer to the section.

First, we will consider the types of ordinary differential equations of the first order that can be resolved with respect to the derivative, then we will move on to second-order ODEs, then we will dwell on higher-order equations and end with systems of differential equations.

Recall that if y is a function of the argument x.

First order differential equations.

The simplest first order differential equations of the form.

Let's write down a few examples of such remote control .

Differential equations can be resolved with respect to the derivative by dividing both sides of the equality by f(x) . In this case, we arrive at an equation that will be equivalent to the original one for f(x) ≠ 0. Examples of such ODEs are .

If there are values ​​of the argument x at which the functions f(x) and g(x) simultaneously vanish, then additional solutions appear. Additional solutions to the equation given x are any functions defined for these argument values. Examples of such differential equations include:

Second order differential equations.

Linear homogeneous differential equations of the second order with constant coefficients.

LDE with constant coefficients is a very common type of differential equation. Their solution is not particularly difficult. First, the roots of the characteristic equation are found . For different p and q, three cases are possible: the roots of the characteristic equation can be real and different, real and coinciding or complex conjugates. Depending on the values ​​of the roots of the characteristic equation, the general solution of the differential equation is written as , or , or respectively.

For example, consider a linear homogeneous second-order differential equation with constant coefficients. The roots of its characteristic equation are k 1 = -3 and k 2 = 0. The roots are real and different, therefore, the general solution of the LODE with constant coefficients has the form


Linear inhomogeneous differential equations of the second order with constant coefficients.

The general solution of a second-order LDDE with constant coefficients y is sought in the form of the sum of the general solution of the corresponding LDDE and a particular solution to the original inhomogeneous equation, that is, . The previous paragraph is devoted to finding a general solution to a homogeneous differential equation with constant coefficients. And a particular solution is determined either by the method of indefinite coefficients for a certain form of the function f(x) on the right side of the original equation, or by the method of varying arbitrary constants.

As examples of second-order LDDEs with constant coefficients, we give


To understand the theory and get acquainted with detailed solutions of examples, we offer you on the page linear inhomogeneous second-order differential equations with constant coefficients.

Linear homogeneous differential equations (LODE) and linear inhomogeneous differential equations (LNDEs) of the second order.

A special case of differential equations of this type are LODE and LDDE with constant coefficients.

The general solution of the LODE on a certain segment is represented by a linear combination of two linearly independent partial solutions y 1 and y 2 of this equation, that is, .

The main difficulty lies precisely in finding linearly independent partial solutions to a differential equation of this type. Typically, particular solutions are selected from the following systems of linearly independent functions:


However, particular solutions are not always presented in this form.

An example of a LOD is .

The general solution of the LDDE is sought in the form , where is the general solution of the corresponding LDDE, and is the particular solution of the original differential equation. We just talked about finding it, but it can be determined using the method of varying arbitrary constants.

An example of LNDU can be given .

Differential equations of higher orders.

Differential equations that allow a reduction in order.

Order of differential equation , which does not contain the desired function and its derivatives up to k-1 order, can be reduced to n-k by replacing .

In this case, the original differential equation will be reduced to . After finding its solution p(x), it remains to return to the replacement and determine the unknown function y.

For example, the differential equation after the replacement, it will become an equation with separable variables, and its order will be reduced from third to first.