مجموع زاویه ها چقدر است؟ قضیه مجموع زوایای مثلث. انواع بر اساس اندازه زاویه

مجموع زوایای مثلث- مهم است، اما کافی است تم ساده، که در هندسه پایه هفتم تدریس می شود. موضوع شامل یک قضیه، یک اثبات کوتاه و چندین نتیجه منطقی است. دانستن این موضوع به حل کمک می کند مسائل هندسیدر طول مطالعه بعدی موضوع

قضیه - زوایای یک مثلث دلخواه با هم جمع شوند؟

این قضیه بیان می کند که اگر هر مثلثی را، صرف نظر از نوع آن، بگیرید، مجموع همه زوایا همیشه 180 درجه خواهد بود. این به صورت زیر ثابت می شود:

• به عنوان مثال، مثلث ABC را در نظر بگیرید، یک خط مستقیم از نقطه B واقع در راس بکشید و آن را به عنوان "a" تعیین کنید، خط مستقیم "a" کاملاً موازی با ضلع AC است.
• بین خط مستقیم "a" و اضلاع AB و BC، زوایا مشخص شده است و آنها را با اعداد 1 و 2 مشخص می کنند.
• زاویه 1 برابر با زاویه A در نظر گرفته می شود و زاویه 2 برابر با زاویه C در نظر گرفته می شود، زیرا این زاویه ها به صورت متقاطع در نظر گرفته می شوند.
• بنابراین، مجموع بین زوایای 1، 2 و 3 (که به جای زاویه B تعیین شده است) برابر با زاویه باز شده با راس B شناخته می شود - و 180 درجه است.

اگر مجموع زوایای نشان داده شده با اعداد 180 درجه باشد، مجموع زوایای A، B و C برابر با 180 درجه تشخیص داده می شود. این قانون برای هر مثلثی صادق است.

آنچه از قضیه هندسی بر می آید

مرسوم است که چندین نتیجه از قضیه فوق برجسته شود.

• اگر مسئله مثلثی با زاویه قائمه در نظر گرفته شود، یکی از زوایای آن به طور پیش فرض برابر با 90 درجه و مجموع زوایای تند نیز 90 درجه خواهد بود.
• اگر در مورد مثلث متساوی الساقین قائم الزاویه صحبت می کنیم، زوایای تند آن که مجموعاً 90 درجه است، به صورت جداگانه برابر با 45 درجه خواهد بود.
• یک مثلث متساوی الاضلاع به ترتیب از سه زاویه مساوی تشکیل شده است که هر یک از آنها برابر با 60 درجه و در مجموع 180 درجه خواهد بود.
• زاویه بیرونی هر مثلث برابر با مجموع دو زاویه داخلی است که مجاور آن نیستند.

قانون زیر را می توان استخراج کرد: هر مثلثی حداقل دو زاویه تند دارد. در برخی موارد، یک مثلث از سه زاویه تند تشکیل شده است و اگر فقط دو زاویه باشد، زاویه سوم منفرد یا قائم خواهد بود.

قضیه. مجموع زوایای داخلی یک مثلث برابر با دو زاویه قائمه است.

بیایید چند مثلث ABC را در نظر بگیریم (شکل 208). اجازه دهید زوایای داخلی آن را با اعداد 1، 2 و 3 نشان دهیم. اجازه دهید آن را ثابت کنیم

∠1 + ∠2 + ∠3 = 180 درجه.

اجازه دهید از میان برخی از راس مثلث، برای مثال B، یک خط مستقیم MN موازی با AC رسم کنیم.

در راس B سه زاویه داریم: ∠4، ∠2 و ∠5. مجموع آنها یک زاویه مستقیم است، بنابراین برابر با 180 درجه است:

∠4 + ∠2 + ∠5 = 180 درجه.

اما ∠4 = ∠1 زوایای متقاطع داخلی با خطوط موازی MN و AC و مقطع AB هستند.

∠5 = ∠3 - اینها زوایای متقاطع داخلی با خطوط موازی MN و AC و مقطع BC هستند.

این به این معنی است که ∠4 و ∠5 را می توان با معادل های ∠1 و ∠3 جایگزین کرد.

بنابراین، ∠1 + ∠2 + ∠3 = 180 درجه. قضیه ثابت شده است.

2. خاصیت زاویه خارجی مثلث.

در واقع در مثلث ABC (شکل 209) ∠1 + ∠2 = 180° - ∠3 و همچنین ∠ВСD، زاویه خارجی این مثلث، نه مجاور ∠1 و ∠2، نیز برابر با 180 درجه است. - ∠3.

بدین ترتیب:

∠1 + ∠2 = 180 درجه - ∠3;

∠BCD = 180 درجه - ∠3.

بنابراین، ∠1 + ∠2 = ∠BCD.

ویژگی مشتق شده از زاویه بیرونی یک مثلث، محتوای قضیه قبلاً اثبات شده را در مورد زاویه خارجی یک مثلث روشن می کند، که فقط بیان می کرد که زاویه بیرونی یک مثلث بزرگتر از هر زاویه داخلی مثلثی است که مجاور آن نیست. اکنون مشخص شده است که زاویه خارجی برابر است با مجموع هر دو زاویه داخلی که مجاور آن نیستند.

3. خاصیت مثلث قائم الزاویه با زاویه 30 درجه.

بگذارید زاویه B در مثلث قائم الزاویه ACB برابر با 30 درجه باشد (شکل 210). سپس زاویه حاد دیگر آن برابر با 60 درجه خواهد بود.

اجازه دهید ثابت کنیم که پای AC برابر با نیمی از هیپوتانوس AB است. بیایید پای AC را فراتر از راس زاویه راست C بکشیم و یک قطعه CM برابر با قطعه AC کنار بگذاریم. بیایید نقطه M را به نقطه B وصل کنیم. مثلث حاصل VСМ برابر با مثلث ACB است. می بینیم که هر زاویه از مثلث ABM برابر با 60 درجه است، بنابراین این مثلث یک مثلث متساوی الاضلاع است.

پای AC برابر با نصف AM است و از آنجایی که AM برابر با AB است، پای AC برابر با نیمی از هیپوتانوس AB خواهد بود.

مجموع زوایای داخلی یک مثلث 180 0 است. این یکی از بدیهیات اساسی هندسه اقلیدس است. این هندسه ای است که دانش آموزان مدرسه مطالعه می کنند. هندسه به عنوان علمی است که به بررسی اشکال فضایی جهان واقعی می پردازد.

انگیزه یونانیان باستان برای توسعه هندسه چیست؟ نیاز به اندازه گیری مزارع، مراتع - مناطقی از سطح زمین. در همان زمان، یونانیان باستان پذیرفتند که سطح زمین افقی و صاف است. با در نظر گرفتن این فرض، بدیهیات اقلیدس از جمله مجموع زوایای داخلی یک مثلث 180 0 ایجاد شد.

بدیهیات گزاره ای است که نیازی به اثبات ندارد. این را چگونه باید فهمید؟ آرزویی بیان می شود که مناسب شخص باشد و سپس با تصاویر تأیید می شود. اما هر چیزی که ثابت نشده است تخیلی است، چیزی که در واقعیت وجود ندارد.

با گرفتن سطح زمین به صورت افقی، یونانیان باستان به طور خودکار شکل زمین را مسطح می پذیرفتند، اما متفاوت است - کروی. هیچ صفحه افقی یا خطوط مستقیمی در طبیعت وجود ندارد، زیرا گرانش فضا را خم می کند. خطوط مستقیم و سطوح افقی فقط در مغز انسان یافت می شود.

بنابراین، هندسه اقلیدس، که اشکال فضایی دنیای داستانی را توضیح می‌دهد، شبیه‌سازی است - نسخه‌ای که اصل ندارد.

یکی از بدیهیات اقلیدس بیان می کند که مجموع زوایای داخلی یک مثلث 180 0 است. در واقع، در فضای منحنی واقعی، یا در سطح کروی زمین، مجموع زوایای داخلی یک مثلث همیشه بزرگتر از 180 0 است.

اینجوری فکر کنیم هر نصف النهار روی کره زمین با زاویه 90 0 با خط استوا تلاقی می کند. برای به دست آوردن مثلث، باید نصف النهار دیگری را از نصف النهار دور کنید. مجموع زوایای مثلث بین نصف النهارها و ضلع استوا 180 0 خواهد بود. اما همچنان یک زاویه در قطب وجود خواهد داشت. در نتیجه مجموع تمام زوایا بیش از 180 0 خواهد بود.

اگر اضلاع با زاویه 90 0 در قطب متقاطع شوند، مجموع زوایای داخلی چنین مثلثی 270 0 خواهد بود. دو نصف النهار که خط استوا را در زوایای قائم در این مثلث قطع می کنند با یکدیگر موازی می شوند و در قطبی که با زاویه 90 0 یکدیگر را قطع می کنند عمود خواهند شد. معلوم می شود که دو خط موازی در یک صفحه نه تنها همدیگر را قطع می کنند، بلکه می توانند در قطب نیز عمود باشند.

البته، اضلاع چنین مثلثی خطوط مستقیم نیستند، بلکه محدب هستند و شکل کروی را تکرار می کنند. کره زمین. اما این دقیقاً دنیای واقعی فضاست.

هندسه فضای واقعی با در نظر گرفتن انحنای آن در اواسط قرن نوزدهم. توسط ریاضیدان آلمانی B. Riemann (1820-1866) توسعه یافته است. اما به دانش آموزان مدرسه در این مورد گفته نمی شود.

بنابراین، هندسه اقلیدسی، که شکل زمین را به صورت مسطح با سطح افقی می گیرد، که در واقع اینطور نیست، یک شبیه ساز است. نوتیک هندسه ریمانی است که انحنای فضا را در نظر می گیرد. مجموع زوایای داخلی مثلث در آن بزرگتر از 180 0 است.

اثبات

اجازه دهید ABC" - مثلث دلخواه بیایید از طریق بالا رهبری کنیم ب خط موازی با خط A.C. (به چنین خط مستقیمی خط مستقیم اقلیدسی می گویند). بیایید یک نقطه روی آن علامت گذاری کنیم D به طوری که نقاطآ و D در طرف مقابل یک خط مستقیم دراز بکشید قبل از میلاد مسیح..زاویه DBCو ACBبرابر با دروغ متقاطع داخلی است که توسط یک سکونت تشکیل شده است قبل از میلاد مسیح.با خطوط موازی A.C.و BD. بنابراین مجموع زوایای یک مثلث در رئوس بو بابرابر با زاویه ABD.مجموع هر سه زاویه یک مثلث برابر است با مجموع زوایا ABDو BAC. از آنجایی که این زوایای داخلی یک طرفه برای موازی هستند A.C.و BDدر مقطع AB، سپس مجموع آنها 180 درجه است. قضیه ثابت شده است.

عواقب

از قضیه بر می آید که هر مثلثی دو زاویه تند دارد. در واقع، با استفاده از اثبات از طریق تضاد، فرض کنیم که مثلث فقط یک زاویه تند دارد یا اصلاً زاویه تند ندارد. سپس این مثلث حداقل دو زاویه دارد که هر کدام حداقل 90 درجه است. مجموع این زاویه ها کمتر از 180 درجه نیست. اما این غیر ممکن است، زیرا مجموع تمام زوایای یک مثلث 180 درجه است. Q.E.D.

تعمیم به نظریه سیمپلکس

زاویه بین وجه i و j سیمپلکس کجاست.

یادداشت

• در یک کره، مجموع زوایای یک مثلث همیشه از 180 درجه تجاوز می کند، به این اختلاف مازاد کروی می گویند و متناسب با مساحت مثلث است.
• در صفحه لوباچفسکی مجموع زوایای یک مثلث همیشه کمتر از 180 درجه است. این تفاوت نیز متناسب با مساحت مثلث است.

همچنین ببینید

بنیاد ویکی مدیا 2010.

ببینید «قضیه مجموع زوایای مثلث» در فرهنگ‌های دیگر چیست:

ویژگی چندضلعی ها در هندسه اقلیدسی: مجموع زوایای n یک مثلث 180 درجه (n 2) است. مطالب 1 اثبات 2 نکته ... ویکی پدیا

قضیه فیثاغورث یکی از قضایای اساسی هندسه اقلیدسی است که رابطه بین اضلاع یک مثلث قائم الزاویه را برقرار می کند. مطالب 1 ... ویکی پدیا

قضیه فیثاغورث یکی از قضایای اساسی هندسه اقلیدسی است که رابطه بین اضلاع یک مثلث قائم الزاویه را برقرار می کند. مطالب 1 بیانیه 2 شواهد ... ویکی پدیا

قضیه کسینوس تعمیم قضیه فیثاغورث است. مربع یک ضلع مثلث برابر است با مجموع مربعات دو ضلع دیگر آن بدون اینکه دو برابر حاصل ضرب این ضلع ها در کسینوس زاویه بین آنها باشد. برای یک مثلث صفحه با اضلاع a,b,cو زاویه α... ... ویکی پدیا

این اصطلاح معانی دیگری دارد، مثلث (معانی) را ببینید. مثلث (در فضای اقلیدسی) است شکل هندسی، توسط سه بخش تشکیل شده است که سه نقطه را که روی یک خط مستقیم قرار ندارند به هم متصل می کند. سه نقطه،... ... ویکی پدیا

نماد استاندارد مثلث ساده ترین چند ضلعی است که دارای 3 راس (زاویه) و 3 ضلع است. بخشی از صفحه که توسط سه نقطه محدود شده است که روی یک خط قرار ندارند و سه بخش که این نقاط را به صورت جفت به هم متصل می کنند. رئوس مثلث ... ویکی پدیا

ریاضیدان یونان باستان. در قرن سوم در اسکندریه کار کرد. قبل از میلاد مسیح ه. اثر اصلی "Principia" (15 کتاب)، شامل مبانی ریاضیات باستان، هندسه ابتدایی، نظریه اعداد، نظریه عمومیروابط و روش های تعیین مساحت و حجم،... ... فرهنگ لغت دایره المعارفی

- (متوفی بین 275 تا 270 قبل از میلاد) ریاضیدان یونان باستان. اطلاعاتی از زمان و مکان تولد او به دست ما نرسیده است، اما معلوم است که اقلیدس در اسکندریه زندگی می کرد و اوج فعالیت او در زمان سلطنت بطلمیوس اول در مصر اتفاق افتاد... ... فرهنگ لغت دایره المعارفی بزرگ

هندسه شبیه هندسه اقلیدسی است که حرکت ارقام را تعریف می کند، اما با هندسه اقلیدسی تفاوت دارد زیرا یکی از پنج اصل آن (دوم یا پنجم) با نفی آن جایگزین می شود. نفی یکی از فرضیه های اقلیدسی... ... دایره المعارف کولیر

مثلث . مثلث حاد، منفرد و قائم الزاویه.

پاها و هیپوتانوز. مثلث متساوی الساقین و متساوی الاضلاع.

مجموع زوایای یک مثلث

زاویه خارجی مثلث نشانه های تساوی مثلث ها.

خطوط و نقاط قابل توجه در یک مثلث: ارتفاع، میانه،

نیمساز، میانهه عمود، عمود مرکز،

مرکز ثقل، مرکز دایره محصور، مرکز دایره محاطی.

قضیه فیثاغورس. نسبت ابعاد در یک مثلث دلخواه.

مثلث چند ضلعی با سه ضلع (یا سه زاویه) است. اضلاع یک مثلث اغلب با حروف کوچکی که مربوط به حروف بزرگ نشان دهنده رئوس مخالف هستند نشان داده می شوند.

اگر هر سه زاویه حاد هستند (شکل 20)، پس این مثلث حاد . اگر یکی از زوایا راست باشد(C، شکل 21)، به این معنا که راست گوشه; طرفینالف، بتشکیل یک زاویه قائمه نامیده می شود پاها; سمتجمقابل زاویه راست نامیده می شود هیپوتنوئوس. اگر یکی اززوایای منفرد (B، شکل 22)، به این معنا که مثلث منفرد


مثلث ABC (شکل 23) - متساوی الساقین، اگر دواضلاع آن برابر است (آ= ج) این اضلاع مساوی نامیده می شوند جانبی، شخص ثالث نامیده می شود اساسمثلث. مثلث ABC (شکل 24) - متساوی الاضلاع, اگر همهاضلاع آن برابر است (آ = ب = ج). به طور کلی ( آ ≠ ب ≠ ج) ما داریم scaleneمثلث .

ویژگی های اساسی مثلث ها در هر مثلث:

1. در مقابل ضلع بزرگتر زاویه بزرگتر قرار دارد و بالعکس.

2. زوایای مساوی در مقابل اضلاع مساوی قرار دارند و بالعکس.

به طور خاص، تمام زوایای در متساوی الاضلاعمثلث برابر هستند

3. مجموع زوایای یک مثلث 180 است º .

از دو ویژگی آخر چنین برمی‌آید که هر زاویه در متساوی الاضلاع است

مثلث 60 است º.

4. ادامه یکی از اضلاع مثلث (AC، شکل 25)، ما گرفتیم خارجی

زاویه BCD . زاویه خارجی یک مثلث برابر است با مجموع زوایای داخلی

در مجاورت آن نیست : BCD = A + B.

5. هر ضلع مثلث کوچکتر از مجموع دو ضلع دیگر و بزرگتر است

تفاوت های آنها (آ < ب + ج, آ > ب – ج;ب < آ + ج, ب > آ – ج;ج < آ + ب,ج > آ – ب).

نشانه های تساوی مثلث ها.

مثلث ها همسان هستند اگر به ترتیب برابر باشند:

آ ) دو ضلع و زاویه بین آنها.

ب ) دو گوشه و ضلع مجاور آنها.

ج) سه طرف

نشانه های برابری مثلث های قائم الزاویه.

دو مستطیل شکلاگر یکی از شرایط زیر وجود داشته باشد مثلث ها مساوی هستند:

1) پاهای آنها برابر است.

2) ساق و هیپوتنوز یک مثلث با ساق و هیپوتنوز دیگری برابر است.

3) هيپوتنوز و زاويه حاد يك مثلث با زاويه هيپوتنوز و حاد ديگري برابر است.

4) ساق و زاویه حاد مجاور یک مثلث با ساق و زاویه حاد مجاور دیگری برابر است.

5) ساق و زاویه حاد مقابل یک مثلث برابر با ساق و زاویه حاد مخالف دیگری.

خطوط و نقاط شگفت انگیز در مثلث.

ارتفاع مثلث استعمود،از هر راس به طرف مقابل پایین می آید ( یا ادامه آن). این طرف نامیده می شودپایه مثلث . سه ارتفاع یک مثلث همیشه همدیگر را قطع می کننددر یک نقطه، تماس گرفت اورتوسنترمثلث. مرکز یک مثلث حاد (نقطه O ، شکل 26) در داخل مثلث قرار دارد ومرکز متعامد یک مثلث منفرد (نقطه O ، شکل 27) – خارج از؛ مرکز قائم مثلث قائم الزاویه با راس زاویه قائم الزاویه منطبق است.

میانه - این بخش خط ، هر راس مثلث را به وسط ضلع مقابل متصل می کند. سه وسط یک مثلث (AD, BE, CF, Fig.28) در یک نقطه تلاقی می کنند O ، همیشه در داخل مثلث دراز کشیده استو او بودن مرکز گرانش. این نقطه هر میانه را به نسبت 2:1 تقسیم می کند و از رأس شمارش می کند.

نیمساز - این بخش نیمساززاویه از راس به نقطه تقاطع با طرف مقابل سه نیمساز یک مثلث (AD, BE, CF, Fig.29) در یک نقطه تلاقی می کنند اوه، همیشه در داخل مثلث دراز کشیدهو بودن مرکز دایره محاط(به بخش «درج شده مراجعه کنیدو چند ضلعی های محدود شده").

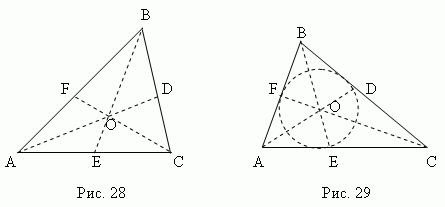
نیمساز طرف مقابل را به قطعاتی متناسب با اضلاع مجاور تقسیم می کند ; به عنوان مثال، در شکل 29 AE: CE = AB: BC.

عمود بر میانه عمودی است که از وسط کشیده شده استنقاط قطعه (اضلاع). سه عمود بر مثلث ABC(KO، MO، NO، شکل 30 ) در یک نقطه O تقاطع می کنند که این است مرکز دایره محدود شده (نقاط K، M، N - نقاط وسط اضلاع مثلث ABC).

در یک مثلث حاد، این نقطه در داخل مثلث قرار دارد. در مبهم - خارج؛ در یک مستطیل - در وسط هیپوتانوز. مرکز ثقل، مرکز ثقل، مرکز و دایره محاطی فقط در یک مثلث متساوی الاضلاع منطبق هستند.

قضیه فیثاغورس. در مثلث قائم الزاویه، مربع طولهیپوتانوس برابر است با مجموع مجذورات طول پاها.

اثبات قضیه فیثاغورث به وضوح از شکل 31 نتیجه می گیرد. یک مثلث قائم الزاویه را در نظر بگیرید ABC با پاها الف، بو هیپوتانوز ج.

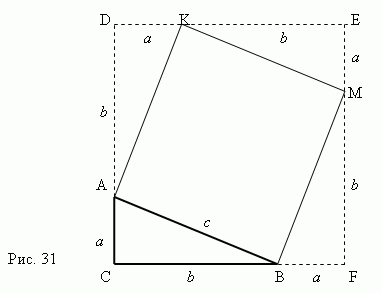
بیایید یک مربع بسازیم AKMB با استفاده از هیپوتانوز AB به عنوان یک طرف سپساضلاع مثلث قائم الزاویه را ادامه دهید ABC به طوری که یک مربع به دست آید CDEF ، که طرف آن برابر استa + b .اکنون مشخص است که مساحت میدان CDEF برابر است با ( a+b) 2 . از طرفی این مساحت برابر با مجموع استمناطق چهار مثلث قائم الزاویهو مربع AKMB یعنی

ج 2 + 4 (ab / 2) = ج 2 + 2 اب،

از اینجا،

ج 2 + 2 ab= (a+b) 2 ,

و در نهایت داریم:

ج 2 =آ 2 +b 2 .

نسبت ابعاد در یک مثلث دلخواه.

در حالت کلی (برای یک مثلث دلخواه) داریم:

ج 2 =آ 2 +b 2 – 2ab· cos ج

جایی که سی - زاویه بین اضلاعآو ب .