درس عملی "محاسبه مشتقات". درس عملی «محاسبه مشتقات» مشتق تابع y را بیابید
اهداف درس:
آموزشی- فرمول های تمایز را بدانید قوانین تمایز؛
تمایز یک تابع پیچیده؛ معنای فیزیکی و هندسی مشتق;
معادله مماس بر نمودار یک تابع.
رشدی -بتواند مشتقات توابع را پیدا کند. حل مسائل با استفاده از معنای فیزیکی، معنای هندسی؛ مقدار مشتق یک تابع را در یک نقطه پیدا کنید. به طور ریاضی اقدامات انجام شده را به درستی توضیح داده و توجیه کنید.
آموزشی –استقلال، مسئولیت پذیری، تفکر را پرورش دهید.
در طول کلاس ها
I. لحظه سازمانی.
II. بررسی تکالیف
(در زمان استراحت، مشاوران (دانش آموزان) را بررسی می کنند و نمرات را تعیین می کنند).
III. هدف گذاری و انگیزه
معلم به دانش آموزان اطلاع می دهد که این درس آخرین درس با موضوع "محاسبه مشتقات" است و از آنها دعوت می کند تا اهداف خود را تدوین کنند.
معلم: "فیلسوف بزرگ کنفوسیوس یک بار گفت: "سه راه به دانش منتهی می شود: راه تفکر اصیل ترین راه است، مسیر تقلید آسان ترین راه است و مسیر تجربه تلخ ترین راه است." بنابراین امروز در کلاس، هر یک از شما تعیین می کند که در کدام مسیر دانش این موضوع قرار دارد.
دانش آموزان وظیفه دارند دانش و مهارت های خود را در محاسبه مشتقات نشان دهند و به آنها یک طرح درسی داده می شود.
مرحله اول:با استفاده از کارت "به خاطر بسپار" کار را تکمیل کنید.
(آزمایش دانش فرمول ها و قواعد تمایز).
مرحله دوم:کار پیشانی شفاهی در مورد تکرار و تعمیم دانش.
مرحله سوم:"پیش بینی تست" (در هنگام انجام این کار، کمک مشاوران قابل قبول است).
منمرحله پنجم:حل یک مشکل عملی
مرحله پنجم:کار مستقل
مراحل I، III، V کار و تکالیف ارزیابی می شود. مشاوران نتایج را بررسی کرده و در جدول ارزیابی وارد می کنند.
معیارهای ارزیابی: "5"- 19-20 امتیاز؛
"4"- 15-18 امتیاز؛
"3"- 10-14 امتیاز.
راه های رسیدن به دانش
- بازتولید و تصحیح دانش مرجع
مرحله I.
هدف:کنترل، خودکنترلی دانش فرمول ها و قواعد تمایز
یاد آوردن! F.I. _________________________________________________ |
|
مشتق |
|
ج، ج - منفی تی |
|
|
|
|
|
f"(x)+ g"(ایکس) |
|
f(ایکس)* g(ایکس) |
|
|
|
در پایان این کار، یک خودآزمایی با استفاده از "جدول مشتقات" انجام می شود. کارت ها برای تایید به مشاوران تحویل داده می شوند (اصلاحات روی کارت ها مجاز نمی باشد).
V. تعمیم و نظام مند شدن دانش
مرحله دوم.
1. کار فرونتال دهان.
آ.برای این شرایط یک کار ایجاد کنید و آن را حل کنید.
![]()
1. مقدار مشتق تابع را در نقطه t = 3 بیابید. (پاسخ: 21.)
2. معادله ای برای مماس بر نمودار تابع در نقطه t = 3 ایجاد کنید. (پاسخ: y = 21x-45.).
3. اگر قانون حرکت با فرمول داده شود، سرعت جسم و شتاب را در لحظه t=3c بیابید. (پاسخ: 21 متر بر ثانیه، 16 متر بر ثانیه).
4. ضریب زاویه ای مماس رسم شده بر نمودار تابع را در نقطه t = 3 بیابید. (پاسخ: 21.).
5. مماس زاویه میل مماس بر نمودار تابع را در نقطه t = 3 بیابید و نوع زاویه بین مماس و جهت مثبت محور Ox را تعیین کنید. (پاسخ: tgα، زاویه α حاد است)
ب. مشتقات توابع را بیابید

2. مرحله III"پیش بینی تست"


در پایان این کار، خودآزمایی بر اساس پاسخ های نهایی انجام می شود و آزمون ها به مشاوران واگذار می شود. (اصلاحات روی کارت ها مجاز نیست).
پاسخ ها:
1 گزینه |
||||
گزینه 2 |
- راه حل مشکل
منمرحله V
راه حل جلویی برای یک مشکل سطح پیشرفته (راه حل توسط مشاوران همراه با کلاس انجام می شود).
وظیفه
در چه مقادیر پارامتری آمماس بر نمودار یک تابع ![]()
که در نقاط تقاطع آن با محور X رسم می شود، بین خود زاویه 60 درجه تشکیل می دهند؟

نمودار یک سهمی است با شاخه های رو به بالا که محور X را در دو نقطه قطع می کنند (مورد آ= 0 معنای مسئله را برآورده نمی کند):
IX جمع بندی و درجه بندی
1. سؤالات: الف) آیا هدف از درس محقق شده است؟
ب) کدام مرحله سخت ترین به نظر می رسید؟
ج) جالب ترین کدام بود؟
2. مشاوران نتایج (تعداد و اسامی دانشجویان در راه) را اعلام می کنند
تقلید، راه های تأمل و شیوه های تجربه).
کار عملی
ریاضیات
1. یافتن حد یک تابع. اولی و دومی محدودیت های شگفت انگیزی هستند.
2. مشتق تابع مختلط. مطالعه تابع یک متغیر و رسم نمودارها.
3. تست "کاربرد حساب دیفرانسیل در مطالعه توابع".
4. یافتن انتگرال های نامعین. محاسبه انتگرال های معین
5. محاسبه عوامل تعیین کننده.
6. حل سیستم معادلات خطی با استفاده از روش کرامر. تست.
7. حل مسائل در موضوع "مجموعه ها". فرمول های جبر منطقی
8. محاسبه احتمالات رویدادهای تصادفی. فرمول احتمال کل
9. محاسبه مشخصات عددی.
10. تست "مبانی نظریه احتمالات و آمار ریاضی"
11. شکل مثلثاتی یک عدد مختلط.
12. اعمال با اعداد مختلط به اشکال مختلف.
دستورالعملهای روششناسی برای کار عملی در ریاضیات
دوره 2
درس عملی شکلی از سازماندهی فرآیند آموزشی است که شامل انجام یک یا چند کار عملی توسط دانش آموزان بر اساس تکلیف و با راهنمایی معلم می شود.
بنابراین در کلاس های عملی ریاضی، دانش آموزان توانایی حل مسائل را پرورش می دهند که در آینده باید از آن برای حل مسائل حرفه ای در رشته های خاص استفاده کرد.
در دوره کار عملی، دانش آموزان بر توانایی استفاده از منابع اطلاعاتی، کار با اسناد نظارتی و مواد آموزشی، کتاب های مرجع، ساختن نقشه ها، نمودارها، جداول، حل انواع مسائل و انجام محاسبات مسلط می شوند.
مسائلی که در درس های عملی ریاضی حل می شوند:
1) گسترش و تثبیت دانش نظری در ریاضیات به دست آمده در طول سخنرانی.
2) توسعه مهارت ها و توانایی های عملی لازم برای حل موفقیت آمیز مسائل در ریاضیات در دانش آموزان.
3) رشد نیاز دانش آموزان به خودآموزی و ارتقای دانش و مهارت در فرآیند مطالعه ریاضی.
4) شکل گیری نگرش خلاق و رویکرد پژوهشی در فرآیند مطالعه ریاضی.
5) شکل گیری ویژگی های حرفه ای قابل توجه یک متخصص آینده و مهارت های به کارگیری دانش کسب شده در زمینه حرفه ای.
درس عملی شماره 1.محاسبه حدود تابع اولی و دومی محدودیت های شگفت انگیزی هستند.
موضوع : محاسبه حدود تابع
هدف: کسب دانش پایه در زمینه شاخه های بنیادی ریاضیات . آزمایش جذب دانش در محاسبه حدود توابع. دانش را در مورد این موضوع تکرار و سیستماتیک کنید.
وظایف:
توسعه تفکر حرفه ای خلاق؛
تسلط بر زبان علم، مهارت در مفاهیم عملیاتی؛
تسلط بر مهارت های تنظیم و حل مسائل؛
تعمیق آموزش نظری و عملی؛
توسعه ابتکار و استقلال دانش آموزان.
تقویت مهارت های محاسباتی؛
به کار بر روی گفتار ریاضی ادامه دهید.
شکل گیری مهارت های کار مستقل، کار با کتاب درسی، مهارت های کسب مستقل دانش؛
توسعه توانایی برجسته کردن چیز اصلی هنگام کار با متن.
شکل گیری تفکر مستقل، عملیات ذهنی: مقایسه، تجزیه و تحلیل، سنتز، تعمیم، قیاس.
نقش کار سیستماتیک برای تعمیق و افزایش قدرت دانش، در فرهنگ تکمیل وظایف را به دانش آموزان نشان دهید.
رشد توانایی های خلاقانه دانش آموزان.
ارائه کار عملی:
مطالب نظری توصیه های روش شناختی برای کار عملی.
ریاضیات، – سری: آموزش متوسطه حرفه ای. - روستوف روی دان "ققنوس"، ص.
پیشرفت درس عملی.
1.تدوین موضوع درس، تبیین ارتباط موضوع با سایر موضوعات رشته تحصیلی.
2. بررسی آمادگی دانش آموزان برای کلاس.
3. اجرای درس واقعی با توجه به موضوع و مطابق با برنامه کاری رشته:
مطالب نظری را با موضوع "محاسبه حدود توابع" مطالعه کنید.
نمونه هایی از حل وظایف معمولی را در نظر بگیرید.
کار مستقلی را روی محاسبه حدود توابع با استفاده از حد قابل توجه اول و دوم انجام دهید.
به سوالات امنیتی جواب بدهید.
اطلاعات نظری و توصیه های روش شناختی
در مورد حل مسئله
1. ارائه مطالب نظری.
برای محاسبه حد یک تابع در یک نقطه، باید:
1) به جای متغیر x چیزی که x تمایل دارد جایگزین کنید.
2) اگر پس از تکمیل مرحله 1) فرم عدم قطعیت را دریافت کردیم https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">و جایگزین کنید فلش با منهای: (x-a).
3) اگر پس از تکمیل مرحله 1، فرم عدم قطعیت دریافت کردیم https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> در ارتباط با مقادیر توابع مثلثاتی، باید از اولین حد قابل توجه استفاده کنیم.
تعریف.اولین حد قابل توجه حد نامیده می شود
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) تعریف:دومین محدودیت قابل توجهحد نامیده می شود

عدد داده شده توسط این حد نقش بسیار مهمی هم در آنالیز ریاضی و هم در شاخه های دیگر ریاضیات دارد. شماره تماس گرفته می شود پایه لگاریتم های طبیعی ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. تلفیق مطالب مورد مطالعه.
مثال 1
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
از قانون 1) استفاده کردیم و به جای x چیزی را که x باید برای آن تلاش کند، یعنی x=2 جایگزین کردیم.
مثال 2
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
مثال 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6
مثال 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" height="30 src=">
مثال 5
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
مثال 6
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
ب) 
V) 
3. تلفیق دانش، مهارت ها و توانایی ها.
کار مستقلی را روی محاسبه حدود توابع انجام دهید.
کار عملی شماره 1. انتخاب 1 حد تابع را محاسبه کنید: 1. 2. 3. 10. | کار عملی شماره 1. گزینه 2 حد تابع را محاسبه کنید: 1. 2. 3. 10. |
کار عملی شماره 2.
موضوع : یافتن مشتق تابع. مطالعه تابع یک متغیر و رسم نمودار.
هدف : آزمون عملی دانش مفهوم مشتق تابع، توانایی یافتن مشتقات توابع ابتدایی، توابع مختلط، توابع معکوس، با استفاده از جدول مشتقات و قوانین تمایز، مفهوم تابع مختلط و معکوس، توانایی استفاده از مشتق برای مطالعه توابع
ارائه کار عملی:
کتاب درسی. "ریاضیات". - M.: Bustard، 2010.
ریاضیات. M: Forum-Infa 2008.
کارت های فردی با گزینه کار عملی.
1. مطالب نظری و مثال های یافتن مشتق تابع.
تعریف:مشتق تابع f(x) (f"(x)) در نقطه x حد نسبت افزایش تابع به افزایش آرگومان است زمانی که افزایش آرگومان به صفر میل می کند:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
قوانین تمایز.
اگر توابع f(x) و g(x) مشتقاتی داشته باشند، پس
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′، که در آن C=const
5..png" width="49" height="54 src=">
6. مشتق تابع مختلط:
f′(g(x))=f′(g) g′(x)
2. مثال ها.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).
این تابع حاصل دو عامل است: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
تابع ضریب دو عبارت است: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " height="57 src=">.png" width="197 height=36" height="36">
راه حل. بیایید مشتق این تابع را با استفاده از قانون تمایز توابع پیچیده پیدا کنیم (فرمول 6):

5. اگر، پس 
6. y = ایکس 3 – 3ایکس 2 + 5ایکس+ 2. بیایید پیدا کنیم y "(–1).
y " = 3ایکس 2 – 6ایکس+ 5. بنابراین، y "(–1) = 14.
7. اگر y= ورود ایکس cos ایکس، آن y" = (ln ایکس)"cos ایکس+ln ایکس(cos ایکس) " =1/ایکس∙cos ایکس-لوگاریتم ایکسگناه ایکس.
اجازه دهید یک تابع داده شود. برای مطالعه آن نیاز دارید:
1) دامنه تعریف آن را بیابید. اگر خیلی سخت نیست، یافتن محدوده نیز مفید است. (اما، در بسیاری از موارد، سؤال یافتن به زمانی موکول میشود که مادونهای تابع پیدا شود.)
2) خصوصیات کلی تابع را که به تعیین رفتار آن کمک می کند بیابید: زوج یا فرد بودن تابع، تناوبی بودن آن.
3) در صورت وجود چنین نقاط مرزی، زمانی که آرگومان به نقاط مرزی حوزه تعریف نزدیک می شود، نحوه عملکرد تابع را پیدا کنید. اگر تابعی دارای نقاط ناپیوستگی باشد، این نقاط نیز باید از نظر وجود مجانب عمودی تابع بررسی شوند. مجانب مایل را پیدا کنید.
4) نقاط تقاطع نمودار را با محورهای مختصات بیابید که به سادگی از محاسبه مقدار تابع در شرایط زیر تشکیل شده است:
با محور OX: y=0;
با محور OY: x=0.
پیدا کردن نقاط تقاطع با محور ممکن است منجر به نیاز به حل یک معادله جبری پیچیده شود که شاید فقط به طور تقریبی قابل انجام باشد. با یافتن ریشه های تابع و نقاط ناپیوستگی، می توانیم علامت تابع را در هر یک از فواصل بین این نقاط تعیین کنیم. این کار را می توان با محاسبه مقدار تابع در هر نقطه از بازه یا با استفاده از روش فاصله انجام داد.
5) فواصل یکنواختی را بیابید. برای انجام این کار، مشتق را پیدا کنید و نابرابری را حل کنید:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">، عملکرد در حال کاهش است.
با یافتن فواصل یکنواختی، میتوانیم فوراً نقاط افراطی موضعی را تعیین کنیم: جایی که افزایش با کاهش جایگزین میشود، حداکثر محلی قرار میگیرد و جایی که کاهش با افزایش جایگزین میشود، حداقلهای محلی قرار میگیرند.
6) یافتن فواصل تحدب و تقعر با استفاده از مشتق دوم انجام می شود..png" width="39" height="19 src="> در فواصل:
اگر https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0، منحنی نمودار تابع محدب است.
در عین حال، نقاط عطف را به عنوان نقاطی تعریف می کنیم که در آن تابع جهت تحدب را تغییر می دهد (و پیوسته است).
7) یافتن نقاط تلاقی نمودار با مجانب و نقاط اضافی. این نکته اجباری نیست اما یافتن چنین نکاتی مطالعه تابع و نمودار آن را کامل و کامل می کند.
توجه داشته باشید که ترسیم فوراً نقاط روی محورهای مختصات و نموداری که در حین مطالعه توابع روی نقشه به دست می آیند مفید است. این به درک ظاهر نمودار در طول مسیر کمک می کند.
3. خودتان این کار را انجام دهید:
|
گزینه | مشتق تابع y را پیدا کنید: |
گزینه | مشتق تابع y را پیدا کنید: |
1.y=6- | 1. y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
درس عملی
موضوع:یافتن مشتقات کاربرد مشتق در مطالعه توابع و رسم نمودارها.
هدف: در محاسبه مشتقات مسلط شوید، یاد بگیرید که یک تابع را با استفاده از مشتق کشف کنید
وسایل آموزشی:نوت بوک برای تمرین های عملی، ارائه در مورد موضوع، منابع اینترنتی.
1. مطالب نظری را در مورد موضوعات: "قوانین محاسبه مشتقات"، "افراط تابع"، "تحدب، تقعر" در نظر بگیرید. نقطه عطف."
2. نمونه هایی از تکالیف را مرور کنید.
3. تکلیف تست شماره 1 را کامل کنید.
سوالات کنترلی:
1. حداکثر (حداقل) یک تابع را در یک نقطه تعریف کنید. در مورد علامت افزایش تابع در همسایگی نسبتاً کوچک حداکثر (حداقل) نقطه چه می توان گفت؟
2. شرایط لازم برای وجود یک تابع چیست؟ معنای هندسی آنها چیست؟
3. قاعده یافتن بزرگترین و کوچکترین مقادیر یک تابع در یک قطعه چیست؟
4. تحدب (تعرفه) یک منحنی را در یک بازه تعریف کنید.
5-قاعده یافتن فواصل تحدب و تقعر منحنی چیست؟
6. نقطه عطف منحنی. چگونه او را پیدا کنیم؟
7. الگوریتم ساخت نمودار یک تابع چیست؟
قوانین برای محاسبه مشتقات
مشتق تابع مختلط
اگر در=ƒ( و), u=φ(x)، سپس در¢ ( ایکس)=ƒ¢ (i)·φ¢ (ایکس).
مشتق از یک جمع.
اگر در(ایکس)=و(ایکس)+v (ایکس) آن در¢ (ایکس)=و¢ (ایکس)+v ¢ (ایکس)
مشتق محصول.
اگر y(x)=u(ایکس)· v (ایکس) آن در¢ = و¢ · v + تو · v ¢ .
به خصوص، ( با· و)¢ = ج· و¢، یعنی عامل ثابت از زیر علامت مشتق خارج می شود. تأیید آن آسان است
(تو 2 ) ¢ = 2 u·u ¢ ، (u 3 ) ¢ =3u 2 تو ¢ , … , (u n ) ¢ =n·u n–1 تو ¢ .
مشتق از ضریب.
اگر پس از آن  .
.
جدول مشتقات
1. (با)¢ =0
برای یک تابع پیچیده: اگر u=u(x)، این که:
2. (ایکس)¢ =1
3. (ایکس α )¢ = α · ایکسα-1، آ- هر عدد واقعی
 .
.
3. 
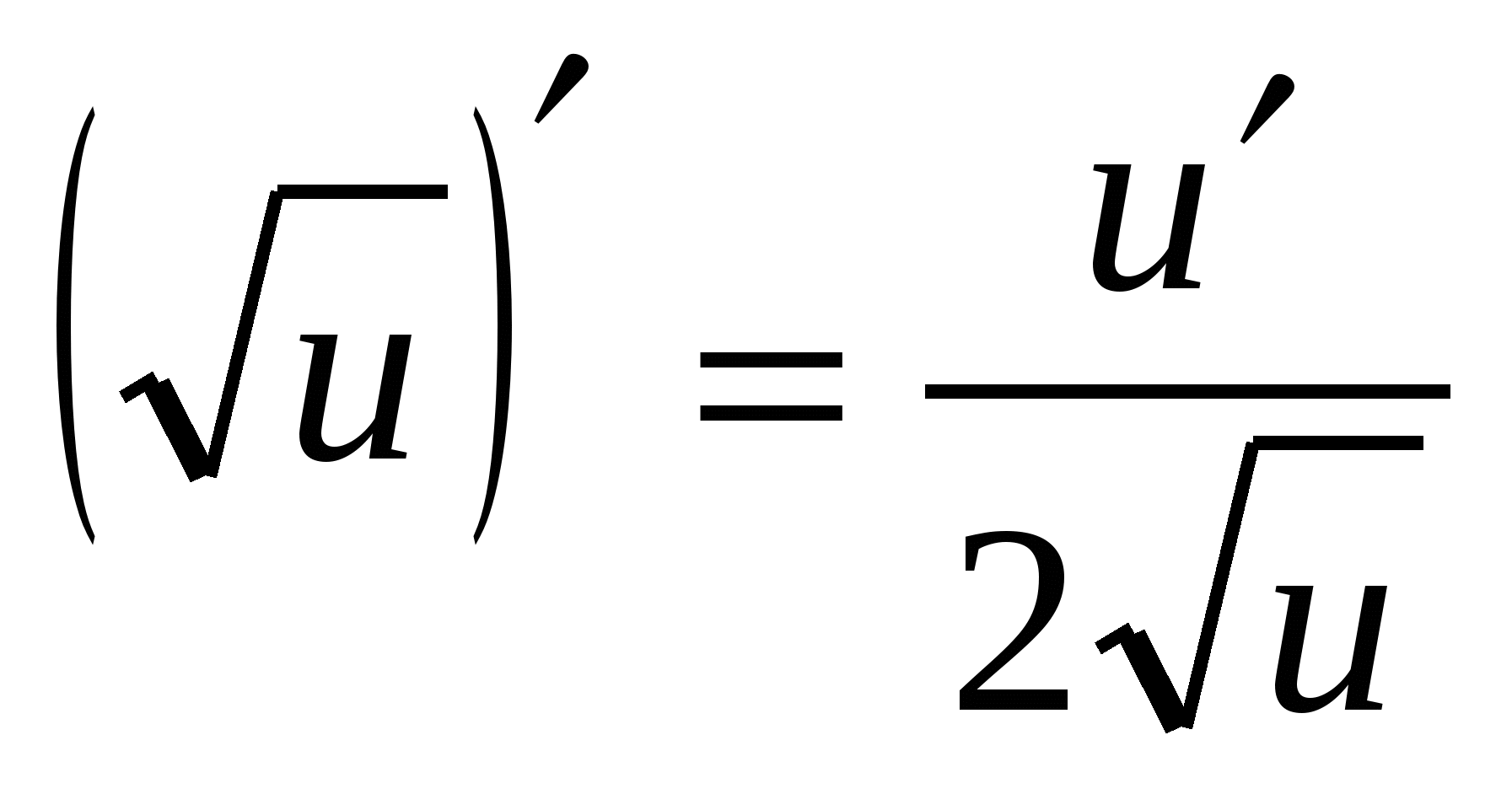
4. (آ ایکس ) ¢ =a ایکس · لوگاریتم آ
4. 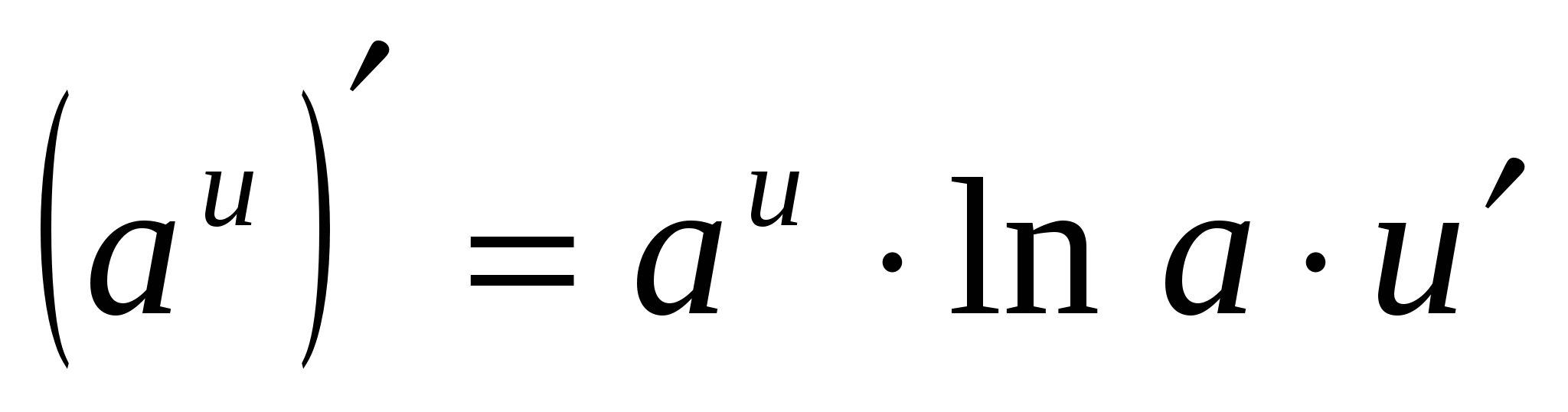
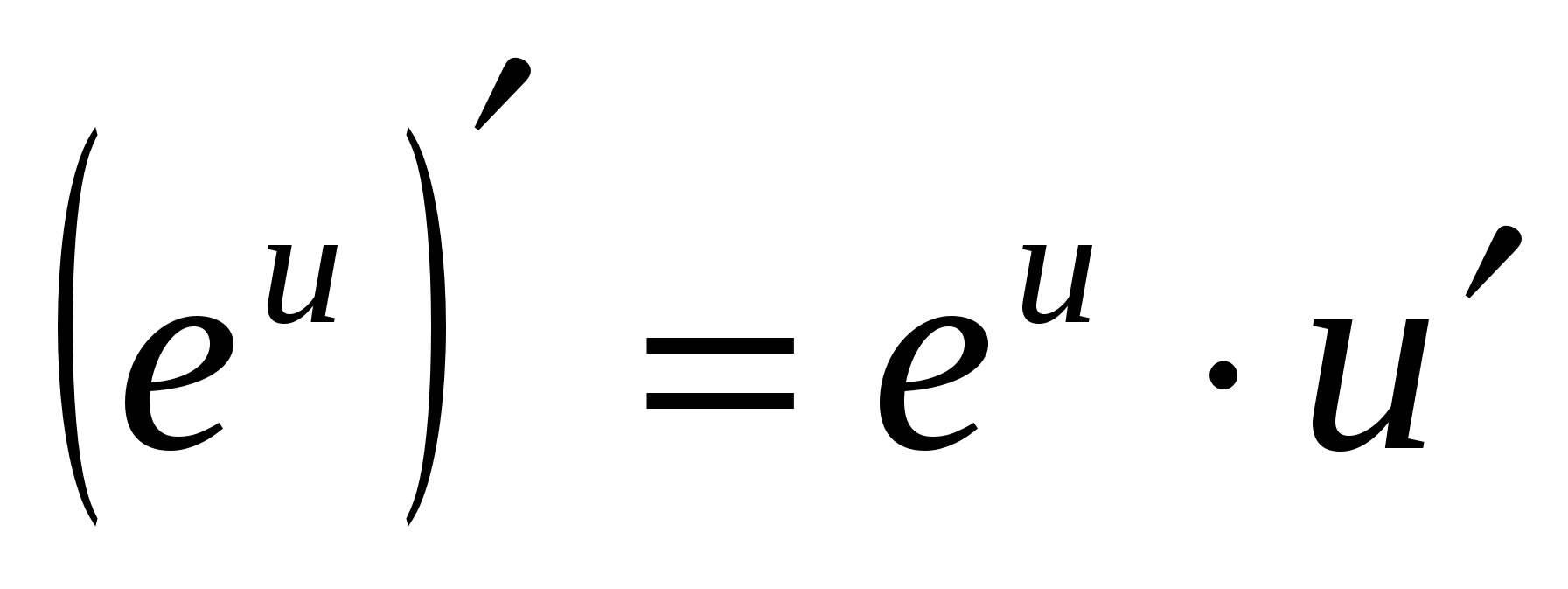
5. (ورود به سیستم
آ
ایکس)
¢
=
 .
.
5. 

6. (گناه x)¢ =cos x
6. 
7. (cos x)¢ = – sin x
7. 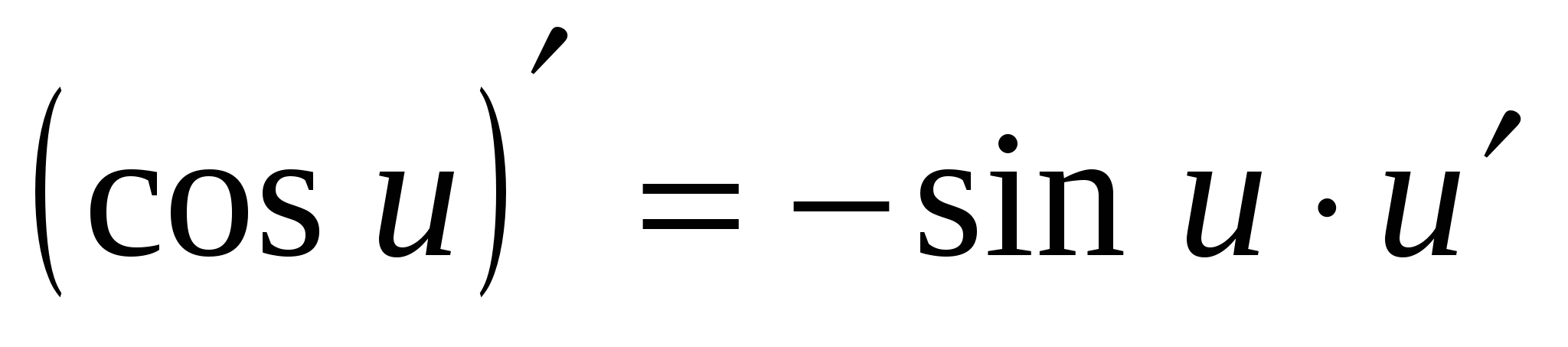
8. (tg x)¢
=
8. 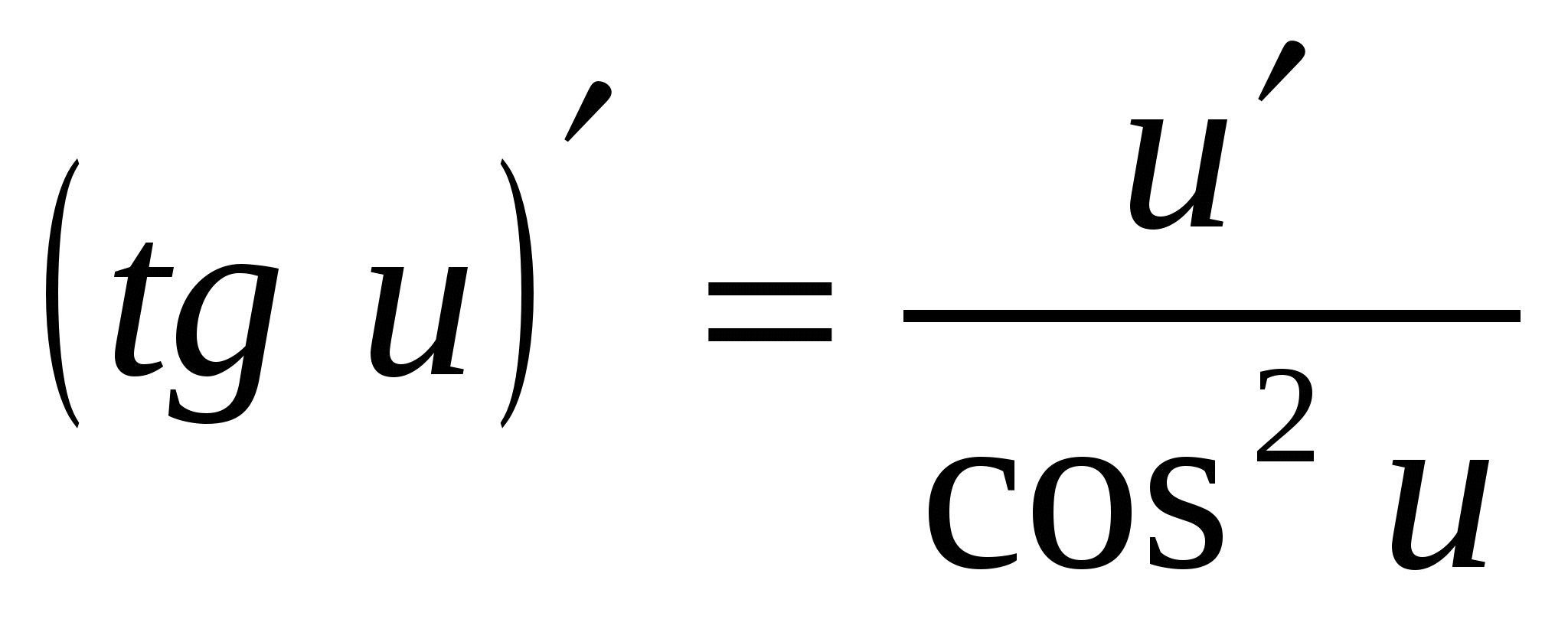
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 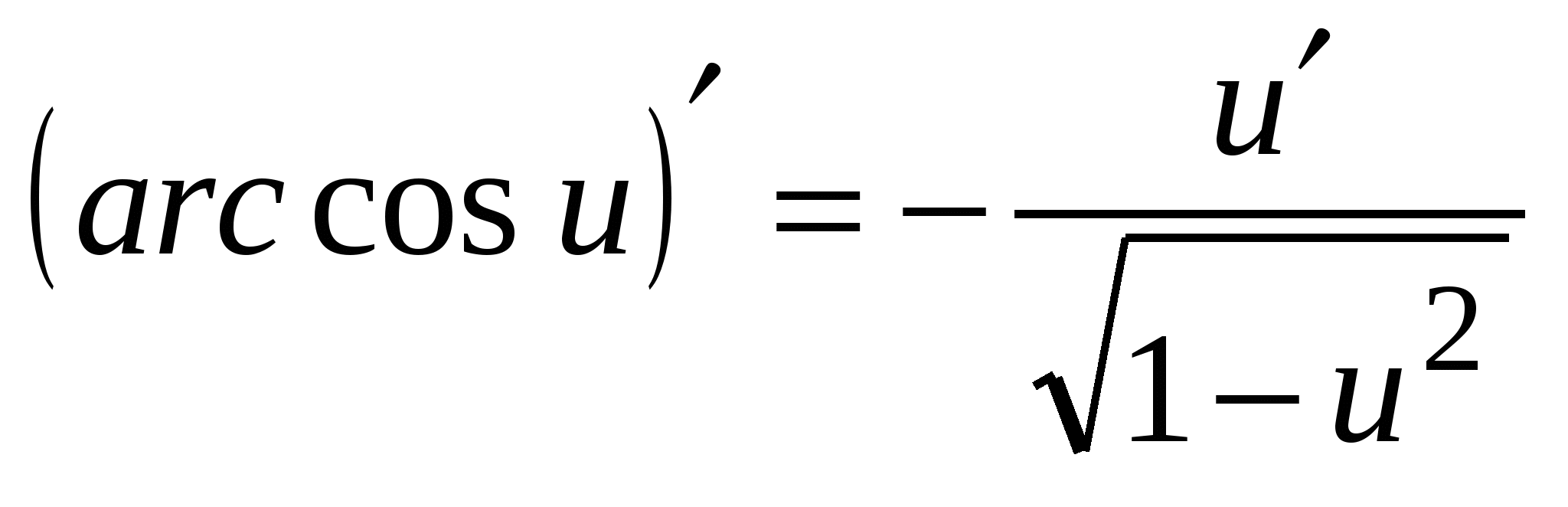
12. 
12. 
13. 
13. 
بررسی نمونه ها
مثال 1.
y=(3-2 گناه 5x ) 4 | ما فرمول های مشتق را برای و α ، گناه تو |
y ¢ =4·(3-2·sin5x) 3·(3-2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
مثال 2.
. 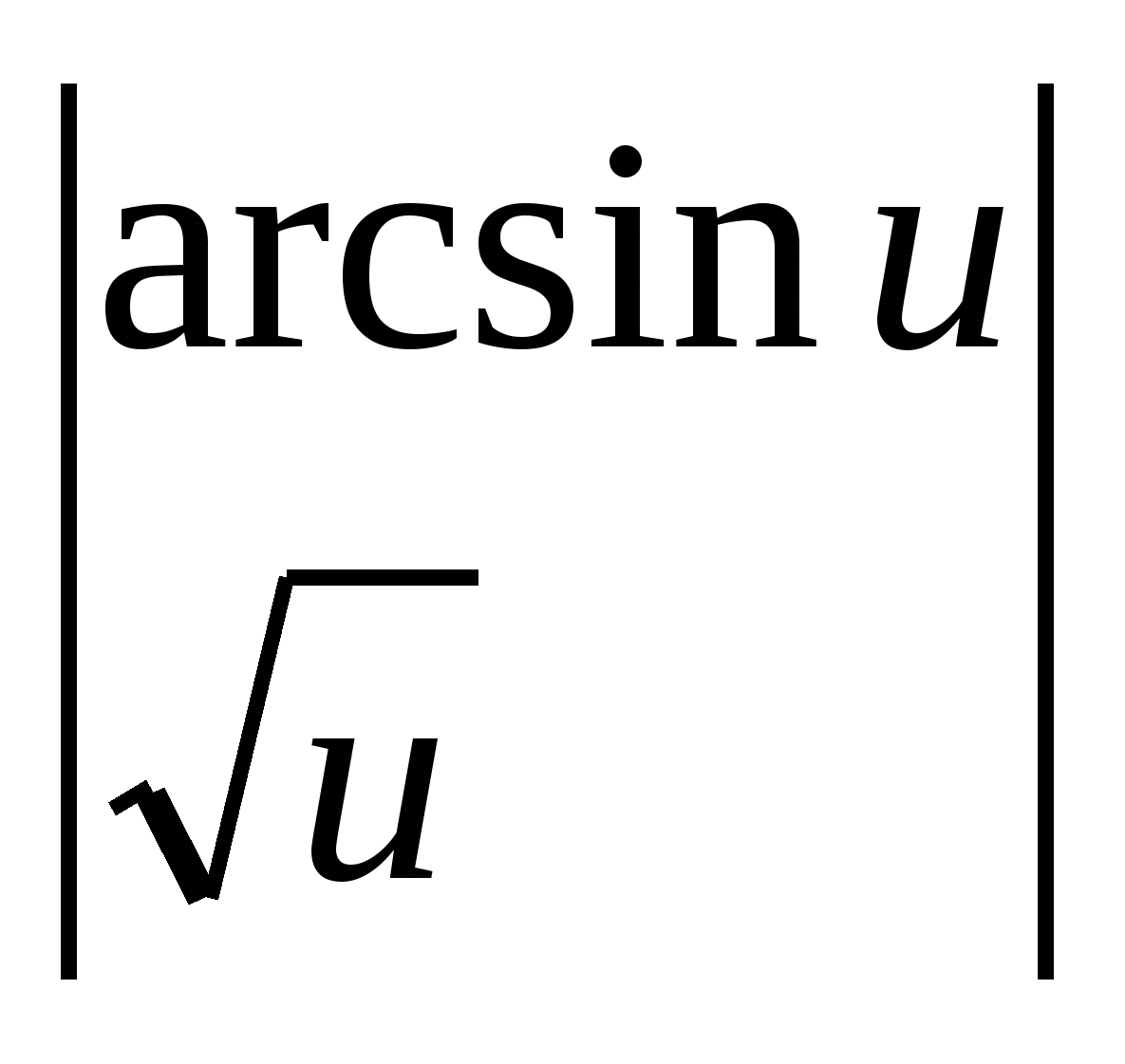

مثال 3.
 .
. 

مثال 4.



مثال 5.
 .
. 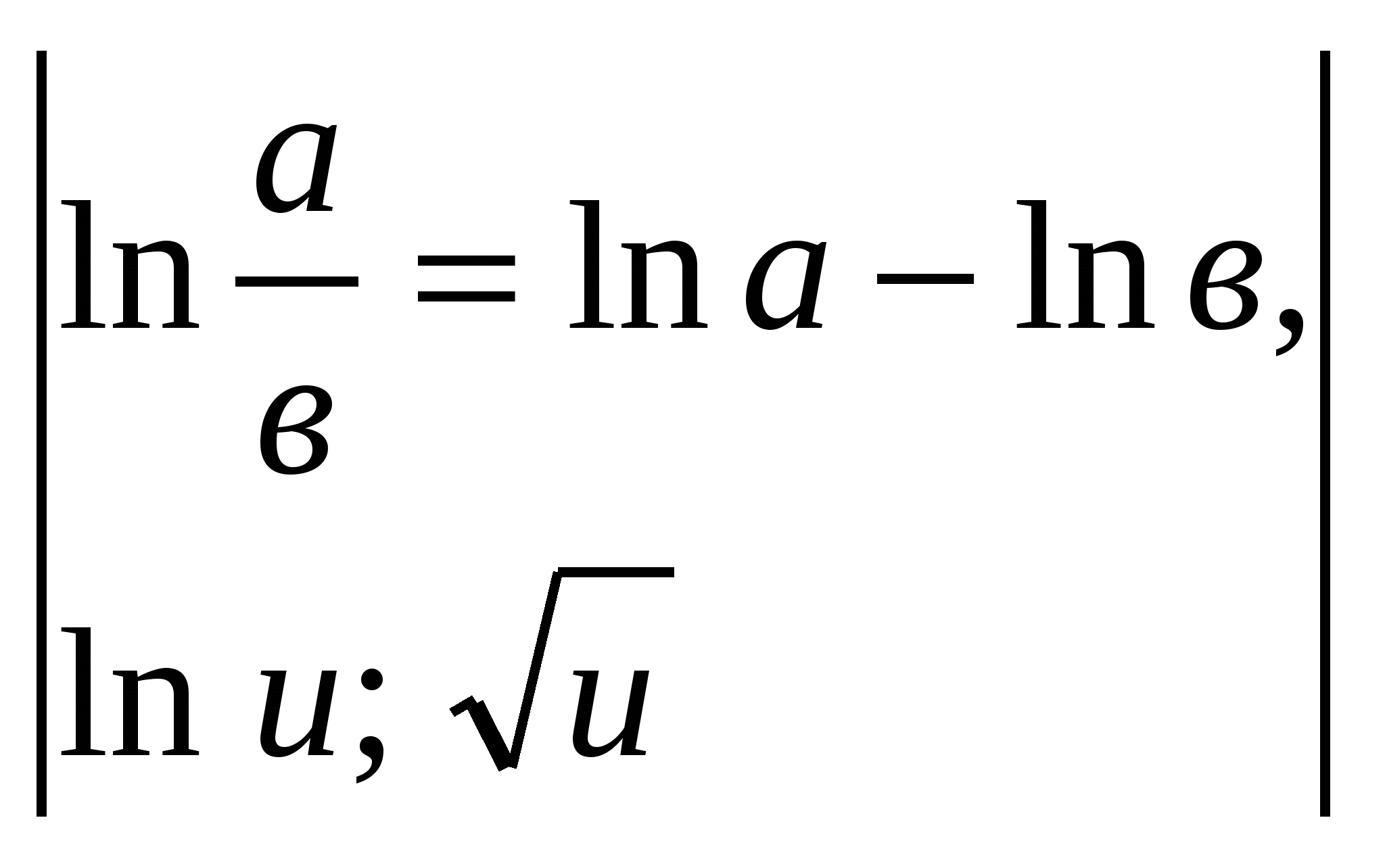

افراطی از عملکرد
مطالعه یک تابع در امتداد یکی از مهمترین کاربردهای مشتقات است. بیایید به تعریف حداقل و ماکزیمم و چگونگی پیدا کردن آنها نگاه کنیم.
اجازه دهید تابع ƒ( ایکس) بر روی یک مجموعه و یک نقطه مشخص و قابل تمایز است ایکس 0 یک نقطه در داخل آن است.
تعریف.تابع ƒ (ایکس) در نقطه ایکس 0 دارد بیشترین(حداقل)، اگر چنین همسایگی نقطه وجود داشته باشد ایکس 0 که برای همه است ایکساز این منطقه ƒ (ایکس) < ƒ (ایکس 0 ) (ƒ (ایکس) > ƒ (ایکس 0 )).
نقطه ایکسسپس 0 یک نقطه نامیده می شود بیشترین(کمترین).

برنج. 1.
نموداری از تابعی نشان داده شده است که دارای دو نقطه حداکثر ( ایکس 1 و ایکس 3) و دو حداقل امتیاز ( ایکس 2 و ایکس 4)، و حداکثر مقدار ممکن است کمتر از حداقل باشد ( ƒ (ایکس 1 ) < ƒ (ایکس 4)). این بر این واقعیت تأکید دارد که ما تکینگی یک تابع را فقط در نزدیکی یک نقطه مشخص مشخص می کنیم.
مقادیر تابع در نقاط ماکزیمم و کمینه را مقادیر افراطی یا افراط. نمودار بالا نشان می دهد که نقاط انتهایی ( ایکس 1 , ایکس 2 , ایکس 3 , ایکس 4) فواصل یکنواختی تابع را تعیین کنید که در هر یک از آنها مشتق علامت خاصی را حفظ می کند. البته در نقاط افراطی، مشتق به صفر می رسد. اجازه دهید یک قضیه در مورد آن فرمول بندی کنیم شرط لازم وجود یک افراط.
قضیه.اگر تابع ƒ (ایکس) در نقطه ایکس 0 یک انتها دارد، سپس مشتق تابع در این نقطه برابر با صفر است، یعنی ƒ¢ ( ایکس 0)=0.
بیایید بلافاصله توجه کنیم که این شرط کافی نیست، یعنی گزاره معکوس همیشه درست نیست. از برابری ƒ ¢ ( ایکس 0)= 0 لزوماً به این معنی نیست که در نقطه ایکس 0 یک افراط وجود دارد.
این با یک مثال با تابع تایید می شود ƒ (ایکس)=x 3 .
پیدا خواهیم کرد ƒ ¢ ( ایکس)= 3ایکس 2 . در نقطه ایکس=0 ƒ ¢ (0) = 0 . اما هر چقدر که دوست دارید به موضوع نزدیک شوید ایکس=0 پیدا خواهیم کرد ایکس> 0، کجا ƒ (ایکس)=x 3 > 0, ما پیدا خواهیم کرد ایکس< 0, где ¦ (ایکس)=ایکس 3 < 0. Т. е. не существует какая-либо малая окрестность точки ایکس= 0، جایی که برای همه ایکسمقدار تابع در یک نقطه ایکس=0 بزرگترین یا کوچکترین خواهد بود. بنابراین اشاره کنید ایکس=0 یک نقطه افراطی نیست.
می توان جور دیگری بحث کرد. از آنجایی که مشتق است ƒ ¢ (x)=3x 2 ، سپس تابع ƒ(x)=x 3 برای هر x واقعی افزایش مییابد و اکستریم ندارد.
نقاطی که در آن شرط اکستریم لازم برآورده می شود (ƒ ¢ (x)=0)نامیده می شوند بحرانی .
بدیهی است که مماس بر نمودار تابع در نقاطی که ƒ است ¢ (x)=0،موازی با محور x Ox .
شرایط کافیاکستریم در قضایای زیر آورده شده است.
قضیه 1.اگر ایکس 0 نقطه بحرانی تابع است و در هنگام عبور از آن مشتق تغییر علامت می دهد، سپس ایکس 0 یک نقطه افراطی است، یعنی اگر مشتق علامت مثبت به منفی را تغییر دهد، یک نقطه حداکثر و اگر علامت از منفی به مثبت تغییر کند، یک نقطه حداقل است.
توجه داشته باشید که اگر مشتق علامت تغییر نکند، در نقطه ای اکسترومی وجود ندارد. قاعده تحصیل اکستریم با استفاده از مشتق اول از درس مدرسه معلوم است. گاهی اوقات راحت تر است که یک شرط کافی برای یک اکستریم با استفاده از مشتق دوم تنظیم شود.
اجازه دهید تابع ƒ( ایکس) دو بار در برخی دامنه ها قابل تمایز است (یعنی ƒ( ایکس) دارای ƒ¢ ( ایکس) و ƒ ¢¢ ( ایکس)).
قضیه 2.اگر ایکس 0 - نقطه بحرانی تابع ƒ(x)و ƒ ¢¢ (ایکس 0 ) > 0 ، آن ایکس 0 - حداقل امتیاز، اگر ƒ ¢¢ (ایکس 0 ) < 0, то ایکس 0 - حداکثر امتیاز
با استفاده از مشتق دوم، تحدب یا تقعر نمودار یک تابع مشخص می شود.
تحدب، تقعر. نقطه عطف.
منحنی y=ƒ(ایکس) نامیده میشود محدبهفتم زیرهر کدام از او مماس
ƒ ¢¢ ( ایکس) < 0.
منحنی y=ƒ(ایکس) نامیده میشود مقعر در یک بازه زمانی که تمام نقاط منحنی قرار دارند بالاتر هر کدام از او مماس در این فاصله سپس در این فاصله
ƒ ¢¢ (x) > 0
تعریف. نقطه عطف منحنی نقطه ای است که در یک طرف آن منحنی محدب و از طرف دیگر مقعر است.
در نقطه عطف ƒ ¢¢ ( ایکس)=0.
بنابراین، علامت مشتق دوم (و همچنین علامت خود تابع و مشتق اول آن) ویژگی های نمودار تابع را نشان می دهد. بیایید دوباره به آنها نگاه کنیم.
اگر برای همه ایکسدر فاصله زمانی ( آ, ب) ƒ (ایکس) > 0 (ƒ (ایکس) < 0)، سپس نمودار در بالای (زیر) محور x قرار دارد.
اگر برای همه ایکسدر فاصله زمانی ( آ, ب) ƒ ¢ ( ایکس) > 0 (ƒ ¢ ( ایکس) < 0), то функция на (آ, ب) زیاد می شود (کاهش می یابد).
اگر برای همه ایکسدر فاصله زمانی ( آ, ب) ƒ ¢¢ ( ایکس) > 0 (ƒ ¢¢ ( ایکس) < 0), то график на (آ, ب) مقعر (محدب).
معادله ƒ( ایکس)=0 «صفرهای» تابع، یعنی نقاط تقاطع نمودار با محور Ox را تعریف می کند.
معادله ƒ ¢ ( ایکس)=0 نقاط بحرانی را تعریف می کند.
معادله ƒ ¢¢ ( ایکس)=0 نقاط عطف احتمالی را تعریف می کند.
طرح مطالعه تابع
برای مطالعه عملکرد ƒ (ایکس) و نقشه کشی y=ƒ(ایکس) باید پیدا شود:
1) دامنه تعریف تابع و نقطه تقاطع نمودار با محورهای مختصات.
2) فواصل یکنواختی;
3) نقاط افراطی و مقادیر تابع در این نقاط؛
4) فواصل تحدب و تقعر نمودار.
5) نقاط عطف نمودار.
6) تمام نقاط به دست آمده را در یک سیستم مختصات دکارتی بسازید (گاهی اوقات برای روشن شدن نمودار، نقاط اضافی به دست می آید) و خود نمودار.
کوچکترین و بزرگترین مقادیر یک تابع در یک بخش
هنگام حل برخی از مسائل روش بهینه سازی، مهم است که بتوانیم کوچکترین یا بزرگترین مقادیر یک تابع را در یک بخش خاص پیدا کنیم. تابع یا در نقاط بحرانی یا در انتهای بخش به این مقادیر می رسد.
طرح جستجوکوچکترین و بزرگترین مقادیر تابع ƒ (ایکس) در بخش [ آ, ب].
1. مشتق تابع را بیابید ƒ ¢ ( ایکس).
2. نقاط بحرانی را از معادله بیابید ƒ ¢ ( ایکس)=0.
3. آن نقاط بحرانی را که به این بخش تعلق دارند انتخاب کنید [ آ, ب] و مقدار تابع را پیدا کنید ƒ (ایکس) در هر نقطه از این قبیل.
4. محاسبه مقادیر تابع ƒ (ایکس) در انتهای بخش: ƒ( آ) و ƒ( ب).
5. از مقادیر تابع به دست آمده، بزرگترین (بزرگترین) و کوچکترین (کوچکترین) را انتخاب کنید.
مثال 2.
بزرگترین و کوچکترین مقادیر یک تابع را پیدا کنید ƒ(x)=ایکس 3 -9x 2 +24x–10در بخش
1. ƒ ¢ ( ایکس)= 3ایکس 2 – 9·2 ایکس 2 + 24.
2. ƒ ¢ ( ایکس)=0, 3(ایکس 2 –6ایکس+8)=0, ایکس 1 =2, ایکس 2 =4.
3. نقطه x 2 = 4 به بخش تعلق ندارد. بنابراین، مقدار تابع را فقط در نقطه محاسبه می کنیم ایکس 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. مقادیر تابع در انتهای بخش: ƒ(0)= –10، ƒ(3)=3 3 –9·3 2 +24·3–10، ƒ(3)=8.
5. مقادیر به دست آمده:
ƒ(2)=10، ƒ(0)= –10، ƒ(3)=8.
بالاترین مقدار 10 است و در نقطه به دست می آید ایکس=2. کوچکترین برابر 10- است و در نقطه به دست می آید ایکس=0.
مثال 3.
فواصل تحدب و تقعر و نقاط عطف منحنی را بیابید y=x+36ایکس 2 –2ایکس 3 –ایکس 4 .
دامنه تعریف این تابع مجموعه تمام اعداد حقیقی است، یعنی. ایکسЄ(–∞, +∞).
بیایید مشتق دوم را پیدا کنیم.
در¢ = 1+72 ایکس–6ایکس 2 –4ایکس 3 .
در¢¢ = 72-12 ایکس–12ایکس 2 = –12(ایکس 2 +ایکس–6).
از معادله در¢¢ =0 ما آبسیسا نقطه عطف را می گیریم:
–12(ایکس 2 +ایکس–6)=0 ایکس 1 = –3; ایکس 2 =2.
بیایید علامت را تعریف کنیم در¢¢ در فواصل
(–∞; –3), (–3; 2), (2, +∞).
ایکس
(–∞, –3)
(–3; 2)
(2; +∞)
در¢¢
شکل منحنی
محدب
عطف
مقعر
عطف
محدب
بیایید مختصات نقاط عطف را پیدا کنیم:
در(–3)=726; م 1 (-3؛ 726) - نقطه عطف
در(2)=114; م 2 (2؛ 114) - نقطه عطف.
در بازه (-3؛ 2) منحنی مقعر است. در فواصل (–∞؛ –3) و (2؛ +∞) – محدب.
نمونه تکالیف
وظیفه شماره 1.
نقاط شکست تابع را پیدا کنید و نمودار را رسم کنید

تابع ƒ (ایکس) برای همه واقعی تعریف شده است ایکسو در هر یک از بازه های مشخص شده پیوسته است: (–∞; –1)، [–1; 0]، (0، +∞). بیایید عملکرد را بررسی کنیم ƒ (ایکس) برای تداوم در نقاط ایکس= -1 و ایکس=0.
برای انجام این کار، در هر یک از این نقاط محدودیت های یک طرفه پیدا می کنیم.

از آنجایی که محدودیت های یک طرفه متفاوت است، پس ایکس = –1 – نقطه ناپیوستگی از نوع اول.
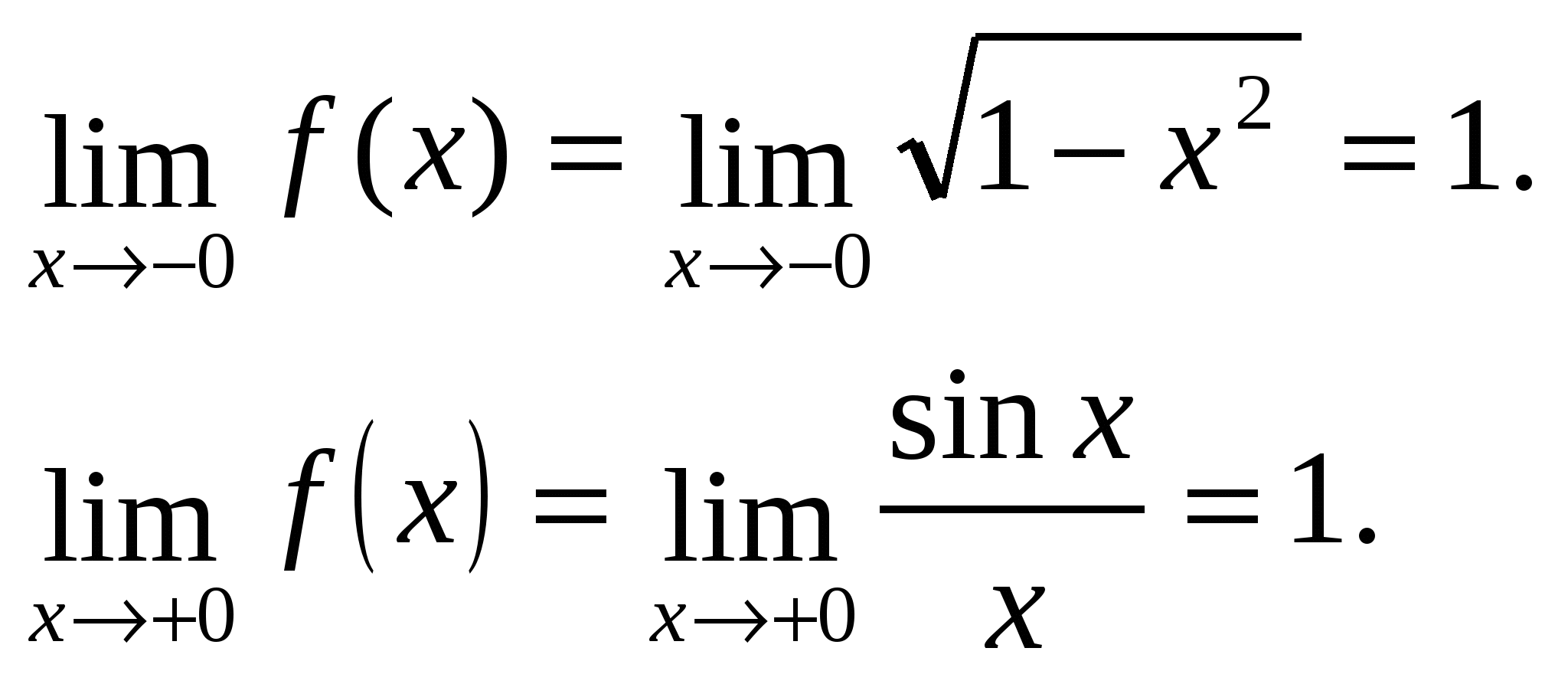
محدودیت های یک طرفه برابر هستند، یعنی در نقطه x=0 حدی از تابع و وجود دارد 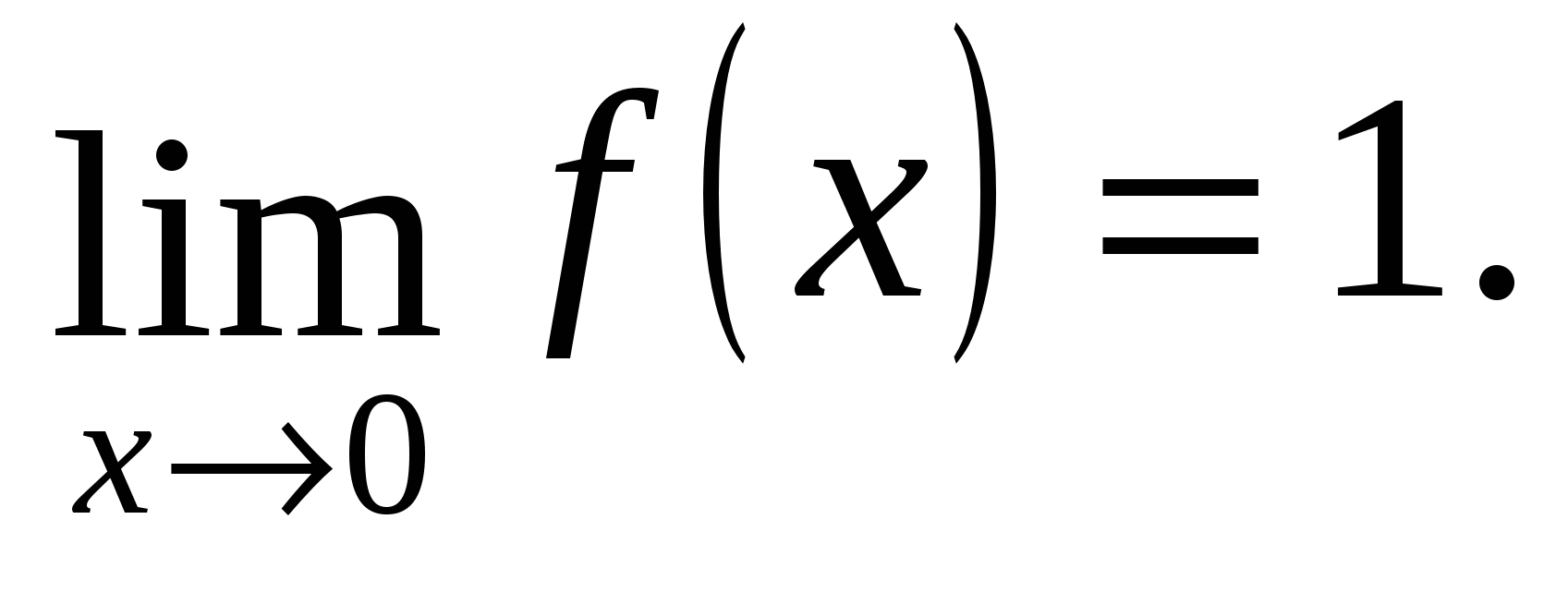
بیایید این حد را با مقدار تابع در نقطه مقایسه کنیم: 
زیرا  سپس در در x=0 تابع ƒ(x) پیوسته است.
سپس در در x=0 تابع ƒ(x) پیوسته است.
بیایید تابع ƒ را رسم کنیم (ایکس)، با توجه به اینکه
1)  - معادله یک خط مستقیم،
- معادله یک خط مستقیم،
2)  - معادله نیم دایره بالایی
- معادله نیم دایره بالایی  با مرکز در مبدا و شعاع برابر با وحدت، و در شرایط -1 £ ایکسمعادله 0 پوند
با مرکز در مبدا و شعاع برابر با وحدت، و در شرایط -1 £ ایکسمعادله 0 پوند  یک چهارم دایره را تعریف می کند.
یک چهارم دایره را تعریف می کند.
3) برای ایکس > 0 نمودار با معادله داده می شود  . نقاط تلاقی این منحنی را با محور Ox از معادله پیدا می کنیم
. نقاط تلاقی این منحنی را با محور Ox از معادله پیدا می کنیم 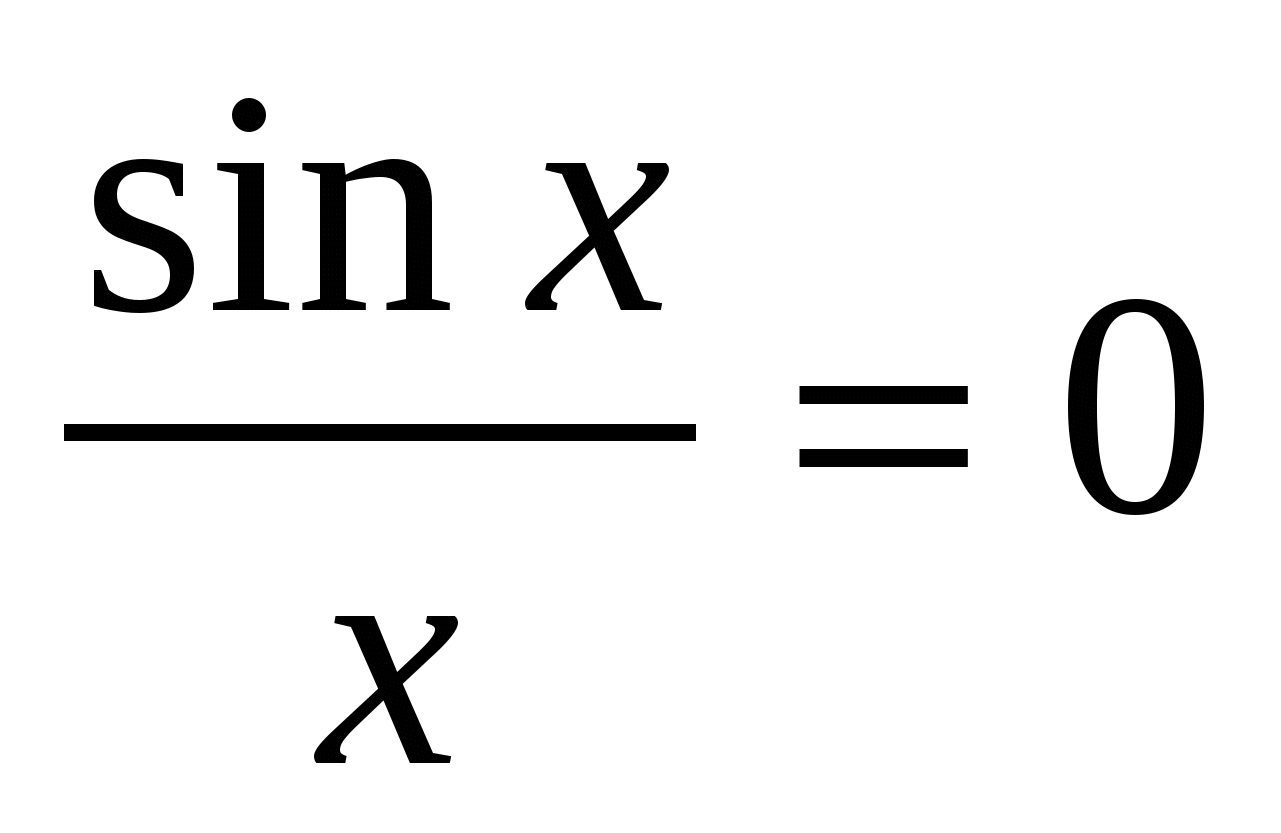 برای x > 0. x= π
n، جایی که n
=1, 2, 3, 4,
برای x > 0. x= π
n، جایی که n
=1, 2, 3, 4,

برنج. 2.
وظیفه شماره 2.
معادلات مماس بر یک خط را بنویسید  در نقاطی که ایکس=0 و ایکس=4. نقطه تلاقی مماس ها و زاویه بین آنها را پیدا کنید. یک نقاشی بکشید.
در نقاطی که ایکس=0 و ایکس=4. نقطه تلاقی مماس ها و زاویه بین آنها را پیدا کنید. یک نقاشی بکشید.
معادله مماس بر یک خط y=ƒ(x)به نظر می رسد
جایی که در 0 =ƒ( ایکس 0).
در نقطه ایکس=0 در(0)=ƒ(0)=5.
در¢ =ƒ ¢ (ایکس)=ایکس-3 ƒ¢ (0) = -3.
م 1 (0، 5) دارای فرم است y- 5= –3(ایکس-0) یا
y= –3ایکس+5.
در نقطه ایکس=4 در(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
معادله مماس در یک نقطه م 2 (4، 1) دارای فرم است y- 1=ایکس-4 یا
y=x–3.
نقطه تلاقی مماس ها را با حل سیستم بدست می آوریم

نقطه تقاطع م 3 (2, –1).
گوشه φ بین مماس ها از فرمول پیدا می کنیم:
 ,
,
جایی که ک 1 = –3; ک 2 = 1 - ضرایب زاویه ای مماس.
 .
.
گوشه φ =arctg 2.
بیایید این خط را بسازیم  - سهمی با راس در نقطه ای که ایکس= 3، زیرا در¢
= 0 در ایکس=3. پیدا خواهیم کرد
- سهمی با راس در نقطه ای که ایکس= 3، زیرا در¢
= 0 در ایکس=3. پیدا خواهیم کرد  . نقطه م 4 (3;
. نقطه م 4 (3;  ) رأس سهمی است.
) رأس سهمی است.
آر 
است. 3.
وظیفه شماره 3.
عملکرد کاوش 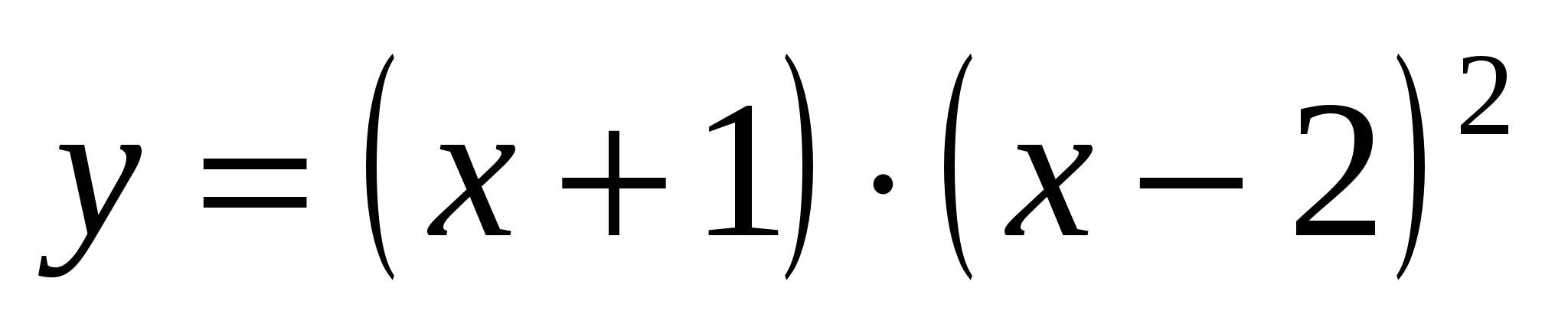 و آن را ترسیم کنید.
و آن را ترسیم کنید.
1. این تابع یک چند جمله ای است (شما می توانید براکت ها را باز کنید، ما یک چند جمله ای درجه سوم دریافت می کنیم)، بنابراین برای هر یک تعریف، پیوسته و قابل تمایز است. ایکس.
2. بیایید مشتق را پیدا کنیم.
 .
.
از معادله در¢ =0 بیایید نقاط بحرانی را پیدا کنیم: 3 ایکس·( ایکس–2)=0, ایکس 1 =0, ایکس 2 =2.
بیایید آنها را بررسی کنیم.
ایکس
(–∞, 0)
(0; 2)
(2; +∞)
در ¢
در
3. بنابراین، تابع در بازه های (–∞، 0) و (2، +∞) افزایش می یابد، در بازه (0؛ 2) کاهش می یابد، حداکثر در x=0 و حداقل در x=2 است:
در حداکثر = در(0)=4; دردقیقه = در(2)=0.
4. مشتق دوم را پیدا کنیم.
در¢¢ = 6·( ایکس-1).
منحنی در جایی که محدب است در¢¢ < 0, т. е. 6·(ایکس–1) < 0, ایکس < 1.
منحنی مقعر است که در آن در¢¢ > 0، یعنی ایکس > 1.
بنابراین، در بازه (–∞، 1) منحنی محدب است. و در بازه (1، +∞) مقعر است.
5. نقطه عطف را از معادله پیدا می کنیم در¢¢ =0. بدین ترتیب، ایکس=1 – آبسیسه نقطه عطف، زیرا این نقطه فواصل تحدب و تقعر منحنی را از هم جدا می کند. ترتیب نقطه عطف: در(1)=2.
نمودار یک تابع در=(ایکس+1)·( ایکس-2) 2 محور Ox را قطع می کند در=0، یعنی چه زمانی ایکس= -1 و ایکس=2;
از محور Oy در ایکس=0، یعنی چه زمانی در=4. ما سه امتیاز گرفتیم: (–1؛ 0)، (2؛ 0)، (0؛ 4). تمام امتیازهای به دست آمده را با اضافه کردن موارد مجاور به جدول وارد می کنیم.
–2
–1



–16


است. 4 منحنی y=(x+1)(x–2) 2.
وظیفه شماره 1
ما کارهایی را به شما معرفی می کنیم که ممکن است یک، دو، سه یا چند پاسخ صحیح داشته باشند. اعداد تمام پاسخ های صحیح را دایره بکشید.
1. اگر  سپس تابع
سپس تابع
1) افزایش
2) کاهش می یابد
3) ثابت
2. اگر
1) افزایش
2) کاهش می یابد
3. اگر  ، سپس تابع
، سپس تابع
1) افزایش
2) کاهش می یابد
4. اگر  ، سپس تابع
، سپس تابع
1) افزایش 3) کاهش
2) ثابت 4) یکنواخت
5. عملکرد  است
است
1) حتی
2) حتی نه
3) نه زوج و نه فرد
4) دوره ای
5) دوره ای نیست
6) مثلثاتی
7) ابتدایی
6. عملکرد  است
است
1) حتی
2) عجیب و غریب
3) نه زوج و نه فرد
4) دوره ای
5) دوره ای نیست
6) مثلثاتی
7) ابتدایی
2) وایرشتراس 4) دیریکله 6) لایب نیتس
8) راه حل  معادلات
معادلات
1) 0 3) 0 و 3 5) 2 7) 3
2) 2 و 3 4) 2 6) -5 و 1 8) 5 و 1
9) راه حل برای نابرابری 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 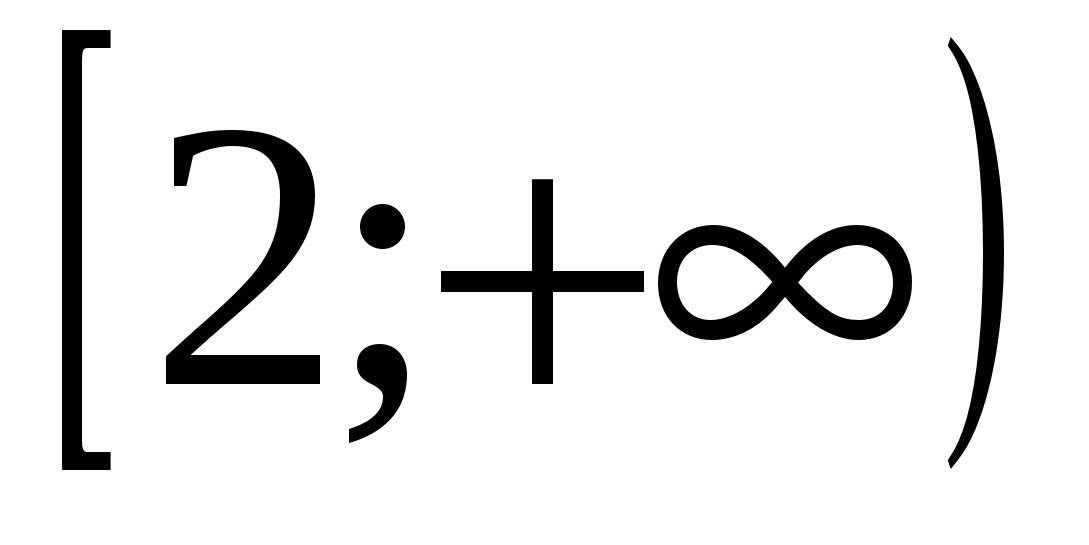
10) روش  مقدار پیدا می شود
مقدار پیدا می شود
1) بردارها
2) مستقیم
3) بخش
11) اگر  ، سپس تابع
، سپس تابع
1) مقعر 3) محدب 5) کاهشی
2) یکنواخت 4) افزایشی 6) ثابت
12) دامنه تعریف تابع برابر است با 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 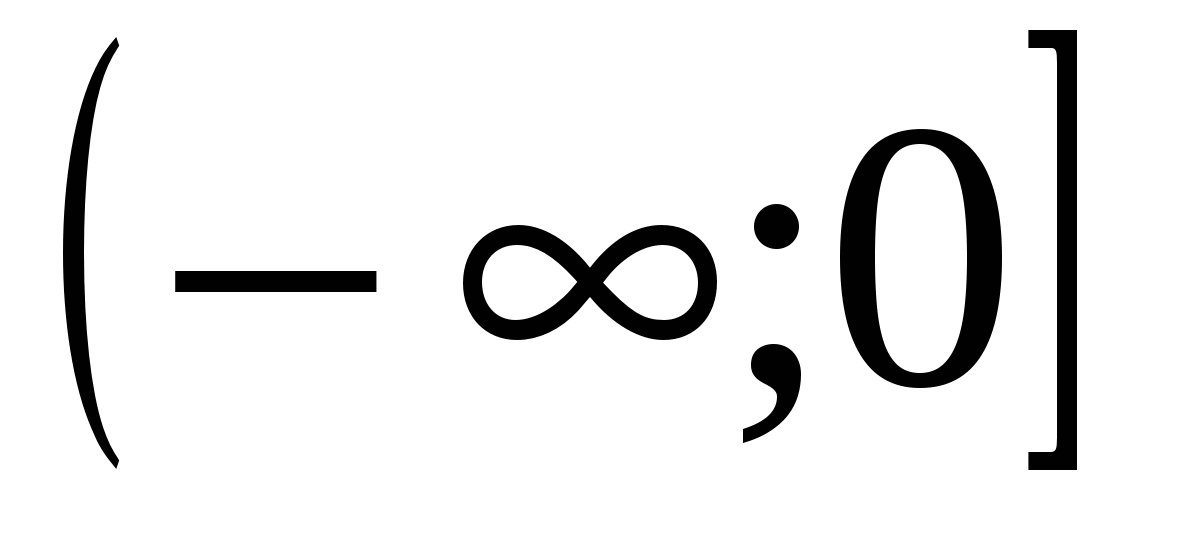
7) (-1;1)
8) 
9) 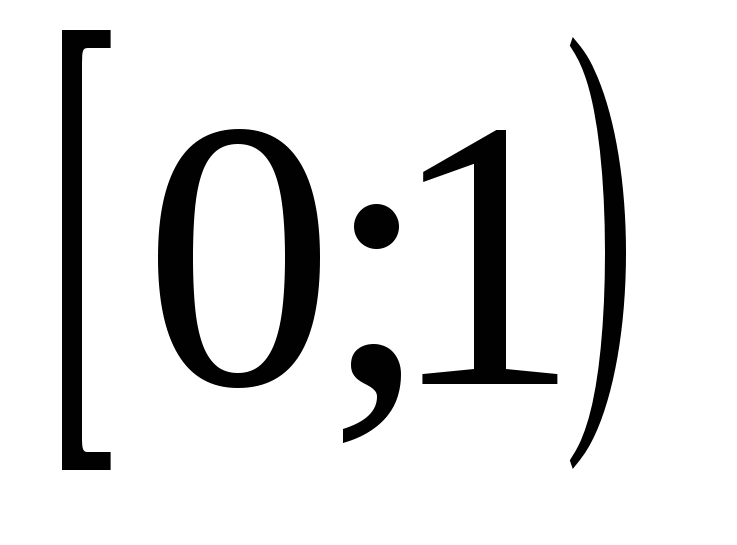
13) عملکرد  است
است
1) نشان دهنده
2) مثلثاتی
3) قدرت
4) لگاریتمی
14) اگر توابع y = ایکس  سپس او است
سپس او است 
1) حتی
2) عجیب و غریب
3) نه زوج و نه فرد
15) عملکرد  در
در  است
است

 .
.


