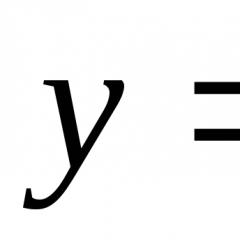آزمایش برای همگرایی انتگرال های نامناسب. چگونه یک انتگرال نامناسب را محاسبه کنیم و به همگرایی آن پی ببریم. تعریف و ویژگی های اساسی

قضیه 12.11 (آزمون مقایسه انتگرال های نامناسب). بگذارید توابع f(x) و g(x) در بازه [a, ">) پیوسته باشند و شرط 0 fix) ?(x) روی آن را برآورده کنند. سپس از همگرایی انتگرال

انتگرال همگرا می شود

و بالعکس، از واگرایی انتگرال (12.64) واگرایی انتگرال (12.63) می آید.

اثباتاجازه دهید نماد زیر را معرفی کنیم:

تابع P(K)بدون کاهش است؛ در واقع اگر و من 2، سپس

جی ثابت) dx>0 و سپس

بیایید دنباله ای از مقادیر (/?„) -> "> را در نظر بگیریم. سپس توالی مربوط به مقادیر تابع (F(Rn))یکنواخت و بدون کاهش است. بگذارید انتگرال (12.63) همگرا شود، سپس دنباله (67 ( آرآن)) محدود است. اما پس از آن توالی نیز محدود است (F(/?„))، یعنی با قضیه 7.13 همگرا می شود. بنابراین محدودیتی وجود دارد F(R)در آر-+ «>، یعنی. انتگرال (12.64) همگرا می شود.

حال اجازه دهید قسمت دوم قضیه را اثبات کنیم. اجازه دهید انتگرال (12.64) واگرا شود. اگر فرض کنیم که انتگرال (12.63) همگرا شود، با آنچه در بالا ثابت شد، انتگرال (12.64) نیز باید همگرا شود که با شرط در تضاد است. قضیه ثابت شده است. ?

اظهار نظر.یک معیار مقایسه مشابه برای انتگرال های نادرست نوع دوم نیز معتبر است. اگر توابع /(x) و g (ایکس)پیوسته در نیم فاصله [a>b)و برای همه نقاط در برخی از همسایگی نقطه مفرد بتکمیل شد

شرایط 0 (x)، سپس از همگرایی انتگرال Jg(x)dx نتیجه می شود که

واگرایی انتگرال J/(x)dx و از واگرایی انتگرال J/(x)dx -

توان انتگرال Jg(x)dx.

اجازه دهید مثال هایی را برای مطالعه همگرایی انتگرال های نامناسب در نظر بگیریم.

مثال 27. ت. ^-.

X 3 (1 + e L)

راه حل.اجازه دهید انتگرال در این انتگرال را با تابع مقایسه کنیم

Dg. واضح است که -r-

ایکس g* (1+0 x J

grl J-jdx همگرا می شود. بنابراین، بر اساس معیار مقایسه، 1 داده شده ایکس

انتگرال ملی

مثال 28. I-.

راه حل.مقایسه انتگرال این انتگرال با تابع 1/x،

می بینیم که (1 + در x)/x > 1/x در بازه 1

متنوع می شود، بنابراین، در مقایسه، این انتگرال نیز واگرا می شود.

در نتیجه، معیار کوشی برای همگرایی یک انتگرال نادرست از نوع اول را بدون اثبات ارائه می کنیم.

12.10.4. همگرایی مطلق و شرطی انتگرال های نامناسب

تعریف 5. یک انتگرال نامناسب J/(x)dx نامیده می شود کاملا

همگرا، اگر انتگرال J|/(x)|dx همگرا شود.

تعریف 6. انتگرال نامناسب J /(x) dx نامیده می شود مشروط مشابه

بادوام، اگر همگرا شود و انتگرال J|/(x)|dx واگرا شود.

توجه داشته باشید که همگرایی مطلق انتگرال دلالت بر همگرایی آن به دلیل تخمین 3 دارد انتگرال معینو معیار کوشی.

قضیه 12.13 (آزمون دیریکله آبل*). اجازه دهید تابع /(x) پیوسته و دارای یک پاد مشتق محدود باشد اف(x) در بازه [a، «>]، و تابع g(x) دارای مشتق پیوسته در این بازه است، افزایش نمی یابد و به صورت x -> ©o به صفر میل می کند. سپس انتگرال نامناسب

همگرا می شود.

اثباتاجازه دهید یکپارچه سازی توسط قطعات را به انتگرال J /(x)g(x)dx اعمال کنیم

در یک بخش دلخواه R R"با [ آ، °°). ما داریم:

قضیه 12.12. برای همگرا شدن انتگرال نامناسب (64/12) لازم و کافی است که برای هر e > 0 بتوان چنین عددی را پیدا کرد. آ> 0، که برای هر R"و /؟، بزرگتر از آ،نابرابری برقرار است:

با توجه به شرایط قضیه F(x)محدود، یعنی |F(x)| K. تابع g(x) افزایش نمی یابد و به صورت x -” “> به صفر میل می کند که به این معنی است. g(x)> 0، g"(x)

آبل نیلز هنریک (1802-1829) - ریاضیدان نروژی.

از آنجایی که، با توجه به شرایط قضیه، g(x) -» 0 برای x -> ©°، برای یک عدد دلخواه e > 0 می توانیم عدد را پیدا کنیم. الف>طوری که وقتی R" > Lنابرابری ارضا خواهد شد g(R") با جایگزینی این به تخمین (12.68)، به دست می آوریم:

که با معیار کوشی برای همگرایی انتگرال مطابقت دارد (66/12). قضیه ثابت شده است. ?

بیایید مثال هایی از استفاده از آزمون دیریکله آبل برای همگرایی انتگرال های نامناسب را در نظر بگیریم.

مثال 29. f^^dx, a>0.

راه حل.بیایید /(x) = گناه x را قرار دهیم، g(x)= l/x"؛ به راحتی می توان تأیید کرد که همه شرایط قضیه برآورده شده است، یعنی این انتگرال همگرا می شود. برای > 1، این انتگرال

ral کاملاً همگرا می شود. در واقع، | گناه x/xP 1/d L، انتگرال J(l/x e)dx

همگرا می شود، یعنی با معیار مقایسه (قضیه 12.11)، این انتگرال نیز به طور مطلق همگرا می شود.

مثال 30. Jsin x 2 dx - انتگرال فرنل، o

راه حل.بیایید این انتگرال را به صورت مجموع نمایش دهیم:

از آنجایی که گناه x 2 - عملکرد پیوستهدر بازه (0، 1J، اولین انتگرال در (12.69) وجود دارد. برای تعیین همگرایی انتگرال نامناسب در سمت راست (12.69)، /(x) = x sin x 2 را تنظیم می کنیم، g(x) = 1/x. سپس برای تابع /(x) ضد مشتق F(x) = -cosx 2 /!در بازه |1، ">)، محدود شده است، و #(x) مثبت است، به صورت x -" °° به صفر تمایل دارد و مشتق پیوسته ای در (1، ©о) دارد. این بدان معنی است که بر اساس معیار دیریکله- آبل، انتگرال دوم در (12.69) همگرا می شود، یعنی. انتگرال فرنل نیز همگرا می شود.

همانطور که می دانید، یافتن انتگرال می تواند کار نسبتاً دشواری باشد. شروع به محاسبه یک انتگرال نامناسب و یافتن واگرا شدن آن در انتهای مسیر، ناامیدکننده بزرگی خواهد بود. بنابراین، روش‌هایی مورد توجه هستند که اجازه می‌دهند، بدون محاسبات جدی بر اساس یک نوع تابع، در مورد همگرایی یا واگرایی یک انتگرال نامناسب نتیجه‌گیری کنیم. قضایای مقایسه اول و دوم که در ادامه مورد بحث قرار خواهد گرفت، کمک زیادی به مطالعه انتگرال های نامناسب برای همگرایی می کند.

اجازه دهید f(x)؟0. سپس توابع

به طور یکنواخت در متغیرهای t یا -g افزایش می‌یابند (از آنجایی که g>0 را می‌گیریم، -g از سمت چپ به صفر تمایل دارد). اگر با افزایش آرگومان ها، توابع F 1 (t) و F 2 (-d) از بالا محدود بمانند، به این معنی است که انتگرال های نامناسب مربوطه همگرا می شوند. این اساس اولین قضیه مقایسه برای انتگرال توابع غیر منفی است.

اجازه دهید توابع f(x) و g(x) در x?a شرایط زیر را برآورده کنند:

• 1) 0?f(x)?g(x);
• 2) توابع f(x) و g(x) پیوسته هستند.

سپس از همگرایی انتگرال، همگرایی انتگرال، و از واگرایی انتگرال، واگرایی می آید.

از آنجایی که 0?f(x)?g(x) و توابع پیوسته هستند، پس

بر اساس شرط، انتگرال همگرا می شود، یعنی. مقدار محدودی دارد بنابراین، انتگرال نیز همگرا می شود.

حالا اجازه دهید انتگرال واگرا شود. اجازه دهید فرض کنیم که انتگرال همگرا شود، اما پس از آن انتگرال باید همگرا شود، که با شرط در تضاد است. فرض ما نادرست است، انتگرال از هم جدا می شود.

قضیه مقایسه برای انتگرال های نادرست نوع دوم.

اجازه دهید برای توابع f(x) و g(x) در بازه، بدون محدودیت برای x>+0 افزایش یابد. برای x>+0، نابرابری زیر برقرار است:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.

قضیه مقایسه برای انتگرال های نادرست نوع اول.

اجازه دهید تابع f(x) و g(x) روی بازه باشد، و بخش انتگرال گیری متناهی است، یعنی با اعداد محدود می شود نه با بی نهایت. برخی از وظایف منجر به نیاز به کنار گذاشتن این محدودیت ها می شود. اینگونه است که انتگرال های نامناسب ظاهر می شوند.

معنای هندسی انتگرال نامناسبکاملاً ساده معلوم می شود. در حالتی که نمودار یک تابع y = f(ایکس) بالای محور است گاو نرانتگرال معین مساحت یک ذوزنقه منحنی را که توسط یک منحنی محدود شده است را بیان می کند. y = f(ایکس) ، محور x و مختصات ایکس = آ , ایکس = ب. به نوبه خود، انتگرال نامناسب مساحت یک ذوزنقه منحنی نامحدود (بی نهایت) محصور در بین خطوط را بیان می کند. y = f(ایکس) (در تصویر زیر - قرمز) ایکس = آو محور آبسیسا.

انتگرال های نامناسب به طور مشابه برای بازه های بی نهایت دیگر تعریف می شوند:

مساحت ذوزنقه منحنی نامتناهی می تواند عددی محدود باشد که در این صورت انتگرال نامناسب همگرا نامیده می شود. مساحت نیز می تواند بی نهایت باشد و در این حالت انتگرال نامناسب واگرا نامیده می شود.

استفاده از حد یک انتگرال به جای خود انتگرال نامناسب.برای ارزیابی انتگرال نامناسب، باید از حد انتگرال معین استفاده کنید. اگر این حد وجود داشته باشد و متناهی باشد (با بی نهایت برابر نیست)، انتگرال نامناسب همگرا و در غیر این صورت - واگرا نامیده می شود. اینکه یک متغیر در زیر علامت حد به چه تمایلی دارد بستگی به این دارد که آیا ما با یک انتگرال نامناسب از نوع اول یا نوع دوم روبرو هستیم. بیایید اکنون در این مورد بدانیم.

انتگرال های نادرست از نوع اول - با حدود بی نهایت و همگرایی آنها

انتگرال های نامناسب با حد بالایی بی نهایت

بنابراین، نوشتن یک انتگرال نامناسب با انتگرال قطعی معمول تفاوت دارد زیرا حد بالای انتگرال بی نهایت است.

تعریف. یک انتگرال نامناسب با حد بالایی بی نهایت از ادغام یک تابع پیوسته f(ایکس) در فاصله از آ قبل از ∞ حد انتگرال این تابع با حد بالایی انتگرال نامیده می شود ب و حد پایین ادغام آ مشروط بر اینکه حد بالای ادغام بدون محدودیت رشد کند، یعنی

.

اگر این حد وجود داشته باشد و برابر با عددی باشد تا بی نهایت، پس انتگرال نامناسب همگرا نامیده می شود، و عددی که حد برابر است به عنوان مقدار آن در نظر گرفته می شود. در غیر این صورت یک انتگرال نامناسب واگرا نامیده می شودو هیچ معنایی به آن نسبت داده نمی شود.

مثال 1. انتگرال نادرست را محاسبه کنید(اگر همگرا باشد).

راه حل. بر اساس تعریف انتگرال نامناسب، متوجه می شویم

از آنجایی که حد وجود دارد و برابر با 1 است، پس این است انتگرال نامناسب همگرا می شودو برابر با 1 است.

در مثال زیر انتگرال تقریباً مانند مثال 1 است، فقط درجه x دو نیست بلکه حرف آلفا است و وظیفه بررسی انتگرال نامناسب برای همگرایی است. یعنی این سوال باقی می ماند که باید پاسخ داده شود: این انتگرال نامناسب در چه مقادیری از آلفا همگرا می شود و در چه مقادیری واگرا می شود؟

مثال 2. انتگرال نامناسب را برای همگرایی بررسی کنید(حد پایین ادغام بزرگتر از صفر است).

راه حل. اجازه دهید ابتدا آن را فرض کنیم، سپس

در عبارت به دست آمده، به حد مجاز در:

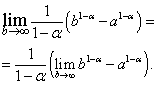
به راحتی می توان دید که حد سمت راست وجود دارد و برابر با صفر است وقتی , یعنی , و وجود ندارد وقتی , یعنی .

در حالت اول، یعنی زمانی که . اگر پس از آن و وجود ندارد

نتیجه مطالعه ما به شرح زیر است: این انتگرال نامناسب همگرا می شوددر و واگرا می شوددر .

بکارگیری فرمول نیوتن-لایبنیتس برای نوع انتگرال نامناسب مورد مطالعه ، می توانید فرمول زیر را که بسیار شبیه به آن است استخراج کنید:

.

این یک فرمول تعمیم یافته نیوتن-لایب نیتس است.

مثال 3. انتگرال نادرست را محاسبه کنید(اگر همگرا باشد).

حد این انتگرال وجود دارد:

انتگرال دوم، مجموع بیانگر انتگرال اصلی را تشکیل می دهد:

محدودیت این انتگرال نیز وجود دارد:

.

مجموع دو انتگرال را پیدا می کنیم که مقدار انتگرال نامناسب اصلی با دو حد نامتناهی است:

انتگرال های نادرست نوع دوم - از توابع نامحدود و همگرایی آنها

اجازه دهید تابع f(ایکس) داده شده در بخش از آ قبل از ب و در آن نامحدود است. فرض کنید که تابع در نقطه به بی نهایت می رود ب ، در حالی که در تمام نقاط دیگر قطعه پیوسته است.

تعریف. انتگرال نامناسب یک تابع f(ایکس) در بخش از آ قبل از ب حد انتگرال این تابع با حد بالایی انتگرال نامیده می شود ج ، اگر هنگام تلاش ج به ب تابع بدون محدودیت و در نقطه افزایش می یابد ایکس = ب تابع تعریف نشده است، یعنی

.

اگر این حد وجود داشته باشد، انتگرال نادرست نوع دوم را همگرا و در غیر این صورت واگرا می نامند.

با استفاده از فرمول نیوتن-لایبنیتس به دست می آوریم.

1. انتگرال های نامناسب با حدود بی نهایت

بیایید تعریف انتگرال را به عنوان حد مجموع انتگرال به یاد بیاوریم:

این تعریف فرض می کند که بازه ادغام محدود است و تابع f(x) درون آن پیوسته است. نقض این مفروضات منجر به انتگرال های نامناسب می شود.

تعریف.اگر انتگرال با افزایش نامحدود به حد محدودی تمایل داشته باشد "ب"، سپس این حد را یک انتگرال نامناسب با یک کران بالای بی نهایت تابع f (x) می نامند و با نماد نشان داده می شود.

در این حالت به انتگرال نامناسب گفته می شود که وجود دارد یا همگرا می شود.

اگر حد مشخص شده وجود نداشته باشد یا وجود داشته باشد اما نامتناهی باشد، آنگاه به انتگرال گفته می شود که وجود ندارد یا واگرا می شود.

یک انتگرال نامناسب با کران پایین بی نهایت به طور مشابه تعریف می شود:

یک انتگرال نامناسب با دو مرز بی نهایت به صورت زیر به دست می آید:

که در آن c هر نقطه ثابت در محور Ox است.

بنابراین، انتگرال های نامناسب می توانند یک کران پایین بی نهایت، یک کران بالای بی نهایت و همچنین دو کران نامتناهی داشته باشند.

نشانه های همگرایی همگرایی مطلق و مشروط

انتگرال فقط در صورتی وجود دارد که هر یک از انتگرال ها وجود داشته باشد: و .

مثال.همگرایی انتگرال را بررسی کنید

با فرض c = 0، دریافت می کنیم:

آن ها انتگرال همگرا می شود

گاهی اوقات نیازی به محاسبه یک انتگرال نامناسب نیست، اما کافی است با مقایسه آن با انتگرال دیگر، همگرا یا واگرایی آن را بدانید.

قضیه مقایسه برای انتگرال های نامناسب.

اگر تابع f (x) در بازه دارای چندین نقطه ناپیوستگی (تعداد متناهی) از نوع اول باشد، این "موانع" را می توان به راحتی با تقسیم قطعه به چند بخش با نقاط ناپیوستگی، محاسبه انتگرال های معین در هر بخش جدا کرد. جمع کردن نتایج

اجازه دهید انتگرال قطعی یک تابع را در نظر بگیریم که در هنگام نزدیک شدن به یکی از انتهای بخش نامحدود است، برای مثال، .

(در چنین مواردی معمولاً می گویند: "تابع دارای یک ناپیوستگی بی نهایت در انتهای سمت راست بازه ادغام است.").

واضح است که تعریف معمول انتگرال در اینجا معنای خود را از دست می دهد.

تعریف. انتگرال نامناسب تابع f(x)، پیوسته برای x £< b и неограниченной при x ® b - 0, называется предел:

انتگرال نامناسب تابعی که دارای ناپیوستگی نامتناهی در انتهای سمت چپ قطعه است به طور مشابه تعریف می شود:

در نتیجه، در بخش [-1، 0] انتگرال واگرا می شود.

این بدان معنی است که انتگرال نیز در بخش واگرا می شود.

بنابراین، این انتگرال در کل بازه [-1، 1] واگرا می شود. توجه داشته باشید که اگر بدون توجه به ناپیوستگی انتگرال در نقطه x = 0 شروع به محاسبه این انتگرال کنیم، نتیجه نادرستی می گیریم. واقعا،

، که غیر ممکن است.

بنابراین، برای مطالعه انتگرال نامناسب یک تابع ناپیوسته، باید آن را به چندین انتگرال "تقسیم" کرد و آنها را مطالعه کرد.

اگر انتگرال دارای ناپیوستگی نوع دوم در بازه (متناهی) یکپارچگی باشد، از انتگرال نادرست نوع دوم صحبت می کنیم.

10.2.1 تعریف و ویژگی های اساسی

اجازه دهید بازه ادغام را با $\left[a, \, b \right ]$ نشان دهیم؛ هر دوی این اعداد در زیر متناهی فرض می شوند. اگر فقط 1 ناپیوستگی وجود داشته باشد، می‌تواند در نقطه $a$، یا در نقطه $b$، یا درون بازه $(a,\,b)$ قرار گیرد. اجازه دهید ابتدا موردی را در نظر بگیریم که در نقطه $a$ ناپیوستگی نوع دوم وجود دارد و در نقاط دیگر تابع انتگرال پیوسته است. بنابراین ما در مورد انتگرال بحث می کنیم

\begin(معادله) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(معادله)

و $f(x) \rightarrow \infty $ وقتی $x ​​\rightarrow a+0$. مانند قبل، اولین کاری که باید انجام دهید این است که به این عبارت معنی دهید. برای این کار، انتگرال را در نظر بگیرید

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

تعریف. بگذارید یک حد محدود وجود داشته باشد

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

سپس گفته می شود که انتگرال نادرست نوع دوم (22) همگرا شده و مقدار $A$ به آن اختصاص داده می شود؛ تابع $f(x)$ خود در بازه $\left[a, \ قابل ادغام است. ، b\right]$.

اجازه دهید زمانی که یک ناپیوستگی از نوع دوم در تابع انتگرال در حد بالایی بازه ادغام وجود دارد، گزینه را در نظر بگیریم. این حالت را می توان با تغییر متغیر $x=-t$ و سپس تنظیم مجدد حدود ادغام به حالت قبلی کاهش داد.

اجازه دهید این گزینه را زمانی در نظر بگیریم که تابع انتگرال دارای ناپیوستگی نوع دوم در داخل بازه ادغام، در نقطه $c \in (a,\,b)$ باشد. در این مورد، انتگرال اصلی

\begin(معادله) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(معادله)

به صورت جمع ارائه شده است

\[ I=I_1+I_2، \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

تعریف. اگر هر دو انتگرال $I_1، \, I_2$ همگرا شوند، انتگرال نامناسب (23) همگرا نامیده می شود و مقداری برابر با مجموع انتگرال های $I_1، \, I_2$، تابع $f(x)$ به آن اختصاص می یابد. در بازه $\left [a, \, b\right]$ یکپارچه نامیده می شود. اگر حداقل یکی از انتگرال های $I_1,\, I_2$ واگرا باشد، انتگرال نامناسب (23) واگرا نامیده می شود.

انتگرال های نامناسب همگرا از نوع 2 تمام ویژگی های استاندارد انتگرال های معین معمولی را دارند.

1. اگر $f(x)$، $g(x)$ در بازه $\left[a, \,b \right ]$ قابل ادغام باشند، مجموع آنها $f(x)+g(x)$ است همچنین در این بازه قابل ادغام است و \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( ب) g (x)dx. \] 2. اگر $f(x)$ در بازه $\left[a, \, b \right ]$ قابل ادغام باشد، برای هر ثابت $C$ تابع $C\cdot f(x)$ نیز می باشد. قابل ادغام در این بازه، و \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. اگر $f(x)$ در بازه $\left[a, \, b \right ]$ و در این بازه $f(x)>0$ قابل ادغام باشد، آنگاه \[ \int _a^ (ب) f(x)dx\,>\,0. \] 4. اگر $f(x)$ در بازه $\left[a, \, b \right ]$ قابل ادغام باشد، برای هر $c\in (a, \,b)$ انتگرال \[ \ int _a^ (c) f(x)dx، \quad \int _c^(b) f(x)dx \] نیز همگرا می شوند و \[ \int _a^(b)f(x)dx=\int _a ^(c) f(x)dx+\int _c^(b) f(x)dx \] (افزایش انتگرال در بازه).

انتگرال را در نظر بگیرید

\begin(معادله) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(معادله)

اگر $k>0$، انتگرال گرایش به $\infty$ به عنوان $x \rightarrow +0$ دارد، بنابراین انتگرال از نوع دوم نامناسب است. بیایید تابع را معرفی کنیم

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

در این مورد ضد مشتق شناخته شده است، بنابراین

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

برای k \neq 1$،

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

برای k $ = 1 $. با در نظر گرفتن رفتار $\epsilon \rightarrow +0$، به این نتیجه می رسیم که انتگرال (20) در $k همگرا می شود.

10.2.2 آزمون های همگرایی انتگرال های نادرست نوع دوم

قضیه (نخستین نشانه مقایسه). اجازه دهید $f(x)$، $g(x)$ برای $x\in (a,\,b)$، و $0 1 پیوسته باشند. اگر انتگرال \[ \int _a^(b)g(x) dx \] همگرا می شود، سپس انتگرال \[ \int _a^(b)f(x)dx همگرا می شود. \] 2. اگر انتگرال \[ \int _a^(b)f(x)dx \] واگرا شود، انتگرال \[ \int _a^(b)g(x)dx واگرا می شود. \]

قضیه (ملاک مقایسه دوم). اجازه دهید $f(x)$، $g(x)$ برای $x\in (a,\,b)$ پیوسته و مثبت باشد و یک حد محدود وجود داشته باشد.

\[ \theta = \lim_(x \راست فلش a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

سپس انتگرال ها

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

به طور همزمان همگرا یا واگرا شوند.