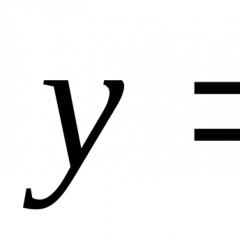Հեղափոխության մարմինների ծավալների հաշվարկման բանաձևը. Ինչպե՞ս հաշվարկել հեղափոխության մարմնի ծավալը որոշակի ինտեգրալով: Հարթ գործչի տարածք

Սահմանում 3. Հեղափոխության մարմինը այն մարմինն է, որը ստացվում է հարթ պատկերը առանցքի շուրջը պտտելով, որը չի հատում պատկերը և ընկած է նրա հետ նույն հարթության վրա:

Պտտման առանցքը կարող է հատել նկարը, եթե դա պատկերի համաչափության առանցքն է:

Թեորեմ 2.
, առանցք
և ուղիղ հատվածներ
Եվ

պտտվում է առանցքի շուրջ
. Այնուհետև արդյունքում ստացված պտտման մարմնի ծավալը կարելի է հաշվարկել բանաձևով

(2)

Ապացույց. Նման մարմնի համար խաչաձեւ հատվածը աբսցիսով շառավղով շրջան է
, Նշանակում է
և (1) բանաձևը տալիս է պահանջվող արդյունքը:

Եթե ​​թիվը սահմանափակվում է երկու շարունակական ֆունկցիաների գրաֆիկներով
Եվ
, և գծերի հատվածներ
Եվ
, և
Եվ
, ապա x առանցքի շուրջ պտտվելիս ստանում ենք մարմին, որի ծավալը

Օրինակ 3. Հաշվե՛ք տորուսի ծավալը, որը ստացվում է շրջանով սահմանափակված շրջանի պտտմամբ

abscissa առանցքի շուրջ:

Ռ որոշումը։ Ստորև նշված շրջանակը սահմանափակվում է ֆունկցիայի գրաֆիկով
և վերևից -
. Այս ֆունկցիաների քառակուսիների տարբերությունը.

Պահանջվող ծավալը

(Ինտեգրանդի գրաֆիկը վերին կիսաշրջանն է, ուստի վերևում գրված ինտեգրալը կիսաշրջանի մակերեսն է):

Օրինակ 4. Պարաբոլիկ հատված՝ հիմքով
, և բարձրությունը , պտտվում է հիմքի շուրջ։ Հաշվե՛ք ստացված մարմնի ծավալը (Կավալիերիի «կիտրոն»):

Ռ որոշումը։ Մենք կտեղադրենք պարաբոլան, ինչպես ցույց է տրված նկարում: Այնուհետև դրա հավասարումը
, և
. Գտնենք պարամետրի արժեքը :
. Այսպիսով, պահանջվող ծավալը.

Թեորեմ 3. Թող կորագիծ տրապիզը սահմանափակված լինի շարունակական ոչ բացասական ֆունկցիայի գրաֆիկով
, առանցք
և ուղիղ հատվածներ
Եվ
, և
, պտտվում է առանցքի շուրջ
. Այնուհետև ստացված պտտման մարմնի ծավալը կարելի է գտնել բանաձևով

(3)

Ապացուցման գաղափարը. Մենք բաժանում ենք հատվածը
կետեր

, մասերի և ուղիղ գծեր քաշեք
. Ամբողջ trapezoid-ը կքայքայվի շերտերի, որոնք կարելի է համարել հիմքով մոտավորապես ուղղանկյուններ
և բարձրությունը
.

Մենք կտրում ենք ստացված գլանը՝ պտտելով նման ուղղանկյունը իր գեներատորի երկայնքով և բացում այն։ Մենք ստանում ենք «գրեթե» զուգահեռաչափ՝ չափերով.
,
Եվ
. Դրա ծավալը
. Այսպիսով, հեղափոխության մարմնի ծավալի համար մենք կունենանք մոտավոր հավասարություն

Ճշգրիտ հավասարություն ստանալու համար պետք է գնալ մինչև սահմանաչափը
. Վերևում գրված գումարը ֆունկցիայի ինտեգրալ գումարն է
, հետևաբար, սահմանում մենք ստանում ենք ինտեգրալը (3) բանաձևից։ Թեորեմն ապացուցված է.

Ծանոթագրություն 1. 2-րդ և 3-րդ թեորեմներում պայմանը
կարելի է բաց թողնել. բանաձևը (2) ընդհանուր առմամբ անզգայուն է նշանի նկատմամբ
, և (3) բանաձևում դա բավարար է
փոխարինվել է
.

Օրինակ 5. Պարաբոլիկ հատված (հիմք
, բարձրություն ) պտտվում է բարձրության շուրջ: Գտե՛ք ստացված մարմնի ծավալը:

Լուծում. Տեղադրենք պարաբոլան, ինչպես ցույց է տրված նկարում: Եվ չնայած պտտման առանցքը հատում է պատկերը, այն՝ առանցքը, համաչափության առանցքն է: Հետեւաբար, մենք պետք է հաշվի առնենք հատվածի միայն աջ կեսը: Պարաբոլայի հավասարում
, և
, Նշանակում է
. Ծավալի համար մենք ունենք.

Ծանոթագրություն 2. Եթե ​​կորագիծ տրապիզոնի կորագիծ սահմանը տրված է պարամետրային հավասարումներով
,
,
Եվ
,
ապա փոխարինման հետ կարող եք օգտագործել (2) և (3) բանաձևերը վրա
Եվ
վրա
երբ այն փոխվում է տ-ից
նախքան .

Օրինակ 6. Նկարը սահմանափակվում է ցիկլոիդի առաջին աղեղով
,
,
և x առանցքը: Գտե՛ք մարմնի ծավալը, որը ստացվել է այս ցուցանիշը պտտելով՝ 1) առանցքի շուրջը
; 2) կացիններ
.

Լուծում. 1) Ընդհանուր բանաձեւ
Մեր դեպքում.

2) Ընդհանուր բանաձեւ
Մեր գործչի համար.

Հրավիրում ենք ուսանողներին ինքնուրույն կատարել բոլոր հաշվարկները։

Ծանոթագրություն 3. Թող կոր հատվածը սահմանափակված լինի շարունակական գծով
և ճառագայթներ
,

, պտտվում է բևեռային առանցքի շուրջ։ Ստացված մարմնի ծավալը կարելի է հաշվարկել բանաձևով.

Օրինակ 7. Կարդիոիդով սահմանափակված գործչի մի մասը
, շրջանից դուրս պառկած
, պտտվում է բևեռային առանցքի շուրջ։ Գտե՛ք ստացված մարմնի ծավալը:

Լուծում. Երկու գծերն էլ, և հետևաբար, նրանց սահմանած գործիչը սիմետրիկ է բևեռային առանցքի նկատմամբ: Ուստի անհրաժեշտ է դիտարկել միայն այն մասը, որի համար
. Կորերը հատվում են ժամը
Եվ

ժամը
. Այնուհետև, թիվը կարելի է համարել որպես երկու հատվածների տարբերություն, և, հետևաբար, ծավալը կարող է հաշվարկվել որպես երկու ինտեգրալների տարբերություն: Մենք ունենք:

Առաջադրանքներ անկախ որոշման համար։

1. Շրջանաձև հատված, որի հիմքը
, բարձրություն , պտտվում է հիմքի շուրջ։ Գտեք հեղափոխության մարմնի ծավալը:

2. Գտի՛ր հեղափոխության պարաբոլոիդի ծավալը, որի հիմքը , իսկ բարձրությունն է .

3. Աստրոիդով սահմանափակված պատկեր
,
պտտվում է աբսցիսայի առանցքի շուրջ: Գտե՛ք ստացված մարմնի ծավալը:

4. Գծերով սահմանափակված պատկեր
Եվ
պտտվում է x առանցքի շուրջ: Գտեք հեղափոխության մարմնի ծավալը:

Թեմա՝ «Հեղափոխության մարմինների ծավալների հաշվարկը որոշակի ինտեգրալով»

Դասի տեսակը.համակցված.

Դասի նպատակը.սովորել ինտեգրալների միջոցով հաշվարկել հեղափոխության մարմինների ծավալները:

Առաջադրանքներ.

համախմբել մի շարք երկրաչափական պատկերներից կորագիծ տրապիզոիդները բացահայտելու կարողությունը և զարգացնել կորագիծ տրապիզոիդների տարածքները հաշվարկելու հմտությունը.

ծանոթանալ եռաչափ գործչի հայեցակարգին;

սովորել հաշվարկել հեղափոխության մարմինների ծավալները.

նպաստել տրամաբանական մտածողության, գրագետ մաթեմատիկական խոսքի զարգացմանը, գծագրերի կառուցման ժամանակ ճշգրտությանը.

զարգացնել հետաքրքրություն առարկայի նկատմամբ, գործել մաթեմատիկական հասկացությունների և պատկերների հետ, զարգացնել կամք, անկախություն և հաստատակամություն վերջնական արդյունքի հասնելու համար:

Դասերի ժամանակ

I. Կազմակերպչական պահ.

Ողջույններ խմբից: Ուսանողներին հաղորդել դասի նպատակները:

Այսօրվա դասը կցանկանայի սկսել առակով. «Մի ժամանակ ապրում էր մի իմաստուն մարդ, ով գիտեր ամեն ինչ։ Մի մարդ ուզում էր ապացուցել, որ իմաստունն ամեն ինչ չգիտի։ Թիթեռը ափի մեջ բռնած՝ նա հարցրեց. «Ասա ինձ, իմաստուն, ո՞ր թիթեռնիկն է իմ ձեռքում՝ մեռա՞ծ, թե՞ ողջ»: Եվ նա մտածում է. «Եթե կենդանին ասի՝ ես կսպանեմ նրան, եթե մեռածն ասի՝ ես նրան կազատեմ»։ Իմաստունը մտածելուց հետո պատասխանեց. «Ամեն ինչ քո ձեռքերում է»:

Հետևաբար, եկեք այսօր բեղմնավոր աշխատենք, ձեռք բերենք գիտելիքների նոր պաշար և ձեռք բերած հմտություններն ու կարողությունները կկիրառենք ապագա կյանքում և գործնական գործունեության մեջ։ «Ամեն ինչ ձեր ձեռքերում է»։

II. Նախկինում ուսումնասիրված նյութի կրկնություն:

Հիշենք նախկինում ուսումնասիրված նյութի հիմնական կետերը. Դա անելու համար եկեք կատարենք «Վերացնել ավելորդ բառը» առաջադրանքը:

(Ուսանողները ասում են լրացուցիչ բառ):

Ճիշտ «Դիֆերենցիալ».Փորձեք մնացած բառերը անվանել մեկ ընդհանուր բառով: (Ամբողջական հաշվարկ):

Եկեք հիշենք ինտեգրալ հաշվարկի հետ կապված հիմնական փուլերն ու հասկացությունները:

Զորավարժություններ.Վերականգնել բացերը. (Աշակերտը դուրս է գալիս և մարկերով գրում է անհրաժեշտ բառերը):

Աշխատեք նոթատետրերում.

Նյուտոն-Լայբնից բանաձևը ստացել են անգլիացի ֆիզիկոս Իսահակ Նյուտոնը (1643-1727) և գերմանացի փիլիսոփա Գոթֆրիդ Լայբնիցը (1646-1716): Եվ դա զարմանալի չէ, քանի որ մաթեմատիկան այն լեզուն է, որով խոսում է հենց բնությունը:

Եկեք քննարկենք, թե ինչպես է այս բանաձևը օգտագործվում գործնական խնդիրներ լուծելու համար:

Օրինակ 1: Հաշվե՛ք գծերով սահմանափակված գործչի մակերեսը

Լուծում:Կառուցենք ֆունկցիաների գրաֆիկները կոորդինատային հարթության վրա . Եկեք ընտրենք գործչի տարածքը, որը պետք է գտնել:

III. Նոր նյութ սովորելը.

Ուշադրություն դարձրեք էկրանին. Ի՞նչ է պատկերված առաջին նկարում: (Նկարը ցույց է տալիս հարթ գործիչ):

Ի՞նչ է պատկերված երկրորդ նկարում: Արդյո՞ք այս ցուցանիշը հարթ է: (Նկարը ցույց է տալիս եռաչափ պատկեր):

Տիեզերքում, երկրի վրա և առօրյա կյանքում մենք հանդիպում ենք ոչ միայն հարթ պատկերների, այլև եռաչափ, բայց ինչպե՞ս կարող ենք հաշվել այդպիսի մարմինների ծավալը։ Օրինակ՝ մոլորակի, գիսաստղի, երկնաքարի ծավալը և այլն։

Մարդիկ ծավալի մասին մտածում են ինչպես տներ կառուցելիս, այնպես էլ ջուրը մի նավից մյուսը լցնելիս։ Պետք է ի հայտ գան ծավալների հաշվարկման կանոններ և տեխնիկա, այլ հարց է, թե որքանով են դրանք ճշգրիտ և հիմնավորված:

Ավստրիական Լինց քաղաքի բնակիչների համար, որտեղ ապրել է հայտնի աստղագետ Յոհաննես Կեպլերը, հատկապես խաղողի համար, 1612 թվականը շատ բեղմնավոր է եղել։ Մարդիկ պատրաստում էին գինու տակառներ և ցանկանում էին իմանալ, թե ինչպես կարելի է գործնականում որոշել դրանց ծավալները։

Այսպիսով, Կեպլերի դիտարկված աշխատանքները նշանավորեցին հետազոտությունների մի ամբողջ հոսքի սկիզբը, որը գագաթնակետին հասավ 17-րդ դարի վերջին քառորդում։ դիզայն Ի. Նյուտոնի և Գ.Վ. Դիֆերենցիալ և ինտեգրալ հաշվարկի Լայբնից. Այդ ժամանակվանից մաթեմատիկական գիտելիքների համակարգում առաջատար տեղ է գրավել փոփոխականների մաթեմատիկան։

Այսօր ես և դու զբաղվելու ենք նման գործնական գործունեությամբ, հետևաբար.

Մեր դասի թեման.

Դուք կսովորեք հեղափոխության մարմնի սահմանումը կատարելով հետևյալ առաջադրանքը.

«Լաբիրինթոս».

Զորավարժություններ.Գտեք ելք խառնաշփոթ իրավիճակից և գրեք սահմանումը:

IVԾավալների հաշվարկ.

Օգտագործելով որոշակի ինտեգրալ, դուք կարող եք հաշվարկել որոշակի մարմնի, մասնավորապես, պտտման մարմնի ծավալը:

Հեղափոխության մարմինը մարմին է, որը ստացվում է կոր trapezoid-ը իր հիմքի շուրջը պտտելով (նկ. 1, 2):

Հեղափոխության մարմնի ծավալը հաշվարկվում է բանաձևերից մեկի միջոցով:

1. OX առանցքի շուրջ:

2. , եթե կոր trapezoid-ի պտույտը op-amp-ի առանցքի շուրջ:

Աշակերտները նոթատետրում գրում են հիմնական բանաձևերը:

Ուսուցիչը բացատրում է գրատախտակին դրված օրինակների լուծումները:

1. Գտե՛ք այն մարմնի ծավալը, որը ստացվել է գծերով սահմանափակված կորագիծ տրապեզիի օրդինատային առանցքի շուրջ պտտվելուց. x2 + y2 = 64, y = -5, y = 5, x = 0:

Լուծում.

Պատասխան՝ 1163 սմ3։

2. Գտե՛ք մարմնի ծավալը, որը ստացվել է x-ի առանցքի շուրջ պարաբոլիկ տրապիզոիդը պտտելով. y =, x = 4, y = 0:

Լուծում.

Վ. Մաթեմատիկայի սիմուլյատոր.

2. Տրված ֆունկցիայի բոլոր հակաածանցյալների բազմությունը կոչվում է

Ա) անորոշ ինտեգրալ,

բ) գործառույթը,

Բ) տարբերակում.

7. Գտե՛ք այն մարմնի ծավալը, որը ստացվել է գծերով սահմանափակված կորագծային տրապեզի աբսցիսային առանցքի շուրջ պտտվելուց.

Դ/Զ. Նոր նյութի համախմբում

Հաշվե՛ք x առանցքի շուրջ ծաղկաթերթիկի պտույտից առաջացած մարմնի ծավալը y = x2, y2 = x.

Եկեք կառուցենք ֆունկցիայի գրաֆիկները։ y = x2, y2 = x. Փոխակերպենք y2 = x գրաֆիկը y = ձևի:

Մենք ունենք V = V1 - V2 Հաշվարկենք յուրաքանչյուր ֆունկցիայի ծավալը.

Եզրակացություն:

Որոշակի ինտեգրալը մաթեմատիկայի ուսումնասիրության որոշակի հիմք է, որն անփոխարինելի ներդրում ունի գործնական խնդիրների լուծման գործում։

«Ինտեգրալ» թեման հստակ ցույց է տալիս կապը մաթեմատիկայի և ֆիզիկայի, կենսաբանության, տնտեսագիտության և տեխնիկայի միջև:

Ժամանակակից գիտության զարգացումն անհնար է պատկերացնել առանց ինտեգրալի օգտագործման։ Այս առումով անհրաժեշտ է սկսել այն ուսումնասիրել միջնակարգ մասնագիտացված կրթության շրջանակներում։

VI. Գնահատում.(Մեկնաբանությամբ):

Մեծն Օմար Խայամ - մաթեմատիկոս, բանաստեղծ, փիլիսոփա: Նա խրախուսում է մեզ լինել մեր սեփական ճակատագրի տերը: Լսենք նրա ստեղծագործությունից մի հատված.

Ասում ես՝ այս կյանքը մի պահ է։
Գնահատե՛ք այն, ոգեշնչե՛ք դրանից։
Ինչպես ծախսես, այնպես էլ կանցնի։
Մի մոռացեք, որ նա ձեր ստեղծագործությունն է:

Ինտեգրալների օգտագործումը հեղափոխության մարմինների ծավալները գտնելու համար

Մաթեմատիկայի գործնական օգտակարությունը պայմանավորված է նրանով, որ առանց

Հատուկ մաթեմատիկական գիտելիքները դժվարացնում են սարքի սկզբունքները և ժամանակակից տեխնոլոգիաների կիրառումը: Յուրաքանչյուր մարդ իր կյանքում պետք է կատարի բավականին բարդ հաշվարկներ, օգտագործի սովորաբար օգտագործվող սարքավորումները, գտնի անհրաժեշտ բանաձևերը տեղեկատու գրքերում և ստեղծի պարզ ալգորիթմներ խնդիրների լուծման համար: Ժամանակակից հասարակության մեջ ավելի ու ավելի շատ մասնագիտություններ, որոնք պահանջում են բարձր մակարդակի կրթություն, կապված են մաթեմատիկայի անմիջական կիրառման հետ: Այսպիսով, մաթեմատիկան դառնում է ուսանողի համար մասնագիտորեն նշանակալի առարկա։ Առաջատար դերը պատկանում է մաթեմատիկային ալգորիթմական մտածողության ձևավորման գործում, այն զարգացնում է տվյալ ալգորիթմի համաձայն գործելու և նոր ալգորիթմներ կառուցելու կարողությունը։

Հեղափոխության մարմինների ծավալները հաշվարկելու համար ինտեգրալի օգտագործման թեման ուսումնասիրելիս ընտրովի դասարաններում սովորողներին առաջարկում եմ քննարկել թեման՝ «Հեղափոխության մարմինների ծավալները՝ օգտագործելով ինտեգրալները»։ Ստորև բերված են մեթոդաբանական առաջարկություններ այս թեմայի քննարկման համար.

1. Հարթ գործչի մակերես:

Հանրահաշվի դասընթացից գիտենք, որ գործնական բնույթի խնդիրները հանգեցրել են որոշակի ինտեգրալի հասկացությանը..gif" width="88" height="51">.jpg" width="526" height="262 src=" >

https://pandia.ru/text/77/502/images/image006_95.gif" width="127" height="25 src=">:

Ox առանցքի շուրջ կորագիծ տրապիզոնի պտույտից առաջացած պտտման մարմնի ծավալը գտնելու համար, որը սահմանափակված է y=f(x) ճեղքված գծով, Ox առանցքով, x=a և x=b ուղիղ գծերով, հաշվարկում ենք. օգտագործելով բանաձեւը

https://pandia.ru/text/77/502/images/image008_26.jpg" width="352" height="283 src=">Y

3.Գլանների ծավալը.

https://pandia.ru/text/77/502/images/image011_58.gif" width="85" height="51">..gif" width="13" height="25">..jpg" width="401" height="355">Կոնը ստացվում է ABC ուղղանկյուն եռանկյունը (C = 90) պտտելով Ox առանցքի շուրջ, որի վրա ընկած է AC ոտքը:

AB հատվածը գտնվում է y=kx+c ուղիղ գծի վրա, որտեղ https://pandia.ru/text/77/502/images/image019_33.gif" width="59" height="41 src=">:

Թող a=0, b=H (H-ը կոնի բարձրությունն է), ապա Vhttps://pandia.ru/text/77/502/images/image021_27.gif" width="13" height="23 src= «>.

5.Կտրված կոնի ծավալը:

Կտրված կոն կարելի է ձեռք բերել՝ Ox առանցքի շուրջ ուղղանկյուն ABCD (CDOx) պտտելով:

AB հատվածն ընկած է y=kx+c ուղիղ գծի վրա, որտեղ , c=r.

Քանի որ ուղիղ գիծն անցնում է A կետով (0;r):

Այսպիսով, ուղիղ գիծը նման է https://pandia.ru/text/77/502/images/image027_17.gif" width="303" height="291 src=">

Թող a=0, b=H (H-ը կտրված կոնի բարձրությունն է), ապա https://pandia.ru/text/77/502/images/image030_16.gif" width="36" height="17 src" ="> = .

6. Գնդակի ծավալը.

Գնդակը կարելի է ստանալ՝ Ox առանցքի շուրջ (0;0) կենտրոնով շրջան պտտելով: Ox առանցքի վերևում գտնվող կիսաշրջանը տրված է հավասարմամբ

https://pandia.ru/text/77/502/images/image034_13.gif" width="13" height="16 src=">x Ռ.

Դասի տեսակը՝ համակցված։

Դասի նպատակը.սովորել ինտեգրալների միջոցով հաշվարկել հեղափոխության մարմինների ծավալները:

Առաջադրանքներ.

• համախմբել մի շարք երկրաչափական պատկերներից կորագիծ տրապիզոիդները բացահայտելու կարողությունը և զարգացնել կորագիծ տրապիզոիդների տարածքները հաշվարկելու հմտությունը.
• ծանոթանալ եռաչափ գործչի հայեցակարգին;
• սովորել հաշվարկել հեղափոխության մարմինների ծավալները.
• նպաստել տրամաբանական մտածողության, գրագետ մաթեմատիկական խոսքի զարգացմանը, գծագրերի կառուցման ժամանակ ճշգրտությանը.
• զարգացնել հետաքրքրություն առարկայի նկատմամբ, մաթեմատիկական հասկացությունների և պատկերների հետ գործելու, վերջնական արդյունքի հասնելու կամք, անկախություն և հաստատակամություն զարգացնել:

Դասերի ժամանակ

I. Կազմակերպչական պահ.

Ողջույններ խմբից: Ուսանողներին հաղորդել դասի նպատակները:

Արտացոլում. Հանգիստ մեղեդի.

– Այսօրվա դասը կուզենայի սկսել առակով. «Մի ժամանակ ապրում էր մի իմաստուն մարդ, ով գիտեր ամեն ինչ։ Մի մարդ ուզում էր ապացուցել, որ իմաստունն ամեն ինչ չգիտի։ Թիթեռը ափի մեջ բռնած՝ նա հարցրեց. «Ասա ինձ, իմաստուն, ո՞ր թիթեռնիկն է իմ ձեռքում՝ մեռա՞ծ, թե՞ ողջ»: Իսկ ինքը մտածում է. «Եթե կենդանին ասի՝ կսպանեմ, մեռածը կասի՝ կազատեմ»։ Իմաստունը մտածելուց հետո պատասխանեց. «Ամեն ինչ ձեր ձեռքերում է». (Ներկայացում.Սլայդ)

– Հետևաբար, եկեք այսօր բեղմնավոր աշխատենք, ձեռք բերենք գիտելիքների նոր պաշար և ձեռք բերված հմտություններն ու կարողությունները կկիրառենք ապագա կյանքում և գործնական գործունեության մեջ։ «Ամեն ինչ ձեր ձեռքերում է».

II. Նախկինում ուսումնասիրված նյութի կրկնություն:

– Հիշենք նախկինում ուսումնասիրված նյութի հիմնական կետերը: Դա անելու համար եկեք ավարտենք առաջադրանքը «Վերացրեք ավելորդ բառը»:(Սլայդ.)

(Աշակերտը գնում է I.D.-ն օգտագործում է ռետին՝ ավելորդ բառը հեռացնելու համար):

- Ճիշտ «Դիֆերենցիալ». Փորձեք մնացած բառերը անվանել մեկ ընդհանուր բառով: (Ամբողջական հաշվարկ):

– Եկեք հիշենք ինտեգրալ հաշվարկի հետ կապված հիմնական փուլերն ու հասկացությունները:

«Մաթեմատիկական փունջ».

Զորավարժություններ. Վերականգնել բացերը. (Աշակերտը դուրս է գալիս և գրիչով գրում է անհրաժեշտ բառերը):

– Ինտեգրալների կիրառման մասին վերացական կլսենք ավելի ուշ:

Աշխատեք նոթատետրերում.

– Նյուտոն-Լայբնից բանաձևը ստացվել է անգլիացի ֆիզիկոս Իսահակ Նյուտոնի (1643–1727) և գերմանացի փիլիսոփա Գոթֆրիդ Լայբնիցի (1646–1716) կողմից։ Եվ դա զարմանալի չէ, քանի որ մաթեմատիկան այն լեզուն է, որով խոսում է հենց բնությունը:

- Եկեք դիտարկենք, թե ինչպես է այս բանաձևը օգտագործվում գործնական խնդիրներ լուծելու համար:

Օրինակ 1: Հաշվե՛ք գծերով սահմանափակված գործչի մակերեսը

Լուծում. Կառուցենք ֆունկցիաների գրաֆիկները կոորդինատային հարթության վրա . Եկեք ընտրենք գործչի տարածքը, որը պետք է գտնել:

III. Նոր նյութ սովորելը.

- Ուշադրություն դարձրեք էկրանին: Ի՞նչ է պատկերված առաջին նկարում: (Սլայդ) (Նկարը ցույց է տալիս հարթ գործիչ):

- Ի՞նչ է պատկերված երկրորդ նկարում: Արդյո՞ք այս ցուցանիշը հարթ է: (Սլայդ) (Նկարը ցույց է տալիս եռաչափ պատկեր):

– Տիեզերքում, երկրի վրա և առօրյա կյանքում մենք հանդիպում ենք ոչ միայն հարթ պատկերների, այլև եռաչափ, բայց ինչպե՞ս կարող ենք հաշվել այդպիսի մարմինների ծավալը։ Օրինակ՝ մոլորակի, գիսաստղի, երկնաքարի ծավալը և այլն։

– Մարդիկ մտածում են ծավալի մասին և՛ տներ կառուցելիս, և՛ ջուրը մի նավից մյուսը լցնելիս: Պետք է ի հայտ գան ծավալների հաշվարկման կանոններ և տեխնիկա, այլ հարց է, թե որքանով են դրանք ճշգրիտ և ողջամիտ:

Ուղերձ ուսանողից. (Տյուրինա Վերա.)

Ավստրիական Լինց քաղաքի բնակիչների համար, որտեղ ապրել է հայտնի աստղագետ Յոհաննես Կեպլերը, հատկապես խաղողի համար, 1612 թվականը շատ բեղմնավոր է եղել։ Մարդիկ պատրաստում էին գինու տակառներ և ցանկանում էին իմանալ, թե ինչպես կարելի է գործնականում որոշել դրանց ծավալները։ (Սլայդ 2)

– Այսպիսով, Կեպլերի դիտարկված աշխատանքները հիմք դրեցին հետազոտությունների մի ամբողջ հոսքի, որը գագաթնակետին հասավ 17-րդ դարի վերջին քառորդում: դիզայն Ի. Նյուտոնի և Գ.Վ. Դիֆերենցիալ և ինտեգրալ հաշվարկի Լայբնից. Այդ ժամանակվանից մաթեմատիկական գիտելիքների համակարգում առաջատար տեղ է գրավում փոփոխականների մաթեմատիկան։

«Այսօր ես և դու զբաղվելու ենք նման գործնական գործունեությամբ, հետևաբար.

Մեր դասի թեման. (Սլայդ)

– Դուք կսովորեք պտտման մարմնի սահմանումը կատարելով հետևյալ առաջադրանքը.

«Լաբիրինթոս».

Լաբիրինթ (հունարեն բառ) նշանակում է գետնի տակ մտնել։ Լաբիրինթոսը արահետների, անցումների և փոխկապակցված սենյակների բարդ ցանց է:

Բայց սահմանումը «կոտրվեց»՝ թողնելով հետքեր՝ նետերի տեսքով:

Զորավարժություններ. Գտեք ելք խառնաշփոթ իրավիճակից և գրեք սահմանումը:

Սլայդ. «Քարտեզի հրահանգ» Ծավալների հաշվարկ.

Օգտագործելով որոշակի ինտեգրալ, դուք կարող եք հաշվարկել որոշակի մարմնի, մասնավորապես, պտտման մարմնի ծավալը:

Հեղափոխության մարմինը մարմին է, որը ստացվում է կոր trapezoid-ը իր հիմքի շուրջը պտտելով (նկ. 1, 2):

Պտտման մարմնի ծավալը հաշվարկվում է բանաձևերից մեկի միջոցով.

1. OX առանցքի շուրջ:

2. , եթե կոր trapezoid-ի պտույտը op-amp-ի առանցքի շուրջ:

Յուրաքանչյուր ուսանող ստանում է հրահանգչական քարտ: Ուսուցիչը շեշտում է հիմնական կետերը.

– Ուսուցիչը բացատրում է գրատախտակին դրված օրինակների լուծումները:

Դիտարկենք մի հատված Ա. Ս. Պուշկինի հայտնի հեքիաթից «Ցար Սալթանի հեքիաթը, նրա փառահեղ և հզոր որդու՝ արքայազն Գվիդոն Սալտանովիչի և գեղեցկուհի Արքայադուստր Կարապի հեքիաթը» (Սլայդ 4):

…..
Եվ հարբած սուրհանդակը բերեց
Նույն օրը կարգը հետևյալն է.
«Թագավորը պատվիրում է իր տղաներին.
Առանց ժամանակ կորցնելու,
Եվ թագուհին և սերունդը
Գաղտնի նետել ջրի անդունդը»։
Անելիք չկա. տղաներ,
Անհանգստանալով ինքնիշխանի համար
Եվ երիտասարդ թագուհուն,
Նրա ննջասենյակ եկավ բազմություն։
Նրանք հայտարարեցին թագավորի կամքը.
Նա և իր որդին չար բաժին ունեն,
Մենք բարձրաձայն կարդում ենք հրամանագիրը.
Իսկ թագուհին նույն ժամին
Ինձ տղայիս հետ տակառի մեջ դրեցին,
Կտրեցին ու քշեցին
Եվ նրանք ինձ թույլ տվեցին մտնել օկիյան,
Ահա թե ինչ է պատվիրել ցար Սալթանը.

Որքա՞ն պետք է լինի տակառի ծավալը, որպեսզի թագուհին և նրա որդին տեղավորվեն դրա մեջ։

- Հաշվի առեք հետևյալ առաջադրանքները

1. Գտե՛ք այն մարմնի ծավալը, որը ստացվել է գծերով սահմանափակված կորագիծ տրապեզիի օրդինատային առանցքի շուրջ պտտվելուց. x 2 + y 2 = 64, y = -5, y = 5, x = 0:

Պատասխան՝ 1163 սմ 3 .

Գտե՛ք մարմնի ծավալը, որը ստացվել է պարաբոլիկ տրապեզոիդը աբսցիսային առանցքի շուրջ պտտելով y =, x = 4, y = 0:

IV. Նոր նյութի համախմբում

Օրինակ 2. Հաշվե՛ք x առանցքի շուրջ ծաղկաթերթի պտույտից առաջացած մարմնի ծավալը. y = x 2, y 2 = x:

Եկեք կառուցենք ֆունկցիայի գրաֆիկները։ y = x 2, y 2 = x. Ժամանակացույց y2 = xվերածել ձևի y= .

Մենք ունենք V = V 1 – V 2Եկեք հաշվարկենք յուրաքանչյուր ֆունկցիայի ծավալը

Հիմա եկեք նայենք Մոսկվայի ռադիոկայանի աշտարակին Շաբոլովկայում, որը կառուցվել է նշանավոր ռուս ինժեներ, պատվավոր ակադեմիկոս Վ.Գ. Շուխովի նախագծով: Այն բաղկացած է մասերից՝ պտտման հիպերբոլոիդներից։ Ընդ որում, դրանցից յուրաքանչյուրը պատրաստված է հարակից շրջանակները միացնող ուղիղ մետաղյա ձողերից (նկ. 8, 9):

- Եկեք դիտարկենք խնդիրը.

Գտե՛ք մարմնի ծավալը, որը ստացվել է հիպերբոլային աղեղների պտտմամբ իր երևակայական առանցքի շուրջ, ինչպես ցույց է տրված Նկ. 8, որտեղ

խորանարդ միավորներ

Խմբային առաջադրանքներ. Սովորողները առաջադրանքներով վիճակահանություն են անում, Whatman թղթի վրա նկարներ են անում, իսկ խմբի ներկայացուցիչներից մեկը պաշտպանում է աշխատանքը:

1-ին խումբ.

Հարվածե՛ք Հարվածե՛ք Եվս մեկ հարված.
Գնդակը թռչում է դեպի դարպասը - ԳՆԴԱԿ:
Եվ սա ձմերուկի գնդակ է
Կանաչ, կլոր, համեղ։
Ավելի լավ նայեք, ինչ գնդակ:
Այն կազմված է ոչ այլ ինչից, բացի շրջանակներից։
Ձմերուկը շրջանաձև կտրատել
Եվ համտեսեք դրանք:

Գտե՛ք մարմնի ծավալը, որը ստացվել է սահմանափակ ֆունկցիայի OX առանցքի շուրջ պտտվելով

Սխալ. Էջանիշը սահմանված չէ:

- Խնդրում եմ, ասեք, թե որտեղ ենք մենք հանդիպում այս ցուցանիշին:

Տուն. առաջադրանք 1 խմբի համար. ԳԼՈՆ (Սլայդ) .

«Գլան - ինչ է դա»: – հարցրի հայրիկիս:
Հայրը ծիծաղեց. Գլխարկը գլխարկ է:
Ճիշտ պատկերացում ունենալու համար,
Մխոցը, ասենք, թիթեղյա տարա է։
Շոգենավի խողովակ - գլան,
Մեր տանիքի խողովակը նույնպես,

Բոլոր խողովակները նման են գլան:
Եվ ես այսպիսի օրինակ բերեցի.
Իմ սիրելի կալեիդոսկոպ,
Չես կարող աչքդ կտրել նրանից,
Եվ այն նաև նման է մխոցի:

- Մարզվել. Տնային առաջադրանք՝ գծապատկերե՛ք ֆունկցիան և հաշվարկե՛ք ծավալը։

2-րդ խումբ. ԿՈՆ (Սլայդ).

Մայրիկը ասաց. Եվ հիմա
Իմ պատմությունը կլինի կոնի մասին:
Stargazer բարձր գլխարկով
Ամբողջ տարին հաշվում է աստղերը:
ԿՈՆ - աստղադիտողի գլխարկ:
Ահա թե ինչպիսին է նա։ Հասկացա՞ր: վերջ։
Մայրիկը կանգնած էր սեղանի մոտ,
Ես յուղ եմ լցրել շշերի մեջ։
-Որտե՞ղ է ձագարը: Ձագար չկա:
Փնտրեք այն: Մի կանգնեք կողքի վրա:
- Մայրիկ, ես չեմ շարժվի:
Ասա ինձ ավելի շատ կոնի մասին:
– Ձագարը ջրցանի կոնի տեսքով է։
Արի, արագ գտիր նրան ինձ համար:
Ես չկարողացա գտնել ձագարը
Բայց մայրիկը պայուսակ պատրաստեց,
Ստվարաթուղթը փաթաթեցի մատիս շուրջը
Եվ նա հմտորեն ամրացրեց այն թղթի սեղմակով:
Յուղը հոսում է, մայրիկը ուրախ է,
Կոնը ճիշտ դուրս եկավ:

Զորավարժություններ. Հաշվե՛ք աբսցիսային առանցքի շուրջ պտտվելով ստացված մարմնի ծավալը

Տուն. առաջադրանք 2-րդ խմբի համար. ԲՈՒՐԳ(Սլայդ).

Ես տեսա նկարը։ Այս նկարում
Ավազոտ անապատում ԲՈՒՐԳ կա։
Բուրգում ամեն ինչ արտասովոր է,
Նրա մեջ ինչ-որ առեղծված ու առեղծված կա։
Եվ Սպասկայա աշտարակը Կարմիր հրապարակում
Այն շատ ծանոթ է ինչպես երեխաներին, այնպես էլ մեծահասակներին:
Եթե ​​նայեք աշտարակին, այն սովորական է թվում,
Ի՞նչ կա դրա վերևում: Բուրգ!

Զորավարժություններ.Տնային առաջադրանք՝ գծե՛ք ֆունկցիան և հաշվարկե՛ք բուրգի ծավալը

– Մենք հաշվարկել ենք տարբեր մարմինների ծավալները՝ հիմնվելով մարմինների ծավալների հիմնական բանաձևի վրա՝ օգտագործելով ինտեգրալ:

Սա ևս մեկ հաստատում է, որ որոշակի ինտեգրալը որոշակի հիմք է մաթեմատիկայի ուսումնասիրության համար:

-Դե հիմա մի քիչ հանգստանանք։

Գտեք զույգ:

Մաթեմատիկական դոմինոյի մեղեդին նվագում է:

«Ճանապարհը, որը ես ինքս փնտրում էի, երբեք չի մոռացվի…»

Հետազոտական ​​աշխատանք. Ինտեգրալի կիրառումը տնտեսագիտության և տեխնոլոգիայի մեջ.

Թեստեր ուժեղ ուսանողների համար և մաթեմատիկական ֆուտբոլ:

Մաթեմատիկայի սիմուլյատոր.

2. Տրված ֆունկցիայի բոլոր հակաածանցյալների բազմությունը կոչվում է

Ա) անորոշ ինտեգրալ,

բ) գործառույթը,

Բ) տարբերակում.

7. Գտե՛ք գծերով սահմանափակված կորագծային տրապիզոնի աբսցիսային առանցքի շուրջ պտտվելուց ստացված մարմնի ծավալը.

Դ/Զ. Հաշվեք հեղափոխության մարմինների ծավալները:

Արտացոլում.

Արտացոլման ընդունումը ձևով համաժամանակացում(հինգ տող):

1-ին տող – թեմայի անվանումը (մեկ գոյական):

2-րդ տող – թեմայի նկարագրությունը երկու բառով, երկու ածականով:

3-րդ տող – այս թեմայի շրջանակներում կատարվող գործողությունների նկարագրությունը երեք բառով:

4-րդ տողը չորս բառից բաղկացած արտահայտություն է, որը ցույց է տալիս վերաբերմունքը թեմային (մի ամբողջ նախադասություն):

5-րդ տողը հոմանիշ է, որը կրկնում է թեմայի էությունը։

1. Ծավալը.
2. Որոշակի ինտեգրալ, ինտեգրվող ֆունկցիա:
3. Մենք կառուցում ենք, պտտվում ենք, հաշվարկում ենք։
4. Մարմին, որը ստացվում է կոր trapezoid-ի պտտմամբ (նրա հիմքի շուրջը)։
5. Պտտման մարմին (ծավալային երկրաչափական մարմին):

Եզրակացություն (Սլայդ).

• Որոշակի ինտեգրալը մաթեմատիկայի ուսումնասիրության որոշակի հիմք է, որն անփոխարինելի ներդրում է կատարում գործնական խնդիրների լուծման գործում։
• «Ինտեգրալ» թեման հստակ ցույց է տալիս կապը մաթեմատիկայի և ֆիզիկայի, կենսաբանության, տնտեսագիտության և տեխնիկայի միջև:
• Ժամանակակից գիտության զարգացումն անհնար է պատկերացնել առանց ինտեգրալի օգտագործման։ Այս առումով անհրաժեշտ է սկսել այն ուսումնասիրել միջնակարգ մասնագիտացված կրթության շրջանակներում։

Գնահատում. (Մեկնաբանությամբ):

Մեծն Օմար Խայամ - մաթեմատիկոս, բանաստեղծ, փիլիսոփա: Նա խրախուսում է մեզ լինել մեր սեփական ճակատագրի տերը: Լսենք նրա ստեղծագործությունից մի հատված.

Կասեք՝ այս կյանքը մի պահ է։
Գնահատե՛ք այն, ոգեշնչե՛ք դրանից։
Ինչպես ծախսես, այնպես էլ կանցնի։
Մի մոռացեք, որ նա ձեր ստեղծագործությունն է: