Ի՞նչ է հավասարումը:

Նրանք, ովքեր առաջին քայլերն են անում հանրահաշվում, բնականաբար, պահանջում են նյութի ամենադժվար ներկայացումը։ Հետևաբար, մեր հոդվածում այն ​​մասին, թե ինչ է հավասարումը, մենք ոչ միայն կտանք սահմանում, այլև օրինակներով կտանք հավասարումների տարբեր դասակարգումներ։

Ինչ է հավասարումը: Ընդհանուր հասկացություններ

Այսպիսով, հավասարումը անհայտի հետ հավասարության տեսակ է, որը նշվում է լատինատառով: Այս դեպքում այս տառի թվային արժեքը, որը թույլ է տալիս մեզ ստանալ ճիշտ հավասարություն, կոչվում է հավասարման արմատ: Այս մասին ավելին կարող եք կարդալ մեր հոդվածում, բայց մենք կշարունակենք խոսել հենց հավասարումների մասին: Հավասարման (կամ փոփոխականների) փաստարկներն անհայտ են, և հավասարման լուծումը նրա բոլոր արմատների կամ արմատների բացակայությունն է:

Հավասարումների տեսակները

Հավասարումները բաժանվում են երկու մեծ խմբի՝ հանրահաշվական և տրանսցենդենտալ։

• Հանրահաշվական հավասարումն այն հավասարումն է, որտեղ հավասարման արմատը գտնելու համար օգտագործվում են միայն հանրահաշվական գործողություններ՝ 4 թվաբանական, ինչպես նաև բնական արմատի աստիճանականացում և արդյունահանում։
• Տրանսցենդենտալ հավասարումը այն հավասարումն է, որտեղ արմատը գտնելու համար օգտագործվում են ոչ հանրահաշվական ֆունկցիաներ՝ օրինակ՝ եռանկյունաչափական, լոգարիթմական և այլն։

Հանրահաշվական հավասարումների շարքում կան նաև.

• ամբողջ թվեր - երկու մասերով, որոնք բաղկացած են ամբողջ հանրահաշվական արտահայտություններից անհայտների հետ կապված.
• կոտորակային - պարունակող ամբողջ թվային հանրահաշվական արտահայտություններ համարիչում և հայտարարում.
• իռացիոնալ - հանրահաշվական արտահայտություններն այստեղ արմատային նշանի տակ են:

Նկատի ունեցեք նաև, որ կոտորակային և իռացիոնալ հավասարումները կարող են կրճատվել մինչև ամբողջական հավասարումներ լուծել:

Տրանսցենդենտալ հավասարումները բաժանվում են.

• Էքսպոնենցիալ հավասարումները հավասարումներ են, որոնք որպես ցուցիչ պարունակում են փոփոխական։ Դրանք լուծվում են մեկ հիմքի կամ ցուցիչի անցնելու միջոցով՝ փակագծերից հանելով ընդհանուր գործակիցը, ֆակտորինգը և որոշ այլ մեթոդներ;
• լոգարիթմական - լոգարիթմներով հավասարումներ, այսինքն՝ հավասարումներ, որտեղ անհայտները գտնվում են հենց լոգարիթմների ներսում: Նման հավասարումների լուծումը շատ դժվար է (ի տարբերություն, ասենք, հանրահաշվականների մեծամասնության), քանի որ դա պահանջում է ամուր մաթեմատիկական պատրաստվածություն: Այստեղ ամենակարևորը լոգարիթմներով հավասարումից անցնելն է առանց դրանց հավասարման, այսինքն՝ պարզեցնել հավասարումը (լոգարիթմների հեռացման այս մեթոդը կոչվում է հզորացում)։ Իհարկե, հնարավոր է հզորացնել լոգարիթմական հավասարումը միայն այն դեպքում, եթե դրանք ունեն միանման թվային հիմքեր և չունեն գործակիցներ.
• Եռանկյունաչափական հավասարումները եռանկյունաչափական ֆունկցիաների նշանների տակ գտնվող փոփոխականներով հավասարումներ են: Դրանց լուծումը պահանջում է եռանկյունաչափական ֆունկցիաների նախնական տիրապետում;
• խառը տարբերակված հավասարումներ են տարբեր տեսակներին պատկանող մասերով (օրինակ՝ պարաբոլիկ և էլիպսային մասերով կամ էլիպսային և հիպերբոլիկ և այլն)։

Ինչ վերաբերում է անհայտների քանակով դասակարգմանը, ապա ամեն ինչ պարզ է՝ տարբերվում են մեկ, երկու, երեք և այլն անհայտներով հավասարումներ։ Կա նաև մեկ այլ դասակարգում, որը հիմնված է այն աստիճանի վրա, որը գտնվում է բազմանդամի ձախ կողմում։ Դրա հիման վրա առանձնանում են գծային, քառակուսի և խորանարդ հավասարումներ։ Գծային հավասարումներ կարելի է անվանել նաև 1-ին աստիճանի, քառակուսային՝ 2-րդ և համապատասխանաբար 3-րդ աստիճանի հավասարումներ։ Դե, հիմա բերենք այս կամ այն ​​խմբի հավասարումների օրինակներ:

Տարբեր տեսակի հավասարումների օրինակներ

Հանրահաշվական հավասարումների օրինակներ.

• կացին + b= 0
• ax 3 + bx 2 + cx+ d= 0
• կացին 4 + bx 3 + cx 2 + bx + a= 0
  (a-ն հավասար չէ 0-ի)

Տրանսցենդենտալ հավասարումների օրինակներ.

• cos x = x log x = x−5 2 x = logx+x 5 +40

Ամբողջական հավասարումների օրինակներ.

• (2+x)2 = (2+x)(55x-4) (x2-12x+10)4 = (3x+10)4 (4x2+3x-10)2=9x4

Կոտորակի հավասարումների օրինակ.

• 15 x + — = 5x - 17 x

Իռացիոնալ հավասարումների օրինակ.

• √2kf(x)=g(x)

Գծային հավասարումների օրինակներ.

• 2x+7=0 x - 3 = 2 - 4x 2x+3=5x+5 - 3x - 2

Քառակուսային հավասարումների օրինակներ.

• x 2 +5x−7= 0 3x 2 +5x−7= 0 11x 2 −7x+3 = 0

Խորանարդային հավասարումների օրինակներ.

• x 3 -9x 2 -46x+120=0 x 3 - 4x 2 + x + 6 = 0

Էքսպոնենցիալ հավասարումների օրինակներ.

• 5 x+2 = 125 3 x 2 x = 8 x+3 3 2x +4 3 x -5 = 0

Լոգարիթմական հավասարումների օրինակներ.

• log 2 x= 3 log 3 x= -1

Եռանկյունաչափական հավասարումների օրինակներ.

• 3sin 2 x + 4sin x cosx + cos 2 x = 2 sin(5x+π/4) = ctg(2x-π/3) sinx + cos 2 x + tan 3 x = ctg 4 x

Խառը հավասարումների օրինակներ.

• log x (log 9 (4⋅3 x −3))=1 |5x−8|+|2⋅5x+3|=13

Մնում է ավելացնել, որ տարբեր տիպի հավասարումներ լուծելու համար օգտագործվում են տարբեր մեթոդներ։ Դե, գրեթե ցանկացած հավասարումներ լուծելու համար ձեզ հարկավոր կլինի ոչ միայն հանրահաշվի, այլև եռանկյունաչափության, հաճախ նաև շատ խորը գիտելիքներ:

Մաթեմատիկա. Հանրահաշիվ. Երկրաչափություն. Եռանկյունաչափություն

ՀԱՇՎԱՌՈՒՄ. Հավասարումներ և հավասարումների համակարգեր

4.2. Հավասարումների տեսակները և դրանց լուծման մեթոդները

Այն դեպքում, երբ անհրաժեշտ է գտնել փոփոխականի արժեքները, որոնք բավարարում են տվյալ երկու հավասարումները, մենք ասում ենք, որ այն տրված է. հավասարումների համակարգ. Գանգուր ամրացումն օգտագործվում է համակարգը ցույց տալու համար.

Մի քանի հավասարումներ մեկ փոփոխական ձևով հավասարումների հավաքածու, եթե խնդիրն է գտնել փոփոխականի բոլոր այն արժեքները, որոնցից յուրաքանչյուրը այս հավասարումներից առնվազն մեկի արմատն է: Բնակչությունը նշելու համար օգտագործվում է քառակուսի փակագիծ.

Մոդուլի նշանի տակ փոփոխական պարունակող հավասարումներ:

Թվի բացարձակ արժեքը Ասահմանվում է հետևյալ կերպ.

Օրինակ. Լուծե՛ք հավասարումը

.

Լուծում. Եթե

, Դա . Կարող եք գրել այսպես.

From Eq.

մենք գտնում ենք X= -9. Այնուամենայնիվ, փոփոխականի այս արժեքի դեպքում անհավասարությունը չի պահպանվում, ինչը նշանակում է, որ հայտնաբերված արժեքը այս հավասարման արմատը չէ:, Դա և այս հավասարումը կունենա ձև. Կարող եք գրել այսպես.

From Eq.

մենք գտնում ենք. Անհավասարությունը ճիշտ է, ինչը նշանակում է - այս հավասարման արմատը:.

Հավասարումներ՝ հայտարարի մեջ փոփոխականով:

Դիտարկենք ձևի հավասարումները

. (1)

(1) տիպի հավասարման լուծումը հիմնված է հետևյալ դրույթի վրա՝ կոտորակը հավասար է 0-ի, եթե և միայն այն դեպքում, եթե նրա համարիչը հավասար է 0-ի, իսկ հայտարարը՝ ոչ զրոյի:

Համաձայն վերոհիշյալի, հավասարման լուծումը

իրականացվում է երկու փուլով՝ նախ պետք է լուծել հավասարումըև այնուհետև պարզեք, թե արդյոք փոփոխականի գտնված արժեքներով, Xհայտարարժամը 0. Եթե q(x) ¹ 0 , ապա հավասարման հայտնաբերված արմատընաև (1) հավասարման արմատն է. Եթեq(x) = 0, ապա ստացված հավասարման արմատընաև (1) հավասարման արմատն է։ Ստացված համակարգը հետևյալն է.

Հավասարման տիրույթ

f(x) = g(x) կանչել փոփոխականի այդ բոլոր արժեքների բազմությունը X, որի համար արտահայտությունըf(x), և արտահայտությունը g(x)իմաստալի.

Եթե ​​հավասարման փոխակերպման գործընթացում նրա սահմանման տիրույթն ընդլայնվել է, ապա կարող են առաջանալ կողմնակի արմատներ։ Հետևաբար, փոփոխականի բոլոր գտնված արժեքները պետք է ստուգվեն սկզբնական հավասարման մեջ փոխարինմամբ կամ սկզբնական հավասարման սահմանման տիրույթով:

Ռացիոնալ հավասարումներ.

Հավասարումը

f(x) = g(x) կանչեց ռացիոնալ, Եթե f(x) և g(x)- ռացիոնալ արտահայտություններ. Ընդ որում, եթե f(x) և g(x)- ամբողջ արտահայտություններ, ապա կոչվում է հավասարումը ամբողջ ;եթե արտահայտություններից գոնե մեկըf(x), g(x)կոտորակային է, ապա ռացիոնալ հավասարումըf(x) = g(x) կանչեց կոտորակային .

Ռացիոնալ հավասարումը լուծելու համար անհրաժեշտ է.

1. գտնել բոլոր հասանելի կոտորակների ընդհանուր հայտարարը.
2. փոխարինել այս հավասարումը ամբողջականով, դրա երկու մասերը բազմապատկելով ընդհանուր հայտարարով.
3. Լուծեք ստացված ամբողջ հավասարումը;
4. Իր արմատներից վերացրեք նրանց, որոնք ընդհանուր հայտարարը վերացնում են։

Հավասարման լուծում

p(x) = 0 ֆակտորացման մեթոդ. p(x) կարող է ֆակտորիզացվել. , ապա հավասարումըվերցնում է ձևը . Եթե Ա- հավասարման արմատը, Դա , հետևաբար թվերից գոնե մեկըհավասար է 0-ի:

Ճիշտ է նաև հակառակը՝ եթե X

= Ա- հավասարումներից առնվազն մեկի արմատը, , Դա Ա- հավասարման արմատը. Այն է

Հավասարումների լուծում

ներմուծելով նոր փոփոխական.

Եկեք բացատրենք մեթոդի էությունը օրինակով.

Օրինակ. Լուծե՛ք հավասարումը

.

Լուծում Եկեք դնենք

, ստանում ենք հավասարումը, որտեղ մենք գտնում ենք . Խնդիրը հանգում է մի շարք հավասարումների լուծմանը

Û

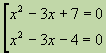
Առաջին քառակուսի հավասարումը չունի իրական արմատներ, ուստի դրա դիսկրիմինանտը բացասական է: Երկրորդից մենք գտնում ենք

. Սրանք տրված հավասարման արմատներն են։

Ձևի հավասարումը կոչվում է երկքառակուսի

, Որտեղ Ա ¹ 0. Երկ քառակուսի հավասարումը լուծվում է նոր փոփոխական ներմուծելով.դնելով , մենք հասնում ենք քառակուսային հավասարմանը .

Իռացիոնալ հավասարումներ.

Իռացիոնալ

հավասարում է, որում փոփոխականը պարունակվում է արմատի նշանի տակ կամ կոտորակային հզորության բարձրացման նշանի տակ։ Նման հավասարումների լուծման եղանակներից մեկը հավասարման երկու կողմերը նույն ուժի վրա բարձրացնելու մեթոդն է.

Ա) տրված իռացիոնալ հավասարումը վերածել ձևի:

;

Բ) մենք բարձրացնում ենք ստացված հավասարման երկու կողմերը

n-րդ աստիճան:

;

Բ) հաշվի առնելով դա

, մենք ստանում ենք հավասարումը

f(x) = g (x);

)Մենք լուծում ենք հավասարումը և ստուգում ենք, քանի որ հավասարման երկու կողմերը հավասարաչափ բարձրացնելը կարող է հանգեցնել կողմնակի արմատների առաջացման: Այս ստուգումն իրականացվում է փոփոխականի հայտնաբերված արժեքները փոխարինելով սկզբնական հավասարման մեջ:

Հեղինակային իրավունք © 2005-2013 Xenoid v2.0

Կայքի նյութերի օգտագործումը հնարավոր է ակտիվ հղման դեպքում:

Մեզ համար կարևոր է ձեր գաղտնիության պահպանումը: Այդ իսկ պատճառով մենք մշակել ենք Գաղտնիության քաղաքականություն, որը նկարագրում է, թե ինչպես ենք մենք օգտագործում և պահպանում ձեր տվյալները: Խնդրում ենք վերանայել մեր գաղտնիության գործելակերպը և եթե հարցեր ունեք, տեղեկացրեք մեզ:

Անձնական տեղեկատվության հավաքագրում և օգտագործում

Անձնական տեղեկատվությունը վերաբերում է այն տվյալներին, որոնք կարող են օգտագործվել կոնկրետ անձի նույնականացման կամ կապ հաստատելու համար:

Ձեզանից կարող է պահանջվել տրամադրել ձեր անձնական տվյալները ցանկացած ժամանակ, երբ դուք կապվեք մեզ հետ:

Ստորև բերված են անձնական տեղեկատվության տեսակների մի քանի օրինակներ, որոնք մենք կարող ենք հավաքել և ինչպես կարող ենք օգտագործել այդպիսի տեղեկատվությունը:

Ինչ անձնական տվյալներ ենք մենք հավաքում.

• Երբ դուք դիմում եք ներկայացնում կայքում, մենք կարող ենք հավաքել տարբեր տեղեկություններ, ներառյալ ձեր անունը, հեռախոսահամարը, էլ.փոստի հասցեն և այլն:

Ինչպես ենք մենք օգտագործում ձեր անձնական տվյալները.

• Մեր հավաքած անձնական տեղեկությունները մեզ թույլ են տալիս կապ հաստատել ձեզ հետ եզակի առաջարկների, առաջխաղացումների և այլ իրադարձությունների և գալիք իրադարձությունների հետ:
• Ժամանակ առ ժամանակ մենք կարող ենք օգտագործել ձեր անձնական տվյալները կարևոր ծանուցումներ և հաղորդակցություններ ուղարկելու համար:
• Մենք կարող ենք նաև օգտագործել անձնական տվյալները ներքին նպատակների համար, ինչպիսիք են աուդիտի, տվյալների վերլուծության և տարբեր հետազոտությունների անցկացումը՝ մեր կողմից տրամադրվող ծառայությունները բարելավելու և ձեզ մեր ծառայությունների վերաբերյալ առաջարկություններ տրամադրելու համար:
• Եթե ​​դուք մասնակցում եք մրցանակների խաղարկության, մրցույթի կամ նմանատիպ ակցիայի, մենք կարող ենք օգտագործել ձեր տրամադրած տեղեկատվությունը նման ծրագրերը կառավարելու համար:

Տեղեկատվության բացահայտում երրորդ անձանց

Մենք ձեզանից ստացված տեղեկատվությունը երրորդ կողմերին չենք բացահայտում:

Բացառություններ.

• Անհրաժեշտության դեպքում՝ օրենքին համապատասխան, դատական ​​կարգով, դատական ​​գործընթացներում և/կամ Ռուսաստանի Դաշնության տարածքում պետական ​​մարմինների հրապարակային խնդրանքների կամ խնդրանքների հիման վրա՝ բացահայտել ձեր անձնական տվյալները: Մենք կարող ենք նաև բացահայտել ձեր մասին տեղեկությունները, եթե մենք որոշենք, որ նման բացահայտումն անհրաժեշտ է կամ տեղին է անվտանգության, օրենքի կիրառման կամ հանրային նշանակության այլ նպատակների համար:
• Վերակազմակերպման, միաձուլման կամ վաճառքի դեպքում մենք կարող ենք փոխանցել մեր հավաքած անձնական տվյալները համապատասխան իրավահաջորդ երրորդ կողմին:

Անձնական տեղեկատվության պաշտպանություն

Մենք նախազգուշական միջոցներ ենք ձեռնարկում, ներառյալ վարչական, տեխնիկական և ֆիզիկական, պաշտպանելու ձեր անձնական տվյալները կորստից, գողությունից և չարաշահումից, ինչպես նաև չարտոնված մուտքից, բացահայտումից, փոփոխությունից և ոչնչացումից:

Հարգելով ձեր գաղտնիությունը ընկերության մակարդակով

Ապահովելու համար, որ ձեր անձնական տվյալները անվտանգ են, մենք գաղտնիության և անվտանգության չափանիշները հաղորդում ենք մեր աշխատակիցներին և խստորեն կիրառում ենք գաղտնիության պրակտիկան:

Հանրահաշվական հավասարումների տեսակները և դրանց լուծման եղանակները

Մաթեմատիկայով հետաքրքրվող ուսանողների համար ավելի բարձր աստիճանի հանրահաշվական հավասարումներ լուծելիս արդյունավետ մեթոդ արմատները արագ գտնելու համար, մնացորդի հետ բաժանելով x -  երկանդամով կամ կացին + b-ով, Հորների սխեման է:

Դիտարկենք Հորների սխեման:

Նշենք թերի քանորդը P(x)-ի x – -ով բաժանելիս.

Q (x) = b 0 x n -1 + b 1 x n -2 + ... + b n -1, իսկ մնացորդը b n է:

Քանի որ P(x) = Q (x)(x–) + b n, ուրեմն հավասարությունը գործում է

ա 0 x n + а 1 x n -1 + … + а n = (b 0 x n -1 + b 1 x n -2 + … + b n -1)(х– ) + b n

Եկեք բացենք աջ կողմի փակագծերը և համեմատենք ձախ և աջ x-ի նույն հզորությունների գործակիցները։ Մենք ստանում ենք, որ a 0 = b 0, իսկ 1  k  n-ի համար գործում են a k = b k -  b k -1 հարաբերությունները: Հետևում է, որ b 0 = a 0 և b k = a k +  b k -1, 1  k  n:

Q (x) բազմանդամի գործակիցների և b n մնացորդի հաշվարկը գրում ենք աղյուսակի տեսքով.

ա 0

ա 1

ա 2

Ա n-1

Ա n

b 0 = a 0

b 1 = a 1 +  b 0

b 2 = a 2 +  b 1

b n-1 = a n-1 +  b n-2

b n = a n +  b n-1

Օրինակ 1. 2x 4 – 7x 3 – 3x 2 + 5x – 1 բազմանդամը բաժանեք x + 1-ի:

Լուծում. Մենք օգտագործում ենք Հորների սխեման:

2x 4 – 7x 3 – 3x 2 + 5x – 1-ը x + 1-ի բաժանելիս ստանում ենք 2x 3 – 9x 2 + 6x – 1

Պատասխան՝ 2 x 3 – 9x 2 + 6x – 1

Օրինակ 2. Հաշվեք P(3), որտեղ P(x) = 4x 5 – 7x 4 + 5x 3 – 2x + 1

Լուծում. Օգտագործելով Բեզութի թեորեմը և Հորների սխեման՝ մենք ստանում ենք.

Պատասխան՝ P(3) = 535

Զորավարժություններ

Օգտվելով Հորների գծապատկերից՝ բաժանիր բազմանդամը

4x 3 – x 5 + 132 – 8x 2 x + 2-ի վրա;

2) Բաժանեք բազմանդամը

2x 2 – 3x 3 – x + x 5 + 1 x + 1-ի վրա;

3) Գտե՛ք P 5 (x) = 2x 5 – 4x 4 – x 2 + 1 բազմանդամի արժեքը x = 7-ի համար:

1.1. Ամբողջ թվային գործակիցներով հավասարումների ռացիոնալ արմատների որոնում

Ամբողջ թվային գործակիցներով հանրահաշվական հավասարման ռացիոնալ արմատները գտնելու մեթոդը տրված է հետևյալ թեորեմով.

Թեորեմ.Եթե ​​ամբողջ գործակիցներով հավասարումն ունի ռացիոնալ արմատներ, ապա դրանք ազատ անդամի բաժանարարը առաջատար գործակցի բաժանարարի վրա բաժանելու գործակիցն են։

Ապացույց: a 0 x n + a 1 x n -1 + … + a n = 0

Թող x = p/ q-ն ռացիոնալ արմատ է, q-ն, p-ն համապարփակ են:

Փոխարինելով p/q կոտորակը հավասարման մեջ և ազատվելով հայտարարից՝ ստանում ենք.

ա 0 ռ n + a 1 p n -1 q + … + a n -1 pq n -1 + a n q n = 0 (1)

Եկեք վերաշարադրենք (1) երկու ձևով.

a n q n = р(– а 0 р n -1 – а 1 р n -2 q – … – а n -1 q n -1) (2)

ա 0 ռ n = q (– а 1 р n -1 –… – а n -1 рq n -2 – а n q n -1) (3)

(2) հավասարությունից հետևում է, որ a n q n-ը բաժանվում է p-ի, և քանի որ q n-ը և p-ն միաժամանակ պարզ են, ապա a n-ը բաժանվում է p-ի: Նմանապես, հավասարությունից (3) հետևում է, որ 0-ը բաժանվում է q-ի: Թեորեմն ապացուցված է.

Օրինակ 1. Լուծե՛ք 2x 3 – 7x 2 + 5x – 1 = 0 հավասարումը։

Լուծում. Հավասարումը չունի ամբողջ թվային արմատներ, մենք գտնում ենք հավասարման ռացիոնալ արմատները: Թող p /q անկրճատելի կոտորակը լինի հավասարման արմատը, ապա p-ն գտնվի ազատ անդամի բաժանարարների մեջ, այսինքն.  1 թվերի մեջ, իսկ q առաջատար գործակցի դրական բաժանարարների մեջ՝ 1; 2.

Նրանք. հավասարման ռացիոնալ արմատները պետք է փնտրել  1,  1/2 թվերի մեջ, նշանակել P 3 (x) = 2x 3 – 7x 2 + 5x – 1, P 3 (1)  0, P 3 (–1)  0,

P 3 (1/2) = 2/8 – 7/4 + 5/2 – 1 = 0, 1/2-ը հավասարման արմատն է։

2x 3 – 7x 2 + 5x – 1 = 2x 3 – x 2 – 6 x 2 + 3x + 2x – 1 = 0:

Մենք ստանում ենք. x 2 (2x – 1) – 3x (2x – 1)+ (2x – 1) = 0; (2x – 1) (x 2 – 3x + 1) = 0:

Երկրորդ գործոնը հավասարեցնելով զրոյի և լուծելով հավասարումը, ստանում ենք

Պատասխան.
,

Զորավարժություններ

Լուծել հավասարումներ.

6x 3 – 25x 2 + 3x + 4 = 0;

6x 4 – 7x 3 – 6x 2 + 2x + 1 = 0;

3x 4 – 8x 3 – 2x 2 + 7x – 1 = 0;

1.2. Փոխադարձ հավասարումներ և լուծման մեթոդներ

Սահմանում.Անհայտի նկատմամբ ամբողջ ուժերով հավասարումը կոչվում է փոխադարձ, եթե նրա գործակիցները, ձախ կողմի ծայրերից հավասար հեռավորության վրա, հավասար են միմյանց, այսինքն. ձևի հավասարումը

Ա x n + bx n -1 + cx n -2 + … + cx 2 + bx + a = 0

Կենտ աստիճանի փոխադարձ հավասարում

Ա x 2 n +1 + bx 2 n + cx 2 n -1 + … + cx 2 + bx + a = 0

միշտ արմատ ունի x = – 1: Հետևաբար, այն համարժեք է x + 1 = 0 և  x 2 n +  x 2 n -1 + … +  x +  = 0 հավասարումը միացնելուն: Վերջին հավասարումը a. զույգ աստիճանի փոխադարձ հավասարում. Այսպիսով, ցանկացած աստիճանի փոխադարձ հավասարումների լուծումը վերածվում է զույգ աստիճանի փոխադարձ հավասարումների լուծմանը:

Ինչպե՞ս լուծել այն: Թող տրվի զույգ աստիճանի փոխադարձ հավասարում

Ա x 2 n + bx 2 n -1 + … + dx n +1 + նախկին n + dx n -1 + … + bx + a = 0

Նկատի ունեցեք, որ x = 0 հավասարման արմատը չէ: Հետո հավասարումը բաժանում ենք x n-ի, ստանում ենք

Ա x n + bx n -1 + … + dx + e + dx -1 + … + bx 1- n + аx -n = 0

Ձախ կողմի տերմինները խմբավորում ենք զույգերով

Ա( x n + x - n ) + b (x n -1 + x -(n -1) + … + d(x + x -1) + e = 0

Մենք փոխարինում ենք x + x -1 = y: x 2 + x -2 = y 2 – 2 արտահայտությունները փոխարինելուց հետո;

x 3 + x -3 = y 3 – 3y; x 4 + x -4 = y 4 – 4y + 2 հավասարման մեջ մենք ստանում ենք հավասարումը ժամըАу n + Ըստ n -1 +Cy n -2 + … + Ey + D = 0:

Այս հավասարումը լուծելու համար հարկավոր է լուծել x + x -1 = y k ձևի մի քանի քառակուսային հավասարումներ, որտեղ k = 1, 2, ... n: Այսպիսով, մենք ստանում ենք սկզբնական հավասարման արմատները:

Օրինակ 1. Լուծե՛ք x 7 + x 6 – 5x 5 – 13x 4 – 13x 3 – 5x 2 + 2x + 1 = 0 հավասարումը:

Լուծում. x = – 1-ը հավասարման արմատն է: Եկեք կիրառենք Հորների սխեման։

Մեր հավասարումը կունենա հետևյալ ձևը.

(x + 1) (x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1) = 0

1) x + 1 = 0, x = -1;

2) x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1 = 0 | : x 3  0; x 3 + x 2 – 6x – 7 – 6/x + 1/x 2 + 1/x 3 =0:

Խմբավորելով՝ ստանում ենք.

Ներկայացնենք փոխարինում.
;
;
.

Համեմատաբար ստանում ենք ժամըհավասարումը՝ y 3 – 3y + y 2 – 2 – 6y – 7 = 0;

y 3 + y 2 – 9y – 9 = 0; y 2 (y + 1) - 9 (y + 1) = 0; (y + 1) (y 2 – 9); y 1 = -1, y 2,3 =  3:

Հավասարումների լուծում
,
,
,

մենք ստանում ենք արմատները.
,
,
,

Պատասխան՝ x 1 = -1,
,

Զորավարժություններ

Լուծել հավասարումներ.

2x 5 + 5x 4 – 13x 3 – 13x 2 + 5x + 2 = 0;

2x 4 + 3x 3 – 16x 2 + 3x + 2 = 0;

15x 5 + 34x 4 + 15x 3 – 15x 2 – 34x – 15 = 0:

1.3. Հավասարումների լուծման փոփոխական փոխարինման մեթոդ

Փոփոխական փոխարինման մեթոդը ամենատարածված մեթոդն է: Փոփոխական փոփոխություն կատարելու արվեստն այն է, որ տեսնենք, թե որ փոփոխությունն է առավել իմաստալից և ավելի արագ կբերի հաջողության:

Եթե ​​տրված է հավասարումը

F(f(x)) = 0, (1)

այնուհետև փոխարինելով y = f (x) անհայտը սկզբում այն ​​վերածվում է հավասարման

F(y) = 0, (2)

և այնուհետև (2) y 1, y 2, ..., y n, ... հավասարման բոլոր լուծումները գտնելուց հետո կրճատվում է f (x) = y 1, f (x) = y 2 հավասարումների բազմությունը լուծելու համար: ,..., f (x) = y 2,...

Փոփոխական փոխարինման մեթոդի իրականացման հիմնական ուղիներն են.

օգտագործելով կոտորակի հիմնական հատկությունը;

առանձնացնելով երկանդամի քառակուսին;

անցում դեպի հավասարումների համակարգ;

փակագծերի բացում զույգերով;

բացելով փակագծերը զույգերով և բաժանելով հավասարման երկու կողմերը.

հավասարման աստիճանի նվազում;

կրկնակի փոխարինում.

1.3.1. Հավասարման հզորության նվազեցում

Լուծեք հավասարումը (x 2 + x + 2) (x 2 + x + 3) = 6 (3)

Լուծում. Նշանակենք x 2 + x + 2 = y, ապա վերցնենք y (y + 1) = 6՝ լուծելով վերջինս՝ ստանում ենք y 1 = 2, y 2 = -3։ Այս հավասարումը (3) համարժեք է x 2 + x + 2 = 2 հավասարումների բազմությանը.

x 2 + x + 2 = -3

Լուծելով առաջինը՝ ստանում ենք x 1 = 0, x 2 = -1. Լուծելով երկրորդը՝ ստանում ենք
,

Պատասխան՝ x 1 = 0, x 2 = -1,

1.3.2. (x + a) (x +) ձևի չորրորդ աստիճանի հավասարումըբ )(x + գ )(x + դ ) = մ , որտեղ a + b = c + d, կամ a + c = b + d, կամ a + d = b + c.

Օրինակ. Լուծեք (x - 1) (x - 7) (x -4) (x + 2) = 40 հավասարումը

Լուծում. – 1- 4 = - 7 + 2, - 5 = - 5, բազմապատկելով այս զույգ փակագծերը, ստանում ենք հավասարումը (x 2 - 5x - 14)(x 2 - 5x + 4) = 40

Ներկայացնենք փոխարինումը` x 2 - 5x – 14 = y, ստանում ենք y(y + 18) = 40, y 2 + 18y = 40, y 2 + 18y – 40 = 0. y 1 = -20, y հավասարումը: 2 = 2. Վերադառնալով սկզբնական փոփոխականին՝ լուծում ենք հավասարումների մի շարք.

X 2 - 5x – 14 = - 20 x 1 = 2; x 2 = 3

x 2 - 5x – 14 = 2 x 3.4 =

Պատասխան՝ x 1 = 2; x 2 = 3 x 3.4 =

1.3.3. Ձևի հավասարումը (x + a) (x + b) (x + c) (x + d) = Ex 2,

Որտեղ ab = cd, կամ ac =bd, կամ ad = bc: Բացեք փակագծերը զույգերով և երկու մասերը բաժանեք x 2  0-ի:

Օրինակ. (x - 1) (x - 2) (x - 8) (x - 4) = 4x 2

Լուծում. Առաջին և երրորդ և երկրորդ և չորրորդ փակագծերի թվերի արտադրյալը հավասար են, այսինքն. – 8 (- 1) = (- 2)(- 4). Բազմապատկենք նշված զույգ փակագծերը և գրենք (x 2 - 9x + 8) (x 2 - 6x + 8) = 4x 2 հավասարումը։

Քանի որ x = 0 հավասարման արմատը չէ, մենք հավասարման երկու կողմերը բաժանում ենք x-ի 2  0, մենք ստանում ենք.
, փոխարինում:
, սկզբնական հավասարումը կունենա հետևյալ ձևը.տ(տ+3) =4, տ 2 + 3 տ=4, տ 2 + 3 տ – 4=0, տ 1 =1, տ 2 = - 4.

Եկեք վերադառնանք սկզբնական փոփոխականին.

x 2 - 10x + 8 = 0

x 2 - 5x + 8 = 0

Լուծում ենք առաջին հավասարումը, ստանում ենք x 1,2 = 5 

Երկրորդ հավասարումը արմատներ չունի։

Պատասխան՝ x 1,2 = 5 

1.3.4. Չորրորդ տիպի հավասարում (ax 2 + b 1 x + c) (a x 2 + b 2 x + c) = A x 2

Հավասարում (կացին 2 + բ 1 x+ գ)(ա x 2 + բ 2 x + գ) = Ա x 2, որտեղ ք  0, Ա  2
, որը անհայտը փոխարինելուց հետո
կարող է վերագրվել որպես քառակուսի և կարող է հեշտությամբ լուծվել:

Օրինակ. (x 2 + x+ 2) (x 2 + 2x + 2) = 2x 2

Լուծում. Հեշտ է տեսնել, որ x = 0-ը այս հավասարման արմատը չէ՝ այս հավասարումը x-ով բաժանելով 2 , մենք ստանում ենք հավասարումը

փոխարինում
, ստանում ենք (y+1)(y+2) = 2 հավասարումը, լուծելով այն՝ ունենք y արմատներ. 1 = 0; ժամը 2-ին = - 3, հետևաբար սկզբնական հավասարումը համարժեք է հավասարումների բազմությանը

լուծելով, մենք ստանում ենք x 1 = -1; x 2 = -2.

Պատասխան՝ x 1 = -1; x 2 = -2

1.3.5. Ձևի հավասարումը. a (cx 2 + p 1 x + q) 2 + b (cx 2 + p 2 x + q) 2 = Ax 2

Հավասարումը ա(cx 2 + էջ 1 x + ք) 2 + բ(cx 2 + էջ 2 x + ք) 2 = Կացին 2 որտեղ ա, բ, գ, ք, Աայնպիսին են, որ ք 0, Ա 0, գ 0, ա 0, բ 0-ն արմատ չունի x = 0, ուստի հավասարումը բաժանելով x-ի 2 , ստանում ենք համարժեք հավասարում
, որը փոխարինելուց հետո
կարելի է վերաշարադրել որպես քառակուսի հավասարում, որը կարելի է հեշտությամբ լուծել: + 1)( x 2 – 14x + 15 = 0

x 2 – 7 x + 15 = 0

Պատասխան.

Ֆիզիկայի որոշ խնդիրներում հնարավոր չէ ուղիղ կապ հաստատել գործընթացը նկարագրող մեծությունների միջև։ Բայց կարելի է ստանալ ուսումնասիրվող ֆունկցիաների ածանցյալները պարունակող հավասարություն։ Ահա թե ինչպես են առաջանում դիֆերենցիալ հավասարումները և դրանց լուծման անհրաժեշտությունը՝ անհայտ ֆունկցիա գտնելու համար։

Այս հոդվածը նախատեսված է նրանց համար, ովքեր բախվում են դիֆերենցիալ հավասարման լուծման խնդրին, որտեղ անհայտ ֆունկցիան մեկ փոփոխականի ֆունկցիա է։ Տեսությունը կառուցված է այնպես, որ դիֆերենցիալ հավասարումների զրոյական իմացությամբ դուք կարող եք հաղթահարել ձեր խնդիրը:

Դիֆերենցիալ հավասարումների յուրաքանչյուր տեսակ կապված է լուծման մեթոդի հետ՝ մանրամասն բացատրություններով և բնորոշ օրինակների և խնդիրների լուծումներով: Ձեզ մնում է միայն որոշել ձեր խնդրի դիֆերենցիալ հավասարման տեսակը, գտնել նմանատիպ վերլուծված օրինակ և կատարել նմանատիպ գործողություններ:

Դիֆերենցիալ հավասարումները հաջողությամբ լուծելու համար ձեզ անհրաժեշտ կլինի նաև տարբեր ֆունկցիաների հակաածանցյալների բազմություններ (անորոշ ինտեգրալներ) գտնելու ունակություն: Անհրաժեշտության դեպքում խորհուրդ ենք տալիս անդրադառնալ բաժնին:

Նախ, մենք կդիտարկենք առաջին կարգի սովորական դիֆերենցիալ հավասարումների տեսակները, որոնք կարող են լուծվել ածանցյալի նկատմամբ, այնուհետև կանցնենք երկրորդ կարգի ODE-ներին, այնուհետև կանդրադառնանք ավելի բարձր կարգի հավասարումների և կավարտենք համակարգերով. դիֆերենցիալ հավասարումներ.

Հիշենք, որ եթե y-ն x արգումենտի ֆունկցիա է:

Առաջին կարգի դիֆերենցիալ հավասարումներ.

Ձևի առաջին կարգի ամենապարզ դիֆերենցիալ հավասարումները.

Եկեք գրենք նման հեռակառավարման մի քանի օրինակ .

Դիֆերենցիալ հավասարումներ կարելի է լուծել ածանցյալի նկատմամբ՝ հավասարության երկու կողմերը բաժանելով f(x)-ի: Այս դեպքում մենք հասնում ենք մի հավասարման, որը համարժեք կլինի սկզբնականին f(x) ≠ 0-ի համար։ Նման ODE-ների օրինակներ են.

Եթե ​​կան x փաստարկի արժեքներ, որոնց դեպքում f(x) և g(x) ֆունկցիաները միաժամանակ անհետանում են, ապա հայտնվում են լրացուցիչ լուծումներ: Հավասարման լրացուցիչ լուծումներ տրված x-ը այս արգումենտի արժեքների համար սահմանված ցանկացած ֆունկցիա է: Նման դիֆերենցիալ հավասարումների օրինակները ներառում են.

Երկրորդ կարգի դիֆերենցիալ հավասարումներ.

Երկրորդ կարգի գծային միատարր դիֆերենցիալ հավասարումներ՝ հաստատուն գործակիցներով.

Մշտական ​​գործակիցներով LDE-ն դիֆերենցիալ հավասարումների շատ տարածված տեսակ է: Դրանց լուծումն առանձնապես դժվար չէ։ Նախ՝ հայտնաբերվում են բնորոշ հավասարման արմատները . Տարբեր p-ի և q-ի համար հնարավոր է երեք դեպք. բնորոշ հավասարման արմատները կարող են լինել իրական և տարբեր, իրական և համընկնող: կամ բարդ կոնյուգատներ: Կախված բնութագրիչ հավասարման արմատների արժեքներից, դիֆերենցիալ հավասարման ընդհանուր լուծումը գրվում է հետևյալ կերպ. , կամ , կամ համապատասխանաբար։

Օրինակ, դիտարկենք գծային միատարր երկրորդ կարգի դիֆերենցիալ հավասարումը հաստատուն գործակիցներով: Նրա բնորոշ հավասարման արմատներն են k 1 = -3 և k 2 = 0: Արմատները իրական են և տարբեր, հետևաբար հաստատուն գործակիցներով LODE-ի ընդհանուր լուծումն ունի ձև


Երկրորդ կարգի գծային անհամասեռ դիֆերենցիալ հավասարումներ՝ հաստատուն գործակիցներով.

y հաստատուն գործակիցներով երկրորդ կարգի LDDE-ի ընդհանուր լուծումը որոնվում է համապատասխան LDDE-ի ընդհանուր լուծման գումարի տեսքով. և սկզբնական անհամասեռ հավասարման որոշակի լուծում, այսինքն՝ . Նախորդ պարբերությունը նվիրված է հաստատուն գործակիցներով համասեռ դիֆերենցիալ հավասարման ընդհանուր լուծում գտնելուն: Իսկ կոնկրետ լուծումը որոշվում է կա՛մ սկզբնական հավասարման աջ կողմում գտնվող f(x) ֆունկցիայի որոշակի ձևի համար անորոշ գործակիցների մեթոդով, կա՛մ կամայական հաստատունների փոփոխման մեթոդով։

Որպես հաստատուն գործակիցներով երկրորդ կարգի LDDE-ների օրինակներ՝ մենք տալիս ենք


Տեսությունը հասկանալու և օրինակների մանրամասն լուծումներին ծանոթանալու համար էջում առաջարկում ենք գծային անհամասեռ երկրորդ կարգի դիֆերենցիալ հավասարումներ՝ հաստատուն գործակիցներով։

Գծային միատարր դիֆերենցիալ հավասարումներ (LODE) և երկրորդ կարգի գծային անհամասեռ դիֆերենցիալ հավասարումներ (LNDEs):

Այս տեսակի դիֆերենցիալ հավասարումների հատուկ դեպք են LODE և LDDE հաստատուն գործակիցներով:

LODE-ի ընդհանուր լուծումը որոշակի հատվածի վրա ներկայացված է այս հավասարման y 1 և y 2 գծային անկախ մասնակի լուծումների գծային համադրությամբ, այսինքն. .

Հիմնական դժվարությունը հենց այս տեսակի դիֆերենցիալ հավասարման գծային անկախ մասնակի լուծումներ գտնելն է: Սովորաբար, կոնկրետ լուծումներն ընտրվում են գծային անկախ ֆունկցիաների հետևյալ համակարգերից.


Այնուամենայնիվ, կոնկրետ լուծումները միշտ չէ, որ ներկայացված են այս ձևով:

LOD-ի օրինակ է .

LDDE-ի ընդհանուր լուծումը որոնվում է ձևով, որտեղ գտնվում է համապատասխան LDDE-ի ընդհանուր լուծումը և հանդիսանում է սկզբնական դիֆերենցիալ հավասարման որոշակի լուծում: Մենք պարզապես խոսեցինք այն գտնելու մասին, բայց այն կարելի է որոշել՝ օգտագործելով կամայական հաստատունների փոփոխման մեթոդը:

LNDU-ի օրինակ կարելի է բերել .

Բարձրագույն կարգերի դիֆերենցիալ հավասարումներ.

Դիֆերենցիալ հավասարումներ, որոնք թույլ են տալիս կրճատել հերթականությամբ:

Դիֆերենցիալ հավասարման կարգը , որը չի պարունակում ցանկալի ֆունկցիան և դրա ածանցյալները մինչև k-1 կարգը, կարող է կրճատվել մինչև n-k՝ փոխարինելով .

Այս դեպքում սկզբնական դիֆերենցիալ հավասարումը կկրճատվի մինչև . Նրա p(x) լուծումը գտնելուց հետո մնում է վերադառնալ փոխարինողին և որոշել y անհայտ ֆունկցիան։

Օրինակ՝ դիֆերենցիալ հավասարումը փոխարինումից հետո այն կդառնա բաժանելի փոփոխականներով հավասարում, և դրա կարգը կնվազի երրորդից առաջինը: