Qual è la somma degli angoli? Teorema sulla somma degli angoli di un triangolo. Tipi per dimensione dell'angolo

Somma degli angoli del triangolo- importante, ma sufficiente tema semplice, che viene insegnato in geometria di 7a elementare. L'argomento consiste in un teorema, una breve dimostrazione e diverse conseguenze logiche. La conoscenza di questo argomento aiuta a risolverlo problemi geometrici durante il successivo studio dell’argomento.

Teorema: quali sono gli angoli di un triangolo arbitrario sommati?

Il teorema afferma che se prendiamo un triangolo qualsiasi, indipendentemente dal suo tipo, la somma di tutti gli angoli sarà invariabilmente 180 gradi. Ciò è dimostrato come segue:

• ad esempio, preso il triangolo ABC, tracciamo una retta passante per il punto B situato al vertice e designiamola come “a”, la retta “a” è strettamente parallela al lato AC;
• tra la retta “a” ed i lati AB e BC si designano gli angoli, contrassegnandoli con i numeri 1 e 2;
• l'angolo 1 è considerato uguale all'angolo A e l'angolo 2 è considerato uguale all'angolo C, poiché questi angoli sono considerati trasversali;
• quindi, la somma tra gli angoli 1, 2 e 3 (che è designato al posto dell'angolo B) è riconosciuta come uguale all'angolo spiegato con il vertice B - ed è 180 gradi.

Se la somma degli angoli indicati dai numeri è 180 gradi, allora la somma degli angoli A, B e C viene riconosciuta pari a 180 gradi. Questa regola è vera per qualsiasi triangolo.

Ciò che segue dal teorema geometrico

È consuetudine evidenziare alcuni corollari del teorema precedente.

• Se il problema considera un triangolo con un angolo retto, per impostazione predefinita uno dei suoi angoli sarà uguale a 90 gradi e anche la somma degli angoli acuti sarà di 90 gradi.
• Se stiamo parlando di un triangolo isoscele rettangolo, i suoi angoli acuti, la cui somma è di 90 gradi, saranno individualmente pari a 45 gradi.
• Un triangolo equilatero è composto da tre angoli uguali, rispettivamente, ciascuno di essi sarà pari a 60 gradi e in totale saranno 180 gradi.
• L'angolo esterno di ogni triangolo sarà uguale alla somma di due angoli interni non adiacenti ad esso.

Si può ricavare la seguente regola: ogni triangolo ha almeno due angoli acuti. In alcuni casi, un triangolo è costituito da tre angoli acuti e, se ce ne sono solo due, il terzo angolo sarà ottuso o retto.

Teorema. La somma degli angoli interni di un triangolo è uguale a due angoli retti.

Prendiamo un triangolo ABC (Fig. 208). Indichiamo i suoi angoli interni con i numeri 1, 2 e 3. Dimostriamolo

∠1 + ∠2 + ∠3 = 180°.

Tracciamo per qualche vertice del triangolo, ad esempio B, una linea retta MN parallela ad AC.

Al vertice B abbiamo tre angoli: ∠4, ∠2 e ∠5. La loro somma è un angolo retto, quindi è pari a 180°:

∠4 + ∠2 + ∠5 = 180°.

Ma ∠4 = ∠1 sono angoli trasversali interni con rette parallele MN e AC e secanti AB.

∠5 = ∠3 - questi sono angoli trasversali interni con linee parallele MN e AC e secanti BC.

Ciò significa che ∠4 e ∠5 possono essere sostituiti dai loro uguali ∠1 e ∠3.

Pertanto, ∠1 + ∠2 + ∠3 = 180°. Il teorema è stato dimostrato.

2. Proprietà dell'angolo esterno di un triangolo.

Infatti, nel triangolo ABC (Fig. 209) ∠1 + ∠2 = 180° - ∠3, ma anche ∠ВСD, anche l'angolo esterno di questo triangolo, non adiacente a ∠1 e ∠2, è pari a 180° - ∠3 .

Così:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Pertanto, ∠1 + ∠2= ∠BCD.

La proprietà derivata dell'angolo esterno di un triangolo chiarisce il contenuto del teorema precedentemente dimostrato sull'angolo esterno di un triangolo, il quale affermava soltanto che l'angolo esterno di un triangolo è maggiore di ciascun angolo interno di un triangolo non adiacente ad esso; ora è stabilito che l'angolo esterno è uguale alla somma di entrambi gli angoli interni non adiacenti ad esso.

3. Proprietà di un triangolo rettangolo con un angolo di 30°.

Sia l'angolo B del triangolo rettangolo ACB uguale a 30° (fig. 210). Allora il suo altro angolo acuto sarà pari a 60°.

Dimostriamo che il cateto AC è uguale alla metà dell'ipotenusa AB. Allunghiamo la gamba AC oltre il vertice dell'angolo retto C e mettiamo da parte un segmento CM uguale al segmento AC. Colleghiamo il punto M al punto B. Il triangolo risultante ВСМ è uguale al triangolo ACB. Vediamo che ogni angolo del triangolo ABM è uguale a 60°, quindi questo triangolo è un triangolo equilatero.

Il cateto AC è uguale alla metà di AM, e poiché AM è uguale ad AB, il cateto AC sarà uguale alla metà dell'ipotenusa AB.

La somma degli angoli interni di un triangolo è 180 0. Questo è uno degli assiomi fondamentali della geometria di Euclide. Questa è la geometria che studiano gli scolari. La geometria è definita come la scienza che studia le forme spaziali del mondo reale.

Cosa spinse gli antichi greci a sviluppare la geometria? La necessità di misurare campi, prati - aree della superficie terrestre. Allo stesso tempo, gli antichi greci accettavano che la superficie della Terra fosse orizzontale e piatta. Tenendo conto di questo presupposto, furono creati gli assiomi di Euclide, inclusa la somma degli angoli interni di un triangolo di 180 0.

Un assioma è una proposizione che non richiede prova. Come dovrebbe essere inteso? Viene espresso un desiderio adatto alla persona e poi viene confermato da illustrazioni. Ma tutto ciò che non è dimostrato è finzione, qualcosa che nella realtà non esiste.

Prendendo la superficie terrestre in orizzontale, gli antichi greci accettavano automaticamente la forma della Terra come piatta, ma è diversa: sferica. In natura non esistono piani orizzontali o linee rette, perché la gravità piega lo spazio. Linee rette e piani orizzontali si trovano solo nel cervello umano.

Pertanto, la geometria di Euclide, che spiega le forme spaziali del mondo immaginario, è un simulacro, una copia che non ha originale.

Uno degli assiomi di Euclide afferma che la somma degli angoli interni di un triangolo è 180°. Infatti, nello spazio curvo reale, ovvero sulla superficie sferica della Terra, la somma degli angoli interni di un triangolo è sempre maggiore di 180 0.

Pensiamo così. Qualsiasi meridiano del globo si interseca con l'equatore con un angolo di 90°. Per ottenere un triangolo, devi allontanare un altro meridiano dal meridiano. La somma degli angoli del triangolo compreso tra i meridiani e il lato dell'equatore sarà 180 0. Ma ci sarà ancora un angolo al polo. Di conseguenza, la somma di tutti gli angoli sarà maggiore di 180 0.

Se i lati si intersecano con un angolo di 90 0 al polo, la somma degli angoli interni di tale triangolo sarà 270 0. Due meridiani che intersecano l'equatore ad angolo retto in questo triangolo saranno paralleli tra loro, e al polo che si intersecano con un angolo di 90 0 diventeranno perpendicolari. Si scopre che due linee parallele sullo stesso piano non solo si intersecano, ma possono anche essere perpendicolari al polo.

Naturalmente, i lati di un tale triangolo non saranno linee rette, ma convesse, ripetendo la forma sferica globo. Ma questo è esattamente il mondo reale dello spazio.

La geometria dello spazio reale, tenendo conto della sua curvatura a metà del XIX secolo. sviluppato dal matematico tedesco B. Riemann (1820-1866). Ma questo non viene detto agli scolari.

Quindi la geometria euclidea, che assume la forma della Terra come piatta con una superficie orizzontale, cosa che in realtà non è, è un simulacro. La nootica è la geometria riemanniana che tiene conto della curvatura dello spazio. La somma degli angoli interni del triangolo è maggiore di 180 0.

Prova

Permettere ABC" - triangolo arbitrario. Conduciamoci dall'alto B linea parallela alla linea AC. (tale linea retta è chiamata linea retta euclidea). Segniamo un punto su questo D in modo che i punti UN E D giacere su lati opposti di una linea retta AVANTI CRISTO..Angoli DBC E ACB uguale come giacitura trasversale interna formata da una secante AVANTI CRISTO. con linee parallele AC. E B.D. Pertanto, la somma degli angoli di un triangolo ai vertici B E CON uguale all'angolo ABD.La somma di tutti e tre gli angoli di un triangolo è uguale alla somma degli angoli ABD E BAC. Poiché questi angoli sono interni unilaterali per paralleli AC. E B.D alla secante AB, allora la loro somma è 180°. Il teorema è stato dimostrato.

Conseguenze

Dal teorema segue che ogni triangolo ha due angoli acuti. Infatti, usando la dimostrazione per assurdo, supponiamo che il triangolo abbia un solo angolo acuto o nessun angolo acuto. Allora questo triangolo ha almeno due angoli, ciascuno dei quali è almeno di 90°. La somma di questi angoli non è inferiore a 180°. Ma questo è impossibile, poiché la somma di tutti gli angoli di un triangolo è 180°. Q.E.D.

Generalizzazione nella teoria del simplesso

Dov'è l'angolo tra le facce i e j del simplesso.

Appunti

• Su una sfera la somma degli angoli di un triangolo supera sempre i 180°, la differenza si chiama eccesso sferico ed è proporzionale all'area del triangolo.
• Nel piano Lobachevskij la somma degli angoli di un triangolo è sempre minore di 180°. La differenza è anche proporzionale all'area del triangolo.

Guarda anche

Fondazione Wikimedia. 2010.

Scopri cos'è il "Teorema della somma degli angoli di un triangolo" in altri dizionari:

Proprietà dei poligoni nella geometria euclidea: la somma degli angoli n di un triangolo è 180°(n 2). Indice 1 Prova 2 Nota ... Wikipedia

Il teorema di Pitagora è uno dei teoremi fondamentali della geometria euclidea, che stabilisce la relazione tra i lati di un triangolo rettangolo. Indice 1 ...Wikipedia

Il teorema di Pitagora è uno dei teoremi fondamentali della geometria euclidea, che stabilisce la relazione tra i lati di un triangolo rettangolo. Indice 1 Affermazioni 2 Prove ... Wikipedia

Il teorema del coseno è una generalizzazione del teorema di Pitagora. Il quadrato di un lato di un triangolo è uguale alla somma dei quadrati degli altri due lati senza il doppio del prodotto di questi lati per il coseno dell'angolo compreso tra loro. Per un triangolo piano con lati a,b,c e l'angolo α... ... Wikipedia

Questo termine ha altri significati, vedi Triangolo (significati). Un triangolo (nello spazio euclideo) lo è figura geometrica, formato da tre segmenti che collegano tre punti che non giacciono sulla stessa retta. Tre punti,... ... Wikipedia

Notazione standard Un triangolo è il poligono più semplice avente 3 vertici (angoli) e 3 lati; parte del piano delimitata da tre punti che non giacciono sulla stessa linea e da tre segmenti che collegano questi punti a coppie. Vertici di un triangolo ... Wikipedia

Matematico greco antico. Lavorò ad Alessandria nel III secolo. AVANTI CRISTO e. L'opera principale “Principia” (15 libri), contenente i fondamenti della matematica antica, della geometria elementare, della teoria dei numeri, teoria generale relazioni e metodi per determinare aree e volumi,... ... Dizionario enciclopedico

- (morto tra il 275 e il 270 a.C.) matematico greco antico. Non ci sono pervenute informazioni sull'ora e sul luogo della sua nascita, ma è noto che Euclide visse ad Alessandria e il periodo di massimo splendore della sua attività avvenne durante il regno di Tolomeo I in Egitto... ... Grande dizionario enciclopedico

Geometria simile alla geometria euclidea in quanto definisce il movimento delle figure, ma differisce dalla geometria euclidea in quanto uno dei suoi cinque postulati (il secondo o il quinto) è sostituito dalla sua negazione. Negazione di uno dei postulati euclidei... ... Enciclopedia di Collier

Triangolo . Triangolo acuto, ottuso e rettangolo.

Gamba e ipotenusa. Triangolo isoscele e equilatero.

Somma degli angoli di un triangolo.

Angolo esterno di un triangolo. Segni di uguaglianza dei triangoli.

Linee e punti notevoli in un triangolo: altezze, mediane,

bisettrici, mediana e perpendicolari, ortocentro,

centro di gravità, centro di un cerchio circoscritto, centro di un cerchio inscritto.

Teorema di Pitagora. Proporzioni in un triangolo arbitrario.

Triangolo è un poligono con tre lati (o tre angoli). I lati di un triangolo sono spesso indicati da lettere minuscole che corrispondono alle lettere maiuscole che rappresentano i vertici opposti.

Se tutti e tre gli angoli sono acuti (Fig. 20), allora questo triangolo acuto . Se uno degli angoli è giusto(C, Fig.21), questo è triangolo rettangolo; latiun, bsi chiamano formanti un angolo retto gambe; latoCopposto si chiama l'angolo retto ipotenusa. Se uno di angoli ottusi (B, Fig. 22), questo è triangolo ottuso.


Triangolo ABC (Fig. 23) - isoscele, Se due i suoi lati sono uguali (UN= C); vengono chiamati questi lati uguali laterale, viene chiamata la terza parte base triangolo. Triangolo ABC (Fig. 24) – equilatero, Se Tutto i suoi lati sono uguali (UN = B = C). Generalmente ( UN ≠ B ≠ C) abbiamo scaleno triangolo .

Proprietà fondamentali dei triangoli. In qualsiasi triangolo:

1. Di fronte al lato maggiore si trova l'angolo maggiore e viceversa.

2. Angoli uguali giacciono opposti a lati uguali e viceversa.

In particolare, tutti gli angoli dentro equilatero triangolo sono uguali.

3. La somma degli angoli di un triangolo è 180 º .

Dalle ultime due proprietà segue che ogni angolo è equilatero

il triangolo è 60 º.

4. Proseguendo uno dei lati del triangolo (AC, Fig. 25), noi abbiamo esterno

angolo BCD . L'angolo esterno di un triangolo è uguale alla somma degli angoli interni,

non adiacente ad esso : BCD = A + B.

5. Qualunque il lato di un triangolo è minore della somma degli altri due lati e maggiore

le loro differenze (UN < B + C, UN > B – C;B < UN + C, B > UN – C;C < UN + B,C > UN – B).

Segni di uguaglianza dei triangoli.

I triangoli sono congruenti se sono rispettivamente uguali:

UN ) due lati e l'angolo compreso tra loro;

B ) due angoli e il lato ad essi adiacente;

c) tre lati.

Segni di uguaglianza dei triangoli rettangoli.

Due rettangolare i triangoli sono uguali se è soddisfatta una delle seguenti condizioni:

1) le loro gambe sono uguali;

2) il cateto e l'ipotenusa di un triangolo sono uguali al cateto e all'ipotenusa dell'altro;

3) l'ipotenusa e l'angolo acuto di un triangolo sono uguali all'ipotenusa e all'angolo acuto dell'altro;

4) il cateto e l'angolo acuto adiacente di un triangolo sono uguali al cateto e l'angolo acuto adiacente dell'altro;

5) la gamba e l'angolo acuto opposto di un triangolo sono uguali alla gamba e l'angolo acuto opposto dell'altro.

Linee e punti meravigliosi nel triangolo.

Altezza il triangolo èperpendicolare,abbassato da qualsiasi vertice al lato opposto ( o la sua continuazione). Questo lato è chiamatobase del triangolo . Le tre altezze di un triangolo si intersecano semprea un certo punto, chiamato ortocentro triangolo. Ortocentro di un triangolo acuto (punto O , Fig. 26) si trova all'interno del triangolo, eortocentro di un triangolo ottuso (punto O , fig.27) – al di fuori; L'ortocentro di un triangolo rettangolo coincide con il vertice dell'angolo retto.

Mediano - Questo segmento , che collega qualsiasi vertice di un triangolo al centro del lato opposto. Tre mediane di un triangolo (AD, BE, CF, fig.28) si intersecano in un punto O , sempre all'interno del triangolo ed essere suo centro di gravità. Questo punto divide ciascuna mediana in un rapporto di 2:1, contando dal vertice.

Bisettrice - Questo segmento bisettore angolo dal vertice al punto intersezioni con il lato opposto. Tre bisettrici di un triangolo (AD, BE, CF, fig.29) si intersecano in un punto Oh, sempre sdraiato all'interno del triangolo E essendo centro del cerchio inscritto(vedi sezione “Iscrittoe poligoni circoscritti").

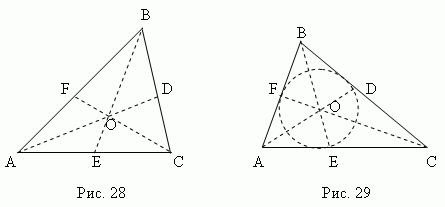
La bisettrice divide il lato opposto in parti proporzionali ai lati adiacenti ; ad esempio, nella Fig. 29 AE: CE = AB: BC.

Perpendicolare mediana è una perpendicolare tracciata dal centro punti del segmento (lati). Tre bisettrici perpendicolari del triangolo ABC(KO, MO, NO, fig. 30 ) si intersecano in un punto O, che è centro cerchio circoscritto (punti K, M, N – i punti medi dei lati del triangolo ABC).

In un triangolo acutangolo questo punto si trova all'interno del triangolo; in ottuso - fuori; in un rettangolare - nel mezzo dell'ipotenusa. Ortocentro, baricentro, circocentro e cerchio inscritto coincidono solo in un triangolo equilatero.

Teorema di Pitagora. In un triangolo rettangolo, il quadrato della lunghezzaL'ipotenusa è uguale alla somma dei quadrati delle lunghezze dei cateti.

La dimostrazione del teorema di Pitagora segue chiaramente dalla Fig. 31. Considera un triangolo rettangolo ABC con le gambe un, b e ipotenusa C.

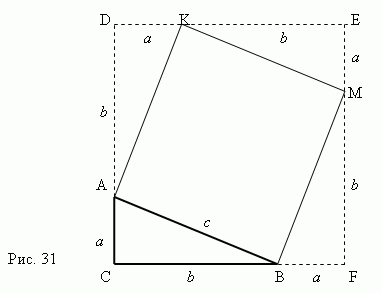
Costruiamo un quadrato AKMB utilizzando l'ipotenusa AB come lato. Poicontinuare i lati del triangolo rettangolo ABC in modo da ottenere un quadrato CDEF , il cui lato è ugualea+b.Ora è chiaro che l'area della piazza CDEF è uguale a ( a+b) 2 . D'altra parte, questo l'area è uguale alla somma le zone quattro triangoli rettangoli e il quadrato AKMB, cioè

C 2 + 4 (ab / 2) = C 2 + 2 ab,

da qui,

C 2 + 2 ab= (a+b) 2 ,

e infine abbiamo:

C 2 =UN 2 +b 2 .

Proporzioni in un triangolo arbitrario.

Nel caso generale (per un triangolo arbitrario) abbiamo:

C 2 =UN 2 +b 2 – 2ab· cos C,

dove C – angolo tra i latiUN E B .