Come determinare il segno della proiezione su un asse. Formule di base per trovare le distanze utilizzando la proiezione di un vettore su un asse. Prodotto vettoriale di vettori di coordinate

§ 3. Proiezioni di un vettore sugli assi coordinati

1. Trovare le proiezioni geometricamente.

Vettore
- proiezione del vettore sull'asse BUE
- proiezione del vettore sull'asse OH

Definizione 1. Proiezione vettoriale su qualsiasi asse delle coordinate c'è un numero preso con un segno più o meno, corrispondente alla lunghezza del segmento situato tra le basi delle perpendicolari cadute dall'inizio e dalla fine del vettore all'asse delle coordinate.

Il segno di proiezione è definito come segue. Se, quando ci si sposta lungo l'asse delle coordinate, si verifica un movimento dal punto di proiezione dell'inizio del vettore al punto di proiezione della fine del vettore nella direzione positiva dell'asse, la proiezione del vettore è considerata positiva . Se è opposto all'asse, la proiezione è considerata negativa.

La figura mostra che se il vettore è orientato in qualche modo opposto all'asse delle coordinate, la sua proiezione su questo asse è negativa. Se un vettore è orientato in qualche modo nella direzione positiva dell'asse delle coordinate, allora la sua proiezione su questo asse è positiva.

Se un vettore è perpendicolare all'asse delle coordinate, la sua proiezione su questo asse è zero.
Se un vettore è codirezionale con un asse, la sua proiezione su questo asse è uguale al valore assoluto del vettore.
Se un vettore è diretto in modo opposto all'asse delle coordinate, la sua proiezione su questo asse è uguale in valore assoluto al valore assoluto del vettore preso con un segno meno.

2. La maggior parte definizione generale proiezioni.

Da un triangolo rettangolo ABD: .

Definizione 2. Proiezione vettoriale su qualsiasi asse delle coordinate c'è un numero pari al prodotto del modulo del vettore e del coseno dell'angolo formato dal vettore con la direzione positiva dell'asse delle coordinate.

Il segno della proiezione è determinato dal segno del coseno dell'angolo formato dal vettore con la direzione positiva dell'asse.
Se l'angolo è acuto, allora il coseno ha segno positivo e le proiezioni sono positive. Per gli angoli ottusi il coseno ha segno negativo, quindi in questi casi le proiezioni sull'asse sono negative.
- quindi, per i vettori perpendicolari all'asse, la proiezione è zero.

In fisica per il grado 9 (I.K.Kikoin, A.K.Kikoin, 1999),
compito №5
al capitolo " CAPITOLO 1. INFORMAZIONI GENERALI SUL TRAFFICO».

1. Cos'è chiamata proiezione di un vettore sull'asse delle coordinate?

1. La proiezione del vettore a sull'asse delle coordinate è la lunghezza del segmento tra le proiezioni dell'inizio e della fine del vettore a (perpendicolari lasciate cadere da questi punti sull'asse) su questo asse delle coordinate.

2. In che modo il vettore spostamento di un corpo è correlato alle sue coordinate?

2. Le proiezioni del vettore spostamento s sugli assi delle coordinate sono uguali alla variazione delle coordinate del corpo corrispondente.

3. Se la coordinata di un punto aumenta nel tempo, quale segno ha la proiezione del vettore spostamento sull'asse delle coordinate? E se diminuisse?

3. Se la coordinata di un punto aumenta nel tempo, la proiezione del vettore spostamento sull'asse delle coordinate sarà positiva, perché in questo caso si passerà dalla proiezione dell'inizio alla proiezione della fine del vettore nella direzione dell'asse stesso.

Se la coordinata di un punto diminuisce nel tempo, la proiezione del vettore spostamento sull'asse delle coordinate sarà negativa, perché in questo caso si passerà dalla proiezione dell'inizio alla proiezione della fine del vettore contro la guida dell'asse stesso.

4. Se il vettore spostamento è parallelo all'asse X, qual è il modulo della proiezione del vettore su questo asse? E che dire del modulo della proiezione dello stesso vettore sull'asse Y?

4. Se il vettore spostamento è parallelo all'asse X, allora il modulo della proiezione del vettore su questo asse è uguale al modulo del vettore stesso e la sua proiezione sull'asse Y è zero.

5. Determina i segni delle proiezioni sull'asse X dei vettori spostamento mostrati nella Figura 22. Come cambiano le coordinate del corpo durante questi spostamenti?

5. In tutti i seguenti casi, la coordinata Y del corpo non cambia e la coordinata X del corpo cambierà come segue:

a) s 1;

la proiezione del vettore s 1 sull'asse X è negativa ed è pari in valore assoluto alla lunghezza del vettore s 1 . Con tale movimento, la coordinata X del corpo diminuirà della lunghezza del vettore s 1.

b) s2;

la proiezione del vettore s 2 sull'asse X è positiva e uguale in grandezza alla lunghezza del vettore s 1 . Con un tale movimento, la coordinata X del corpo aumenterà della lunghezza del vettore s 2.

c) s3;

la proiezione del vettore s 3 sull'asse X è negativa e uguale in grandezza alla lunghezza del vettore s 3 . Con tale movimento, la coordinata X del corpo diminuirà della lunghezza del vettore s 3.

d)s 4;

la proiezione del vettore s 4 sull'asse X è positiva e uguale in grandezza alla lunghezza del vettore s 4 . Con tale movimento, la coordinata X del corpo aumenterà della lunghezza del vettore s 4.

e) s 5;

la proiezione del vettore s 5 sull'asse X è negativa e pari in grandezza alla lunghezza del vettore s 5 . Con tale movimento, la coordinata X del corpo diminuirà della lunghezza del vettore s 5.

6. Se il valore della distanza percorsa è grande, il modulo di spostamento può essere piccolo?

6. Forse. Ciò è dovuto al fatto che lo spostamento (vettore di spostamento) è una quantità vettoriale, cioè è un segmento di linea retta diretto che collega la posizione iniziale del corpo con le sue posizioni successive. E la posizione finale del corpo (indipendentemente dalla distanza percorsa) può essere il più vicino possibile alla posizione iniziale del corpo. Se la posizione finale e quella iniziale del corpo coincidono, il modulo di spostamento sarà pari a zero.

7. Perché nella meccanica il vettore del movimento di un corpo è più importante del percorso che ha percorso?

7. Il compito principale della meccanica è determinare la posizione del corpo in qualsiasi momento. Conoscendo il vettore del movimento del corpo, possiamo determinare le coordinate del corpo, ad es. la posizione del corpo in qualsiasi momento nel tempo, e conoscendo solo la distanza percorsa, non possiamo determinare le coordinate del corpo, perché non abbiamo informazioni sulla direzione del movimento, ma possiamo solo giudicare la lunghezza del percorso percorso in un dato momento.

L'asse è la direzione. Ciò significa che la proiezione su un asse o su una linea diretta è considerata la stessa cosa. La proiezione può essere algebrica o geometrica. In termini geometrici, la proiezione di un vettore su un asse è intesa come un vettore e in termini algebrici come un numero. Cioè, vengono utilizzati i concetti di proiezione di un vettore su un asse e proiezione numerica di un vettore su un asse.

Se abbiamo un asse L e un vettore A B → diverso da zero, allora possiamo costruire un vettore A 1 B 1 ⇀, che denota le proiezioni dei suoi punti A 1 e B 1.

A 1 B → 1 sarà la proiezione del vettore A B → su L.

Definizione 1

Proiezione del vettore sull'asseè un vettore il cui inizio e fine sono proiezioni dell'inizio e della fine di un dato vettore. n p L A B → → è consuetudine denotare la proiezione A B → su L. Per costruire una proiezione su L, le perpendicolari vengono rilasciate su L.

Esempio 1

Un esempio di proiezione vettoriale su un asse.

SU piano delle coordinate Circa x y viene specificato il punto M 1 (x 1 , y 1). È necessario costruire proiezioni su O x e O y per immaginare il raggio vettore del punto M 1. Otteniamo le coordinate dei vettori (x 1, 0) e (0, y 1).

Se parliamo di proiezione di a → su un b diverso da zero → o di proiezione di a → sulla direzione b → , allora intendiamo la proiezione di a → sull'asse con cui coincide la direzione b →. La proiezione di a → sulla retta definita da b → è denominata n p b → a → → . È noto che quando l'angolo compreso tra a → e b → , n p b → a → → e b → possono essere considerati codirezionali. Nel caso in cui l'angolo sia ottuso, n p b → a → → e b → sono in direzioni opposte. In una situazione di perpendicolarità a → e b →, e a → è zero, la proiezione di a → nella direzione b → è il vettore zero.

La caratteristica numerica della proiezione di un vettore su un asse è la proiezione numerica di un vettore su un dato asse.

Definizione 2

Proiezione numerica del vettore sull'asseè un numero uguale al prodotto della lunghezza di un dato vettore e del coseno dell'angolo compreso tra il vettore dato e il vettore che determina la direzione dell'asse.

La proiezione numerica di A B → su L è indicata con n p L A B → , e a → su b → - n p b → a → .

In base alla formula, otteniamo n p b → a → = a → · cos a → , b → ^ , da cui a → è la lunghezza del vettore a → , a ⇀ , b → ^ è l'angolo tra i vettori a → eb → .

Otteniamo la formula per il calcolo della proiezione numerica: n p b → a → = a → · cos a → , b → ^ . È applicabile per lunghezze note a → e b → e per l'angolo tra di loro. La formula è applicabile per le coordinate note a → e b →, ma esiste una forma semplificata.

Esempio 2

Trova la proiezione numerica di a → su una linea retta nella direzione b → con una lunghezza a → pari a 8 e un angolo tra loro di 60 gradi. Per condizione abbiamo a ⇀ = 8, a ⇀, b → ^ = 60 °. Quindi, sostituiamo valori numerici nella formula n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4 .

Risposta: 4.

Noto cos (a → , b → ^) = a ⇀ , b → a → · b → , abbiamo a → , b → come prodotto scalare di a → e b → . Seguendo la formula n p b → a → = a → · cos a ⇀ , b → ^ , possiamo trovare la proiezione numerica a → diretta lungo il vettore b → e ottenere n p b → a → = a → , b → b → . La formula equivale alla definizione data all'inizio del paragrafo.

Definizione 3

La proiezione numerica del vettore a → su un asse coincidente in direzione con b → è il rapporto tra il prodotto scalare dei vettori a → e b → per la lunghezza b → . La formula n p b → a → = a → , b → b → è applicabile per trovare la proiezione numerica di a → su una linea coincidente in direzione con b → , con coordinate a → e b → note.

Esempio 3

Dato b → = (- 3 , 4) . Trovare la proiezione numerica a → = (1, 7) su L.

Soluzione

Sul piano delle coordinate n p b → a → = a → , b → b → ha la forma n p b → a → = a → , b → b → = a x b x + a y b y b x 2 + b y 2 , con a → = (a x , a y ) e b → = b x , b y . Per trovare la proiezione numerica del vettore a → sull'asse L, occorre: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5.

Risposta: 5.

Esempio 4

Trova la proiezione di a → su L, coincidente con la direzione b →, dove sono a → = - 2, 3, 1 eb → = (3, - 2, 6). Lo spazio tridimensionale è specificato.

Soluzione

Dato a → = a x , a y , a z e b → = b x , b y , b z , calcoliamo il prodotto scalare: a ⇀ , b → = a x · b x + a y · b y + a z · b z . La lunghezza b → si trova utilizzando la formula b → = b x 2 + b y 2 + b z 2 . Ne consegue che la formula per determinare la proiezione numerica a → sarà: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .

Sostituisci i valori numerici: n p L a → = n p b → a → = (- 2) 3 + 3 (- 2) + 1 6 3 2 + (- 2) 2 + 6 2 = - 6 49 = - 6 7 .

Risposta: - 6 7.

Consideriamo la connessione tra a → su L e la lunghezza della proiezione a → su L. Disegniamo un asse L, sommando a → e b → da un punto su L, dopodiché tracciamo una linea perpendicolare dall'estremità a → a L e disegniamo una proiezione su L. Esistono 5 varianti dell'immagine:

Primo il caso con a → = n p b → a → → significa a → = n p b → a → → , quindi n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → a → → .

Secondo il caso implica l'uso di n p b → a → ⇀ = a → · cos a → , b → , che significa n p b → a → = a → · cos (a → , b →) ^ = n p b → a → → .

Terzo il caso spiega che quando n p b → a → → = 0 → otteniamo n p b ⇀ a → = a → · cos (a → , b → ^) = a → · cos 90 ° = 0 , allora n p b → a → → = 0 e n p b → un → = 0 = n p b → un → → .

Il quarto il caso mostra n p b → a → → = a → · cos (180 ° - a → , b → ^) = - a → · cos (a → , b → ^) , segue n p b → a → = a → · cos ( a → , b → ^) = - n p b → a → → .

Quinto il caso risulta a → = n p b → a → → , che significa a → = n p b → a → → , quindi abbiamo n p b → a → = a → · cos a → , b → ^ = a → · cos 180° = - a → = - n p b → a → .

Definizione 4

La proiezione numerica del vettore a → sull'asse L, che è orientato allo stesso modo di b →, ha il seguente valore:

• la lunghezza della proiezione del vettore a → su L, a condizione che l'angolo tra a → e b → sia inferiore a 90 gradi o uguale a 0: n p b → a → = n p b → a → → con la condizione 0 ≤ (a → , b →) ^< 90 ° ;
• zero purché a → e b → siano perpendicolari: n p b → a → = 0, quando (a → , b → ^) = 90 °;
• la lunghezza della proiezione a → su L, moltiplicata per -1, quando esiste un angolo ottuso o retto dei vettori a → e b →: n p b → a → = - n p b → a → → con la condizione di 90 °< a → , b → ^ ≤ 180 ° .

Esempio 5

Data la lunghezza della proiezione a → su L, pari a 2. Trovare la proiezione numerica a → purché l'angolo sia 5 π 6 radianti.

Soluzione

Dalla condizione è chiaro che questo angolo è ottuso: π 2< 5 π 6 < π . Тогда можем найти числовую проекцию a → на L: n p L a → = - n p L a → → = - 2 .

Risposta: -2.

Esempio 6

Dato un piano O x y z con un vettore di lunghezza a → pari a 6 3, b → (- 2, 1, 2) con un angolo di 30 gradi. Trovare le coordinate della proiezione a → sull'asse L.

Soluzione

Per prima cosa calcoliamo la proiezione numerica del vettore a →: n p L a → = n p b → a → = a → · cos (a → , b →) ^ = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .

A condizione che l'angolo sia acuto, quindi la proiezione numerica a → = la lunghezza della proiezione del vettore a →: n p L a → = n p L a → → = 9. Questo caso mostra che i vettori n p L a → → e b → sono co-diretti, il che significa che esiste un numero t per il quale l'uguaglianza è vera: n p L a → → = t · b → . Da qui vediamo che n p L a → → = t · b → , il che significa che possiamo trovare il valore del parametro t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 99 = 3 .

Allora n p L a → → = 3 · b → con le coordinate della proiezione del vettore a → sull'asse L pari a b → = (- 2 , 1 , 2) , dove è necessario moltiplicare i valori per 3. Abbiamo n p L a → → = (- 6 , 3 , 6) . Risposta: (- 6, 3, 6).

È necessario ripetere le informazioni precedentemente apprese sulla condizione di collinearità dei vettori.

Se noti un errore nel testo, evidenzialo e premi Ctrl+Invio

Proiezione algebrica di un vettore su qualsiasi asse è uguale al prodotto della lunghezza del vettore e del coseno dell'angolo compreso tra l'asse e il vettore:

Pr a b = |b|cos(a,b) oppure

Dove a b è il prodotto scalare di vettori, |a| - modulo del vettore a.

Istruzioni. Per trovare online la proiezione del vettore Pr a b, è necessario specificare le coordinate dei vettori a e b. In questo caso il vettore può essere specificato nel piano (due coordinate) e nello spazio (tre coordinate). La soluzione risultante viene salvata in un file Word. Se i vettori vengono specificati tramite le coordinate dei punti, è necessario utilizzare questa calcolatrice.

Classificazione delle proiezioni vettoriali

Tipi di proiezioni per definizione proiezione vettoriale

1. La proiezione geometrica del vettore AB sull'asse (vettore) è chiamata vettore A"B", il cui inizio A' è la proiezione dell'inizio A sull'asse (vettore) e la fine B' è la proiezione dell'estremità B sullo stesso asse.
2. La proiezione algebrica del vettore AB sull'asse (vettore) è detta lunghezza del vettore A"B", presa con segno + o -, a seconda che il vettore A"B" abbia la stessa direzione dell'asse ( vettore).

Tipi di proiezioni secondo il sistema di coordinate

Proprietà della proiezione vettoriale

1. La proiezione geometrica di un vettore è un vettore (ha una direzione).
2. La proiezione algebrica di un vettore è un numero.

Teoremi della proiezione vettoriale

Teorema 1. La proiezione della somma dei vettori su un asse qualsiasi è uguale alla proiezione degli addendi dei vettori sullo stesso asse.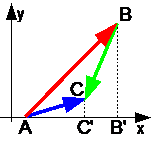

AC" =AB" +B"C"

Teorema 2. La proiezione algebrica di un vettore su qualsiasi asse è uguale al prodotto della lunghezza del vettore e del coseno dell'angolo formato dall'asse e dal vettore:

Pr a b = |b|·cos(a,b)

Tipi di proiezioni vettoriali

1. proiezione sull'asse OX.
2. proiezione sull'asse OY.
3. proiezione su un vettore.

Proiezione sull'asse OX	Proiezione sull'asse OY	Proiezione su vettore
Se la direzione del vettore A’B’ coincide con la direzione dell’asse OX, allora la proiezione del vettore A’B’ ha segno positivo.	Se la direzione del vettore A’B’ coincide con la direzione dell’asse OY, allora la proiezione del vettore A’B’ ha segno positivo.	Se la direzione del vettore A’B’ coincide con la direzione del vettore NM, allora la proiezione del vettore A’B’ ha segno positivo.
Se la direzione del vettore è opposta alla direzione dell’asse OX, allora la proiezione del vettore A’B’ ha segno negativo.	Se la direzione del vettore A’B’ è opposta alla direzione dell’asse OY, allora la proiezione del vettore A’B’ ha segno negativo.	Se la direzione del vettore A’B’ è opposta alla direzione del vettore NM, allora la proiezione del vettore A’B’ ha segno negativo.
Se il vettore AB è parallelo all’asse OX, allora la proiezione del vettore A’B’ è uguale al valore assoluto del vettore AB.	Se il vettore AB è parallelo all'asse OY, la proiezione del vettore A'B' è uguale al valore assoluto del vettore AB.	Se il vettore AB è parallelo al vettore NM, allora la proiezione del vettore A’B’ è uguale al valore assoluto del vettore AB.
Se il vettore AB è perpendicolare all’asse OX, allora la proiezione A’B’ è uguale a zero (vettore nullo).	Se il vettore AB è perpendicolare all’asse OY, allora la proiezione A’B’ è uguale a zero (vettore nullo).	Se il vettore AB è perpendicolare al vettore NM, allora la proiezione A’B’ è uguale a zero (vettore nullo).

1. Domanda: La proiezione di un vettore può avere segno negativo? Risposta: Sì, il vettore di proiezione può avere un valore negativo. In questo caso il vettore ha verso opposto (vedi come sono diretti l'asse OX e il vettore AB)
2. Domanda: La proiezione di un vettore può coincidere con il valore assoluto del vettore? Risposta: sì, può. In questo caso i vettori sono paralleli (o giacciono sulla stessa retta).
3. Domanda: La proiezione di un vettore può essere uguale a zero (vettore nullo). Risposta: sì, può. In questo caso il vettore è perpendicolare all'asse corrispondente (vettore).

Esempio 1. Il vettore (Fig. 1) forma un angolo di 60° con l'asse OX (è specificato dal vettore a). Se OE è un'unità di scala, allora |b|=4, quindi .

Infatti, la lunghezza del vettore ( proiezione geometrica b) è uguale a 2, e la direzione coincide con la direzione dell'asse OX.

Esempio 2. Il vettore (Fig. 2) forma un angolo (a,b) = 120 o con l'asse OX (con il vettore a). Lunghezza |b| il vettore b è uguale a 4, quindi pr a b=4·cos120 o = -2.

Infatti la lunghezza del vettore è 2 e la direzione è opposta alla direzione dell'asse.

Proiezione vettore su un asse è un vettore che si ottiene moltiplicando la proiezione scalare di un vettore su questo asse e il vettore unitario di questo asse. Ad esempio, se x – proiezione scalare vettore UN all'asse X, quindi una x io- la sua proiezione vettoriale su questo asse.

Denotiamo proiezione vettoriale uguale al vettore stesso, ma con l'indice dell'asse su cui è proiettato il vettore. Quindi, la proiezione vettoriale del vettore UN sull'asse X indichiamo UN X ( grasso una lettera che denota un vettore e un pedice del nome dell'asse) o (una lettera non in grassetto che denota un vettore, ma con una freccia in alto (!) e un pedice del nome dell'asse).

Proiezione scalare viene chiamato il vettore per asse numero, il cui valore assoluto è pari alla lunghezza del segmento dell'asse (sulla scala selezionata) racchiuso tra le proiezioni del punto iniziale e del punto finale del vettore. Di solito invece dell'espressione proiezione scalare dicono semplicemente - proiezione. La proiezione è indicata con la stessa lettera del vettore proiettato (nella scrittura normale, non in grassetto), con un indice inferiore (di regola) del nome dell'asse su cui questo vettore è proiettato. Ad esempio, se un vettore viene proiettato sull'asse X UN, quindi la sua proiezione è indicata con una x. Quando si proietta lo stesso vettore su un altro asse, se l'asse è Y, la sua proiezione sarà indicata con y.

Per calcolare la proiezione vettore su un asse (ad esempio l'asse X), è necessario sottrarre la coordinata del punto iniziale dalla coordinata del suo punto finale, ovvero
un x = x k − x n.
La proiezione di un vettore su un asse è un numero. Inoltre, la proiezione può essere positiva se il valore x k è maggiore del valore x n,

negativo se il valore x k è inferiore al valore x n

e uguale a zero se x k è uguale a x n.

La proiezione di un vettore su un asse può essere trovata anche conoscendo il modulo del vettore e l'angolo che forma con tale asse.

Dalla figura è chiaro che a x = a Cos α

cioè, la proiezione del vettore sull'asse è uguale al prodotto del modulo del vettore e del coseno dell'angolo compreso tra la direzione dell'asse e direzione del vettore. Se l'angolo è acuto, allora
Cos α > 0 e a x > 0 e, se ottuso, il coseno dell'angolo ottuso è negativo e anche la proiezione del vettore sull'asse sarà negativa.

Gli angoli misurati dall'asse in senso antiorario sono considerati positivi mentre gli angoli misurati lungo l'asse sono negativi. Tuttavia, poiché il coseno è una funzione pari, cioè Cos α = Cos (− α), quando si calcolano le proiezioni, gli angoli possono essere contati sia in senso orario che antiorario.

Per trovare la proiezione di un vettore su un asse, il modulo di questo vettore deve essere moltiplicato per il coseno dell'angolo formato dalla direzione dell'asse alla direzione del vettore.

Coordinate vettoriali— coefficienti dell'unica combinazione lineare possibile di vettori di base nel sistema di coordinate selezionato, uguali al vettore dato.

dove sono le coordinate del vettore.

Prodotto scalare vettori

Prodotto scalare di vettori[- in dimensione finita spazio vettorialeè definito come la somma dei prodotti di componenti identici moltiplicati vettori.

Ad esempio la S.p.v. UN = (UN 1 , ..., UN) E B = (B 1 , ..., b n):

(UN , B ) = UN 1 B 1 + UN 2 B 2 + ... + a n b n