Lezione pratica "calcolo delle derivate". Lezione pratica "calcolo delle derivate" Trova la derivata della funzione y
Obiettivi della lezione:
Educativo- conoscere le formule di differenziazione; regole di differenziazione;
differenziazione di una funzione complessa; significato fisico e geometrico della derivata;
Equazione della tangente al grafico di una funzione.
Sviluppo - essere in grado di trovare le derivate di funzioni; risolvere problemi utilizzando significato fisico, significato geometrico; trovare il valore della derivata di una funzione in un punto; spiegare e giustificare matematicamente correttamente le azioni eseguite.
Educativo – coltivare l’indipendenza, la responsabilità, la riflessione.
Durante le lezioni
I. Momento organizzativo.
II. Controllo dei compiti
(durante le pause, i consulenti controllano (gli studenti) e assegnano i voti).
III. Definizione degli obiettivi e motivazione
L'insegnante informa gli studenti che questa lezione è l'ultima lezione sull'argomento “Calcolo delle derivate” e li invita a formulare i propri obiettivi.
Insegnante: "Il grande filosofo Confucio una volta disse: "Tre percorsi conducono alla conoscenza: il percorso della riflessione è il percorso più nobile, il percorso dell'imitazione è il percorso più semplice e il percorso dell'esperienza è il percorso più amaro". Quindi oggi in classe, ciascuno di voi determinerà quale percorso verso la conoscenza di questo argomento si trova”.
Agli studenti viene affidato il compito di dimostrare le proprie conoscenze e abilità nel calcolo delle derivate e viene loro fornito un programma di lezione.
Fase I: Completare l'attività utilizzando la carta "Ricorda".
(verifica della conoscenza di formule e regole di differenziazione).
Fase II: Lavoro frontale orale sulla ripetizione e generalizzazione delle conoscenze.
Fase III:"Previsione del test" (quando si esegue questa attività, l'aiuto di consulenti è accettabile).
IOFase V: Soluzione di un problema pratico.
Fase V: Lavoro indipendente
Vengono valutate le fasi I, III, V del lavoro e dei compiti a casa. I consulenti controllano e inseriscono i risultati nella tabella di valutazione.
Criteri di valutazione: "5"- 19-20 punti;
"4"- 15-18 punti;
"3"- 10-14 punti.
Percorsi di conoscenza
- Riproduzione e correzione delle conoscenze di riferimento
Fase I.
Bersaglio: controllo, autocontrollo della conoscenza delle formule e delle regole di differenziazione
Ricordare! FI ___________________________________________________ |
|
Derivato |
|
c,c - contro T |
|
|
|
|
|
F"(x)+ G"(X) |
|
F(X)* G(X) |
|
|
|
Al termine di questa attività, viene eseguito un autotest utilizzando la “Tabella dei derivati”. Le carte vengono consegnate ai consulenti per la verifica (non sono consentite correzioni sulle carte).
V. Generalizzazione e sistematizzazione della conoscenza
Fase II.
1. Lavoro frontale orale.
UN. Genera un'attività per questa condizione e risolvila.
![]()
1. Trova il valore della derivata della funzione nel punto t = 3. (Risposta: 21.)
2. Crea un'equazione per la tangente al grafico della funzione nel punto t = 3. (Risposta: y = 21x-45.).
3. Trova la velocità del corpo e l'accelerazione nel momento t=3c, se la legge del movimento è data dalla formula. (Risposta: 21 m/s, 16 m/s²).
4. Trova il coefficiente angolare della tangente tracciata al grafico della funzione nel punto t = 3. (Risposta: 21.).
5. Trova la tangente dell'angolo di inclinazione della tangente al grafico della funzione nel punto t = 3 e determina il tipo di angolo tra la tangente e la direzione positiva dell'asse Ox. (Risposta: tgα, l'angolo α è acuto)
B. Trova le derivate di funzioni

2. Fase III“Previsione di prova”


Al termine di questa attività, viene eseguito un autotest basato sulle risposte finali e i test vengono consegnati ai consulenti. (non sono ammesse correzioni sulle carte).
Risposte:
1 opzione |
||||
opzione 2 |
- La soluzione del problema
IOFase V
Soluzione frontale ad un problema di livello avanzato (la soluzione viene effettuata dai consulenti insieme alla classe).
Compito
A quali valori dei parametri UN tangenti al grafico di una funzione ![]()
tracciati nei punti della sua intersezione con l'asse X, formano tra loro un angolo di 60°?

Il grafico è una parabola con rami ascendenti che intersecano l'asse X in due punti (caso UN=0 non soddisfa il significato del problema):
IX. Riassumendo e valutando
1. Domande: a) Lo scopo della lezione è stato raggiunto?
b) Quale fase ti è sembrata la più difficile?
c) Qual è stata la cosa più interessante?
2. I consulenti annunciano i risultati (numero e nomi degli studenti in arrivo
imitazione, modi di riflessione e modi di esperienza).
Lavoro pratico
matematica
1. Trovare il limite di una funzione. Il primo e il secondo sono limiti meravigliosi.
2. Derivato di una funzione complessa. Studio di una funzione di una variabile e tracciamento di grafici.
3. Prova “Applicazione del calcolo differenziale allo studio delle funzioni”.
4. Trovare integrali indefiniti. Calcolo di integrali definiti.
5. Calcolo dei determinanti.
6. Risoluzione di sistemi di equazioni lineari utilizzando il metodo Cramer. Test.
7. Risoluzione dei problemi sull'argomento "Set". Formule dell'algebra logica.
8. Calcolo delle probabilità di eventi casuali. Formula della probabilità totale.
9. Calcolo delle caratteristiche numeriche.
10. Test “Fondamenti di teoria della probabilità e statistica matematica”
11. Forma trigonometrica di un numero complesso.
12. Azioni con numeri complessi in varie forme.
ISTRUZIONI METODOLOGICHE PER IL LAVORO PRATICO IN MATEMATICA
CORSO 2
Una lezione pratica è una forma di organizzazione del processo educativo, che coinvolge gli studenti che eseguono uno o più lavori pratici su incarico e sotto la guida di un insegnante.
Pertanto, nelle lezioni pratiche di matematica, gli studenti sviluppano la capacità di risolvere problemi, che in futuro dovrebbero essere utilizzati per risolvere problemi professionali in discipline speciali.
Nel corso del lavoro pratico, gli studenti acquisiscono la capacità di utilizzare fonti di informazione, lavorare con documenti normativi e materiale didattico, libri di consultazione, realizzare disegni, diagrammi, tabelle, risolvere vari tipi di problemi ed effettuare calcoli.
Problemi che vengono risolti durante le lezioni pratiche di matematica:
1) ampliamento e consolidamento delle conoscenze teoriche in matematica acquisite durante le lezioni frontali;
2) sviluppare negli studenti le abilità pratiche e le abilità necessarie per risolvere con successo problemi di matematica;
3) sviluppo del bisogno di autoeducazione degli studenti e miglioramento delle conoscenze e delle competenze nel processo di studio della matematica;
4) formazione di un atteggiamento creativo e un approccio di ricerca nel processo di studio della matematica;
5) formazione di qualità professionalmente significative di un futuro specialista e capacità nell'applicazione delle conoscenze acquisite nel campo professionale.
Lezione pratica n. 1. Calcolo dei limiti di funzione. Il primo e il secondo sono limiti meravigliosi.
Soggetto : Calcolo dei limiti di funzione.
Bersaglio: acquisizione delle conoscenze di base nel campo dei rami fondamentali della matematica . Testare l'assimilazione delle conoscenze sul calcolo dei limiti delle funzioni. Ripetere e sistematizzare la conoscenza su questo argomento.
Compiti:
Sviluppo del pensiero professionale creativo;
Padronanza del linguaggio scientifico, capacità di operare concetti;
Padroneggiare le capacità di impostazione e risoluzione dei problemi;
Approfondimento della formazione teorica e pratica;
Sviluppo dell'iniziativa e dell'indipendenza degli studenti.
Rafforzare le competenze informatiche;
Continua a lavorare sul discorso matematico.
Formazione di competenze per il lavoro indipendente, lavoro con un libro di testo, competenze per acquisire conoscenze in modo indipendente;
Sviluppo della capacità di evidenziare la cosa principale quando si lavora con il testo;
Formazione del pensiero indipendente, operazioni mentali: confronto, analisi, sintesi, generalizzazione, analogia;
Mostrare agli studenti il ruolo del lavoro sistematico per approfondire e aumentare la forza della conoscenza, sulla cultura del completamento dei compiti;
Sviluppo delle capacità creative degli studenti.
Fornire lavoro pratico:
Materiale teorico di raccomandazioni metodologiche per il lavoro pratico.
Matematica, – Serie: Istruzione professionale secondaria. - “La Fenice” di Rostov sul Don, p.
Avanzamento della lezione pratica.
1.Formulazione dell'argomento della lezione, spiegazione della connessione dell'argomento con altri argomenti della disciplina accademica;
2.Verificare la preparazione degli studenti per la lezione;
3. Condurre la lezione vera e propria in base all'argomento e in conformità con il programma di lavoro della disciplina:
Studia materiale teorico sull'argomento "Calcolo dei limiti delle funzioni".
Considera esempi di risoluzione di compiti tipici.
Svolgi un lavoro indipendente sul calcolo dei limiti delle funzioni utilizzando il primo e il secondo limite notevole.
Rispondere alle domande di sicurezza.
Informazioni teoriche e raccomandazioni metodologiche
sulla risoluzione dei problemi.
1. Presentazione del materiale teorico.
Per calcolare il limite di una funzione in un punto, è necessario:
1) Sostituisci al posto della variabile x ciò a cui tende x.
2) Se dopo aver completato il passaggio 1) otteniamo un'incertezza del modulo https://pandia.ru/text/78/405/images/image003_6.png" width="19" Height="22 src=">e sostituiamo la freccia con il segno meno: (x-a).
3) Se, dopo aver completato il passaggio 1), riceviamo un'incertezza del modulo https://pandia.ru/text/78/405/images/image002_13.png" width="18" Height="31 src="> associati ai valori delle funzioni trigonometriche, dobbiamo utilizzare il primo limite notevole.
Definizione. Il primo limite notevole è chiamato limite
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Definizione:Il secondo limite notevole chiamato limite

Il numero dato da questo limite gioca un ruolo molto importante sia nell'analisi matematica che in altri rami della matematica. Il numero viene chiamato base dei logaritmi naturali ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Consolidamento del materiale studiato.
Esempio 1
https://pandia.ru/text/78/405/images/image015_1.png" larghezza="28" altezza="30 src=">= -4
Abbiamo usato la regola 1) e abbiamo sostituito al posto di x ciò a cui x dovrebbe tendere, cioè x=2.
Esempio 2
https://pandia.ru/text/78/405/images/image017_1.png" larghezza="154" altezza="32 src=">.png" larghezza="21" altezza="30 src=">= 5
Esempio 3
https://pandia.ru/text/78/405/images/image021_1.png" larghezza="199" altezza="37 src=">.png" larghezza="137" altezza="35 src=">. png" larghezza="138" altezza="24 src=">=3+3=6
Esempio 4
https://pandia.ru/text/78/405/images/image004_7.png" larghezza="22" altezza="31 src=">.png" larghezza="104" altezza="46 src=">. png" altezza="30 src=">
Esempio 5
https://pandia.ru/text/78/405/images/image032_0.png" larghezza="61" altezza="46 src=">.png" altezza="30 src=">=2
Esempio 6
https://pandia.ru/text/78/405/images/image036_0.png" larghezza="18" altezza="28 src=">
B) 
V) 
3. Consolidamento di conoscenze, competenze e abilità.
Svolgere un lavoro indipendente sul calcolo dei limiti delle funzioni.
Lavoro pratico n. 1. opzione 1 Calcola il limite della funzione: 1. 2. 3. 10. | Lavoro pratico n. 1. opzione 2 Calcola il limite della funzione: 1. 2. 3. 10. |
Lavoro pratico n. 2.
Soggetto : Trovare la derivata di una funzione. Studio di una funzione di una variabile e tracciatura di un grafico.
Bersaglio : Testare nella pratica la conoscenza del concetto di derivata di una funzione, la capacità di trovare le derivate di funzioni elementari, funzioni complesse, funzioni inverse, utilizzando la tabella delle derivate e le regole di differenziazione, il concetto di funzione complessa e inversa, la capacità utilizzare una derivata per studiare le funzioni.
Fornire lavoro pratico:
Manuale. "Matematica". – M.: Otarda, 2010.
Matematica. M: Forum-Infa 2008.
Carte individuali con una pratica opzione di lavoro.
1. Materiale teorico ed esempi per trovare la derivata di una funzione.
Definizione: La derivata della funzione f(x) (f"(x)) nel punto x è il limite del rapporto tra l'incremento della funzione e l'incremento dell'argomento quando l'incremento dell'argomento tende a zero:
https://pandia.ru/text/78/405/images/image061_0.png" larghezza="209 altezza=235" altezza="235">
Regole di differenziazione.
Se le funzioni f(x) e g(x) hanno derivate, allora
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, dove C=cost
5..png" larghezza="49" altezza="54 src=">
6. Derivato di una funzione complessa:
f′(g(x))=f′(g) g′(x)
2. Esempi.
1..png" larghezza="61" altezza="41 src=">.png" larghezza="20" altezza="41 src=">.png" larghezza="20" altezza="41 src="> .png" larghezza="69" altezza="41 src=">+4).
La funzione è il prodotto di due fattori: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" Height="41 src=">.png" width=" 64" altezza="41 src=">.png" larghezza="19" altezza="41 src=">.png" larghezza="45" altezza="51 src=">.
La funzione è il quoziente di due espressioni: u=https://pandia.ru/text/78/405/images/image079.png" width="52" Height="41 src=">..png" width= "215" " altezza="57 src=">.png" larghezza="197 altezza=36" altezza="36">
Soluzione. Troviamo la derivata di questa funzione utilizzando la regola di differenziazione delle funzioni complesse (formula 6):

5. Se , allora 
6. sì = X 3 – 3X 2 + 5X+ 2. Troviamo sì "(–1).
sì " = 3X 2 – 6X+ 5. Pertanto, sì "(–1) = 14.
7. Se sì= registro X cos X, Quello sì" = (ln X)"cos X+ln X(cos X) " =1/X∙cos X–ln X peccato X.
Sia data una funzione. Per studiarlo è necessario:
1) Trova il suo dominio di definizione. Se non è troppo difficile, è utile anche trovare la portata. (Tuttavia, in molti casi, la questione della ricerca viene posticipata fino a quando non vengono trovati gli estremi della funzione.)
2) Scopri le proprietà generali della funzione che aiuteranno a determinarne il comportamento: se la funzione è pari o dispari, se è periodica.
3) Scopri come si comporta la funzione quando l'argomento si avvicina ai punti di confine del dominio di definizione, se esistono tali punti di confine. Se una funzione ha punti di discontinuità, allora questi punti dovrebbero essere controllati anche per la presenza di asintoti verticali della funzione. Trova gli asintoti obliqui.
4) Trovare i punti di intersezione del grafico con gli assi delle coordinate, che consiste semplicemente nel calcolare il valore della funzione sotto la condizione:
Con asse OX: y=0;
Con asse OY: x=0.
Trovare i punti di intersezione con l'asse può portare alla necessità di risolvere un'equazione algebrica complessa, cosa che, forse, può essere fatta solo approssimativamente. Trovate le radici della funzione e i punti di discontinuità, possiamo determinare il segno della funzione in ciascuno degli intervalli tra questi punti. Questo può essere fatto calcolando il valore della funzione in qualsiasi punto dell'intervallo o utilizzando il metodo dell'intervallo.
5) Trova intervalli di monotonicità. Per fare ciò, trova la derivata e risolvi la disuguaglianza:
https://pandia.ru/text/78/405/images/image089.png" width="49" Height="19 src=">, la funzione sta diminuendo.
Trovati gli intervalli di monotonicità, possiamo immediatamente determinare i punti di estremo locale: dove un aumento è sostituito da una diminuzione, si trovano dei massimi locali, e dove una diminuzione è sostituita da un aumento, si trovano dei minimi locali.
6) La ricerca degli intervalli di convessità e concavità viene effettuata utilizzando la derivata seconda..png" width="39" Height="19 src="> sugli intervalli:
se https://pandia.ru/text/78/405/images/image090.png" width="39" Height="19 src=">‹0, la curva del grafico della funzione è convessa.
Allo stesso tempo, definiamo punti di flesso come quei punti in cui la funzione cambia la direzione della convessità (ed è continua).
7) Trovare i punti di intersezione del grafico con l'asintoto e i punti aggiuntivi. Questo punto non è obbligatorio, ma il ritrovamento di tali punti rende completo e completo lo studio della funzione e del suo grafico.
Si noti che è utile tracciare immediatamente sul disegno i punti sugli assi coordinati e sul grafico che si ottengono durante lo studio delle funzioni. Questo aiuta a comprendere l'aspetto del grafico lungo il percorso.
3. Fai da te:
|
opzione | Trova la derivata della funzione y: |
opzione | Trova la derivata della funzione y: |
1.y=6- | 1.y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Lezione pratica
Soggetto: Trovare le derivate. Applicazione della derivata allo studio di funzioni e al disegno di grafici.
Bersaglio: Padroneggia il calcolo delle derivate, impara a esplorare una funzione utilizzando la derivata
Mezzi di istruzione: quaderni per esercitazioni pratiche, presentazioni sull'argomento, risorse Internet.
1. Considerare il materiale teorico sugli argomenti: "Regole per il calcolo delle derivate", "Estremo di una funzione", "Convessità, concavità. Punto di flesso."
2. Esamina esempi di compiti.
3. Completa l'attività di prova n. 1.
Domande di controllo:
1. Definire il massimo (minimo) di una funzione in un punto. Cosa si può dire del segno dell'incremento della funzione in un intorno abbastanza piccolo del punto massimo (minimo)?
2. Quali sono le condizioni necessarie per l'esistenza di un estremo di una funzione? Qual è il loro significato geometrico?
3. Qual è la regola per trovare i valori più grandi e più piccoli di una funzione su un segmento?
4. Definire la convessità (concavità) di una curva su un intervallo.
5. Qual è la regola per trovare gli intervalli di convessità e concavità di una curva?
6. Punto di flesso della curva. Come trovarla?
7. Qual è l'algoritmo per costruire un grafico di una funzione?
Regole per il calcolo dei derivati
Derivata di una funzione complessa.
Se A=ƒ( E), u=φ(x), quindi A¢ ( X)=ƒ¢ (i)·φ¢ (X).
Derivato di una somma.
Se A(X)=E(X)+v (X), Quello A¢ (X)=E¢ (X)+v ¢ (X)
Derivato del prodotto.
Se y(x)=u(X)· v (X), Quello A¢ = E¢ · v + tu · v ¢ .
In particolare, ( Con· E)¢ = c· E¢, cioè il fattore costante viene tolto da sotto il segno della derivata. È facile verificarlo
(tu 2 ) ¢ = 2 u·u ¢ , (u 3 ) ¢ =3u 2 tu ¢ , … , (u N ) ¢ =n·u n–1 tu ¢ .
Derivata del quoziente.
Se poi  .
.
Tabella dei derivati
1. (Con)¢ =0
Per una funzione complessa: se u=u(x), Quello:
2. (X)¢ =1
3. (X α )¢ = α · Xα–1, UN– qualsiasi numero reale.
 .
.
3. 
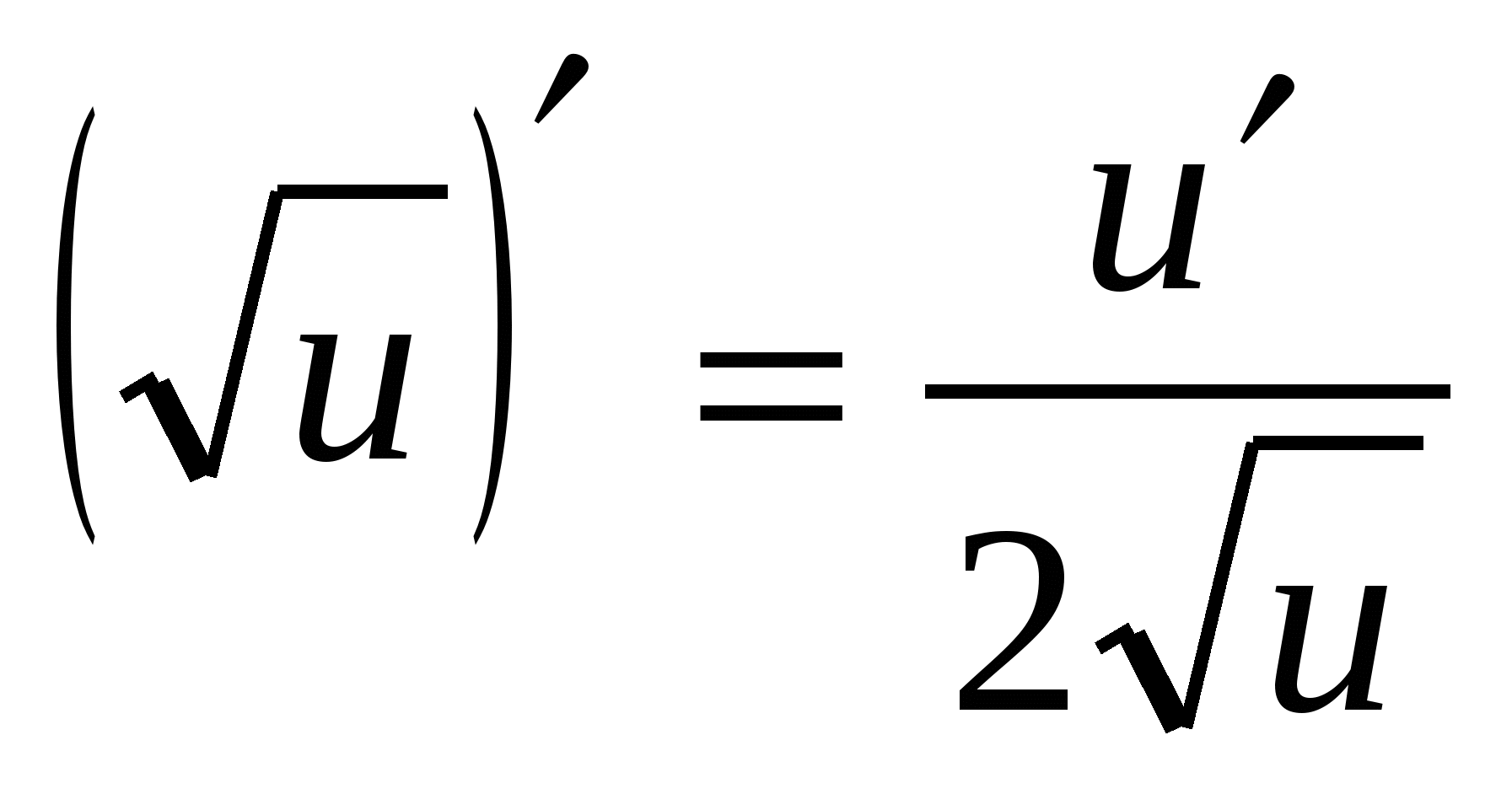
4. (UN X ) ¢ =a X · ln UN
4. 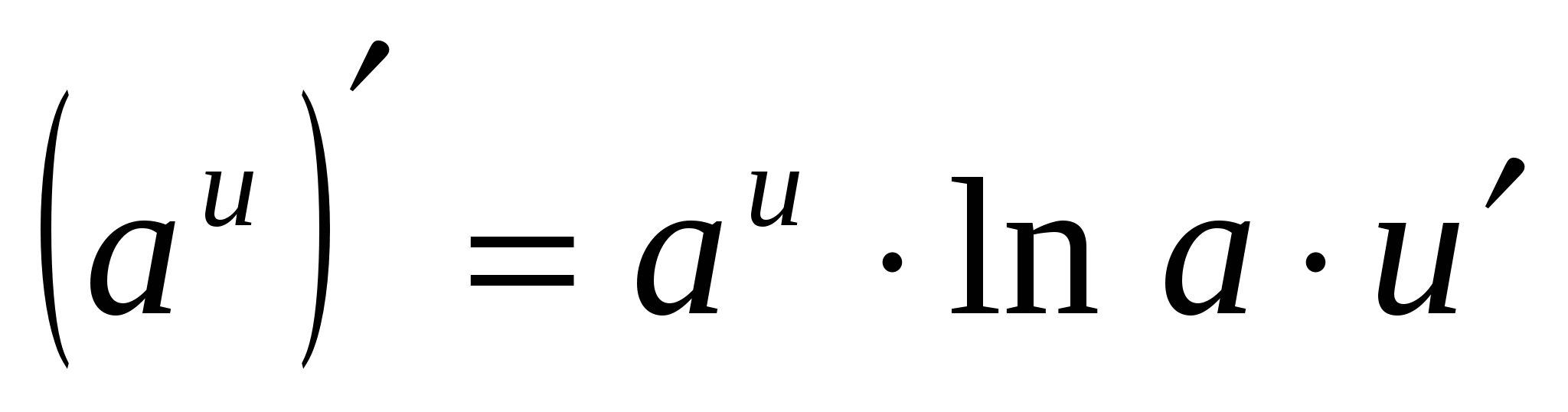
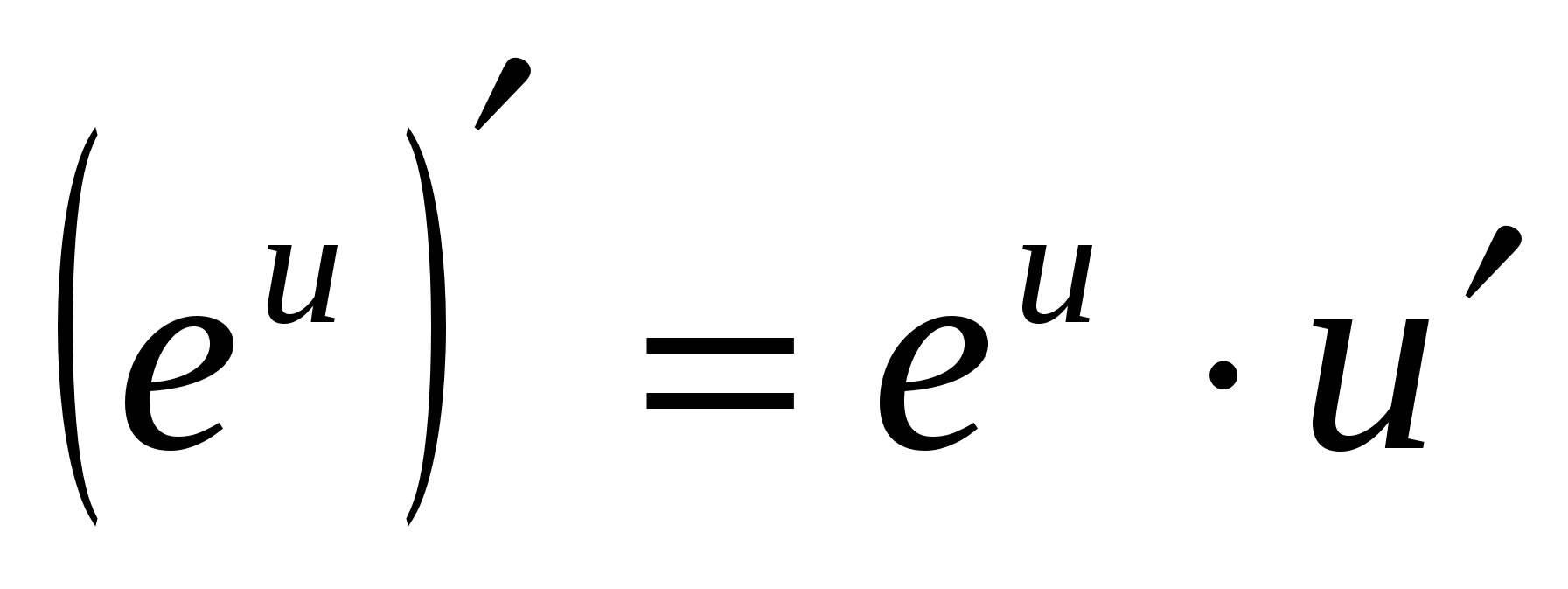
5. (tronco d'albero
UN
X)
¢
=
 .
.
5. 

6. (peccato x)¢ =cosx
6. 
7. (cos x)¢ = –peccato x
7. 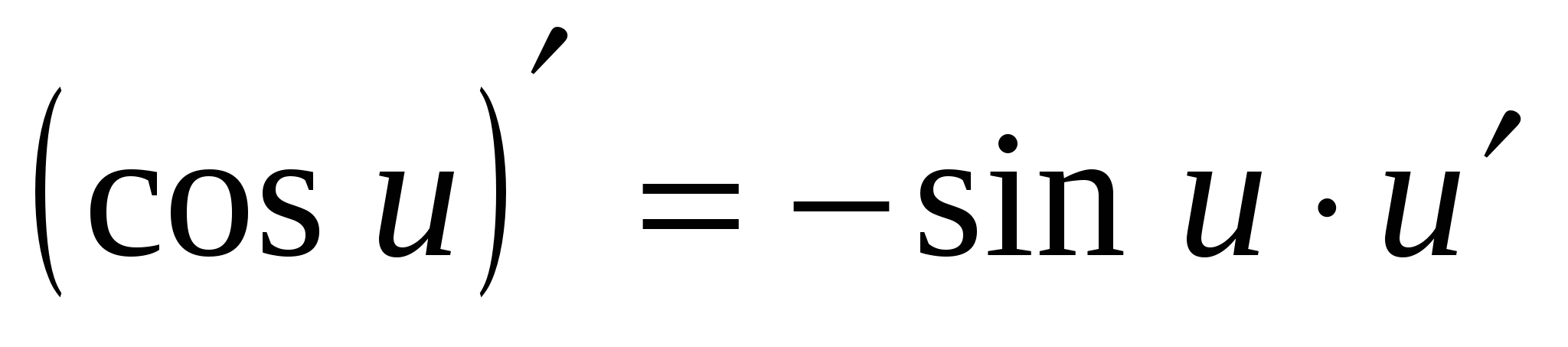
8. (tgx)¢
=
8. 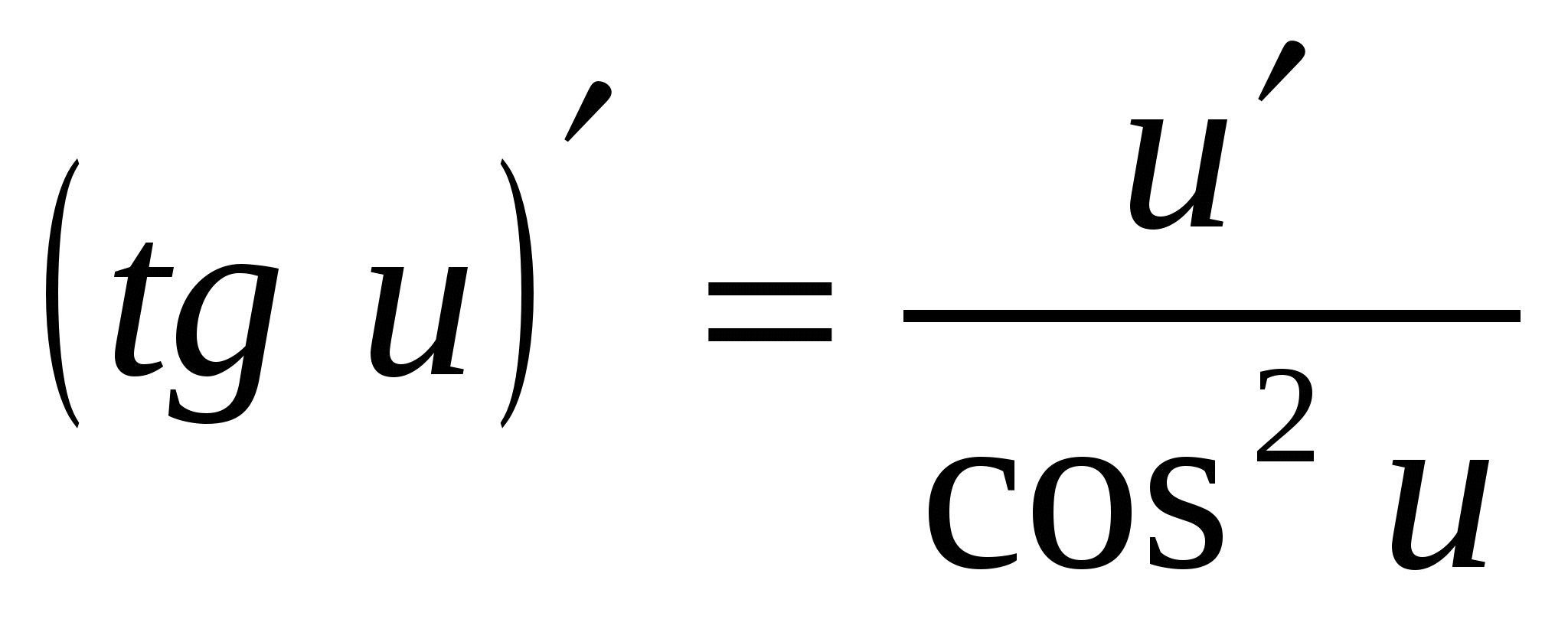
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 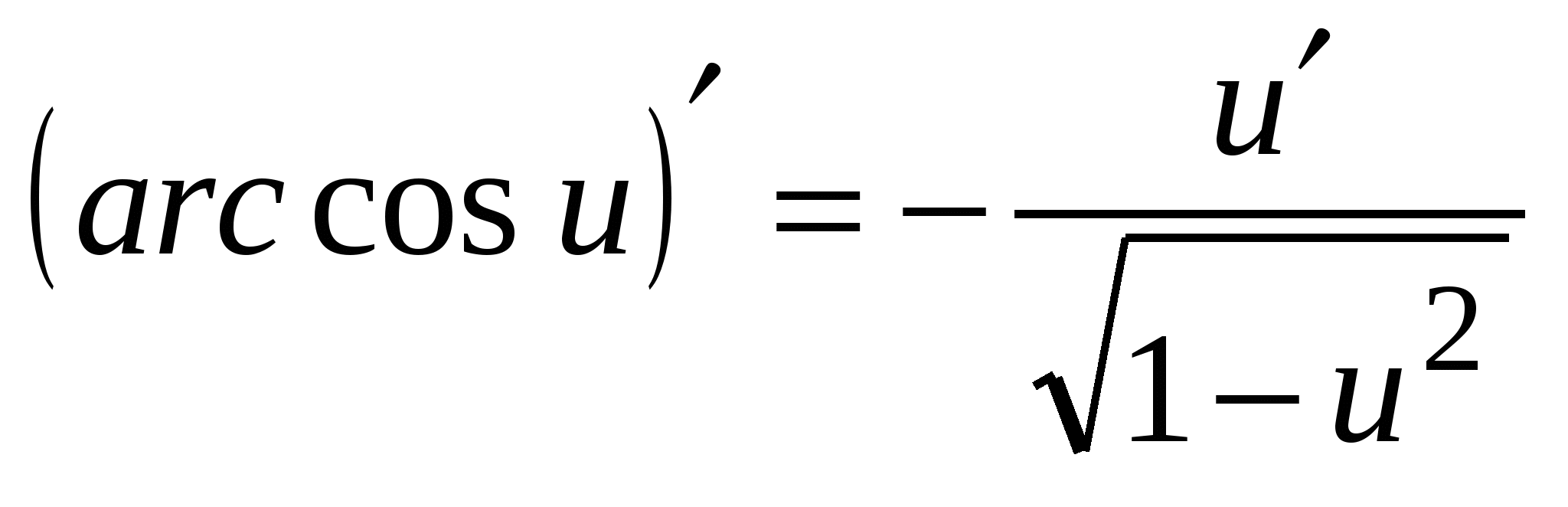
12. 
12. 
13. 
13. 
Esempi di revisione
Esempio 1.
y=(3–2 peccato 5x ) 4 | Applichiamo formule derivate per E α ,peccato tu |
sì ¢ =4·(3–2·sin5x) 3·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
Esempio 2.
. 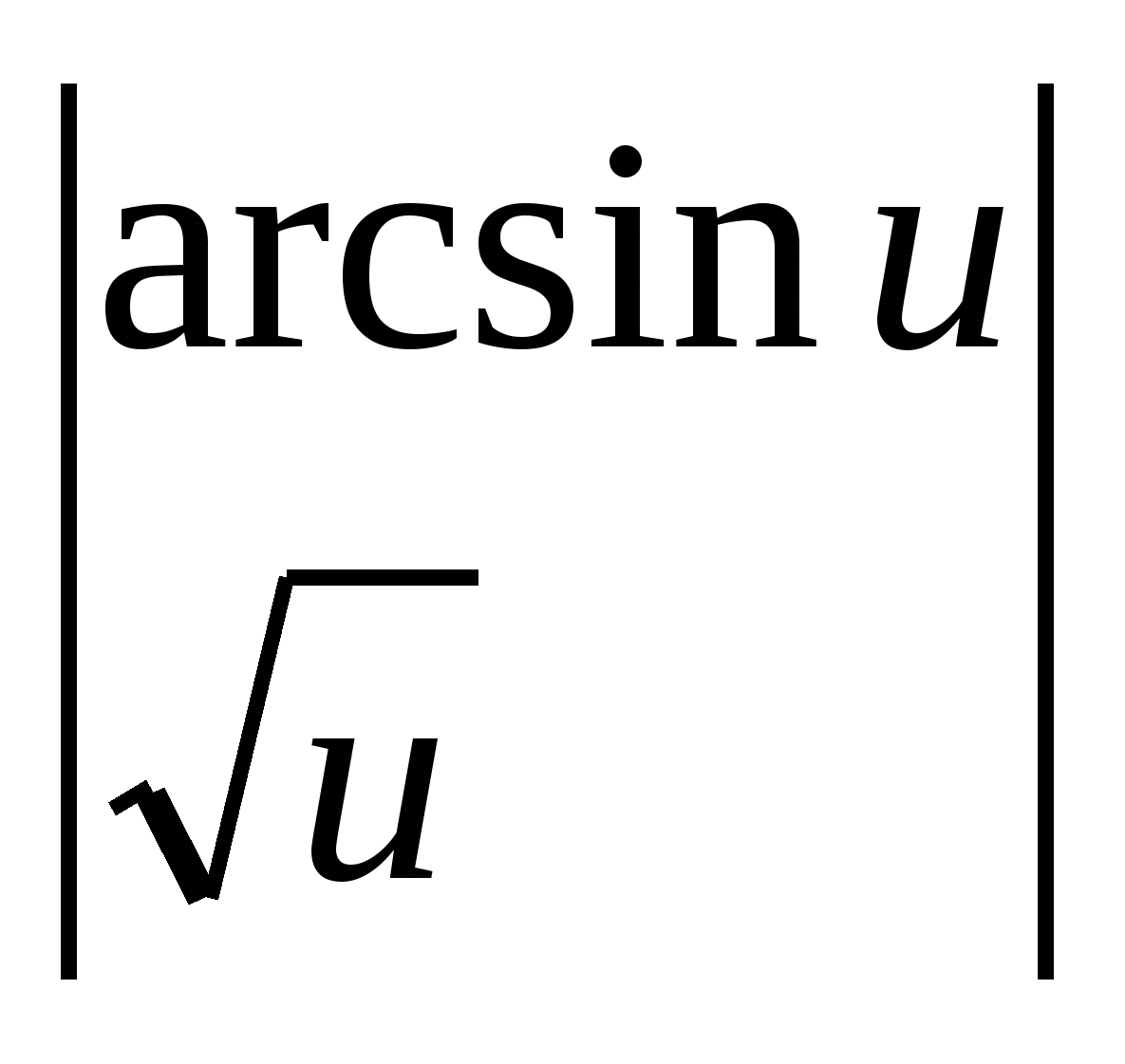

Esempio 3.
 .
. 

Esempio 4.



Esempio 5.
 .
. 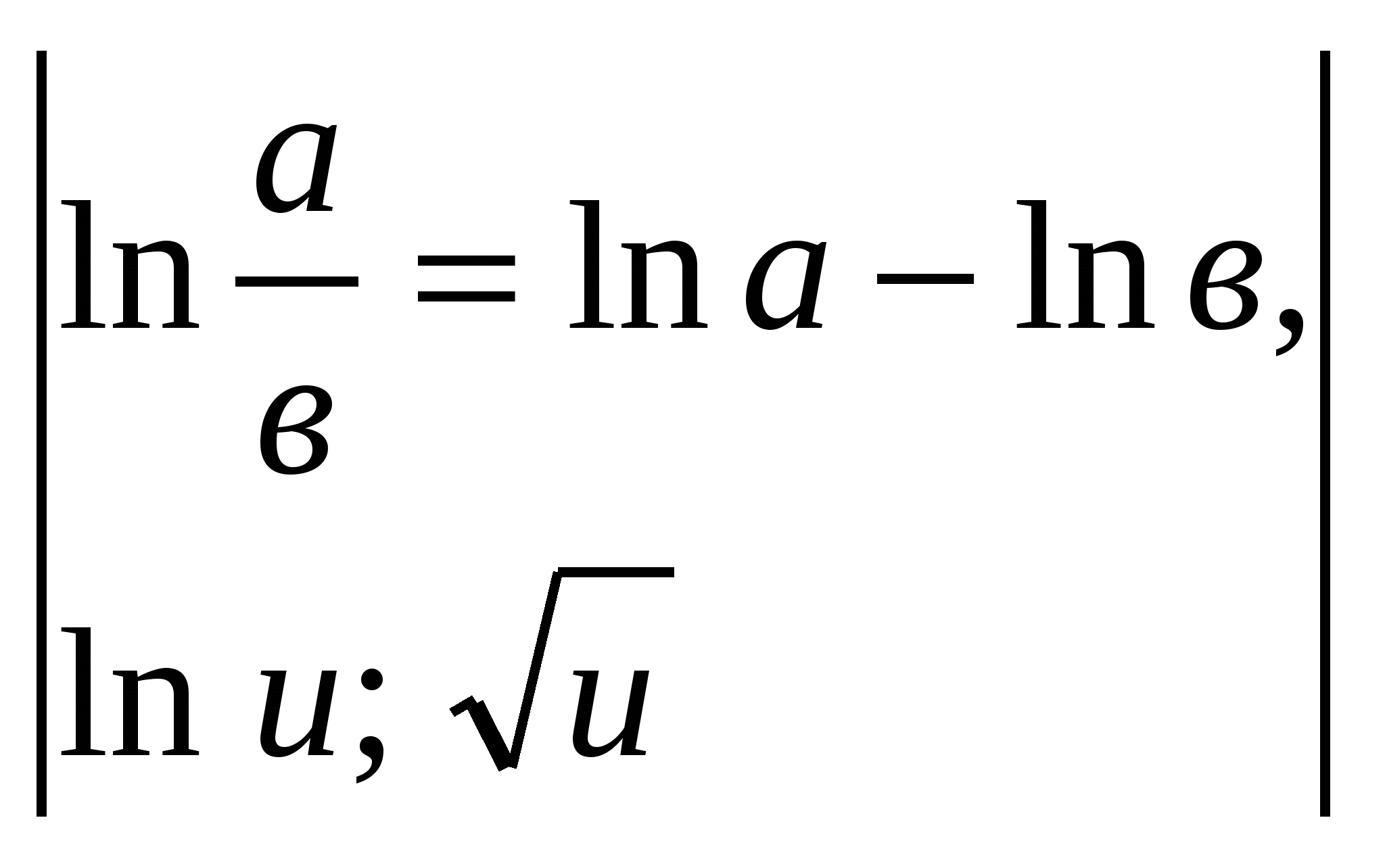

Estremo della funzione
Lo studio di una funzione estrema è una delle applicazioni più importanti delle derivate. Diamo un'occhiata alla definizione di minimi e massimi e come trovarli.
Sia la funzione ƒ( X) è definito e differenziabile su un certo insieme e un punto X 0 è un punto al suo interno.
Definizione. Funzione ƒ (X) al punto X 0 ha massimo(minimo), se esiste un tale intorno del punto X 0, che è per tutti X da questa zona ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Punto X 0 viene quindi chiamato punto massimo(minimo).

Riso. 1.
Viene mostrato il grafico di una funzione che ha due punti massimi ( X 1 e X 3) e due punti minimi ( X 2 e X 4), e il valore massimo può essere inferiore al minimo ( ƒ (X 1 ) < ƒ (X 4)). Ciò sottolinea il fatto che caratterizziamo la singolarità di una funzione solo vicino a un certo punto.
I valori della funzione nei punti di massimo e minimo sono chiamati valori estremi o estremi. Il grafico sopra mostra che i punti estremi ( X 1 , X 2 , X 3 , X 4) determinare gli intervalli di monotonicità della funzione, in ciascuno dei quali la derivata conserva un certo segno. Nei punti estremi, ovviamente, la derivata va a zero. Formuliamo un teorema su condizione necessaria esistenza di un estremo.
Teorema. Se la funzione ƒ (X) al punto X 0 ha un estremo, allora la derivata della funzione a questo punto è uguale a zero, cioè ƒ¢ ( X 0)=0.
Notiamo subito che questa condizione non è sufficiente, cioè non sempre è vera l'affermazione contraria. Dall'uguaglianza ƒ ¢ ( X 0)= 0 non significa necessariamente questo in quel momento X 0 c'è un estremo.
Ciò è confermato da un esempio con la funzione ƒ (X)=x 3 .
Lo troveremo ƒ ¢ ( X)= 3X 2 . Al punto X=0 ƒ ¢ (0)=0 . Ma quanto vuoi vicino al punto X=0 troveremo X> 0, dove ƒ (X)=x 3 > 0, troveremo X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, dove per tutti X valore della funzione in un punto X=0 sarà il più grande o il più piccolo. Quindi punto X=0 non è un punto estremo.
Si può discutere diversamente. Poiché la derivata ƒ ¢ (x)=3x 2 , quindi la funzione ƒ(x)=x 3 aumenta per ogni x reale e non ha estremi.
Punti in cui è soddisfatta la condizione estrema necessaria (ƒ ¢ (x)=0) sono chiamati critico .
Ovviamente la tangente al grafico della funzione nei punti in cui ƒ ¢ (x)=0, parallelo all'asse x Ox .
Condizione sufficiente l'estremo è dato nei seguenti teoremi.
Teorema 1. Se X 0 è il punto critico della funzione e passando per esso la derivata cambia segno, quindi X 0 è un punto estremo, cioè se la derivata cambia segno da più a meno è un punto di massimo, se cambia segno da meno a più è un punto di minimo.
Si noti che non c'è estremo in un punto se la derivata non cambia segno. La regola per studiare l'estremo utilizzando la derivata prima è nota dal corso scolastico. A volte è più conveniente formulare una condizione sufficiente per un estremo utilizzando la derivata seconda.
Sia la funzione ƒ( X) è due volte differenziabile in qualche dominio (cioè ƒ( X) ha ƒ¢ ( X) E ƒ ¢¢ ( X)).
Teorema 2. Se X 0 – punto critico della funzione ƒ(x) e ƒ ¢¢ (X 0 ) > 0 , Quello X 0 – punto minimo, se ƒ ¢¢ (X 0 ) < 0, то X 0 – punto massimo.
Utilizzando la derivata seconda si determina la convessità o concavità del grafico di una funzione.
Convessità, concavità. Punto di flesso.
Curva y=ƒ(X) è chiamato convessoth sotto qualcuno di lei tangente
ƒ ¢¢ ( X) < 0.
Curva y=ƒ(X) è chiamato concavo su un intervallo se tutti i punti della curva giacciono più alto qualcuno di lei tangente su questo intervallo. Quindi in questo intervallo
ƒ ¢¢(x) > 0
Definizione. Punto di flesso Una curva è un punto in cui da un lato la curva è convessa e dall'altro è concava.
Al punto di flesso ƒ ¢¢ ( X)=0.
Quindi, il segno della derivata seconda (così come il segno della funzione stessa e della sua derivata prima) indica le caratteristiche del grafico della funzione. Guardiamoli di nuovo.
Se per tutti X nell'intervallo ( UN, B) ƒ (X) > 0 (ƒ (X) < 0), il grafico si trova sopra (sotto) l'asse x.
Se per tutti X nell'intervallo ( UN, B) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (UN, B) aumenta (diminuisce).
Se per tutti X nell'intervallo ( UN, B) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (UN, B) concavo (convesso).
Equazione ƒ( X)=0 definisce gli “zeri” della funzione, cioè i punti di intersezione del grafico con l'asse Ox.
L'equazione ƒ ¢ ( X)=0 definisce i punti critici.
L'equazione ƒ ¢¢ ( X)=0 definisce i possibili punti di flesso.
Schema di studio delle funzioni
Studiare la funzione ƒ (X) e tracciando y=ƒ(X) si dovrebbe trovare:
1) il dominio di definizione della funzione e il punto di intersezione del grafico con gli assi coordinati;
2) intervalli di monotonia;
3) punti estremi e valori di funzione in questi punti;
4) intervalli di convessità e concavità del grafico;
5) punti di flesso del grafico;
6) costruire in un sistema di coordinate cartesiane tutti i punti ottenuti (a volte, per rendere più chiaro il grafico, si ottengono punti aggiuntivi) e il grafico stesso.
I valori più piccoli e più grandi di una funzione su un segmento
Quando si risolvono alcuni problemi del metodo di ottimizzazione, è importante riuscire a trovare i valori più piccoli o più grandi di una funzione su un determinato segmento. La funzione raggiunge questi valori o nei punti critici o alle estremità del segmento.
Schema di ricerca i valori più piccoli e più grandi della funzione ƒ (X) sul segmento [ UN, B].
1. Trova la derivata della funzione ƒ ¢ ( X).
2. Trova i punti critici dall'equazione ƒ ¢ ( X)=0.
3. Seleziona i punti critici che appartengono a questo segmento [ UN, B] e trova il valore della funzione ƒ (X) in ciascuno di questi punti.
4. Calcolare i valori delle funzioni ƒ (X) alle estremità del segmento: ƒ( UN) e ƒ( B).
5. Dai valori della funzione ottenuti, selezionare il più grande (il più grande) e il più piccolo (il più piccolo).
Esempio 2.
Trova i valori più grandi e più piccoli di una funzione ƒ(x)=X 3 –9x 2 +24х–10 sul segmento.
1. ƒ ¢ ( X)= 3X 2 – 9·2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. Il punto x 2 =4 non appartiene al segmento. Pertanto, calcoliamo il valore della funzione solo nel punto X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Valori delle funzioni alle estremità del segmento: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Valori ottenuti:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Il valore più alto è 10 e viene raggiunto nel punto X=2. Il più piccolo è pari a –10 e si ottiene al punto X=0.
Esempio 3.
Trova gli intervalli di convessità e concavità e i punti di flesso della curva y=x+36X 2 –2X 3 –X 4 .
Il dominio di definizione di questa funzione è l'insieme di tutti i numeri reali, cioè XЄ(–∞, +∞).
Troviamo la derivata seconda.
A¢ =1+72 X–6X 2 –4X 3 .
A¢¢ =72–12 X–12X 2 = –12(X 2 +X–6).
Dall'Eq. A¢¢ =0 si ottiene l'ascissa del punto di flesso:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
Definiamo il segno A¢¢ sugli intervalli
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
A¢¢
forma della curva
convesso
inflessione
concavo
inflessione
convesso
Troviamo le ordinate dei punti di flesso:
A(–3)=726; M 1 (–3; 726) – punto di flesso
A(2)=114; M 2 (2; 114) – punto di flesso.
Nell'intervallo (–3; 2) la curva è concava. Negli intervalli (–∞; –3) e (2; +∞) – convesso.
Esempi di incarichi
Compito n. 1.
Trova i punti di interruzione della funzione e traccia il grafico

Funzione ƒ (X) è definito per tutto reale X ed è continua su ciascuno degli intervalli indicati: (–∞; –1), [–1; 0], (0, +∞). Esploriamo la funzione ƒ (X) per la continuità nei punti X= –1 e X=0.
Per fare ciò, troveremo limiti unilaterali in ciascuno di questi punti.

Poiché i limiti unilaterali sono diversi, allora X = –1 – punto di discontinuità del primo tipo.
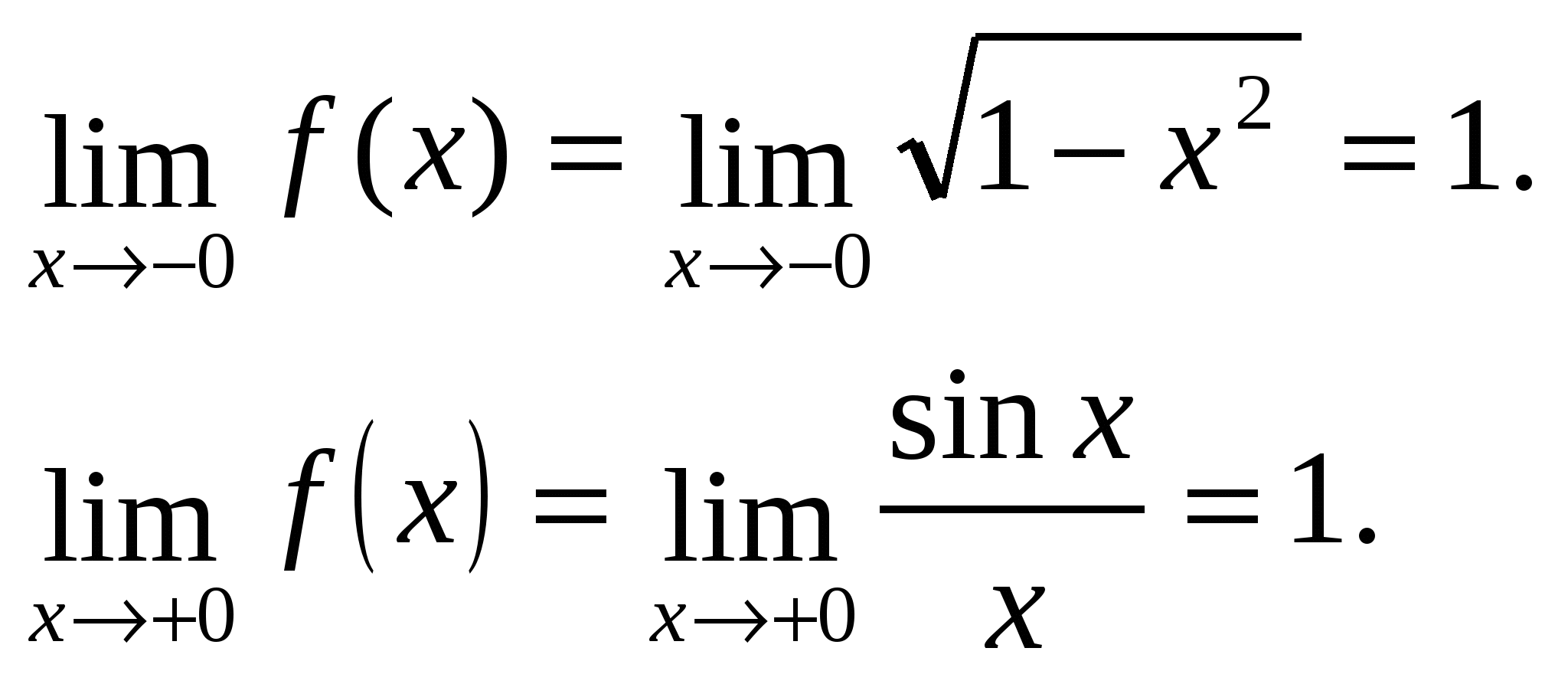
I limiti unilaterali sono uguali, cioè nel punto x=0 c'è un limite della funzione e 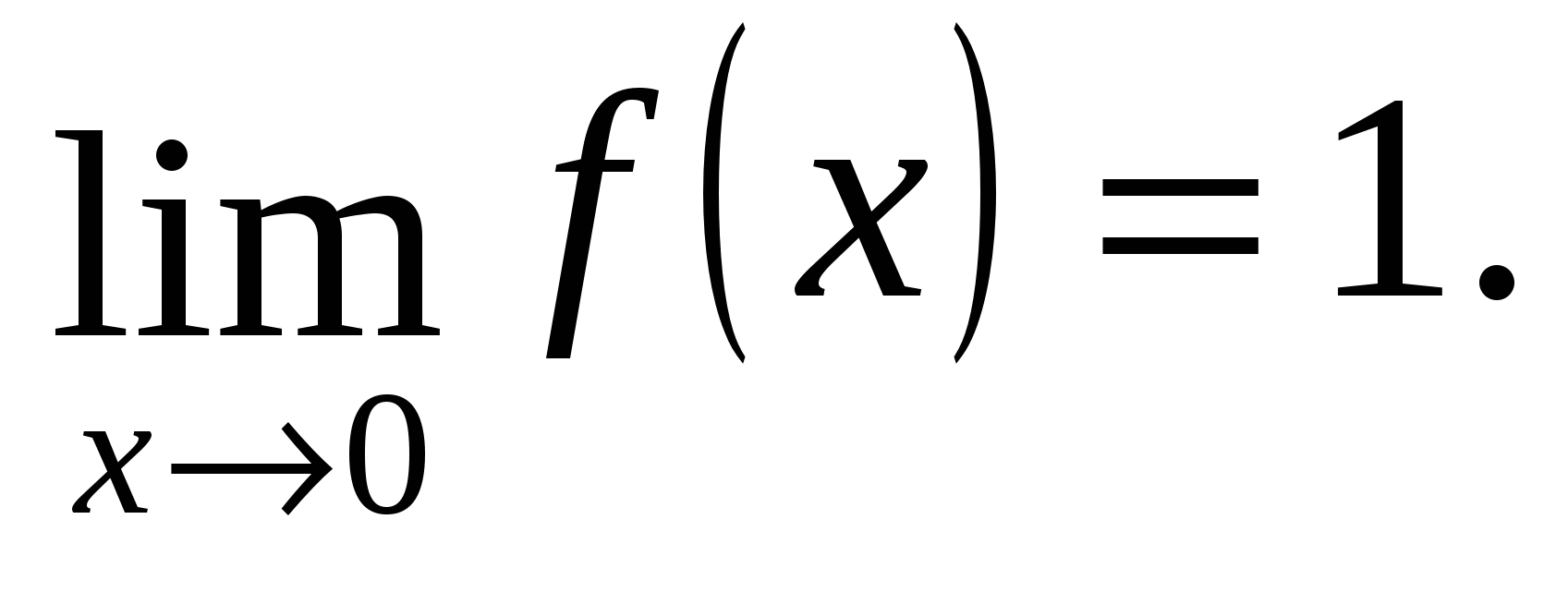
Confrontiamo questo limite con il valore della funzione nel punto: 
Perché  poi dentro per x=0 la funzione ƒ(x) è continua.
poi dentro per x=0 la funzione ƒ(x) è continua.
Tracciamo la funzione ƒ (X), dato che
1)  – equazione di una retta,
– equazione di una retta,
2)  – equazione del semicerchio superiore
– equazione del semicerchio superiore  con centro nell'origine e raggio pari all'unità, e sotto la condizione –1 £ X£ 0 equazione
con centro nell'origine e raggio pari all'unità, e sotto la condizione –1 £ X£ 0 equazione  definisce un quarto di cerchio.
definisce un quarto di cerchio.
3) per X > 0 il grafico è dato dall'equazione  . Troviamo i punti di intersezione di questa curva con l'asse del bue dall'equazione
. Troviamo i punti di intersezione di questa curva con l'asse del bue dall'equazione 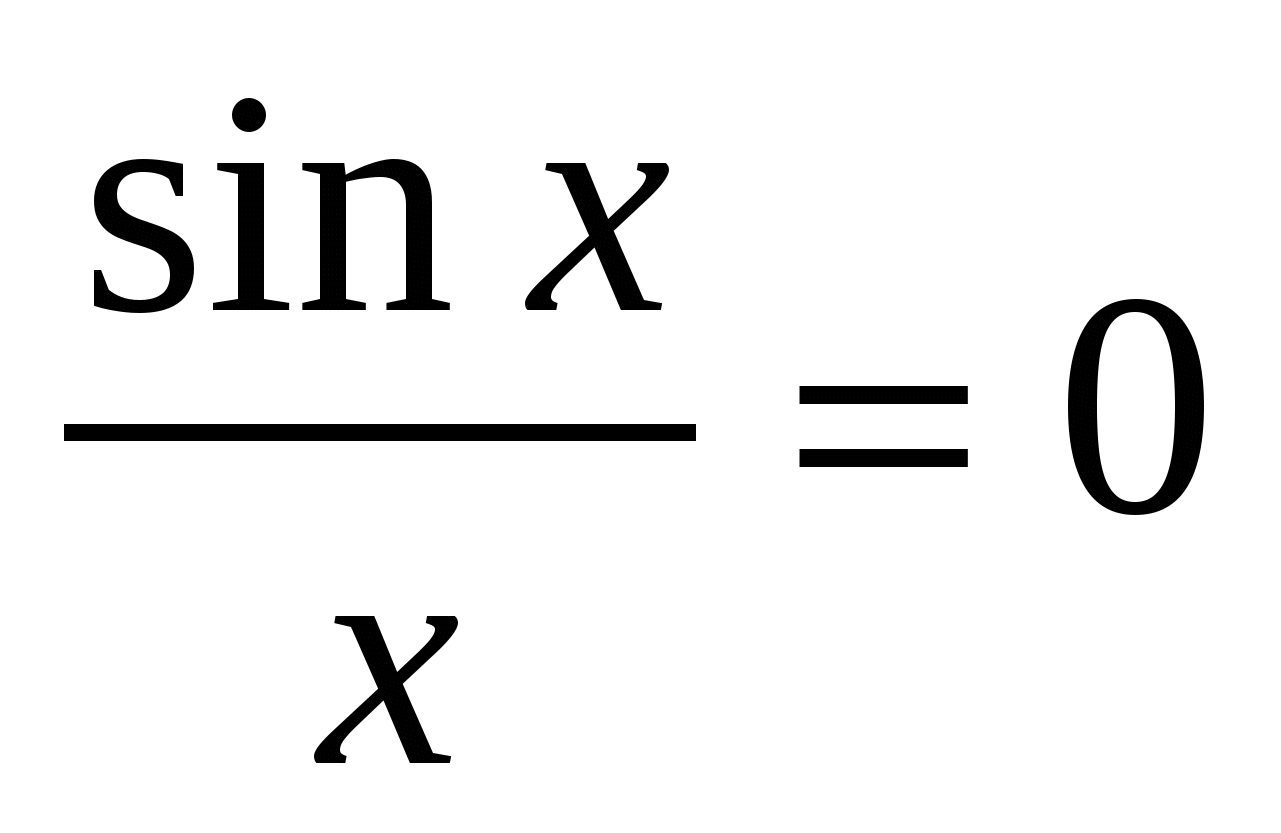 per x > 0. x= π
N, Dove N
=1, 2, 3, 4,
per x > 0. x= π
N, Dove N
=1, 2, 3, 4,

Riso. 2.
Compito n. 2.
Scrivi le equazioni per le tangenti a una retta  nei punti dove X=0 e X=4. Trova il punto di intersezione delle tangenti e l'angolo compreso tra loro. Fai un disegno.
nei punti dove X=0 e X=4. Trova il punto di intersezione delle tangenti e l'angolo compreso tra loro. Fai un disegno.
Equazione della tangente ad una retta y=ƒ(x) sembra
Dove A 0 =ƒ( X 0).
Al punto X=0 A(0)=ƒ(0)=5.
A¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
M 1 (0, 5) ha la forma sì– 5= –3(X–0) o
y= –3X+5.
Al punto X=4 A(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Equazione di una tangente in un punto M 2 (4, 1) ha la forma sì– 1=X–4 o
y=x–3.
Otteniamo il punto di intersezione delle tangenti risolvendo il sistema

Punto di intersezione M 3 (2, –1).
Angolo φ tra le tangenti troviamo dalla formula:
 ,
,
Dove K 1 = –3; K 2 =1 – coefficienti angolari delle tangenti.
 .
.
Angolo φ =arctg 2.
Costruiamo questa linea  – una parabola con vertice nel punto dove X=3, perché A¢
=0 a X=3. Lo troveremo
– una parabola con vertice nel punto dove X=3, perché A¢
=0 a X=3. Lo troveremo  . Punto M 4 (3;
. Punto M 4 (3;  ) è il vertice della parabola.
) è il vertice della parabola.
R 
È. 3.
Compito n.3.
Esplora la funzione 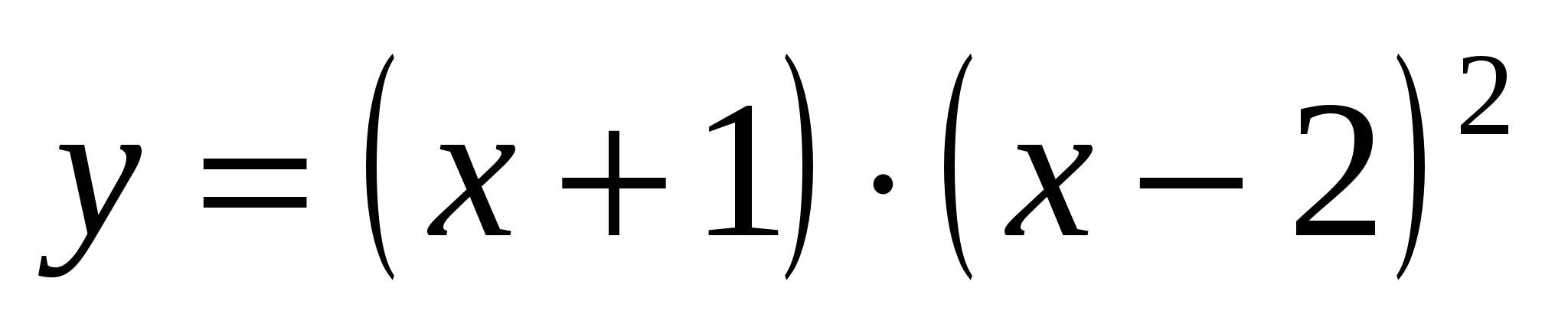 e tracciarlo.
e tracciarlo.
1. Questa funzione è un polinomio (apriamo le parentesi, otteniamo un polinomio di terzo grado), quindi è definita, continua e differenziabile per qualsiasi X.
2. Troviamo la derivata.
 .
.
Dall'Eq. A¢ =0 troviamo i punti critici: 3 X·( X–2)=0, X 1 =0, X 2 =2.
Esploriamoli.
X
(–∞, 0)
(0; 2)
(2; +∞)
A ¢
A
3. Quindi, la funzione aumenta sugli intervalli (–∞, 0) e (2, +∞), diminuisce sull'intervallo (0; 2), ha un massimo in x=0 e un minimo in x=2:
A massimo = A(0)=4; A minimo = A(2)=0.
4. Troviamo la derivata seconda.
A¢¢ = 6·( X-1).
La curva è convessa dove A¢¢ < 0, т. е. 6·(X–1) < 0, X < 1.
La curva è concava dove A¢¢ > 0, cioè X > 1.
Quindi, sull'intervallo (–∞, 1) la curva è convessa; e sull'intervallo (1, +∞) è concavo.
5. Troviamo il punto di flesso dall'equazione A¢¢ =0. Così, X=1 – ascissa del punto di flesso, perché questo punto separa gli intervalli di convessità e concavità della curva. Ordinata del punto di flesso: A(1)=2.
Grafico di una funzione A=(X+1)·( X–2) 2 interseca l'asse del bue in A=0, cioè quando X= –1 e X=2;
attraversa l'asse Oy a X=0, cioè quando A=4. Abbiamo ottenuto tre punti: (–1; 0), (2; 0), (0; 4). Inseriremo nella tabella tutti i punti ottenuti, sommando quelli ad essi adiacenti.
–2
–1



–16


È. 4 Curva y=(x+1)(x–2) 2.
Compito n. 1
Ti presentiamo compiti che possono avere una, due, tre o più risposte corrette. Cerchia i numeri di tutte le risposte corrette.
1. Se  poi la funzione
poi la funzione
1) crescente
2) decrescente
3) costante
2. Se
1) In aumento
2) Diminuendo
3. Se  , quindi la funzione
, quindi la funzione
1) In aumento
2) Diminuendo
4. Se  , quindi la funzione
, quindi la funzione
1) In aumento 3) In diminuzione
2) Costante 4) Monotono
5. Funzione  È
È
1) Pari
2) Nemmeno
3) né pari né dispari
4) Periodico
5) Non periodico
6) Trigonometrico
7) Elementare
6. Funzione  È
È
1) pari
2) strano
3) né pari né dispari
4) periodico
5) non periodico
6) trigonometrico
7) elementare
2) Weierstrass 4) Dirichlet 6) Leibniz
8) Soluzione  Equazioni
Equazioni
1) 0 3) 0 e 3 5) 2 7) 3
2) 2 e 3 4) 2 6) -5 e 1 8) 5 e 1
9) soluzione alla disuguaglianza 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 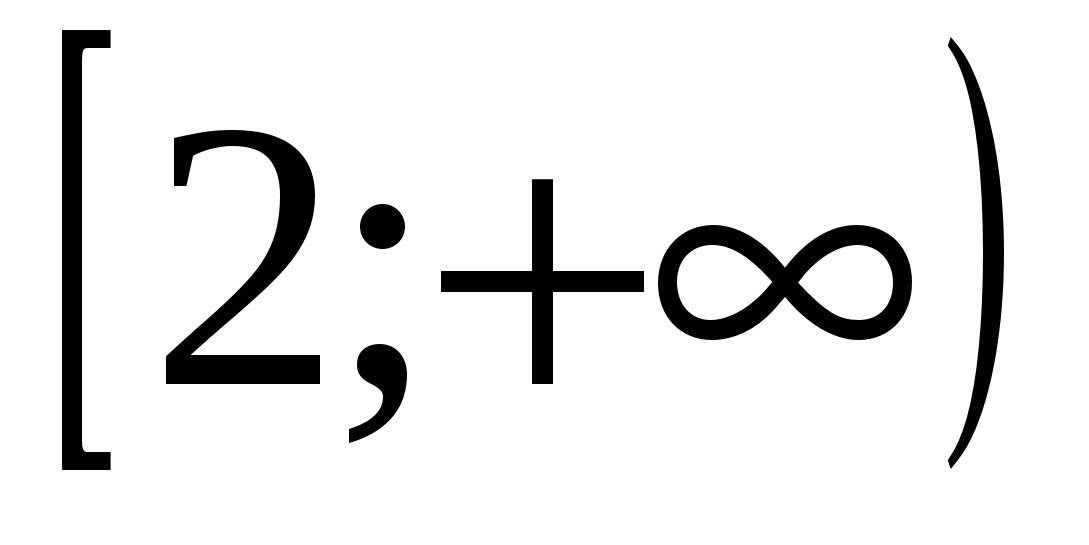
10) Metodo  L'importo è stato trovato
L'importo è stato trovato
1) vettori
2) dritto
3) segmento
11) Se  , quindi la funzione
, quindi la funzione
1) Concavo 3) Convesso 5) Decrescente
2) Monotonico 4) Crescente 6) Costante
12) il dominio di definizione della funzione è pari a 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 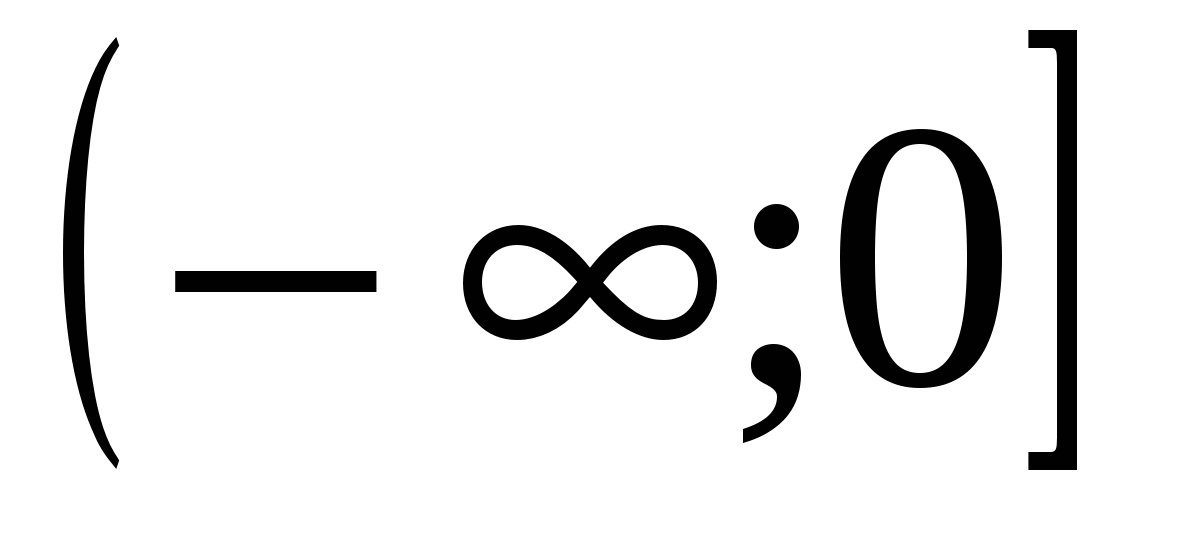
7) (-1;1)
8) 
9) 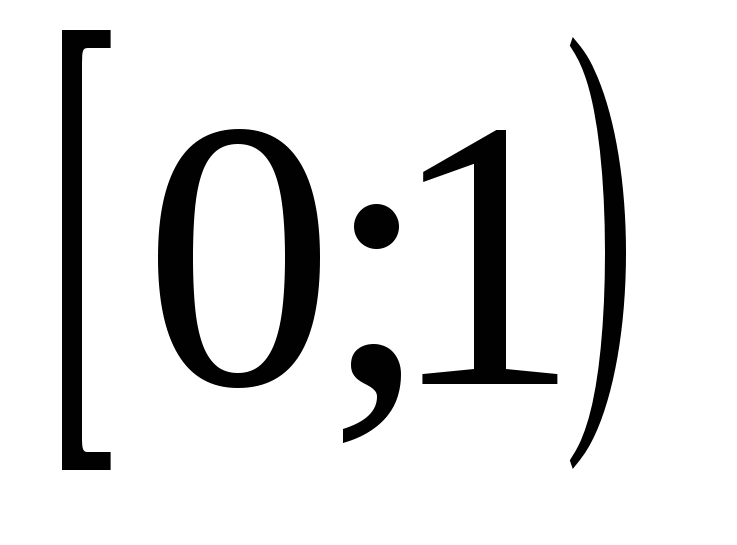
13) funzione  È
È
1) indicativo
2) trigonometrico
3) potere
4) logaritmico
14) se funzioni y = X  allora lo è
allora lo è 
1) pari
2) strano
3) né pari né dispari
15) funzione  A
A  È
È

 .
.


