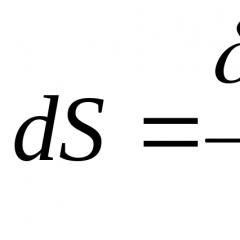Lezione "segmenti proporzionali in un triangolo rettangolo". Lezione "segmenti proporzionali in un triangolo rettangolo" Formule per i segmenti proporzionali in un triangolo rettangolo

Obiettivi della lezione:

1. introdurre il concetto di media proporzionale (media geometrica) di due segmenti;
2. considerare il problema dei segmenti proporzionali in triangolo rettangolo: proprietà dell'altezza di un triangolo rettangolo tracciato dal vertice di un angolo retto;
3. sviluppare le capacità degli studenti nell'utilizzo dell'argomento studiato nel processo di risoluzione dei problemi.

Tipo di lezione: lezione di apprendimento di nuovo materiale.

Piano:

1. Momento dell'organizzazione.
2. Aggiornamento della conoscenza.
3. Studiando la proprietà dell'altezza di un triangolo rettangolo disegnato dal vertice di un angolo retto:
   – fase preparatoria;
   – introduzione;
   – assimilazione.
4. Introduzione del concetto di media proporzionale a due segmenti.
5. Padroneggiare il concetto di media proporzionale di due segmenti.
6. Prova delle conseguenze:
   – l'altezza di un triangolo rettangolo tracciato dal vertice di un angolo retto è la media proporzionale tra i segmenti in cui è divisa l'ipotenusa da tale altezza;
   – il cateto di un triangolo rettangolo è la media proporzionale tra l'ipotenusa e il segmento di ipotenusa compreso tra il cateto e l'altezza.
7. Risoluzione dei problemi.
8. Riassumendo.
9. Impostazione dei compiti.

Avanzamento della lezione

I. MOMENTO ORGANIZZATIVO

- Ciao ragazzi, accomodatevi. Sono tutti pronti per la lezione?

Cominciamo a lavorare.

II. CONOSCENZA AGGIORNATA

– Quale importante concetto matematico hai imparato nelle lezioni precedenti? ( con il concetto di somiglianza dei triangoli)

- Ricordiamo quali due triangoli si chiamano simili? (due triangoli si dicono simili se i loro angoli sono rispettivamente uguali e i lati di un triangolo sono proporzionali ai lati simili dell'altro triangolo)

– Cosa usiamo per dimostrare la somiglianza di due triangoli? (

– Formulare questi segni (formulare tre segni di somiglianza dei triangoli)

III. STUDIO DELLE PROPRIETÀ DELL'ALTEZZA DI UN TRIANGOLO RETTANGOLARE, CONDOTTO DALLA SUPERIORE DI UN ANGOLO RETTO

a) fase preparatoria

– Ragazzi, guardate la prima diapositiva. ( Applicazione) Qui sono mostrati due triangoli rettangoli – e . e sono le altezze e rispettivamente. .

Compito 1.a) Determina se e sono simili.

– Cosa usiamo per dimostrare la somiglianza dei triangoli? ( segni di somiglianza dei triangoli)

(il primo segno, perché nel problema non si sa nulla dei lati dei triangoli)

. (Due coppie: 1. ∟B= ∟B1 (dritto), 2. ∟A= ∟A 1)

– Trarre una conclusione.( dal primo criterio di somiglianza dei triangoli ~)

Compito 1.b) Determina se e sono simili.

– Quale segno di somiglianza utilizzeremo e perché? (il primo segno, perché nel problema non si sa nulla dei lati dei triangoli)

– Quante paia angoli uguali dobbiamo trovare? Trova queste coppie (poiché i triangoli sono rettangoli, allora è sufficiente una coppia di angoli uguali: ∟A= ∟A 1)

- Trarre una conclusione. (sulla base del primo criterio di somiglianza dei triangoli, concludiamo che questi triangoli sono simili).

Come risultato della conversazione, la diapositiva 1 appare così:

b) scoperta del teorema

Compito 2.

– Determinare se e sono simili. Come risultato della conversazione, vengono costruite risposte che si riflettono sulla diapositiva.

– L'immagine indicava che. Abbiamo utilizzato questa misura di laurea quando abbiamo risposto alle domande sui compiti? ( No, non l'abbiamo usato)

– Ragazzi, traete una conclusione: in quali triangoli si divide un triangolo rettangolo per l'altezza tracciata dal vertice dell'angolo retto? (concludere)

– La domanda sorge spontanea: questi due triangoli rettangoli, in cui l’altezza divide il triangolo rettangolo, saranno simili tra loro? Proviamo a trovare coppie di angoli uguali.

Come risultato della conversazione, viene creato un record:

– Ora traiamo una conclusione completa.( CONCLUSIONE: l'altezza di un triangolo rettangolo disegnato dal vertice dell'angolo retto divide il triangolo in due simile

- Quello. Abbiamo formulato e dimostrato un teorema sulla proprietà dell'altezza di un triangolo rettangolo.

Stabiliamo la struttura del teorema e facciamo un disegno. Cosa c'è nel teorema e cosa deve essere dimostrato? Gli studenti scrivono sul loro quaderno:

– Dimostriamo il primo punto del teorema per il nuovo disegno. Quale caratteristica di somiglianza utilizzeremo e perché? (Il primo, perché nel teorema non si sa nulla dei lati dei triangoli)

– Quante coppie di angoli uguali dobbiamo trovare? Trova queste coppie. (IN in questo casoè sufficiente una coppia: ∟A-generale)

- Trarre una conclusione. I triangoli sono simili. Di conseguenza, viene mostrato un esempio del teorema

– Scrivi tu stesso il secondo e il terzo punto a casa.

c) padroneggiare il teorema

- Quindi, formula di nuovo il teorema (L'altezza di un triangolo rettangolo tracciato dal vertice di un angolo retto divide il triangolo in due simile triangoli rettangoli, ognuno dei quali è simile a questo)

– Quante paia triangoli simili nella costruzione “in un triangolo rettangolo l'altezza si traccia dal vertice di un angolo retto”, questo teorema ti permette di trovare? ( Tre paia)

Agli studenti viene assegnato il seguente compito:

IV. INTRODUZIONE DEL CONCETTO DI MEDIA PROPORZIONALE DI DUE SEGMENTI

– E ora studieremo con te un nuovo concetto.

Attenzione!

Definizione. Segmento XY chiamato medio proporzionale (media geometrica) tra i segmenti AB E CD, Se

(scrivilo su un quaderno).

V. COMPRENSIONE DEL CONCETTO DI MEDIA PROPORZIONALE DI DUE SEGMENTI

– Ora passiamo alla diapositiva successiva.

Compito 1. Trova la lunghezza dei segmenti proporzionali medi MN e KP, se MN = 9 cm, KP = 16 cm.

– Cosa c’è nel problema? ( Due segmenti e le loro lunghezze: MN = 9 cm, KP = 16 cm)

– Cosa devi trovare? ( La lunghezza della media proporzionale a questi segmenti)

– Quale formula esprime la media proporzionale e come la troviamo?

(Sostituisci i dati nella formula e trova la lunghezza del sostegno medio.)

Compito n. 2. Trova la lunghezza del segmento AB se la media proporzionale dei segmenti AB e CD è 90 cm e CD = 100 cm

– Cosa c’è nel problema? (la lunghezza del segmento CD = 100 cm e la media proporzionale dei segmenti AB e CD è 90 cm)

– Cosa si dovrebbe trovare nel problema? ( Lunghezza del segmento AB)

– Come risolveremo il problema? (Scriviamo la formula per i segmenti proporzionali medi AB e CD, esprimiamo la lunghezza AB da essa e sostituiamo i dati nel problema.)

VI. CONCLUSIONE DELLE IMPLICAZIONI

- Ben fatto, ragazzi. Ora torniamo alla somiglianza dei triangoli, che abbiamo dimostrato nel teorema. Enuncia nuovamente il teorema. ( L'altezza di un triangolo rettangolo tracciato dal vertice di un angolo retto divide il triangolo in due simile triangoli rettangoli, ognuno dei quali è simile a quello dato)

– Usiamo prima la somiglianza dei triangoli e . Cosa ne consegue? ( Per definizione, i lati di somiglianza sono proporzionali ai lati simili)

– Quale uguaglianza risulterà utilizzando la proprietà fondamentale della proporzione? ()

– Esprimere CD e trarre una conclusione (;.

Conclusione: l'altezza di un triangolo rettangolo tracciato dal vertice di un angolo retto è la media proporzionale tra i segmenti in cui è divisa l'ipotenusa da tale altezza)

– Ora prova tu stesso che il cateto di un triangolo rettangolo è il medio proporzionale tra l'ipotenusa e il segmento dell'ipotenusa racchiuso tra il cateto e l'altezza Troveremo da -... i segmenti in cui è divisa l'ipotenusa da questa altitudine )

Un cateto di un triangolo rettangolo è il medio proporzionale tra...(-...l'ipotenusa e il segmento di ipotenusa racchiuso tra questo cateto e l'altezza )

– Dove applichiamo le affermazioni che abbiamo imparato? ( Quando si risolvono i problemi)

IX. IMPOSTAZIONE DEI COMPITI

d/z: N. 571, N. 572 (a, d), lavoro indipendente in un taccuino, teoria.

Lezione 40. Segmenti proporzionali in un triangolo rettangolo. C.b. UN. H. S. aC. N. ac. A. B. L'altezza di un triangolo rettangolo tracciato dal vertice di un angolo retto divide il triangolo in 2 triangoli rettangoli simili, ciascuno dei quali è simile al triangolo dato. Test per la somiglianza dei triangoli rettangoli. Due triangoli rettangoli sono simili se hanno ciascuno un angolo acuto uguale. Il segmento XY è chiamato media proporzionale (media geometrica) per i segmenti AB e CD se Proprietà 1. L'altezza di un triangolo rettangolo tracciato dal vertice dell'angolo retto è la media proporzionale tra le proiezioni dei cateti sull'ipotenusa. Proprietà 2. Un cateto di un triangolo rettangolo è il medio proporzionale tra l'ipotenusa e la proiezione di questo cateto sull'ipotenusa.

La dimensione dell'archivio con la presentazione è di 232 KB.

altre presentazioni "Risoluzione dei problemi sul teorema di Pitagora" - Il triangolo ABC è isoscele. Applicazione pratica Teorema di Pitagora. ABCD è un quadrilatero. Area di un quadrato. Trova il sole. Prova. Basi di un trapezio isoscele. Consideriamo il teorema di Pitagora. Area di un quadrilatero. Triangoli rettangoli. Teorema di Pitagora. Quadrato dell'ipotenusa pari alla somma

quadrati di gambe.

"Trovare l'area di un parallelogramma" - Base. Altezza. Determinazione dell'altezza di un parallelogramma. Segni di uguaglianza dei triangoli rettangoli. Area di un parallelogramma. Trova l'area del triangolo. Proprietà delle aree. Esercizi orali. Trova l'area del parallelogramma. Altezze di un parallelogramma. Trova il perimetro del quadrato. Area di un triangolo. Trova l'area del quadrato. Trova l'area del rettangolo. Area di un quadrato.

“Definizione di simmetria assiale” - Punti che giacciono sulla stessa perpendicolare. Disegna due linee rette. Costruzione. Traccia i punti. Traccia. Figure che non hanno simmetria assiale. Segmento. Coordinate mancanti. Figura. Figure che hanno più di due assi di simmetria. Simmetria. Simmetria nella poesia. Costruisci triangoli. Assi di simmetria. Costruzione di un segmento. Costruzione di un punto. Figure con due assi di simmetria. Popoli. Triangoli. Proporzionalità.

“Definizione di triangoli simili” - Poligoni. Segmenti proporzionali. Rapporto tra le aree di triangoli simili. Due triangoli si dicono simili. Condizioni. Costruisci un triangolo utilizzando i due angoli indicati e la bisettrice al vertice. Diciamo che dobbiamo determinare la distanza dal pilastro. Il terzo segno di somiglianza dei triangoli. Costruiamo una specie di triangolo. ABC. I triangoli ABC e ABC sono uguali su tre lati. Determinazione dell'altezza di un oggetto.

"Soluzione del teorema di Pitagora" - Parti di finestre. La prova più semplice. Hammurabi. Diagonale. Prova completa. Dimostrazione mediante metodo di sottrazione. Pitagorici. Dimostrazione mediante metodo di scomposizione. Storia del teorema. Diametro. Dimostrazione con il metodo dell'addizione. La prova di Epstein. Cantore. Triangoli. Seguaci. Applicazioni del teorema di Pitagora. Teorema di Pitagora. Enunciato del teorema. La prova di Perigal. Applicazione del teorema.

Test di similarità per triangoli rettangoli

Introduciamo innanzitutto il criterio di similarità per i triangoli rettangoli.

Teorema 1

Test di similarità per triangoli rettangoli: due triangoli rettangoli sono simili quando hanno ciascuno un angolo acuto uguale (Fig. 1).

Figura 1. Triangoli rettangoli simili

Prova.

Sia dato che $\angolo B=\angolo B_1$. Poiché i triangoli sono rettangoli, allora $\angle A=\angle A_1=(90)^0$. Pertanto, sono simili secondo il primo criterio di somiglianza dei triangoli.

Il teorema è stato dimostrato.

Teorema dell'altezza nel triangolo rettangolo

Teorema 2

L'altezza di un triangolo rettangolo tracciato dal vertice di un angolo retto divide il triangolo in due triangoli rettangoli simili, ciascuno dei quali è simile al triangolo dato.

Prova.

Sia dato un triangolo rettangolo $ABC$ con angolo retto $C$. Disegniamo l'altezza $CD$ (Fig. 2).

Figura 2. Illustrazione del Teorema 2

Dimostriamo che i triangoli $ACD$ e $BCD$ sono simili al triangolo $ABC$ e che i triangoli $ACD$ e $BCD$ sono simili tra loro.

Poiché $\angolo ADC=(90)^0$, allora il triangolo $ACD$ è rettangolo. I triangoli $ACD$ e $ABC$ hanno un angolo comune $A$, quindi, per il Teorema 1, i triangoli $ACD$ e $ABC$ sono simili.

Poiché $\angolo BDC=(90)^0$, allora il triangolo $BCD$ è rettangolo. I triangoli $BCD$ e $ABC$ hanno un angolo comune $B$, quindi, per il Teorema 1, i triangoli $BCD$ e $ABC$ sono simili.

Consideriamo ora i triangoli $ACD$ e $BCD$

\[\angolo A=(90)^0-\angolo ACD\] \[\angolo BCD=(90)^0-\angolo ACD=\angolo A\]

Pertanto, per il Teorema 1, i triangoli $ACD$ e $BCD$ sono simili.

Il teorema è stato dimostrato.

Medio proporzionale

Teorema 3

L'altezza di un triangolo rettangolo tracciato dal vertice di un angolo retto è la media proporzionale ai segmenti in cui l'altezza divide l'ipotenusa del triangolo dato.

Prova.

Per il Teorema 2 abbiamo che i triangoli $ACD$ e $BCD$ sono quindi simili

Il teorema è stato dimostrato.

Teorema 4

Il cateto di un triangolo rettangolo è il medio proporzionale tra l'ipotenusa e il segmento di ipotenusa racchiuso tra il cateto e l'altezza ricavata dal vertice dell'angolo.

Prova.

Nella dimostrazione del teorema utilizzeremo la notazione della Figura 2.

Per il Teorema 2 abbiamo che i triangoli $ACD$ e $ABC$ sono quindi simili

Il teorema è stato dimostrato.

Oggi portiamo alla vostra attenzione un'altra presentazione su un argomento straordinario e misterioso: la geometria. In questa presentazione vi presenteremo un nuovo immobile forme geometriche, in particolare, con il concetto di segmenti proporzionali nei triangoli rettangoli.

Innanzitutto, dovremmo ricordare cos'è un triangolo? Questo è il poligono più semplice, costituito da tre vertici collegati da tre segmenti. Un triangolo è chiamato triangolo rettangolo in cui uno degli angoli è uguale a 90 gradi. Li avete già conosciuti in modo più dettagliato nel nostro precedente materiali didattici presentato alla tua attenzione.

Quindi, tornando al nostro argomento di oggi, denotiamo in ordine che l'altezza di un triangolo rettangolo disegnato da un angolo di 90 gradi lo divide in due triangoli simili sia tra loro che a quello originale. Tutti i disegni e i grafici che ti interessano sono riportati nella presentazione proposta, ti consigliamo di fare riferimento ad essi, accompagnati dalla spiegazione descritta;

Un esempio grafico della tesi di cui sopra può essere visto nella seconda diapositiva. In base al primo segno di somiglianza dei triangoli, i triangoli sono simili perché hanno due angoli identici. Se specifichiamo più in dettaglio, l'altezza abbassata all'ipotenusa forma con essa un angolo retto, cioè ci sono già angoli identici, e ciascuno degli angoli formati ha anche un angolo comune come quello originale. Il risultato sono due angoli uguali tra loro. Cioè, i triangoli sono simili.

Designiamo anche cosa significa il concetto di “media proporzionale” o “media geometrica”? Questo è un certo segmento XY per i segmenti AB e CD, quando è uguale radice quadrata prodotti delle loro lunghezze.

Da ciò segue anche che la gamba di un triangolo rettangolo è la media geometrica tra l'ipotenusa e la proiezione di questa gamba sull'ipotenusa, cioè un'altra gamba.

Un'altra proprietà del triangolo rettangolo è che la sua altezza, calcolata rispetto ad un angolo di 90°, è la media proporzionale tra le proiezioni dei cateti sull'ipotenusa. Se fai riferimento alla presentazione e agli altri materiali offerti alla tua attenzione, vedrai che c'è evidenza di questa tesi in una forma molto semplice e accessibile. In precedenza abbiamo già dimostrato che i triangoli risultanti sono simili tra loro e al triangolo originale. Quindi, utilizzando il rapporto tra le gambe di queste figure geometriche, arriviamo alla conclusione che l'altezza di un triangolo rettangolo è direttamente proporzionale alla radice quadrata del prodotto dei segmenti che si sono formati a seguito dell'abbassamento dell'altezza dal angolo retto del triangolo originale.

L'ultima cosa della presentazione è che il cateto di un triangolo rettangolo è la media geometrica dell'ipotenusa e del suo segmento situato tra il cateto e l'altezza tracciata da un angolo pari a 90 gradi. Questo caso dovrebbe essere considerato dal punto di vista che i triangoli indicati sono simili tra loro e la gamba di uno di essi risulta essere l'ipotenusa dell'altro. Ma ne acquisirai più familiarità studiando i materiali proposti.

Test di similarità per triangoli rettangoli

Introduciamo innanzitutto il criterio di similarità per i triangoli rettangoli.

Teorema 1

Test di similarità per triangoli rettangoli: due triangoli rettangoli sono simili quando hanno ciascuno un angolo acuto uguale (Fig. 1).

Figura 1. Triangoli rettangoli simili

Prova.

Sia dato che $\angolo B=\angolo B_1$. Poiché i triangoli sono rettangoli, allora $\angle A=\angle A_1=(90)^0$. Pertanto, sono simili secondo il primo criterio di somiglianza dei triangoli.

Il teorema è stato dimostrato.

Teorema dell'altezza nel triangolo rettangolo

Teorema 2

L'altezza di un triangolo rettangolo tracciato dal vertice di un angolo retto divide il triangolo in due triangoli rettangoli simili, ciascuno dei quali è simile al triangolo dato.

Prova.

Sia dato un triangolo rettangolo $ABC$ con angolo retto $C$. Disegniamo l'altezza $CD$ (Fig. 2).

Figura 2. Illustrazione del Teorema 2

Dimostriamo che i triangoli $ACD$ e $BCD$ sono simili al triangolo $ABC$ e che i triangoli $ACD$ e $BCD$ sono simili tra loro.

Poiché $\angolo ADC=(90)^0$, allora il triangolo $ACD$ è rettangolo. I triangoli $ACD$ e $ABC$ hanno un angolo comune $A$, quindi, per il Teorema 1, i triangoli $ACD$ e $ABC$ sono simili.

Poiché $\angolo BDC=(90)^0$, allora il triangolo $BCD$ è rettangolo. I triangoli $BCD$ e $ABC$ hanno un angolo comune $B$, quindi, per il Teorema 1, i triangoli $BCD$ e $ABC$ sono simili.

Consideriamo ora i triangoli $ACD$ e $BCD$

\[\angolo A=(90)^0-\angolo ACD\] \[\angolo BCD=(90)^0-\angolo ACD=\angolo A\]

Pertanto, per il Teorema 1, i triangoli $ACD$ e $BCD$ sono simili.

Il teorema è stato dimostrato.

Medio proporzionale

Teorema 3

L'altezza di un triangolo rettangolo tracciato dal vertice di un angolo retto è la media proporzionale ai segmenti in cui l'altezza divide l'ipotenusa del triangolo dato.

Prova.

Per il Teorema 2 abbiamo che i triangoli $ACD$ e $BCD$ sono quindi simili

Il teorema è stato dimostrato.

Teorema 4

Il cateto di un triangolo rettangolo è il medio proporzionale tra l'ipotenusa e il segmento di ipotenusa racchiuso tra il cateto e l'altezza ricavata dal vertice dell'angolo.

Prova.

Nella dimostrazione del teorema utilizzeremo la notazione della Figura 2.

Per il Teorema 2 abbiamo che i triangoli $ACD$ e $ABC$ sono quindi simili

Il teorema è stato dimostrato.