Cos'è un'equazione?

Coloro che stanno muovendo i primi passi nell'algebra, ovviamente, richiedono la presentazione più ordinata del materiale. Pertanto, nel nostro articolo su cos'è un'equazione, non solo daremo una definizione, ma forniremo anche varie classificazioni di equazioni con esempi.

Cos'è un'equazione: concetti generali

Quindi, un'equazione è un tipo di uguaglianza con un'incognita, denotata da una lettera latina. In questo caso il valore numerico di questa lettera, che ci permette di ottenere l'uguaglianza corretta, è chiamato radice dell'equazione, di cui potrete leggere di più nel nostro articolo, ma continueremo a parlare delle equazioni stesse. Gli argomenti di un'equazione (o variabili) sono incognite e la soluzione di un'equazione è trovare tutte le sue radici o l'assenza di radici.

Tipi di equazioni

Le equazioni si dividono in due grandi gruppi: algebriche e trascendenti.

• Un'equazione algebrica è quella in cui vengono utilizzate solo operazioni algebriche per trovare la radice dell'equazione - 4 operazioni aritmetiche, nonché l'elevamento a potenza e l'estrazione della radice naturale.
• Un'equazione trascendente è un'equazione in cui vengono utilizzate funzioni non algebriche per trovare la radice: ad esempio trigonometrica, logaritmica e altre.

Tra le equazioni algebriche ci sono anche:

• numeri interi - con entrambe le parti costituite da intere espressioni algebriche in relazione a incognite;
• frazionario - contenente espressioni algebriche intere al numeratore e al denominatore;
• irrazionale: le espressioni algebriche qui sono sotto il segno della radice.

Si noti inoltre che le equazioni frazionarie e irrazionali possono essere ridotte alla risoluzione di intere equazioni.

Le equazioni trascendentali si dividono in:

• Le equazioni esponenziali sono equazioni che contengono una variabile come esponente. Si risolvono spostandosi su una singola base o esponente, togliendo il fattore comune dalle parentesi, facendo la fattorizzazione e alcuni altri metodi;
• logaritmico - equazioni con logaritmi, cioè equazioni in cui le incognite sono all'interno dei logaritmi stessi. Risolvere tali equazioni è molto difficile (a differenza, ad esempio, della maggior parte di quelle algebriche), poiché richiede una solida formazione matematica. La cosa più importante qui è passare da un'equazione con logaritmi a un'equazione senza di essi, cioè semplificare l'equazione (questo metodo per rimuovere i logaritmi è chiamato potenziamento). Naturalmente è possibile potenziare un'equazione logaritmica solo se hanno basi numeriche identiche e non hanno coefficienti;
• le equazioni trigonometriche sono equazioni con variabili sotto i segni delle funzioni trigonometriche. La loro soluzione richiede la padronanza iniziale delle funzioni trigonometriche;
• miste sono equazioni differenziate con parti appartenenti a tipi diversi (ad esempio con parti paraboliche ed ellittiche oppure ellittiche e iperboliche, ecc.).

Per quanto riguarda la classificazione in base al numero di incognite, tutto è semplice: si distinguono equazioni con una, due, tre e così via. Esiste anche un'altra classificazione, che si basa sul grado che si trova sul lato sinistro del polinomio. Sulla base di ciò, si distinguono equazioni lineari, quadratiche e cubiche. Le equazioni lineari possono anche essere chiamate equazioni di 1o grado, quadratiche - 2o e cubiche, rispettivamente, 3o. Bene, ora diamo esempi di equazioni di un gruppo o di un altro.

Esempi di diversi tipi di equazioni

Esempi di equazioni algebriche:

• ax + b= 0
• ax 3 + bx 2 + cx+ d= 0
• ax 4 + bx 3 + cx 2 + bx + a= 0
  (a non è uguale a 0)

Esempi di equazioni trascendenti:

• cos x = x log x = x−5 2 x = logx+x 5 +40

Esempi di equazioni intere:

• (2+x)2 = (2+x)(55x-4) (x2-12x+10)4 = (3x+10)4 (4x2+3x-10)2=9x4

Esempio di equazioni frazionarie:

• 15 x + — = 5 x - 17 x

Esempio di equazioni irrazionali:

• √2kf(x)=g(x)

Esempi di equazioni lineari:

• 2x+7=0x - 3 = 2 - 4x 2x+3=5x+5 - 3x - 2

Esempi di equazioni quadratiche:

• x 2 +5x−7= 0 3x 2 +5x−7= 0 11x 2 −7x+3 = 0

Esempi di equazioni cubiche:

• x3 -9x2 -46x+120=0 x3 - 4x2 + x + 6 = 0

Esempi di equazioni esponenziali:

• 5 x+2 = 125 3 x 2 x = 8 x+3 3 2x +4 3 x -5 = 0

Esempi di equazioni logaritmiche:

• logaritmo 2 x= 3 logaritmo 3 x= -1

Esempi di equazioni trigonometriche:

• 3sen 2 x + 4sen x cosx + cos 2 x = 2 sin(5x+π/4) = ctg(2x-π/3) sinx + cos 2 x + tan 3 x = ctg 4 x

Esempi di equazioni miste:

• log x (log 9 (4⋅3 x −3))=1 |5x−8|+|2⋅5x+3|=13

Resta da aggiungere che vengono utilizzati una varietà di metodi per risolvere equazioni di vario tipo. Ebbene, per risolvere quasi tutte le equazioni, avrai bisogno di conoscenze non solo di algebra, ma anche di trigonometria e spesso di conoscenze molto approfondite.

Matematica. Algebra. Geometria. Trigonometria

ALGEBRA: Equazioni e sistemi di equazioni

4.2. Tipi di equazioni e metodi per risolverle

Nel caso in cui sia necessario trovare i valori di una variabile che soddisfino entrambe le equazioni date, diciamo che è data, sistema di equazioni. Una parentesi graffa viene utilizzata per indicare un sistema:

Diverse equazioni con una forma variabile insieme di equazioni, se il compito è trovare tutti questi valori di una variabile, ciascuno dei quali è la radice di almeno una di queste equazioni. Una parentesi quadra viene utilizzata per indicare una popolazione:

Equazioni contenenti una variabile sotto il segno del modulo.

Il valore assoluto di un numero UNè definito come segue:

Esempio: risolvere l'equazione

.

Soluzione: se

, Quello . Puoi scriverlo così:

Dall'Eq.

noi troviamo X= -9. Tuttavia, con questo valore della variabile, la disuguaglianza non regge, il che significa che il valore trovato non è la radice di questa equazione., Quello e questa equazione assumerà la forma. Puoi scriverlo così:

Dall'Eq.

noi troviamo . La disuguaglianza è vera, il che significa - la radice di questa equazione..

Equazioni con una variabile al denominatore.

Considera le equazioni della forma

. (1)

La soluzione di un'equazione di tipo (1) si basa sulla seguente affermazione: una frazione è uguale a 0 se e solo se il suo numeratore è uguale a 0 e il suo denominatore è diverso da zero.

In conformità con quanto sopra, la soluzione dell'equazione

si svolge in due fasi: prima è necessario risolvere l'equazione, e poi scoprire se, con i valori trovati della variabile, X denominatore a 0. Se q(x) ¹ 0 , quindi la radice trovata dell'equazioneè anche la radice dell'equazione (1); Seq(x) = 0, quindi la radice risultante dell'equazioneè anche la radice dell'equazione (1). Il sistema risultante è:

Dominio dell'equazione

f(x) = g(x) chiamare l'insieme di tutti quei valori di una variabile X, per cui l'espressionef(x) e l'espressione g(x)ha senso.

Se nel processo di trasformazione di un'equazione il suo dominio di definizione si è espanso, potrebbero apparire radici estranee. Pertanto, tutti i valori trovati della variabile devono essere controllati mediante sostituzione nell'equazione originale o utilizzando il dominio di definizione dell'equazione originale.

Equazioni razionali.

L'equazione

f(x) = g(x) chiamato razionale, Se f(x) e g(x)-espressioni razionali. Inoltre, se f(x) e g(x)- intere espressioni, quindi viene chiamata l'equazione Totale ;se almeno una delle espressionif(x), g(x)è frazionario, allora l'equazione razionalef(x) = g(x) chiamato frazionario .

Per risolvere un'equazione razionale, è necessario:

1. trova il denominatore comune di tutte le frazioni disponibili;
2. sostituisci questa equazione con una intera, moltiplicando entrambe le sue parti per un denominatore comune;
3. Risolvi l'intera equazione risultante;
4. Eliminare dalle radici ciò che fa svanire il comune denominatore.

Risolvere l'equazione

p(x) = 0 metodo di fattorizzazione. p(x) può essere fattorizzato: , quindi l'equazione prende forma . Se UN- radice dell'equazione, Quello , quindi almeno uno dei numeriè uguale a 0.

È vero anche il contrario: se X

= UN- la radice di almeno una delle equazioni , , , Quello UN- radice dell'equazione. Questo è

Risoluzione di equazioni

introducendo una nuova variabile.

Spieghiamo l'essenza del metodo con un esempio.

Esempio: risolvere l'equazione

.

Soluzione Mettiamo

, otteniamo l'equazione, dove troviamo . Il problema si riduce alla risoluzione di una serie di equazioni

Û

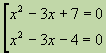
La prima equazione quadratica non ha radici reali, quindi il suo discriminante è negativo. Dal secondo troviamo

. Queste sono le radici dell'equazione data.

Un'equazione della forma è detta biquadratica

, Dove UN ¹ 0. L'equazione biquadratica si risolve introducendo una nuova variabile: mettendo , arriviamo all'equazione quadratica .

Equazioni irrazionali.

Irrazionale

è un'equazione in cui la variabile è contenuta sotto il segno della radice o sotto il segno dell'elevazione a potenza frazionaria. Un metodo per risolvere tali equazioni è quello di elevare entrambi i membri dell'equazione alla stessa potenza:

UN) trasformare l'equazione irrazionale data nella forma:

;

B) eleviamo entrambi i membri dell'equazione risultante a

N-esimo grado:

;

B) considerando ciò

, otteniamo l'equazione

f(x) = g(x);

)Risolviamo l'equazione ed eseguiamo un controllo, poiché elevare entrambi i lati dell'equazione a una potenza pari può portare alla comparsa di radici estranee. Questo controllo viene effettuato sostituendo i valori trovati della variabile nell'equazione originale.

Copyright © 2005-2013 Xenoid v2.0

L'utilizzo dei materiali del sito è possibile previo collegamento attivo.

Mantenere la tua privacy è importante per noi. Per questo motivo, abbiamo sviluppato un'Informativa sulla privacy che descrive come utilizziamo e archiviamo le tue informazioni. Si prega di rivedere le nostre pratiche sulla privacy e di farci sapere se avete domande.

Raccolta e utilizzo delle informazioni personali

Le informazioni personali si riferiscono ai dati che possono essere utilizzati per identificare o contattare una persona specifica.

Ti potrebbe essere chiesto di fornire le tue informazioni personali in qualsiasi momento quando ci contatti.

Di seguito sono riportati alcuni esempi dei tipi di informazioni personali che potremmo raccogliere e di come potremmo utilizzare tali informazioni.

Quali informazioni personali raccogliamo:

• Quando invii una richiesta sul sito, potremmo raccogliere varie informazioni, tra cui nome, numero di telefono, indirizzo email, ecc.

Come utilizziamo le tue informazioni personali:

• Le informazioni personali che raccogliamo ci consentono di contattarti con offerte uniche, promozioni e altri eventi ed eventi imminenti.
• Di tanto in tanto, potremmo utilizzare le tue informazioni personali per inviare avvisi e comunicazioni importanti.
• Potremmo anche utilizzare le informazioni personali per scopi interni, come condurre audit, analisi dei dati e varie ricerche al fine di migliorare i servizi che forniamo e fornirti consigli sui nostri servizi.
• Se partecipi a un'estrazione a premi, a un concorso o a una promozione simile, potremmo utilizzare le informazioni fornite per amministrare tali programmi.

Divulgazione di informazioni a terzi

Non divulghiamo le informazioni ricevute da te a terzi.

Eccezioni:

• Se necessario - in conformità alla legge, alla procedura giudiziaria, in procedimenti legali e/o sulla base di richieste pubbliche o richieste da parte delle autorità governative nel territorio della Federazione Russa - di divulgare i tuoi dati personali. Potremmo anche divulgare informazioni su di te se stabiliamo che tale divulgazione è necessaria o appropriata per motivi di sicurezza, applicazione della legge o altri scopi di importanza pubblica.
• In caso di riorganizzazione, fusione o vendita, potremmo trasferire le informazioni personali che raccogliamo alla terza parte successore applicabile.

Protezione delle informazioni personali

Prendiamo precauzioni, comprese quelle amministrative, tecniche e fisiche, per proteggere le tue informazioni personali da perdita, furto e uso improprio, nonché da accesso non autorizzato, divulgazione, alterazione e distruzione.

Rispettare la tua privacy a livello aziendale

Per garantire che le tue informazioni personali siano sicure, comunichiamo gli standard di privacy e sicurezza ai nostri dipendenti e applichiamo rigorosamente le pratiche sulla privacy.

Tipi di equazioni algebriche e metodi per risolverle

Per gli studenti interessati alla matematica, quando si risolvono equazioni algebriche di grado superiore, un metodo efficace per trovare rapidamente le radici, dividendo con resto per il binomio x -  o per ax + b, è lo schema di Horner.

Consideriamo lo schema di Horner.

Indichiamo il quoziente incompleto quando dividiamo P(x) per x –  attraverso

Q (x) = b 0 x n -1 + b 1 x n -2 + ... + b n -1, e il resto è b n.

Poiché P(x) = Q (x)(x–) + b n, allora vale l'uguaglianza

uno 0 x n + à 1 x n -1 + … + à n = (b 0 x n -1 + b 1 x n -2 + … + b n -1)(х– ) + b n

Apriamo le parentesi sul lato destro e confrontiamo i coefficienti per le stesse potenze di x a sinistra e a destra. Otteniamo che a 0 = b 0 e per 1  k  n valgono le relazioni a k ​​= b k -  b k -1. Ne consegue che b 0 = a 0 e b k = a k +  b k -1, 1  k  n.

Scriviamo il calcolo dei coefficienti del polinomio Q (x) e del resto b n sotto forma di tabella:

uno 0

un 1

un 2

UN n-1

UN N

b0 = a0

b1 = a1 + b0

b2 = a2 + b1

b n-1 = a n-1 +  b n-2

b n = a n +  b n-1

Esempio 1. Dividi il polinomio 2x 4 – 7x 3 – 3x 2 + 5x – 1 per x + 1.

Soluzione. Utilizziamo lo schema di Horner.

Dividendo 2x 4 – 7x 3 – 3x 2 + 5x – 1 per x + 1 otteniamo 2x 3 – 9x 2 + 6x – 1

Risposta: 2 x3 – 9x2 + 6x – 1

Esempio 2. Calcola P(3), dove P(x) = 4x 5 – 7x 4 + 5x 3 – 2x + 1

Soluzione. Utilizzando il teorema di Bezout e lo schema di Horner, otteniamo:

Risposta: P(3) = 535

Esercizio

Usando il diagramma di Horner, dividi il polinomio

4x 3 – x 5 + 132 – 8x 2 su x + 2;

2) Dividere il polinomio

2x 2 – 3x 3 – x + x 5 + 1 su x + 1;

3) Trovare il valore del polinomio P 5 (x) = 2x 5 – 4x 4 – x 2 + 1 per x = 7.

1.1. Trovare le radici razionali di equazioni a coefficienti interi

Il metodo per trovare le radici razionali di un'equazione algebrica a coefficienti interi è dato dal seguente teorema.

Teorema: Se un'equazione a coefficienti interi ha radici razionali, allora sono il quoziente di divisione del divisore del termine libero per il divisore del coefficiente principale.

Prova: a 0 x n + a 1 x n -1 + … + a n = 0

Sia x = p/ q è una radice razionale, q, p sono coprimi.

Sostituendo nell'equazione la frazione p/q e liberandoci del denominatore, otteniamo

a 0 r n + a 1 p n -1 q + … + a n -1 pq n -1 + a n q n = 0 (1)

Riscriviamo la (1) in due modi:

a n q n = р(– à 0 р n -1 – à 1 р n -2 q – … – à n -1 q n -1) (2)

a 0 r n = q (– а 1 р n -1 –… – а n -1 рq n -2 – а n q n -1) (3)

Dall'uguaglianza (2) segue che a n q n è divisibile per p, e poiché q n e p sono coprimi, allora a n è divisibile per p. Allo stesso modo, dall'uguaglianza (3) segue che a 0 è divisibile per q. Il teorema è stato dimostrato.

Esempio 1. Risolvi l'equazione 2x 3 – 7x 2 + 5x – 1 = 0.

Soluzione. L'equazione non ha radici intere; troviamo le radici razionali dell'equazione. Sia la frazione irriducibile p /q la radice dell'equazione, allora p si trova tra i divisori del termine libero, cioè tra i numeri  1, eq tra i divisori positivi del coefficiente principale: 1; 2.

Quelli. le radici razionali dell’equazione vanno ricercate tra i numeri  1,  1/2, denotano P 3 (x) = 2x 3 – 7x 2 + 5x – 1, P 3 (1)  0, P 3 (–1)  0,

P 3 (1/2) = 2/8 – 7/4 + 5/2 – 1 = 0, 1/2 è la radice dell'equazione.

2x 3 – 7x 2 + 5x – 1 = 2x 3 – x 2 – 6 x 2 + 3x + 2x – 1 = 0.

Noi abbiamo: x 2 (2x – 1) – 3x (2x – 1)+ (2x – 1) = 0; (2x – 1)(x 2 – 3x + 1) = 0.

Uguagliando il secondo fattore a zero e risolvendo l'equazione, otteniamo

Risposta:
,

Esercizi

Risolvi le equazioni:

6x3 – 25x2 + 3x + 4 = 0;

6x4 – 7x 3 – 6x 2 + 2x + 1 = 0;

3x 4 – 8x 3 – 2x 2 + 7x – 1 = 0;

1.2. Equazioni reciproche e metodi risolutivi

Definizione. Un'equazione a potenze intere rispetto ad un'incognita si dice reciproca se i suoi coefficienti, equidistanti dagli estremi del membro sinistro, sono uguali tra loro, cioè equazione della forma

UN x n + bx n -1 + cx n -2 + … + cx 2 + bx + a = 0

Equazione reciproca di grado dispari

UN x 2 n +1 + bx 2 n + cx 2 n -1 + … + cx 2 + bx + a = 0

ha sempre una radice x = – 1. Pertanto equivale a combinare l'equazione x + 1 = 0 e  x 2 n +  x 2 n -1 + … +  x +  = 0. L'ultima equazione è a equazione reciproca di grado pari. Pertanto, risolvere equazioni reciproche di qualsiasi grado si riduce a risolvere un'equazione reciproca di grado pari.

Come risolverlo? Sia data un'equazione reciproca di grado pari

UN x 2 n + bx 2 n -1 + … + dx n +1 + ex n + dx n -1 + … + bx + a = 0

Nota che x = 0 non è la radice dell'equazione. Quindi dividiamo l'equazione per x n, otteniamo

UN x n + bx n -1 + … + dx + e + dx -1 + … + bx 1- n + аx -n = 0

Raggruppiamo i termini del lato sinistro a coppie

UN( x n + x - n ) + b (x n -1 + x -(n -1) + … + d(x + x -1 ) + e = 0

Facciamo la sostituzione x + x -1 = y. Dopo aver sostituito le espressioni x 2 + x -2 = y 2 – 2;

x3 + x -3 = y3 – 3y; x 4 + x -4 = y 4 – 4y + 2 nell'equazione per cui otteniamo l'equazione AÀу n + By n -1 +Cy n -2 + … + Ey + D = 0.

Per risolvere questa equazione, è necessario risolvere diverse equazioni quadratiche della forma x + x -1 = y k, dove k = 1, 2, ... n. Pertanto, otteniamo le radici dell'equazione originale.

Esempio 1. Risolvi l'equazione x 7 + x 6 – 5x 5 – 13x 4 – 13x 3 – 5x 2 + 2x + 1 = 0.

Soluzione. x = – 1 è la radice dell'equazione. Applichiamo lo schema di Horner.

La nostra equazione assumerà la forma:

(x + 1)(x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1) = 0

1) x + 1 = 0, x = -1;

2) x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1 = 0 | :x3  0; x 3 + x 2 – 6x – 7 – 6/x + 1/x 2 + 1/x 3 =0.

Raggruppando, otteniamo: .

Introduciamo una sostituzione:
;
;
.

Otteniamo relativamente A equazione: y 3 – 3y + y 2 – 2 – 6y – 7 = 0;

y3 + y2 – 9y – 9 = 0; y2 (y+1) – 9 (y+1) = 0; (y + 1)(y 2 – 9); y 1 = -1, y 2,3 =  3.

Risoluzione di equazioni
,
,
,

otteniamo le radici:
,
,
,

Risposta: x 1 = -1,
,

Esercizi

Risolvere equazioni.

2x 5 + 5x 4 – 13x 3 – 13x 2 + 5x + 2 = 0;

2x 4 + 3x 3 – 16x 2 + 3x + 2 = 0;

15x 5 + 34x 4 + 15x 3 – 15x 2 – 34x – 15 = 0.

1.3. Metodo di sostituzione delle variabili per la risoluzione di equazioni

Il metodo di sostituzione delle variabili è il metodo più comune. L’arte di apportare un cambiamento variabile è vedere quale cambiamento ha più senso e porterà al successo più rapidamente.

Se data l'equazione

F(f(x)) = 0, (1)

quindi sostituendo l'incognita y = f (x) si riduce prima all'equazione

F(y) = 0, (2)

e quindi dopo aver trovato tutte le soluzioni dell'equazione (2) y 1, y 2, ..., y n, ... si riduce a risolvere l'insieme di equazioni f (x) = y 1, f (x) = y 2 ,..., f(x) = y 2,...

I modi principali per implementare il metodo di sostituzione delle variabili sono:

utilizzando la proprietà di base di una frazione;

evidenziando il quadrato del binomio;

transizione a un sistema di equazioni;

parentesi di apertura a coppie;

aprire parentesi a coppie e dividere entrambi i lati dell'equazione;

diminuendo il grado dell'equazione;

doppia sostituzione.

1.3.1. Ridurre la potenza di un'equazione

Risolvi l'equazione (x 2 + x + 2)(x 2 + x + 3) = 6 (3)

Soluzione. Indichiamo x 2 + x + 2 = y, quindi prendiamo y (y + 1) = 6, risolvendo quest'ultimo, otteniamo y 1 = 2, y 2 = -3. Questa equazione (3) è equivalente all'insieme di equazioni x 2 + x + 2 = 2

x2 + x+2 = -3

Risolvendo il primo, otteniamo x 1 = 0,x2 = -1. Risolvendo il secondo, otteniamo
,

Risposta: x1 = 0, x2 = -1,

1.3.2. Equazione di quarto grado della forma (x + a)(x +B )(X + C )(X + D ) = M , dove a + b = c + d, oppure a + c = b + d, oppure a + d = b + c.

Esempio. Risolvi l'equazione (x - 1)(x - 7)(x -4)(x + 2) = 40

Soluzione. – 1- 4 = - 7 + 2, - 5 = - 5, moltiplicando queste coppie di parentesi, otteniamo l'equazione (x 2 - 5x - 14)(x 2 - 5x + 4) = 40

Introduciamo la sostituzione: x 2 - 5x – 14 = y, otteniamo l'equazione y(y + 18) = 40, y 2 + 18y = 40, y 2 + 18y – 40 = 0. y 1 = -20, y 2 = 2. Ritornando alla variabile originale, risolviamo una serie di equazioni:

X2 - 5x – 14 = - 20x1 = 2; x2 = 3

x2 - 5x – 14 = 2x3,4 =

Risposta: x1 = 2; x2 = 3x3,4 =

1.3.3. Un'equazione della forma (x + a)(x + b)(x + c)(x + d) = Ex 2,

Dove ab = cd, oppure ac =bd, oppure ad = bc. Apri le parentesi a coppie e dividi entrambe le parti per x 2  0.

Esempio. (x - 1)(x - 2)(x - 8)(x - 4) = 4x 2

Soluzione. Il prodotto dei numeri nella prima e terza e nella seconda e quarta parentesi sono uguali, cioè – 8 (- 1) = (- 2)(- 4). Moltiplichiamo le coppie di parentesi indicate e scriviamo l'equazione (x 2 - 9x + 8)(x 2 - 6x + 8) = 4x 2.

Poiché x = 0 non è la radice dell'equazione, dividiamo entrambi i membri dell'equazione per x 2  0, otteniamo:
, sostituzione:
, l'equazione originale assumerà la forma:T(T+3) =4, T 2 + 3 T=4, T 2 + 3 T – 4=0, T 1 =1, T 2 = - 4.

Torniamo alla variabile originale:

x2 - 10x + 8 = 0

x2 - 5x + 8 = 0

Risolviamo la prima equazione, otteniamo x 1,2 = 5 

La seconda equazione non ha radici.

Risposta: x 1,2 = 5 

1.3.4. Equazione del quarto tipo (ax 2 + b 1 x + c)(a x 2 + b 2 x + c) = A x 2

Equazione (asse 2 + B 1x+ C)(UN x2+ B 2 X + C) = UN x 2, dove c  0, A  2
, che dopo aver sostituito l'ignoto
può essere riscritto come un quadrato e può essere facilmente risolto.

Esempio. (x2 + x+ 2)(x2 + 2x + 2) = 2x2

Soluzione. È facile vedere che x = 0 non è una radice di questa equazione dividendo questa equazione per x 2 , otteniamo l'equazione

sostituzione
, otteniamo l'equazione (y+1)(y+2) = 2, risolvendola abbiamo le radici y 1 = 0; alle 2 = - 3, quindi l'equazione originale è equivalente all'insieme di equazioni

risolvendo si ottiene x 1 = -1; x2 = -2.

Risposta: x1 = -1; x2 = -2

1.3.5. Equazione della forma: a (cx 2 + p 1 x + q) 2 + b (cx 2 + p 2 x + q) 2 = Ax 2

L'equazione UN(cx 2 + P 1 X + Q) 2 + B(cx 2 + P 2 X + Q) 2 = Ascia 2 dove UN, B, C, Q, UN sono tali Q 0, UN 0, C 0, UN 0, B 0 non ha radice x = 0, quindi divido l'equazione per x 2 , otteniamo un'equazione equivalente
, che dopo la sostituzione
può essere riscritta come un'equazione quadratica facilmente risolvibile. + 1)( x2 – 14x + 15 = 0

X 2 – 7 X + 15 = 0

Risposta:

In alcuni problemi di fisica non è possibile stabilire una connessione diretta tra le quantità che descrivono il processo. Ma è possibile ottenere un'uguaglianza contenente le derivate delle funzioni studiate. Ecco come nascono le equazioni differenziali e la necessità di risolverle per trovare una funzione sconosciuta.

Questo articolo è destinato a coloro che si trovano ad affrontare il problema di risolvere un'equazione differenziale in cui la funzione sconosciuta è una funzione di una variabile. La teoria è strutturata in modo tale che con una conoscenza pari a zero delle equazioni differenziali puoi far fronte al tuo compito.

Ad ogni tipo di equazione differenziale è associato un metodo di soluzione con spiegazioni dettagliate e soluzioni ad esempi e problemi tipici. Tutto quello che devi fare è determinare il tipo di equazione differenziale del tuo problema, trovare un esempio analizzato simile ed eseguire azioni simili.

Per risolvere con successo le equazioni differenziali, avrai anche bisogno della capacità di trovare insiemi di antiderivative (integrali indefiniti) di varie funzioni. Se necessario, si consiglia di fare riferimento alla sezione.

Considereremo dapprima le tipologie di equazioni differenziali ordinarie del primo ordine risolvibili rispetto alla derivata, poi passeremo alle ODE del secondo ordine, quindi ci soffermeremo sulle equazioni di ordine superiore e termineremo con i sistemi di equazioni differenziali.

Ricordiamo che se y è una funzione dell'argomento x.

Equazioni differenziali del primo ordine.

Le più semplici equazioni differenziali del primo ordine della forma.

Scriviamo alcuni esempi di tale controllo remoto .

Equazioni differenziali può essere risolto rispetto alla derivata dividendo entrambi i membri dell'uguaglianza per f(x) . In questo caso arriviamo a un'equazione che sarà equivalente a quella originale per f(x) ≠ 0. Esempi di tali ODE sono .

Se ci sono valori dell'argomento x in cui le funzioni f(x) e g(x) svaniscono contemporaneamente, compaiono soluzioni aggiuntive. Ulteriori soluzioni all'equazione dato x sono le funzioni definite per questi valori di argomento. Esempi di tali equazioni differenziali includono:

Equazioni differenziali del secondo ordine.

Equazioni differenziali lineari omogenee del secondo ordine a coefficienti costanti.

LDE con coefficienti costanti è un tipo molto comune di equazione differenziale. La loro soluzione non è particolarmente difficile. Per prima cosa si trovano le radici dell'equazione caratteristica . Per p e q diversi sono possibili tre casi: le radici dell'equazione caratteristica possono essere reali e diverse, reali e coincidenti o coniugati complessi. A seconda dei valori delle radici dell'equazione caratteristica, la soluzione generale dell'equazione differenziale viene scritta come , O , o rispettivamente.

Ad esempio, consideriamo un'equazione differenziale lineare omogenea del secondo ordine con coefficienti costanti. Le radici della sua equazione caratteristica sono k 1 = -3 e k 2 = 0. Le radici sono reali e diverse, quindi la soluzione generale del LODE a coefficienti costanti ha la forma


Equazioni differenziali lineari disomogenee del secondo ordine a coefficienti costanti.

La soluzione generale di un LDDE del secondo ordine a coefficienti costanti y viene cercata sotto forma di somma della soluzione generale del corrispondente LDDE e una soluzione particolare all'equazione disomogenea originale, cioè . Il paragrafo precedente è dedicato alla ricerca di una soluzione generale per un'equazione differenziale omogenea a coefficienti costanti. E una soluzione particolare è determinata o dal metodo dei coefficienti indefiniti per una certa forma della funzione f(x) sul lato destro dell'equazione originale, o dal metodo della variazione delle costanti arbitrarie.

Come esempi di LDDE del secondo ordine con coefficienti costanti, diamo


Per comprendere la teoria e conoscere soluzioni dettagliate di esempi, ti offriamo nella pagina equazioni differenziali lineari disomogenee del secondo ordine con coefficienti costanti.

Equazioni differenziali omogenee lineari (LODE) ed equazioni differenziali lineari disomogenee (LNDE) del secondo ordine.

Un caso particolare di equazioni differenziali di questo tipo sono LODE e LDDE a coefficienti costanti.

La soluzione generale del LODE su un certo segmento è rappresentata da una combinazione lineare di due soluzioni parziali linearmente indipendenti y 1 e y 2 di questa equazione, cioè, .

La difficoltà principale sta proprio nel trovare soluzioni parziali linearmente indipendenti di un'equazione differenziale di questo tipo. Tipicamente, soluzioni particolari vengono selezionate dai seguenti sistemi di funzioni linearmente indipendenti:


Tuttavia, le soluzioni particolari non vengono sempre presentate in questa forma.

Un esempio di LOD è .

La soluzione generale dell'LDDE si cerca nella forma , dove è la soluzione generale del corrispondente LDDE, ed è la soluzione particolare dell'equazione differenziale originaria. Abbiamo appena parlato di trovarlo, ma può essere determinato utilizzando il metodo della variazione delle costanti arbitrarie.

Si può fornire un esempio di LNDU .

Equazioni differenziali di ordine superiore.

Equazioni differenziali che consentono una riduzione dell'ordine.

Ordine delle equazioni differenziali , che non contiene la funzione desiderata e le sue derivate fino all'ordine k-1, può essere ridotto a n-k sostituendo .

In questo caso, l'equazione differenziale originale verrà ridotta a . Dopo aver trovato la sua soluzione p(x), resta da ritornare alla sostituzione e determinare la funzione sconosciuta y.

Ad esempio, l'equazione differenziale dopo la sostituzione diventerà un'equazione a variabili separabili e il suo ordine verrà ridotto dalla terza alla prima.