ಕೋನಗಳ ಮೊತ್ತ ಎಷ್ಟು? ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತದ ಪ್ರಮೇಯ. ಕೋನದ ಗಾತ್ರದಿಂದ ವಿಧಗಳು

ತ್ರಿಕೋನ ಕೋನಗಳ ಮೊತ್ತ- ಮುಖ್ಯ, ಆದರೆ ಸಾಕು ಸರಳ ಥೀಮ್, ಇದು 7 ನೇ ತರಗತಿಯ ರೇಖಾಗಣಿತದಲ್ಲಿ ಕಲಿಸಲಾಗುತ್ತದೆ. ವಿಷಯವು ಒಂದು ಪ್ರಮೇಯ, ಒಂದು ಸಣ್ಣ ಪುರಾವೆ ಮತ್ತು ಹಲವಾರು ತಾರ್ಕಿಕ ಪರಿಣಾಮಗಳನ್ನು ಒಳಗೊಂಡಿದೆ. ಈ ವಿಷಯದ ಜ್ಞಾನವು ಪರಿಹರಿಸುವಲ್ಲಿ ಸಹಾಯ ಮಾಡುತ್ತದೆ ಜ್ಯಾಮಿತೀಯ ಸಮಸ್ಯೆಗಳುವಿಷಯದ ನಂತರದ ಅಧ್ಯಯನದ ಸಮಯದಲ್ಲಿ.

ಪ್ರಮೇಯ - ಅನಿಯಂತ್ರಿತ ತ್ರಿಕೋನದ ಕೋನಗಳನ್ನು ಒಟ್ಟಿಗೆ ಸೇರಿಸಲಾಗುತ್ತದೆ?

ನೀವು ಯಾವುದೇ ತ್ರಿಕೋನವನ್ನು ತೆಗೆದುಕೊಂಡರೆ, ಅದರ ಪ್ರಕಾರವನ್ನು ಲೆಕ್ಕಿಸದೆ, ಎಲ್ಲಾ ಕೋನಗಳ ಮೊತ್ತವು ಏಕರೂಪವಾಗಿ 180 ಡಿಗ್ರಿಗಳಾಗಿರುತ್ತದೆ ಎಂದು ಪ್ರಮೇಯ ಹೇಳುತ್ತದೆ. ಇದು ಈ ಕೆಳಗಿನಂತೆ ಸಾಬೀತಾಗಿದೆ:

• ಉದಾಹರಣೆಗೆ, ABC ತ್ರಿಕೋನವನ್ನು ತೆಗೆದುಕೊಳ್ಳಿ, ತುದಿಯಲ್ಲಿರುವ B ಬಿಂದುವಿನ ಮೂಲಕ ಸರಳ ರೇಖೆಯನ್ನು ಎಳೆಯಿರಿ ಮತ್ತು ಅದನ್ನು "a" ಎಂದು ಗೊತ್ತುಪಡಿಸಿ, "a" ನೇರ ರೇಖೆಯು AC ಬದಿಗೆ ಕಟ್ಟುನಿಟ್ಟಾಗಿ ಸಮಾನಾಂತರವಾಗಿರುತ್ತದೆ;
• ನೇರ ರೇಖೆ "a" ಮತ್ತು AB ಮತ್ತು BC ಬದಿಗಳ ನಡುವೆ, ಕೋನಗಳನ್ನು ಗೊತ್ತುಪಡಿಸಲಾಗುತ್ತದೆ, ಅವುಗಳನ್ನು 1 ಮತ್ತು 2 ಸಂಖ್ಯೆಗಳೊಂದಿಗೆ ಗುರುತಿಸಲಾಗುತ್ತದೆ;
• ಕೋನ 1 ಅನ್ನು ಕೋನ A ಗೆ ಸಮಾನವೆಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ಕೋನ 2 ಅನ್ನು ಕೋನ C ಗೆ ಸಮನಾಗಿರುತ್ತದೆ, ಏಕೆಂದರೆ ಈ ಕೋನಗಳು ಅಡ್ಡಲಾಗಿ ಇರುತ್ತವೆ ಎಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ;
• ಹೀಗಾಗಿ, 1, 2 ಮತ್ತು 3 ಕೋನಗಳ ನಡುವಿನ ಮೊತ್ತವನ್ನು (ಕೋನ B ಯ ಸ್ಥಳದಲ್ಲಿ ಗೊತ್ತುಪಡಿಸಲಾಗಿದೆ) B ಶೃಂಗದೊಂದಿಗೆ ಬಿಚ್ಚಿದ ಕೋನಕ್ಕೆ ಸಮಾನವಾಗಿ ಗುರುತಿಸಲಾಗಿದೆ - ಮತ್ತು 180 ಡಿಗ್ರಿ.

ಸಂಖ್ಯೆಗಳಿಂದ ಸೂಚಿಸಲಾದ ಕೋನಗಳ ಮೊತ್ತವು 180 ಡಿಗ್ರಿಗಳಾಗಿದ್ದರೆ, A, B ಮತ್ತು C ಕೋನಗಳ ಮೊತ್ತವನ್ನು 180 ಡಿಗ್ರಿಗಳಿಗೆ ಸಮಾನವೆಂದು ಗುರುತಿಸಲಾಗುತ್ತದೆ. ಈ ನಿಯಮವು ಯಾವುದೇ ತ್ರಿಕೋನಕ್ಕೆ ನಿಜವಾಗಿದೆ.

ಜ್ಯಾಮಿತೀಯ ಪ್ರಮೇಯದಿಂದ ಏನು ಅನುಸರಿಸುತ್ತದೆ

ಮೇಲಿನ ಪ್ರಮೇಯದಿಂದ ಹಲವಾರು ಅನುಬಂಧಗಳನ್ನು ಎತ್ತಿ ತೋರಿಸುವುದು ವಾಡಿಕೆ.

• ಸಮಸ್ಯೆಯು ಲಂಬ ಕೋನದೊಂದಿಗೆ ತ್ರಿಕೋನವನ್ನು ಪರಿಗಣಿಸಿದರೆ, ಅದರ ಒಂದು ಕೋನವು ಪೂರ್ವನಿಯೋಜಿತವಾಗಿ 90 ಡಿಗ್ರಿಗಳಿಗೆ ಸಮನಾಗಿರುತ್ತದೆ ಮತ್ತು ತೀವ್ರ ಕೋನಗಳ ಮೊತ್ತವು 90 ಡಿಗ್ರಿಗಳಾಗಿರುತ್ತದೆ.
• ನಾವು ಬಲ ಸಮದ್ವಿಬಾಹು ತ್ರಿಕೋನದ ಬಗ್ಗೆ ಮಾತನಾಡುತ್ತಿದ್ದರೆ, ಅದರ ತೀವ್ರ ಕೋನಗಳು, 90 ಡಿಗ್ರಿಗಳವರೆಗೆ, ಪ್ರತ್ಯೇಕವಾಗಿ 45 ಡಿಗ್ರಿಗಳಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.
• ಒಂದು ಸಮಬಾಹು ತ್ರಿಕೋನವು ಕ್ರಮವಾಗಿ ಮೂರು ಸಮಾನ ಕೋನಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಅವುಗಳಲ್ಲಿ ಪ್ರತಿಯೊಂದೂ 60 ಡಿಗ್ರಿಗಳಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ಒಟ್ಟಾರೆಯಾಗಿ ಅವು 180 ಡಿಗ್ರಿಗಳಾಗಿರುತ್ತದೆ.
• ಯಾವುದೇ ತ್ರಿಕೋನದ ಬಾಹ್ಯ ಕೋನವು ಅದರ ಪಕ್ಕದಲ್ಲಿಲ್ಲದ ಎರಡು ಆಂತರಿಕ ಕೋನಗಳ ನಡುವಿನ ಮೊತ್ತಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ.

ಕೆಳಗಿನ ನಿಯಮವನ್ನು ಪಡೆಯಬಹುದು: ಯಾವುದೇ ತ್ರಿಕೋನವು ಕನಿಷ್ಠ ಎರಡು ತೀವ್ರ ಕೋನಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಕೆಲವು ಸಂದರ್ಭಗಳಲ್ಲಿ, ಒಂದು ತ್ರಿಕೋನವು ಮೂರು ತೀವ್ರ ಕೋನಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಮತ್ತು ಕೇವಲ ಎರಡು ಇದ್ದರೆ, ಮೂರನೇ ಕೋನವು ಚೂಪಾದ ಅಥವಾ ಬಲವಾಗಿರುತ್ತದೆ.

ಪ್ರಮೇಯ. ತ್ರಿಕೋನದ ಆಂತರಿಕ ಕೋನಗಳ ಮೊತ್ತವು ಎರಡು ಲಂಬ ಕೋನಗಳಿಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ಕೆಲವು ತ್ರಿಕೋನ ಎಬಿಸಿಯನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ (ಚಿತ್ರ 208). ನಾವು ಅದರ ಆಂತರಿಕ ಕೋನಗಳನ್ನು 1, 2 ಮತ್ತು 3 ಸಂಖ್ಯೆಗಳಿಂದ ಸೂಚಿಸೋಣ. ನಾವು ಅದನ್ನು ಸಾಬೀತುಪಡಿಸೋಣ

∠1 + ∠2 + ∠3 = 180°.

ನಾವು ತ್ರಿಕೋನದ ಕೆಲವು ಶೃಂಗದ ಮೂಲಕ ಸೆಳೆಯೋಣ, ಉದಾಹರಣೆಗೆ B, AC ಗೆ ಸಮಾನಾಂತರವಾಗಿರುವ ಸರಳ ರೇಖೆ MN.

B ಶೃಂಗದಲ್ಲಿ ನಾವು ಮೂರು ಕೋನಗಳನ್ನು ಪಡೆದುಕೊಂಡಿದ್ದೇವೆ: ∠4, ∠2 ಮತ್ತು ∠5. ಅವುಗಳ ಮೊತ್ತವು ನೇರ ಕೋನವಾಗಿದೆ, ಆದ್ದರಿಂದ ಇದು 180 ° ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ:

∠4 + ∠2 + ∠5 = 180°.

ಆದರೆ ∠4 = ∠1 ಸಮಾನಾಂತರ ರೇಖೆಗಳು MN ಮತ್ತು AC ಮತ್ತು ಸೆಕೆಂಟ್ AB ಹೊಂದಿರುವ ಆಂತರಿಕ ಅಡ್ಡ ಕೋನಗಳಾಗಿವೆ.

∠5 = ∠3 - ಇವುಗಳು ಸಮಾನಾಂತರ ರೇಖೆಗಳು MN ಮತ್ತು AC ಮತ್ತು ಸೆಕೆಂಟ್ BC ಯೊಂದಿಗೆ ಆಂತರಿಕ ಅಡ್ಡ ಕೋನಗಳಾಗಿವೆ.

ಇದರರ್ಥ ∠4 ಮತ್ತು ∠5 ಅನ್ನು ಅವುಗಳ ಸಮಾನ ∠1 ಮತ್ತು ∠3 ಗಳಿಂದ ಬದಲಾಯಿಸಬಹುದು.

ಆದ್ದರಿಂದ, ∠1 + ∠2 + ∠3 = 180°. ಪ್ರಮೇಯವು ಸಾಬೀತಾಗಿದೆ.

2. ತ್ರಿಕೋನದ ಬಾಹ್ಯ ಕೋನದ ಆಸ್ತಿ.

ವಾಸ್ತವವಾಗಿ, ABC ತ್ರಿಕೋನದಲ್ಲಿ (Fig. 209) ∠1 + ∠2 = 180 ° - ∠3, ಆದರೆ ∠ВСD, ಈ ತ್ರಿಕೋನದ ಬಾಹ್ಯ ಕೋನವು ∠1 ಮತ್ತು ∠2 ಗೆ ಹೊಂದಿಕೆಯಾಗುವುದಿಲ್ಲ, ಇದು 180 ° ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. - ∠3 .

ಹೀಗೆ:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

ಆದ್ದರಿಂದ, ∠1 + ∠2= ∠BCD.

ತ್ರಿಕೋನದ ಬಾಹ್ಯ ಕೋನದಿಂದ ಪಡೆದ ಆಸ್ತಿಯು ತ್ರಿಕೋನದ ಬಾಹ್ಯ ಕೋನದಲ್ಲಿ ಹಿಂದೆ ಸಾಬೀತಾಗಿರುವ ಪ್ರಮೇಯದ ವಿಷಯವನ್ನು ಸ್ಪಷ್ಟಪಡಿಸುತ್ತದೆ, ಇದು ತ್ರಿಕೋನದ ಬಾಹ್ಯ ಕೋನವು ಅದರ ಪಕ್ಕದಲ್ಲಿಲ್ಲದ ತ್ರಿಕೋನದ ಪ್ರತಿಯೊಂದು ಆಂತರಿಕ ಕೋನಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ ಎಂದು ಮಾತ್ರ ಹೇಳುತ್ತದೆ; ಬಾಹ್ಯ ಕೋನವು ಅದರ ಪಕ್ಕದಲ್ಲಿಲ್ಲದ ಎರಡೂ ಆಂತರಿಕ ಕೋನಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿದೆ ಎಂದು ಈಗ ಸ್ಥಾಪಿಸಲಾಗಿದೆ.

3. 30 ° ಕೋನದೊಂದಿಗೆ ಬಲ ತ್ರಿಕೋನದ ಆಸ್ತಿ.

ಬಲ ತ್ರಿಕೋನ ACB ಯಲ್ಲಿ ಕೋನ B 30 ° ಗೆ ಸಮನಾಗಿರುತ್ತದೆ (ಚಿತ್ರ 210). ನಂತರ ಅದರ ಇತರ ತೀವ್ರ ಕೋನವು 60 ° ಗೆ ಸಮನಾಗಿರುತ್ತದೆ.

ಲೆಗ್ ಎಸಿ ಅರ್ಧ ಹೈಪೊಟೆನ್ಯೂಸ್ ಎಬಿಗೆ ಸಮಾನವಾಗಿದೆ ಎಂದು ನಾವು ಸಾಬೀತುಪಡಿಸೋಣ. ಲೆಗ್ AC ಅನ್ನು ಲಂಬ ಕೋನ C ಯ ಶೃಂಗದ ಆಚೆಗೆ ವಿಸ್ತರಿಸೋಣ ಮತ್ತು AC ಯ ಭಾಗಕ್ಕೆ ಸಮಾನವಾದ ಸೆಗ್ಮೆಂಟ್ CM ಅನ್ನು ಪಕ್ಕಕ್ಕೆ ಇಡೋಣ. ಪಾಯಿಂಟ್ B ಗೆ ಪಾಯಿಂಟ್ ಅನ್ನು ಸಂಪರ್ಕಿಸೋಣ. ಪರಿಣಾಮವಾಗಿ ತ್ರಿಕೋನ ВСМ ತ್ರಿಕೋನ ACB ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ. ABM ತ್ರಿಕೋನದ ಪ್ರತಿಯೊಂದು ಕೋನವು 60 ° ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಎಂದು ನಾವು ನೋಡುತ್ತೇವೆ, ಆದ್ದರಿಂದ ಈ ತ್ರಿಕೋನವು ಸಮಬಾಹು ತ್ರಿಕೋನವಾಗಿದೆ.

ಲೆಗ್ AC ಅರ್ಧ AM ಗೆ ಸಮ, ಮತ್ತು AM AB ಗೆ ಸಮಾನವಾಗಿರುವುದರಿಂದ, ಲೆಗ್ AC ಅರ್ಧ ಹೈಪೊಟೆನ್ಯೂಸ್ AB ಗೆ ಸಮನಾಗಿರುತ್ತದೆ.

ತ್ರಿಕೋನದ ಆಂತರಿಕ ಕೋನಗಳ ಮೊತ್ತವು 180 0 ಆಗಿದೆ. ಇದು ಯೂಕ್ಲಿಡ್‌ನ ರೇಖಾಗಣಿತದ ಮೂಲಭೂತ ಮೂಲತತ್ವಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ. ಇದು ಶಾಲಾ ಮಕ್ಕಳು ಅಧ್ಯಯನ ಮಾಡುವ ರೇಖಾಗಣಿತವಾಗಿದೆ. ಜ್ಯಾಮಿತಿಯನ್ನು ನೈಜ ಪ್ರಪಂಚದ ಪ್ರಾದೇಶಿಕ ರೂಪಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡುವ ವಿಜ್ಞಾನ ಎಂದು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ.

ಜ್ಯಾಮಿತಿಯನ್ನು ಅಭಿವೃದ್ಧಿಪಡಿಸಲು ಪ್ರಾಚೀನ ಗ್ರೀಕರು ಏನು ಪ್ರೇರೇಪಿಸಿದರು? ಜಾಗ, ಹುಲ್ಲುಗಾವಲುಗಳನ್ನು ಅಳೆಯುವ ಅವಶ್ಯಕತೆ - ಭೂಮಿಯ ಮೇಲ್ಮೈಯ ಪ್ರದೇಶಗಳು. ಅದೇ ಸಮಯದಲ್ಲಿ, ಪ್ರಾಚೀನ ಗ್ರೀಕರು ಭೂಮಿಯ ಮೇಲ್ಮೈ ಸಮತಲ ಮತ್ತು ಸಮತಟ್ಟಾಗಿದೆ ಎಂದು ಒಪ್ಪಿಕೊಂಡರು. ಈ ಊಹೆಯನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಂಡು, 180 0 ರ ತ್ರಿಕೋನದ ಆಂತರಿಕ ಕೋನಗಳ ಮೊತ್ತವನ್ನು ಒಳಗೊಂಡಂತೆ ಯೂಕ್ಲಿಡ್ನ ಮೂಲತತ್ವಗಳನ್ನು ರಚಿಸಲಾಗಿದೆ.

ಒಂದು ಮೂಲತತ್ವವು ಪುರಾವೆ ಅಗತ್ಯವಿಲ್ಲದ ಪ್ರತಿಪಾದನೆಯಾಗಿದೆ. ಇದನ್ನು ಹೇಗೆ ಅರ್ಥಮಾಡಿಕೊಳ್ಳಬೇಕು? ವ್ಯಕ್ತಿಗೆ ಸೂಕ್ತವಾದ ಒಂದು ಆಶಯವನ್ನು ವ್ಯಕ್ತಪಡಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ನಂತರ ಅದನ್ನು ದೃಷ್ಟಾಂತಗಳ ಮೂಲಕ ದೃಢೀಕರಿಸಲಾಗುತ್ತದೆ. ಆದರೆ ಸಾಬೀತಾಗದ ಎಲ್ಲವೂ ಕಾಲ್ಪನಿಕ, ವಾಸ್ತವದಲ್ಲಿ ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲ.

ಭೂಮಿಯ ಮೇಲ್ಮೈಯನ್ನು ಸಮತಲವಾಗಿ ತೆಗೆದುಕೊಂಡು, ಪ್ರಾಚೀನ ಗ್ರೀಕರು ಭೂಮಿಯ ಆಕಾರವನ್ನು ಸ್ವಯಂಚಾಲಿತವಾಗಿ ಸಮತಟ್ಟಾಗಿ ಸ್ವೀಕರಿಸಿದರು, ಆದರೆ ಅದು ವಿಭಿನ್ನವಾಗಿದೆ - ಗೋಳಾಕಾರದ. ಪ್ರಕೃತಿಯಲ್ಲಿ ಯಾವುದೇ ಸಮತಲ ಸಮತಲಗಳು ಅಥವಾ ನೇರ ರೇಖೆಗಳಿಲ್ಲ, ಏಕೆಂದರೆ ಗುರುತ್ವಾಕರ್ಷಣೆಯು ಜಾಗವನ್ನು ಬಾಗುತ್ತದೆ. ನೇರ ರೇಖೆಗಳು ಮತ್ತು ಸಮತಲ ಸಮತಲಗಳು ಮಾನವ ಮೆದುಳಿನಲ್ಲಿ ಮಾತ್ರ ಕಂಡುಬರುತ್ತವೆ.

ಆದ್ದರಿಂದ, ಕಾಲ್ಪನಿಕ ಪ್ರಪಂಚದ ಪ್ರಾದೇಶಿಕ ರೂಪಗಳನ್ನು ವಿವರಿಸುವ ಯೂಕ್ಲಿಡ್‌ನ ರೇಖಾಗಣಿತವು ಒಂದು ಸಿಮ್ಯುಲಾಕ್ರಮ್ ಆಗಿದೆ - ಇದು ಮೂಲವನ್ನು ಹೊಂದಿರದ ನಕಲು.

ಯೂಕ್ಲಿಡ್‌ನ ಮೂಲತತ್ವಗಳಲ್ಲಿ ಒಂದು ತ್ರಿಕೋನದ ಆಂತರಿಕ ಕೋನಗಳ ಮೊತ್ತವು 180 0 ಎಂದು ಹೇಳುತ್ತದೆ. ವಾಸ್ತವವಾಗಿ, ನಿಜವಾದ ಬಾಗಿದ ಜಾಗದಲ್ಲಿ ಅಥವಾ ಭೂಮಿಯ ಗೋಳಾಕಾರದ ಮೇಲ್ಮೈಯಲ್ಲಿ, ತ್ರಿಕೋನದ ಆಂತರಿಕ ಕೋನಗಳ ಮೊತ್ತವು ಯಾವಾಗಲೂ 180 0 ಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ.

ಹೀಗೆ ಯೋಚಿಸೋಣ. ಭೂಗೋಳದ ಯಾವುದೇ ಮೆರಿಡಿಯನ್ ಸಮಭಾಜಕದೊಂದಿಗೆ 90 0 ಕೋನದಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ. ತ್ರಿಕೋನವನ್ನು ಪಡೆಯಲು, ನೀವು ಮೆರಿಡಿಯನ್‌ನಿಂದ ಮತ್ತೊಂದು ಮೆರಿಡಿಯನ್ ಅನ್ನು ಚಲಿಸಬೇಕಾಗುತ್ತದೆ. ಮೆರಿಡಿಯನ್ಸ್ ಮತ್ತು ಸಮಭಾಜಕದ ಬದಿಯ ನಡುವಿನ ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತವು 180 0 ಆಗಿರುತ್ತದೆ. ಆದರೆ ಧ್ರುವದಲ್ಲಿ ಇನ್ನೂ ಒಂದು ಕೋನ ಇರುತ್ತದೆ. ಪರಿಣಾಮವಾಗಿ, ಎಲ್ಲಾ ಕೋನಗಳ ಮೊತ್ತವು 180 0 ಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ.

ಧ್ರುವದಲ್ಲಿ ಬದಿಗಳು 90 0 ಕೋನದಲ್ಲಿ ಛೇದಿಸಿದರೆ, ಅಂತಹ ತ್ರಿಕೋನದ ಆಂತರಿಕ ಕೋನಗಳ ಮೊತ್ತವು 270 0 ಆಗಿರುತ್ತದೆ. ಈ ತ್ರಿಕೋನದಲ್ಲಿ ಸಮಭಾಜಕವನ್ನು ಲಂಬ ಕೋನಗಳಲ್ಲಿ ಛೇದಿಸುವ ಎರಡು ಮೆರಿಡಿಯನ್‌ಗಳು ಪರಸ್ಪರ ಸಮಾನಾಂತರವಾಗಿರುತ್ತವೆ ಮತ್ತು 90 0 ಕೋನದಲ್ಲಿ ಪರಸ್ಪರ ಛೇದಿಸುವ ಧ್ರುವದಲ್ಲಿ ಲಂಬವಾಗಿರುತ್ತವೆ. ಒಂದೇ ಸಮತಲದಲ್ಲಿ ಎರಡು ಸಮಾನಾಂತರ ರೇಖೆಗಳು ಛೇದಿಸುವುದಿಲ್ಲ, ಆದರೆ ಧ್ರುವದಲ್ಲಿ ಲಂಬವಾಗಿರಬಹುದು ಎಂದು ಅದು ತಿರುಗುತ್ತದೆ.

ಸಹಜವಾಗಿ, ಅಂತಹ ತ್ರಿಕೋನದ ಬದಿಗಳು ನೇರ ರೇಖೆಗಳಾಗಿರುವುದಿಲ್ಲ, ಆದರೆ ಪೀನ, ಗೋಳಾಕಾರದ ಆಕಾರವನ್ನು ಪುನರಾವರ್ತಿಸುತ್ತದೆ ಗ್ಲೋಬ್. ಆದರೆ ಇದು ನಿಖರವಾಗಿ ಬಾಹ್ಯಾಕಾಶದ ನೈಜ ಪ್ರಪಂಚವಾಗಿದೆ.

ನೈಜ ಜಾಗದ ಜ್ಯಾಮಿತಿ, 19 ನೇ ಶತಮಾನದ ಮಧ್ಯದಲ್ಲಿ ಅದರ ವಕ್ರತೆಯನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಜರ್ಮನ್ ಗಣಿತಜ್ಞ ಬಿ. ರೀಮನ್ (1820-1866) ಅಭಿವೃದ್ಧಿಪಡಿಸಿದರು. ಆದರೆ ಈ ಬಗ್ಗೆ ಶಾಲಾ ಮಕ್ಕಳಿಗೆ ಹೇಳಿಲ್ಲ.

ಆದ್ದರಿಂದ, ಯೂಕ್ಲಿಡಿಯನ್ ರೇಖಾಗಣಿತವು ಭೂಮಿಯ ರೂಪವನ್ನು ಸಮತಲ ಮೇಲ್ಮೈಯೊಂದಿಗೆ ಸಮತಟ್ಟಾಗಿ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ, ಅದು ವಾಸ್ತವವಾಗಿ ಅಲ್ಲ, ಇದು ಸಿಮ್ಯುಲಾಕ್ರಮ್ ಆಗಿದೆ. ನೂಟಿಕ್ ಎಂಬುದು ರೀಮನ್ನಿಯನ್ ರೇಖಾಗಣಿತವಾಗಿದ್ದು ಅದು ಜಾಗದ ವಕ್ರತೆಯನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ. ಅದರಲ್ಲಿರುವ ತ್ರಿಕೋನದ ಆಂತರಿಕ ಕೋನಗಳ ಮೊತ್ತವು 180 0 ಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ.

ಪುರಾವೆ

ಅವಕಾಶ ABC" - ಅನಿಯಂತ್ರಿತ ತ್ರಿಕೋನ. ಮೇಲ್ಭಾಗದ ಮೂಲಕ ಮುನ್ನಡೆಸೋಣ ಬಿ ಸಾಲಿಗೆ ಸಮಾನಾಂತರವಾದ ಸಾಲುಎ.ಸಿ. (ಅಂತಹ ಸರಳ ರೇಖೆಯನ್ನು ಯೂಕ್ಲಿಡಿಯನ್ ನೇರ ರೇಖೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ). ಅದರ ಮೇಲೆ ಒಂದು ಬಿಂದುವನ್ನು ಗುರುತಿಸೋಣಡಿ ಆದ್ದರಿಂದ ಅಂಕಗಳುಎ ಮತ್ತುಡಿ ನೇರ ರೇಖೆಯ ವಿರುದ್ಧ ಬದಿಗಳಲ್ಲಿ ಇರಿಸಿ ಬಿ.ಸಿ..ಕೋನಗಳು DBCಮತ್ತು ಎಸಿಬಿಒಂದು ಸೆಕೆಂಟ್‌ನಿಂದ ರೂಪುಗೊಂಡ ಆಂತರಿಕ ಅಡ್ಡಹಾಯುವಿಕೆಯಂತೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಬಿ.ಸಿ.ಸಮಾನಾಂತರ ರೇಖೆಗಳೊಂದಿಗೆ ಎ.ಸಿ.ಮತ್ತು ಬಿಡಿ. ಆದ್ದರಿಂದ, ಶೃಂಗಗಳಲ್ಲಿ ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತ ಬಿಮತ್ತು ಇದರೊಂದಿಗೆಕೋನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಎಬಿಡಿ.ತ್ರಿಕೋನದ ಎಲ್ಲಾ ಮೂರು ಕೋನಗಳ ಮೊತ್ತವು ಕೋನಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಎಬಿಡಿಮತ್ತು BAC. ಈ ಕೋನಗಳು ಸಮಾನಾಂತರವಾಗಿ ಆಂತರಿಕ ಏಕಪಕ್ಷೀಯವಾದವುಗಳಾಗಿರುವುದರಿಂದ ಎ.ಸಿ.ಮತ್ತು ಬಿಡಿಸೆಕೆಂಟ್ ನಲ್ಲಿ ಎಬಿ, ಆಗ ಅವುಗಳ ಮೊತ್ತ 180°. ಪ್ರಮೇಯವು ಸಾಬೀತಾಗಿದೆ.

ಪರಿಣಾಮಗಳು

ಪ್ರಮೇಯದಿಂದ ಯಾವುದೇ ತ್ರಿಕೋನವು ಎರಡು ತೀವ್ರ ಕೋನಗಳನ್ನು ಹೊಂದಿದೆ ಎಂದು ಅನುಸರಿಸುತ್ತದೆ. ವಾಸ್ತವವಾಗಿ, ವಿರೋಧಾಭಾಸದ ಮೂಲಕ ಪುರಾವೆಯನ್ನು ಬಳಸಿ, ತ್ರಿಕೋನವು ಕೇವಲ ಒಂದು ತೀವ್ರ ಕೋನವನ್ನು ಹೊಂದಿದೆ ಅಥವಾ ಯಾವುದೇ ತೀವ್ರ ಕೋನಗಳನ್ನು ಹೊಂದಿಲ್ಲ ಎಂದು ನಾವು ಊಹಿಸೋಣ. ನಂತರ ಈ ತ್ರಿಕೋನವು ಕನಿಷ್ಟ ಎರಡು ಕೋನಗಳನ್ನು ಹೊಂದಿರುತ್ತದೆ, ಪ್ರತಿಯೊಂದೂ ಕನಿಷ್ಠ 90 ° ಆಗಿದೆ. ಈ ಕೋನಗಳ ಮೊತ್ತವು 180 ° ಗಿಂತ ಕಡಿಮೆಯಿಲ್ಲ. ಆದರೆ ಇದು ಅಸಾಧ್ಯ, ಏಕೆಂದರೆ ತ್ರಿಕೋನದ ಎಲ್ಲಾ ಕೋನಗಳ ಮೊತ್ತವು 180 ° ಆಗಿದೆ. ಕ್ಯೂ.ಇ.ಡಿ.

ಸಿಂಪ್ಲೆಕ್ಸ್ ಸಿದ್ಧಾಂತಕ್ಕೆ ಸಾಮಾನ್ಯೀಕರಣ

ಸಿಂಪ್ಲೆಕ್ಸ್‌ನ i ಮತ್ತು j ಮುಖಗಳ ನಡುವಿನ ಕೋನ ಎಲ್ಲಿದೆ.

ಟಿಪ್ಪಣಿಗಳು

• ಗೋಳದ ಮೇಲೆ, ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತವು ಯಾವಾಗಲೂ 180 ° ಮೀರಿದೆ, ವ್ಯತ್ಯಾಸವನ್ನು ಗೋಳಾಕಾರದ ಹೆಚ್ಚುವರಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ತ್ರಿಕೋನದ ಪ್ರದೇಶಕ್ಕೆ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ.
• ಲೋಬಚೆವ್ಸ್ಕಿ ಸಮತಲದಲ್ಲಿ, ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತವು ಯಾವಾಗಲೂ 180 ° ಗಿಂತ ಕಡಿಮೆಯಿರುತ್ತದೆ. ವ್ಯತ್ಯಾಸವು ತ್ರಿಕೋನದ ಪ್ರದೇಶಕ್ಕೆ ಅನುಪಾತದಲ್ಲಿರುತ್ತದೆ.

ಸಹ ನೋಡಿ

ವಿಕಿಮೀಡಿಯಾ ಫೌಂಡೇಶನ್. 2010.

ಇತರ ನಿಘಂಟುಗಳಲ್ಲಿ "ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತದ ಪ್ರಮೇಯ" ಏನೆಂದು ನೋಡಿ:

ಯೂಕ್ಲಿಡಿಯನ್ ರೇಖಾಗಣಿತದಲ್ಲಿ ಬಹುಭುಜಾಕೃತಿಗಳ ಗುಣಲಕ್ಷಣ: ತ್ರಿಕೋನದ n ಕೋನಗಳ ಮೊತ್ತವು 180 ° (n 2). ಪರಿವಿಡಿ 1 ಪುರಾವೆ 2 ಟಿಪ್ಪಣಿ ... ವಿಕಿಪೀಡಿಯಾ

ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯವು ಯೂಕ್ಲಿಡಿಯನ್ ರೇಖಾಗಣಿತದ ಮೂಲಭೂತ ಪ್ರಮೇಯಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ, ಇದು ಲಂಬ ತ್ರಿಕೋನದ ಬದಿಗಳ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ಸ್ಥಾಪಿಸುತ್ತದೆ. ಪರಿವಿಡಿ 1 ... ವಿಕಿಪೀಡಿಯಾ

ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯವು ಯೂಕ್ಲಿಡಿಯನ್ ರೇಖಾಗಣಿತದ ಮೂಲಭೂತ ಪ್ರಮೇಯಗಳಲ್ಲಿ ಒಂದಾಗಿದೆ, ಇದು ಲಂಬ ತ್ರಿಕೋನದ ಬದಿಗಳ ನಡುವಿನ ಸಂಬಂಧವನ್ನು ಸ್ಥಾಪಿಸುತ್ತದೆ. ಪರಿವಿಡಿ 1 ಹೇಳಿಕೆಗಳು 2 ಸಾಕ್ಷಿ ... ವಿಕಿಪೀಡಿಯಾ

ಕೊಸೈನ್ ಪ್ರಮೇಯವು ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯದ ಸಾಮಾನ್ಯೀಕರಣವಾಗಿದೆ. ತ್ರಿಕೋನದ ಒಂದು ಬದಿಯ ಚೌಕವು ಅದರ ಎರಡು ಬದಿಗಳ ಚೌಕಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಕೋನದ ಕೊಸೈನ್‌ನಿಂದ ಈ ಬದಿಗಳ ಎರಡು ಪಟ್ಟು ಉತ್ಪನ್ನವಾಗಿದೆ. ಇದರೊಂದಿಗೆ ಸಮತಲ ತ್ರಿಕೋನಕ್ಕಾಗಿ ಬದಿಗಳು a,b,cಮತ್ತು ಕೋನ α... ... ವಿಕಿಪೀಡಿಯಾ

ಈ ಪದವು ಇತರ ಅರ್ಥಗಳನ್ನು ಹೊಂದಿದೆ, ತ್ರಿಕೋನ (ಅರ್ಥಗಳು) ನೋಡಿ. ತ್ರಿಕೋನ (ಯೂಕ್ಲಿಡಿಯನ್ ಜಾಗದಲ್ಲಿ) ಆಗಿದೆ ಜ್ಯಾಮಿತೀಯ ಚಿತ್ರ, ಒಂದೇ ನೇರ ರೇಖೆಯಲ್ಲಿ ಇರದ ಮೂರು ಬಿಂದುಗಳನ್ನು ಸಂಪರ್ಕಿಸುವ ಮೂರು ವಿಭಾಗಗಳಿಂದ ರಚಿಸಲಾಗಿದೆ. ಮೂರು ಚುಕ್ಕೆಗಳು,... ... ವಿಕಿಪೀಡಿಯಾ

ಪ್ರಮಾಣಿತ ಸಂಕೇತ ತ್ರಿಕೋನವು 3 ಶೃಂಗಗಳು (ಕೋನಗಳು) ಮತ್ತು 3 ಬದಿಗಳನ್ನು ಹೊಂದಿರುವ ಸರಳ ಬಹುಭುಜಾಕೃತಿಯಾಗಿದೆ; ಸಮತಲದ ಭಾಗವು ಒಂದೇ ಸಾಲಿನಲ್ಲಿ ಇರದ ಮೂರು ಬಿಂದುಗಳಿಂದ ಸುತ್ತುವರೆದಿದೆ ಮತ್ತು ಈ ಬಿಂದುಗಳನ್ನು ಜೋಡಿಯಾಗಿ ಸಂಪರ್ಕಿಸುವ ಮೂರು ವಿಭಾಗಗಳು. ತ್ರಿಕೋನದ ಶೃಂಗಗಳು ... ವಿಕಿಪೀಡಿಯಾ

ಪ್ರಾಚೀನ ಗ್ರೀಕ್ ಗಣಿತಜ್ಞ. 3 ನೇ ಶತಮಾನದಲ್ಲಿ ಅಲೆಕ್ಸಾಂಡ್ರಿಯಾದಲ್ಲಿ ಕೆಲಸ ಮಾಡಿದರು. ಕ್ರಿ.ಪೂ ಇ. ಮುಖ್ಯ ಕೃತಿ "ಪ್ರಿನ್ಸಿಪಿಯಾ" (15 ಪುಸ್ತಕಗಳು), ಪುರಾತನ ಗಣಿತಶಾಸ್ತ್ರ, ಪ್ರಾಥಮಿಕ ಜ್ಯಾಮಿತಿ, ಸಂಖ್ಯಾ ಸಿದ್ಧಾಂತ, ಸಾಮಾನ್ಯ ಸಿದ್ಧಾಂತಪ್ರದೇಶಗಳು ಮತ್ತು ಸಂಪುಟಗಳನ್ನು ನಿರ್ಧರಿಸಲು ಸಂಬಂಧಗಳು ಮತ್ತು ವಿಧಾನಗಳು,... ... ವಿಶ್ವಕೋಶ ನಿಘಂಟು

- (ಕ್ರಿ.ಪೂ. 275 ಮತ್ತು 270 ರ ನಡುವೆ ನಿಧನರಾದರು) ಪ್ರಾಚೀನ ಗ್ರೀಕ್ ಗಣಿತಜ್ಞ. ಅವನ ಹುಟ್ಟಿದ ಸಮಯ ಮತ್ತು ಸ್ಥಳದ ಬಗ್ಗೆ ಮಾಹಿತಿಯು ನಮಗೆ ತಲುಪಿಲ್ಲ, ಆದರೆ ಯೂಕ್ಲಿಡ್ ಅಲೆಕ್ಸಾಂಡ್ರಿಯಾದಲ್ಲಿ ವಾಸಿಸುತ್ತಿದ್ದನೆಂದು ತಿಳಿದಿದೆ ಮತ್ತು ಅವನ ಚಟುವಟಿಕೆಯ ಉತ್ತುಂಗವು ಈಜಿಪ್ಟ್‌ನಲ್ಲಿ ಟಾಲೆಮಿ I ರ ಆಳ್ವಿಕೆಯಲ್ಲಿ ಸಂಭವಿಸಿತು ... ... ಬಿಗ್ ಎನ್ಸೈಕ್ಲೋಪೀಡಿಕ್ ಡಿಕ್ಷನರಿ

ಯೂಕ್ಲಿಡಿಯನ್ ಜ್ಯಾಮಿತಿಯನ್ನು ಹೋಲುವ ರೇಖಾಗಣಿತವು ಅಂಕಿಗಳ ಚಲನೆಯನ್ನು ವ್ಯಾಖ್ಯಾನಿಸುತ್ತದೆ, ಆದರೆ ಯೂಕ್ಲಿಡಿಯನ್ ಜ್ಯಾಮಿತಿಯಿಂದ ಭಿನ್ನವಾಗಿದೆ, ಅದರ ಐದು ಪೋಸ್ಟ್ಯುಲೇಟ್‌ಗಳಲ್ಲಿ ಒಂದನ್ನು (ಎರಡನೇ ಅಥವಾ ಐದನೇ) ಅದರ ನಿರಾಕರಣೆಯಿಂದ ಬದಲಾಯಿಸಲಾಗುತ್ತದೆ. ಯೂಕ್ಲಿಡಿಯನ್ ತತ್ವಗಳಲ್ಲಿ ಒಂದರ ನಿರಾಕರಣೆ... ... ಕೊಲಿಯರ್ಸ್ ಎನ್ಸೈಕ್ಲೋಪೀಡಿಯಾ

ತ್ರಿಕೋನ . ತೀಕ್ಷ್ಣವಾದ, ಚೂಪಾದ ಮತ್ತು ಬಲ ತ್ರಿಕೋನ.

ಕಾಲುಗಳು ಮತ್ತು ಹೈಪೊಟೆನ್ಯೂಸ್. ಐಸೊಸೆಲ್ಸ್ ಮತ್ತು ಸಮಬಾಹು ತ್ರಿಕೋನ.

ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತ.

ತ್ರಿಕೋನದ ಬಾಹ್ಯ ಕೋನ. ತ್ರಿಕೋನಗಳ ಸಮಾನತೆಯ ಚಿಹ್ನೆಗಳು.

ತ್ರಿಕೋನದಲ್ಲಿ ಗಮನಾರ್ಹವಾದ ರೇಖೆಗಳು ಮತ್ತು ಬಿಂದುಗಳು: ಎತ್ತರಗಳು, ಮಧ್ಯಗಳು,

ದ್ವಿಭಾಜಕಗಳು, ಮಧ್ಯಮಇ ಲಂಬವಾಗಿ, ಆರ್ಥೋಸೆಂಟರ್,

ಗುರುತ್ವಾಕರ್ಷಣೆಯ ಕೇಂದ್ರ, ಸುತ್ತುವರಿದ ವೃತ್ತದ ಕೇಂದ್ರ, ಕೆತ್ತಲಾದ ವೃತ್ತದ ಕೇಂದ್ರ.

ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯ. ಅನಿಯಂತ್ರಿತ ತ್ರಿಕೋನದಲ್ಲಿ ಆಕಾರ ಅನುಪಾತ.

ತ್ರಿಕೋನ ಮೂರು ಬದಿಗಳನ್ನು (ಅಥವಾ ಮೂರು ಕೋನಗಳು) ಹೊಂದಿರುವ ಬಹುಭುಜಾಕೃತಿಯಾಗಿದೆ. ತ್ರಿಕೋನದ ಬದಿಗಳನ್ನು ಹೆಚ್ಚಾಗಿ ಸಣ್ಣ ಅಕ್ಷರಗಳಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ, ಅದು ವಿರುದ್ಧ ಶೃಂಗಗಳನ್ನು ಪ್ರತಿನಿಧಿಸುವ ದೊಡ್ಡ ಅಕ್ಷರಗಳಿಗೆ ಅನುಗುಣವಾಗಿರುತ್ತದೆ.

ಎಲ್ಲಾ ಮೂರು ಕೋನಗಳು ತೀವ್ರವಾಗಿದ್ದರೆ (ಚಿತ್ರ 20), ನಂತರ ಇದು ತೀವ್ರ ತ್ರಿಕೋನ . ಒಂದು ಕೋನವು ಸರಿಯಾಗಿದ್ದರೆ(C, Fig.21), ಅದು ಬಲ ತ್ರಿಕೋನ; ಬದಿಗಳುa, bಲಂಬ ಕೋನವನ್ನು ರೂಪಿಸುವುದನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಕಾಲುಗಳು; ಬದಿಸಿಲಂಬ ಕೋನದ ಎದುರು ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಹೈಪೊಟೆನ್ಯೂಸ್. ಒಂದು ವೇಳೆಚೂಪಾದ ಕೋನಗಳು (ಬಿ, ಚಿತ್ರ 22), ಅದು ಚೂಪಾದ ತ್ರಿಕೋನ.


ತ್ರಿಕೋನ ABC (ಚಿತ್ರ 23) - ಸಮದ್ವಿಬಾಹುಗಳು, ವೇಳೆ ಎರಡುಅದರ ಬದಿಗಳು ಸಮಾನವಾಗಿವೆ (ಎ= ಸಿ); ಈ ಸಮಾನ ಬದಿಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಪಾರ್ಶ್ವದ, ಮೂರನೇ ವ್ಯಕ್ತಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಆಧಾರದತ್ರಿಕೋನ. ತ್ರಿಕೋನ ABC (ಚಿತ್ರ 24) - ಸಮಬಾಹು, ಒಂದು ವೇಳೆ ಎಲ್ಲಾಅದರ ಬದಿಗಳು ಸಮಾನವಾಗಿವೆ (ಎ = ಬಿ = ಸಿ) ಸಾಮಾನ್ಯವಾಗಿ ( ಎ ≠ ಬಿ ≠ ಸಿ) ನಾವು ಹೊಂದಿದ್ದೇವೆ ಸ್ಕೇಲೆನ್ತ್ರಿಕೋನ .

ತ್ರಿಕೋನಗಳ ಮೂಲ ಗುಣಲಕ್ಷಣಗಳು. ಯಾವುದೇ ತ್ರಿಕೋನದಲ್ಲಿ:

1. ದೊಡ್ಡ ಬದಿಯ ಎದುರು ದೊಡ್ಡ ಕೋನವಿದೆ, ಮತ್ತು ಪ್ರತಿಯಾಗಿ.

2. ಸಮಾನ ಕೋನಗಳು ಸಮಾನ ಬದಿಗಳಿಗೆ ವಿರುದ್ಧವಾಗಿರುತ್ತವೆ ಮತ್ತು ಪ್ರತಿಯಾಗಿ.

ನಿರ್ದಿಷ್ಟವಾಗಿ, ಎಲ್ಲಾ ಕೋನಗಳು ಸಮಬಾಹುತ್ರಿಕೋನ ಸಮಾನವಾಗಿರುತ್ತದೆ.

3. ತ್ರಿಕೋನದ ಕೋನಗಳ ಮೊತ್ತವು 180 ಆಗಿದೆ º .

ಕೊನೆಯ ಎರಡು ಗುಣಲಕ್ಷಣಗಳಿಂದ ಇದು ಸಮಬಾಹುದಲ್ಲಿ ಪ್ರತಿ ಕೋನವನ್ನು ಅನುಸರಿಸುತ್ತದೆ

ತ್ರಿಕೋನವು 60 ಆಗಿದೆ º.

4. ತ್ರಿಕೋನದ ಬದಿಗಳಲ್ಲಿ ಒಂದನ್ನು ಮುಂದುವರಿಸುವುದು (AC, ಚಿತ್ರ 25), ನಾವು ಪಡೆಯುತ್ತೇವೆ ಬಾಹ್ಯ

ಕೋನ BCD . ತ್ರಿಕೋನದ ಬಾಹ್ಯ ಕೋನವು ಆಂತರಿಕ ಕೋನಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ,

ಅದರ ಪಕ್ಕದಲ್ಲಿಲ್ಲ : BCD = A + B.

5. ಯಾವುದಾದರು ತ್ರಿಕೋನದ ಬದಿಯು ಇತರ ಎರಡು ಬದಿಗಳ ಮೊತ್ತಕ್ಕಿಂತ ಕಡಿಮೆ ಮತ್ತು ದೊಡ್ಡದಾಗಿದೆ

ಅವರ ವ್ಯತ್ಯಾಸಗಳು (ಎ < ಬಿ + ಸಿ, ಎ > ಬಿ – ಸಿ;ಬಿ < ಎ + ಸಿ, ಬಿ > ಎ – ಸಿ;ಸಿ < ಎ + ಬಿ,ಸಿ > ಎ – ಬಿ).

ತ್ರಿಕೋನಗಳ ಸಮಾನತೆಯ ಚಿಹ್ನೆಗಳು.

ತ್ರಿಕೋನಗಳು ಅನುಕ್ರಮವಾಗಿ ಸಮಾನವಾಗಿದ್ದರೆ ಅವು ಸರ್ವಸಮಾನವಾಗಿರುತ್ತವೆ:

ಎ ) ಎರಡು ಬದಿಗಳು ಮತ್ತು ಅವುಗಳ ನಡುವಿನ ಕೋನ;

ಬಿ ) ಎರಡು ಮೂಲೆಗಳು ಮತ್ತು ಅವುಗಳ ಪಕ್ಕದ ಬದಿ;

ಸಿ) ಮೂರು ಬದಿಗಳು.

ಬಲ ತ್ರಿಕೋನಗಳ ಸಮಾನತೆಯ ಚಿಹ್ನೆಗಳು.

ಎರಡು ಆಯತಾಕಾರದಕೆಳಗಿನ ಷರತ್ತುಗಳಲ್ಲಿ ಒಂದನ್ನು ಪೂರೈಸಿದರೆ ತ್ರಿಕೋನಗಳು ಸಮಾನವಾಗಿರುತ್ತದೆ:

1) ಅವರ ಕಾಲುಗಳು ಸಮಾನವಾಗಿವೆ;

2) ಒಂದು ತ್ರಿಕೋನದ ಲೆಗ್ ಮತ್ತು ಹೈಪೊಟೆನ್ಯೂಸ್ ಇತರ ಲೆಗ್ ಮತ್ತು ಹೈಪೋಟೆನ್ಯೂಸ್ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ;

3) ಒಂದು ತ್ರಿಕೋನದ ಹೈಪೊಟೆನ್ಯೂಸ್ ಮತ್ತು ತೀವ್ರ ಕೋನವು ಇನ್ನೊಂದರ ಹೈಪೊಟೆನ್ಯೂಸ್ ಮತ್ತು ತೀವ್ರ ಕೋನಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ;

4) ಕಾಲು ಮತ್ತು ಒಂದು ತ್ರಿಕೋನದ ಪಕ್ಕದ ತೀವ್ರ ಕೋನವು ಲೆಗ್ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ಇನ್ನೊಂದರ ಪಕ್ಕದ ತೀವ್ರ ಕೋನ;

5) ಕಾಲು ಮತ್ತು ಒಂದು ತ್ರಿಕೋನದ ವಿರುದ್ಧ ತೀವ್ರವಾದ ಕೋನವು ಲೆಗ್ಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ಮತ್ತು ಇನ್ನೊಂದರ ವಿರುದ್ಧ ತೀವ್ರ ಕೋನ.

ತ್ರಿಕೋನದಲ್ಲಿ ಅದ್ಭುತ ರೇಖೆಗಳು ಮತ್ತು ಬಿಂದುಗಳು.

ಎತ್ತರ ತ್ರಿಕೋನವಾಗಿದೆಲಂಬವಾಗಿ,ಯಾವುದೇ ಶೃಂಗದಿಂದ ಎದುರು ಭಾಗಕ್ಕೆ ಇಳಿಸಲಾಗಿದೆ ( ಅಥವಾ ಅದರ ಮುಂದುವರಿಕೆ). ಈ ಭಾಗವನ್ನು ಕರೆಯಲಾಗುತ್ತದೆತ್ರಿಕೋನದ ಆಧಾರ . ತ್ರಿಕೋನದ ಮೂರು ಎತ್ತರಗಳು ಯಾವಾಗಲೂ ಛೇದಿಸುತ್ತವೆಒಂದು ಹಂತದಲ್ಲಿ, ಎಂದು ಕರೆಯುತ್ತಾರೆ ಆರ್ಥೋಸೆಂಟರ್ತ್ರಿಕೋನ. ತೀವ್ರ ತ್ರಿಕೋನದ ಆರ್ಥೋಸೆಂಟರ್ (ಪಾಯಿಂಟ್ಓ , ಚಿತ್ರ 26) ತ್ರಿಕೋನದ ಒಳಗೆ ಇದೆ, ಮತ್ತುಚೂಪಾದ ತ್ರಿಕೋನದ ಆರ್ಥೋಸೆಂಟರ್ (ಪಾಯಿಂಟ್ಓ , ಚಿತ್ರ.27) – ಹೊರಗೆ; ಲಂಬ ತ್ರಿಕೋನದ ಆರ್ಥೋಸೆಂಟರ್ ಬಲ ಕೋನದ ಶೃಂಗದೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ.

ಮಧ್ಯಮ - ಇದು ಸಾಲಿನ ವಿಭಾಗ , ತ್ರಿಕೋನದ ಯಾವುದೇ ಶೃಂಗವನ್ನು ಎದುರು ಭಾಗದ ಮಧ್ಯಕ್ಕೆ ಸಂಪರ್ಕಿಸುವುದು. ತ್ರಿಕೋನದ ಮೂರು ಮಧ್ಯಭಾಗಗಳು (AD, BE, CF, fig.28) ಒಂದು ಹಂತದಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ ಓ , ಯಾವಾಗಲೂ ತ್ರಿಕೋನದೊಳಗೆ ಮಲಗಿರುತ್ತದೆಮತ್ತು ಅವನಾಗಿರುವುದು ಗುರುತ್ವಾಕರ್ಷಣೆಯ ಕೇಂದ್ರ. ಈ ಬಿಂದು ಪ್ರತಿ ಮಧ್ಯವನ್ನು 2:1 ರ ಅನುಪಾತದಲ್ಲಿ ಭಾಗಿಸುತ್ತದೆ, ಶೃಂಗದಿಂದ ಎಣಿಸುತ್ತದೆ.

ಬೈಸೆಕ್ಟರ್ - ಇದು ದ್ವಿಭಾಜಕ ವಿಭಾಗಶೃಂಗದಿಂದ ಬಿಂದುವಿಗೆ ಕೋನ ಎದುರು ಭಾಗದೊಂದಿಗೆ ಛೇದಕಗಳು. ತ್ರಿಕೋನದ ಮೂರು ದ್ವಿಭಾಜಕಗಳು (AD, BE, CF, fig.29) ಒಂದು ಹಂತದಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ ಓಹ್, ಯಾವಾಗಲೂ ತ್ರಿಕೋನದೊಳಗೆ ಮಲಗಿರುತ್ತದೆಮತ್ತು ಇರುವುದು ಕೆತ್ತಲಾದ ವೃತ್ತದ ಮಧ್ಯಭಾಗ(ವಿಭಾಗವನ್ನು ನೋಡಿ "ಕೆತ್ತಲಾಗಿದೆಮತ್ತು ಸುತ್ತುವರಿದ ಬಹುಭುಜಾಕೃತಿಗಳು").

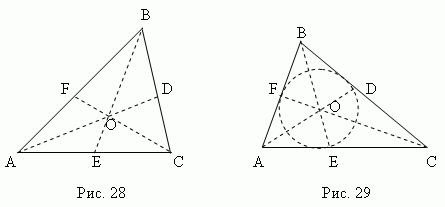
ದ್ವಿಭಾಜಕವು ಎದುರು ಭಾಗವನ್ನು ಪಕ್ಕದ ಬದಿಗಳಿಗೆ ಅನುಪಾತದಲ್ಲಿ ಭಾಗಗಳಾಗಿ ವಿಭಜಿಸುತ್ತದೆ ; ಉದಾಹರಣೆಗೆ, ಚಿತ್ರ 29 ರಲ್ಲಿ AE: CE = AB: BC.

ಮಧ್ಯದ ಲಂಬ ಮಧ್ಯದಿಂದ ಎಳೆಯಲಾದ ಲಂಬವಾಗಿದೆವಿಭಾಗದ ಬಿಂದುಗಳು (ಬದಿಗಳು). ತ್ರಿಕೋನ ABC ಯ ಮೂರು ಲಂಬ ದ್ವಿಭಾಜಕಗಳು(KO, MO, NO, ಚಿತ್ರ 30 ) O ಒಂದು ಹಂತದಲ್ಲಿ ಛೇದಿಸುತ್ತದೆ, ಅದು ಕೇಂದ್ರ ಸುತ್ತುವರಿದ ವೃತ್ತ (ಅಂಕಗಳು ಕೆ, ಎಂ, ಎನ್ - ತ್ರಿಕೋನದ ಬದಿಗಳ ಮಧ್ಯಬಿಂದುಗಳುಎಬಿಸಿ).

ತೀವ್ರವಾದ ತ್ರಿಕೋನದಲ್ಲಿ, ಈ ಬಿಂದುವು ತ್ರಿಕೋನದ ಒಳಗೆ ಇರುತ್ತದೆ; ಮಬ್ಬಾಗಿ - ಹೊರಗೆ; ಒಂದು ಆಯತಾಕಾರದಲ್ಲಿ - ಹೈಪೊಟೆನ್ಯೂಸ್ ಮಧ್ಯದಲ್ಲಿ. ಆರ್ಥೋಸೆಂಟರ್, ಗುರುತ್ವಾಕರ್ಷಣೆಯ ಕೇಂದ್ರ, ಸುತ್ತಳತೆ ಮತ್ತು ಕೆತ್ತಲಾದ ವೃತ್ತ ಸಮಬಾಹು ತ್ರಿಕೋನದಲ್ಲಿ ಮಾತ್ರ ಸೇರಿಕೊಳ್ಳುತ್ತದೆ.

ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯ. ಲಂಬ ತ್ರಿಕೋನದಲ್ಲಿ, ಉದ್ದದ ಚೌಕಹೈಪೊಟೆನ್ಯೂಸ್ ಕಾಲುಗಳ ಉದ್ದದ ಚೌಕಗಳ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ಪೈಥಾಗರಿಯನ್ ಪ್ರಮೇಯದ ಪುರಾವೆಯು ಚಿತ್ರ 31 ರಿಂದ ಸ್ಪಷ್ಟವಾಗಿ ಅನುಸರಿಸುತ್ತದೆ. ಬಲ ತ್ರಿಕೋನವನ್ನು ಪರಿಗಣಿಸಿಕಾಲುಗಳೊಂದಿಗೆ ಎಬಿಸಿ a, bಮತ್ತು ಹೈಪೊಟೆನ್ಯೂಸ್ ಸಿ.

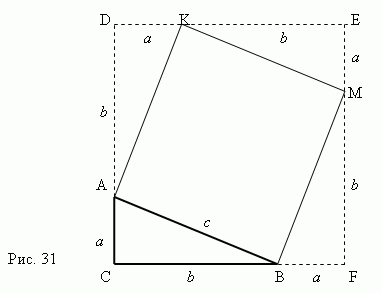
ಚೌಕವನ್ನು ನಿರ್ಮಿಸೋಣಎಕೆಎಂಬಿ ಹೈಪೊಟೆನ್ಯೂಸ್ ಅನ್ನು ಬಳಸುವುದುಎಬಿ ಒಂದು ಕಡೆಯಾಗಿ. ನಂತರಬಲ ತ್ರಿಕೋನದ ಬದಿಗಳನ್ನು ಮುಂದುವರಿಸಿಎಬಿಸಿ ಆದ್ದರಿಂದ ಒಂದು ಚೌಕವನ್ನು ಪಡೆಯಲು CDEF , ಯಾರ ಬದಿಯು ಸಮಾನವಾಗಿರುತ್ತದೆa + b.ಚೌಕದ ಪ್ರದೇಶವು ಈಗ ಸ್ಪಷ್ಟವಾಗಿದೆ CDEF ಇದಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ ( a+b) 2 . ಮತ್ತೊಂದೆಡೆ, ಇದು ಪ್ರದೇಶವು ಮೊತ್ತಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆಪ್ರದೇಶಗಳು ನಾಲ್ಕು ಬಲ ತ್ರಿಕೋನಗಳುಮತ್ತು ಚದರ AKMB, ಅಂದರೆ

ಸಿ 2 + 4 (ab / 2) = ಸಿ 2 + 2 ab,

ಇಲ್ಲಿಂದ,

ಸಿ 2 + 2 ab= (a+b) 2 ,

ಮತ್ತು ಅಂತಿಮವಾಗಿ ನಾವು ಹೊಂದಿದ್ದೇವೆ:

ಸಿ 2 =ಎ 2 +b 2 .

ಅನಿಯಂತ್ರಿತ ತ್ರಿಕೋನದಲ್ಲಿ ಆಕಾರ ಅನುಪಾತ.

ಸಾಮಾನ್ಯ ಸಂದರ್ಭದಲ್ಲಿ (ಅನಿಯಂತ್ರಿತ ತ್ರಿಕೋನಕ್ಕಾಗಿ) ನಾವು ಹೊಂದಿದ್ದೇವೆ:

ಸಿ 2 =ಎ 2 +b 2 – 2ab· cos ಸಿ,

ಅಲ್ಲಿ ಸಿ - ಬದಿಗಳ ನಡುವಿನ ಕೋನಎಮತ್ತು ಬಿ .