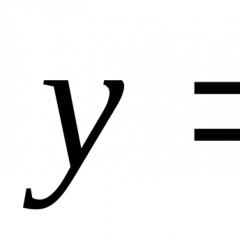ಬಹು ಆಯಾಮದ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಳು. ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಳ ಸಿದ್ಧಾಂತದ ವಿಧಾನಗಳು. ಡಿಸ್ಕ್ರೀಟ್ ಮಾರ್ಕೊವ್ ಸರಪಳಿಗಳು. ಉದಾಹರಣೆ

ಸೂಕ್ತವಾದ ಪರಿಹಾರವನ್ನು ಆಯ್ಕೆಮಾಡುವಾಗ ವಿಶ್ಲೇಷಿಸಬೇಕಾದ ಅನೇಕ ಕಾರ್ಯಾಚರಣೆಗಳು ಹಲವಾರು ಯಾದೃಚ್ಛಿಕ ಅಂಶಗಳ ಆಧಾರದ ಮೇಲೆ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳಾಗಿ ಅಭಿವೃದ್ಧಿಗೊಳ್ಳುತ್ತವೆ.

ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯ ರೂಪದಲ್ಲಿ ಅಭಿವೃದ್ಧಿಗೊಳ್ಳುವ ಅನೇಕ ಕಾರ್ಯಾಚರಣೆಗಳ ಗಣಿತದ ವಿವರಣೆಗಾಗಿ, ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳು ಎಂದು ಕರೆಯಲ್ಪಡುವ ಸಂಭವನೀಯತೆ ಸಿದ್ಧಾಂತದಲ್ಲಿ ಅಭಿವೃದ್ಧಿಪಡಿಸಲಾದ ಗಣಿತದ ಉಪಕರಣವನ್ನು ಯಶಸ್ವಿಯಾಗಿ ಅನ್ವಯಿಸಬಹುದು.

ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯ ಪರಿಕಲ್ಪನೆಯನ್ನು ನಾವು ವಿವರಿಸೋಣ.

ಏನಾದರೂ ವ್ಯವಸ್ಥೆ ಇರಲಿ ಎಸ್,ಅವರ ಸ್ಥಿತಿಯು ಕಾಲಾನಂತರದಲ್ಲಿ ಬದಲಾಗುತ್ತದೆ (ವ್ಯವಸ್ಥೆಯ ಅಡಿಯಲ್ಲಿ ಎಸ್ಯಾವುದನ್ನಾದರೂ ಅರ್ಥೈಸಬಹುದು: ಕೈಗಾರಿಕಾ ಉದ್ಯಮ, ತಾಂತ್ರಿಕ ಸಾಧನ, ದುರಸ್ತಿ ಅಂಗಡಿ, ಇತ್ಯಾದಿ). ಸಿಸ್ಟಮ್ ಸ್ಟೇಟ್ ಇದ್ದರೆ ಎಸ್ಕಾಲಾನಂತರದಲ್ಲಿ ಯಾದೃಚ್ಛಿಕವಾಗಿ, ಅನಿರೀಕ್ಷಿತ ರೀತಿಯಲ್ಲಿ ಮುಂಚಿತವಾಗಿ ಬದಲಾವಣೆಗಳು, ಅವರು ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಹೇಳುತ್ತಾರೆ ಎಸ್ಸೋರಿಕೆಯಾಗುತ್ತದೆ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆ.

ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳ ಉದಾಹರಣೆಗಳು:

ಷೇರು ಮಾರುಕಟ್ಟೆಯಲ್ಲಿ ಬೆಲೆ ಏರಿಳಿತ;

ಕೂದಲು ಸಲೂನ್ ಅಥವಾ ದುರಸ್ತಿ ಅಂಗಡಿಯಲ್ಲಿ ಗ್ರಾಹಕ ಸೇವೆ;

ಉದ್ಯಮಗಳ ಗುಂಪಿಗೆ ಸರಬರಾಜು ಯೋಜನೆಯ ಅನುಷ್ಠಾನ, ಇತ್ಯಾದಿ.

ಈ ಪ್ರತಿಯೊಂದು ಪ್ರಕ್ರಿಯೆಗಳ ನಿರ್ದಿಷ್ಟ ಕೋರ್ಸ್ ಹಲವಾರು ಯಾದೃಚ್ಛಿಕ, ಹಿಂದೆ ಊಹಿಸಲಾಗದ ಅಂಶಗಳ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿದೆ, ಉದಾಹರಣೆಗೆ:

ಷೇರು ಮಾರುಕಟ್ಟೆಯಲ್ಲಿ ರಾಜಕೀಯ ಬದಲಾವಣೆಗಳ ಬಗ್ಗೆ ಅನಿರೀಕ್ಷಿತ ಸುದ್ದಿಗಳ ಆಗಮನ;

ಕ್ಲೈಂಟ್‌ಗಳಿಂದ ಬರುವ ಅಪ್ಲಿಕೇಶನ್‌ಗಳ ಹರಿವಿನ ಯಾದೃಚ್ಛಿಕ ಸ್ವಭಾವ (ಅವಶ್ಯಕತೆಗಳು);

ಪೂರೈಕೆ ಯೋಜನೆಯ ಅನುಷ್ಠಾನದಲ್ಲಿ ಯಾದೃಚ್ಛಿಕ ಅಡಚಣೆಗಳು, ಇತ್ಯಾದಿ.

ವ್ಯಾಖ್ಯಾನ. ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಸಂಭವಿಸುವ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಮಾರ್ಕೋವಿಯನ್(ಅಥವಾ ಪರಿಣಾಮಗಳಿಲ್ಲದೆ ಪ್ರಕ್ರಿಯೆ), ಇದು ಈ ಕೆಳಗಿನ ಆಸ್ತಿಯನ್ನು ಹೊಂದಿದ್ದರೆ: ಪ್ರತಿ ಕ್ಷಣಕ್ಕೂ ಟಿ 0 ಭವಿಷ್ಯದಲ್ಲಿ ವ್ಯವಸ್ಥೆಯ ಯಾವುದೇ ಸ್ಥಿತಿಯ ಸಂಭವನೀಯತೆ (ಜೊತೆ t > t 0)ವರ್ತಮಾನದಲ್ಲಿ ಅದರ ಸ್ಥಿತಿಯನ್ನು ಮಾತ್ರ ಅವಲಂಬಿಸಿರುತ್ತದೆ (ಜೊತೆ t = t 0)ಮತ್ತು ವ್ಯವಸ್ಥೆಯು ಈ ಸ್ಥಿತಿಗೆ ಯಾವಾಗ ಮತ್ತು ಹೇಗೆ ಬಂದಿತು ಎಂಬುದರ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುವುದಿಲ್ಲ (ಅಂದರೆ, ಹಿಂದೆ ಪ್ರಕ್ರಿಯೆಯು ಹೇಗೆ ಅಭಿವೃದ್ಧಿಗೊಂಡಿತು).

ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ, ಅದರ ಭವಿಷ್ಯದ ಅಭಿವೃದ್ಧಿಯು ಪ್ರಸ್ತುತ ಸ್ಥಿತಿಯನ್ನು ಮಾತ್ರ ಅವಲಂಬಿಸಿರುತ್ತದೆ ಮತ್ತು ಪ್ರಕ್ರಿಯೆಯ "ಪೂರ್ವ ಇತಿಹಾಸ" ವನ್ನು ಅವಲಂಬಿಸಿರುವುದಿಲ್ಲ.

ಒಂದು ಉದಾಹರಣೆಯನ್ನು ನೋಡೋಣ. ವ್ಯವಸ್ಥೆ ಬಿಡಿ ಎಸ್ಸ್ವಲ್ಪ ಸಮಯದವರೆಗೆ ಇರುವ ಷೇರು ಮಾರುಕಟ್ಟೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ. ಭವಿಷ್ಯದಲ್ಲಿ ವ್ಯವಸ್ಥೆಯು ಹೇಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ ಎಂಬುದರ ಕುರಿತು ನಾವು ಆಸಕ್ತಿ ಹೊಂದಿದ್ದೇವೆ. ಭವಿಷ್ಯದ ಕಾರ್ಯಕ್ಷಮತೆಯ ಗುಣಲಕ್ಷಣಗಳು (ಒಂದು ವಾರದಲ್ಲಿ ನಿರ್ದಿಷ್ಟ ಸ್ಟಾಕ್‌ನ ಬೆಲೆಯಲ್ಲಿ ಕುಸಿತದ ಸಂಭವನೀಯತೆಗಳು) ಈ ಕ್ಷಣದಲ್ಲಿ ಸಿಸ್ಟಮ್ ಸ್ಥಿತಿಯನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ (ವಿವಿಧ ಅಂಶಗಳು) ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ. ಸರ್ಕಾರದ ನಿರ್ಧಾರಗಳು ಅಥವಾ ಚುನಾವಣಾ ಫಲಿತಾಂಶಗಳು ಇಲ್ಲಿ ಮಧ್ಯಪ್ರವೇಶಿಸಬಹುದಾದ್ದರಿಂದ) ಮತ್ತು ವ್ಯವಸ್ಥೆಯು ತನ್ನ ಪ್ರಸ್ತುತ ಸ್ಥಿತಿಯನ್ನು ಯಾವಾಗ ಮತ್ತು ಹೇಗೆ ತಲುಪಿತು ಎಂಬುದರ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿಲ್ಲ (ಹಿಂದೆ ಈ ಷೇರುಗಳ ಬೆಲೆ ಚಲನೆಯ ಸ್ವರೂಪವನ್ನು ಅವಲಂಬಿಸಿಲ್ಲ).

ಪ್ರಾಯೋಗಿಕವಾಗಿ, ನಾವು ಸಾಮಾನ್ಯವಾಗಿ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ಎದುರಿಸುತ್ತೇವೆ, ಅದು ವಿಭಿನ್ನ ಹಂತದ ಅಂದಾಜುಗಳನ್ನು ಮಾರ್ಕೋವಿಯನ್ ಎಂದು ಪರಿಗಣಿಸಬಹುದು.

ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳ ಸಿದ್ಧಾಂತವು ವ್ಯಾಪಕವಾದ ವಿವಿಧ ಅನ್ವಯಿಕೆಗಳನ್ನು ಹೊಂದಿದೆ. ಕಾರ್ಯಾಚರಣೆಗಳ ಗಣಿತದ ಮಾದರಿಗಳ ನಿರ್ಮಾಣಕ್ಕೆ ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳ ಸಿದ್ಧಾಂತದ ಅನ್ವಯದಲ್ಲಿ ನಾವು ಮುಖ್ಯವಾಗಿ ಆಸಕ್ತಿ ಹೊಂದಿದ್ದೇವೆ, ಅದರ ಕೋರ್ಸ್ ಮತ್ತು ಫಲಿತಾಂಶವು ಯಾದೃಚ್ಛಿಕ ಅಂಶಗಳ ಮೇಲೆ ಗಮನಾರ್ಹವಾಗಿ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ.

ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ವಿಂಗಡಿಸಲಾಗಿದೆ ತರಗತಿಗಳು"ಎಸ್" ವ್ಯವಸ್ಥೆಯು ಹೇಗೆ ಮತ್ತು ಯಾವ ಸಮಯದಲ್ಲಿ ಅದರ ಸ್ಥಿತಿಯನ್ನು ಬದಲಾಯಿಸಬಹುದು ಎಂಬುದರ ಆಧಾರದ ಮೇಲೆ.

ವ್ಯಾಖ್ಯಾನ. ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಪ್ರತ್ಯೇಕ ರಾಜ್ಯಗಳೊಂದಿಗೆ ಪ್ರಕ್ರಿಯೆ,ಸಾಧ್ಯವಾದರೆ ವ್ಯವಸ್ಥೆಯ ಸ್ಥಿತಿಗಳು s x, s 2, s v... ಪಟ್ಟಿ ಮಾಡಬಹುದು (ಸಂಖ್ಯೆಯ) ಒಂದರ ನಂತರ ಒಂದರಂತೆ, ಮತ್ತು ಪ್ರಕ್ರಿಯೆಯು ಕಾಲಕಾಲಕ್ಕೆ ಸಿಸ್ಟಮ್ ಆಗಿದೆ ಎಸ್ಒಂದು ರಾಜ್ಯದಿಂದ ಇನ್ನೊಂದಕ್ಕೆ ಥಟ್ಟನೆ (ತಕ್ಷಣ) ಜಿಗಿಯುತ್ತದೆ.

ಉದಾಹರಣೆಗೆ, ಯೋಜನೆಯ ಅಭಿವೃದ್ಧಿ ಎಸ್ಎರಡು ಇಲಾಖೆಗಳು ಜಂಟಿಯಾಗಿ ನಡೆಸುತ್ತವೆ, ಪ್ರತಿಯೊಂದೂ ತಪ್ಪು ಮಾಡಬಹುದು. ಕೆಳಗಿನ ಸಿಸ್ಟಮ್ ಸ್ಥಿತಿಗಳು ಸಾಧ್ಯ:

5, - ಎರಡೂ ಇಲಾಖೆಗಳು ಸಾಮಾನ್ಯವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿವೆ;

ರು 2 - ಮೊದಲ ಇಲಾಖೆ ತಪ್ಪು ಮಾಡಿದೆ, ಎರಡನೆಯದು ಉತ್ತಮವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿದೆ;

ರು 3 - ಎರಡನೇ ಇಲಾಖೆ ತಪ್ಪು ಮಾಡಿದೆ, ಮೊದಲನೆಯದು ಉತ್ತಮವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿದೆ;

ರು 4 - ಎರಡೂ ಇಲಾಖೆಗಳು ತಪ್ಪು ಮಾಡಿದೆ.

ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ನಡೆಯುತ್ತಿರುವ ಪ್ರಕ್ರಿಯೆಯು ಯಾದೃಚ್ಛಿಕವಾಗಿ ಕೆಲವು ಹಂತಗಳಲ್ಲಿ ರಾಜ್ಯದಿಂದ ರಾಜ್ಯಕ್ಕೆ ಚಲಿಸುತ್ತದೆ ("ಜಿಗಿತಗಳು"). ವ್ಯವಸ್ಥೆಯು ಒಟ್ಟು ನಾಲ್ಕು ಸಂಭವನೀಯ ರಾಜ್ಯಗಳನ್ನು ಹೊಂದಿದೆ. ನಮ್ಮ ಮುಂದೆ ಪ್ರತ್ಯೇಕ ರಾಜ್ಯಗಳೊಂದಿಗೆ ಪ್ರಕ್ರಿಯೆ ಇದೆ.

ಪ್ರತ್ಯೇಕ ರಾಜ್ಯಗಳೊಂದಿಗೆ ಪ್ರಕ್ರಿಯೆಗಳ ಜೊತೆಗೆ, ಇವೆ ನಿರಂತರ ಸ್ಥಿತಿಗಳೊಂದಿಗೆ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳು: ಈ ಪ್ರಕ್ರಿಯೆಗಳು ರಾಜ್ಯದಿಂದ ರಾಜ್ಯಕ್ಕೆ ಕ್ರಮೇಣ, ಸುಗಮ ಪರಿವರ್ತನೆಯಿಂದ ನಿರೂಪಿಸಲ್ಪಡುತ್ತವೆ. ಉದಾಹರಣೆಗೆ, ಬೆಳಕಿನ ನೆಟ್ವರ್ಕ್ನಲ್ಲಿ ವೋಲ್ಟೇಜ್ ಅನ್ನು ಬದಲಾಯಿಸುವ ಪ್ರಕ್ರಿಯೆಯು ನಿರಂತರ ಸ್ಥಿತಿಗಳೊಂದಿಗೆ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯಾಗಿದೆ.

ನಾವು ಪ್ರತ್ಯೇಕ ರಾಜ್ಯಗಳೊಂದಿಗೆ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ಮಾತ್ರ ಪರಿಗಣಿಸುತ್ತೇವೆ.

ಪ್ರತ್ಯೇಕ ರಾಜ್ಯಗಳೊಂದಿಗೆ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ವಿಶ್ಲೇಷಿಸುವಾಗ, ಜ್ಯಾಮಿತೀಯ ಯೋಜನೆಯನ್ನು ಬಳಸಲು ಇದು ತುಂಬಾ ಅನುಕೂಲಕರವಾಗಿದೆ - ರಾಜ್ಯ ಗ್ರಾಫ್ ಎಂದು ಕರೆಯಲ್ಪಡುವ. ರಾಜ್ಯದ ಗ್ರಾಫ್ಜ್ಯಾಮಿತೀಯವಾಗಿ ವ್ಯವಸ್ಥೆಯ ಸಂಭವನೀಯ ಸ್ಥಿತಿಗಳನ್ನು ಮತ್ತು ರಾಜ್ಯದಿಂದ ರಾಜ್ಯಕ್ಕೆ ಅದರ ಸಂಭವನೀಯ ಪರಿವರ್ತನೆಗಳನ್ನು ಚಿತ್ರಿಸುತ್ತದೆ.

ವ್ಯವಸ್ಥೆ ಇರಲಿ ಎಸ್ಪ್ರತ್ಯೇಕ ರಾಜ್ಯಗಳೊಂದಿಗೆ:

ಪ್ರತಿಯೊಂದು ರಾಜ್ಯವನ್ನು ಒಂದು ಆಯತದಿಂದ ಪ್ರತಿನಿಧಿಸಲಾಗುತ್ತದೆ ಮತ್ತು ರಾಜ್ಯದಿಂದ ರಾಜ್ಯಕ್ಕೆ ಸಂಭವನೀಯ ಪರಿವರ್ತನೆಗಳು ("ಜಂಪ್‌ಗಳು") ಈ ಆಯತಗಳನ್ನು ಸಂಪರ್ಕಿಸುವ ಬಾಣಗಳಿಂದ ಪ್ರತಿನಿಧಿಸಲಾಗುತ್ತದೆ. ರಾಜ್ಯದ ಗ್ರಾಫ್ನ ಉದಾಹರಣೆಯನ್ನು ಅಂಜೂರದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. 4.1.

ಬಾಣಗಳು ರಾಜ್ಯದಿಂದ ರಾಜ್ಯಕ್ಕೆ ನೇರ ಪರಿವರ್ತನೆಗಳನ್ನು ಮಾತ್ರ ಗುರುತಿಸುತ್ತವೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ; ವ್ಯವಸ್ಥೆಯು ರಾಜ್ಯದಿಂದ ಪರಿವರ್ತನೆ ಸಾಧ್ಯವಾದರೆ ರು 2 5 3 ನಲ್ಲಿ ಮಾತ್ರ ಮೂಲಕ ಎಸ್ ವೈನಂತರ ಬಾಣಗಳು ಪರಿವರ್ತನೆಗಳನ್ನು ಮಾತ್ರ ಗುರುತಿಸುತ್ತವೆ ರು 2-> ಮತ್ತು ಎಲ್, 1 -> 5 3, ಆದರೆ ಅಲ್ಲ ರು 2 -» ಎಸ್ ವೈಕೆಲವು ಉದಾಹರಣೆಗಳನ್ನು ನೋಡೋಣ:

1. ವ್ಯವಸ್ಥೆ ಎಸ್- ಐದು ಸಂಭವನೀಯ ರಾಜ್ಯಗಳಲ್ಲಿ ಒಂದಾಗಬಹುದಾದ ಕಂಪನಿ: ರು]- ಲಾಭದೊಂದಿಗೆ ಕೆಲಸ ಮಾಡುತ್ತದೆ;

ರು 2- ಅದರ ಅಭಿವೃದ್ಧಿ ನಿರೀಕ್ಷೆಗಳನ್ನು ಕಳೆದುಕೊಂಡಿತು ಮತ್ತು ಲಾಭವನ್ನು ಗಳಿಸುವುದನ್ನು ನಿಲ್ಲಿಸಿತು;

5 3 - ಸಂಭಾವ್ಯ ಸ್ವಾಧೀನಕ್ಕೆ ವಸ್ತುವಾಯಿತು;

s 4- ಬಾಹ್ಯ ನಿಯಂತ್ರಣದಲ್ಲಿದೆ;

ರು 5- ದಿವಾಳಿಯಾದ ಕಂಪನಿಯ ಆಸ್ತಿಯನ್ನು ಹರಾಜಿನಲ್ಲಿ ಮಾರಾಟ ಮಾಡಲಾಗುತ್ತದೆ.

ಕಂಪನಿಯ ರಾಜ್ಯ ಗ್ರಾಫ್ ಅನ್ನು ಅಂಜೂರದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. 4.2.

ಅಕ್ಕಿ. 4.2

• 2. ವ್ಯವಸ್ಥೆ ಎಸ್- ಎರಡು ಶಾಖೆಗಳನ್ನು ಹೊಂದಿರುವ ಬ್ಯಾಂಕ್. ಕೆಳಗಿನ ಸಿಸ್ಟಮ್ ಸ್ಥಿತಿಗಳು ಸಾಧ್ಯ:
• 5, - ಎರಡೂ ಶಾಖೆಗಳು ಲಾಭದಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತವೆ;

ರು 2 - ಮೊದಲ ಶಾಖೆ ಲಾಭವಿಲ್ಲದೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ, ಎರಡನೆಯದು ಲಾಭದೊಂದಿಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ;

5 3 - ಎರಡನೇ ಶಾಖೆಯು ಲಾಭವಿಲ್ಲದೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ, ಮೊದಲನೆಯದು ಲಾಭದೊಂದಿಗೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತದೆ;

ರು 4 - ಎರಡೂ ಶಾಖೆಗಳು ಲಾಭವಿಲ್ಲದೆ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತವೆ.

ಪರಿಸ್ಥಿತಿಯಲ್ಲಿ ಯಾವುದೇ ಸುಧಾರಣೆ ಇಲ್ಲ ಎಂದು ಭಾವಿಸಲಾಗಿದೆ.

ರಾಜ್ಯದ ಗ್ರಾಫ್ ಅನ್ನು ಅಂಜೂರದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. 4.3. ಗ್ರಾಫ್ ರಾಜ್ಯದಿಂದ ಸಂಭವನೀಯ ಪರಿವರ್ತನೆಯನ್ನು ತೋರಿಸುವುದಿಲ್ಲ ಎಂಬುದನ್ನು ಗಮನಿಸಿ ರು]ನೇರವಾಗಿ ಗೆ s4,ಬ್ಯಾಂಕ್ ವೇಳೆ ನಿಜವಾಗುತ್ತದೆ ನೇರವಾಗಿನಷ್ಟದಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸಲಿದೆ. ಅಭ್ಯಾಸವು ದೃಢೀಕರಿಸಿದಂತೆ ಅಂತಹ ಘಟನೆಯ ಸಾಧ್ಯತೆಯನ್ನು ನಿರ್ಲಕ್ಷಿಸಬಹುದು.

ಅಕ್ಕಿ. 4.3

3. ವ್ಯವಸ್ಥೆ ಎಸ್- ಎರಡು ವ್ಯಾಪಾರಿಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ಹೂಡಿಕೆ ಕಂಪನಿ (ಇಲಾಖೆಗಳು): I ಮತ್ತು II; ಅವುಗಳಲ್ಲಿ ಪ್ರತಿಯೊಂದೂ ಕೆಲವು ಸಮಯದಲ್ಲಿ ನಷ್ಟದಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸಲು ಪ್ರಾರಂಭಿಸಬಹುದು. ಇದು ಸಂಭವಿಸಿದಲ್ಲಿ, ಕಂಪನಿಯ ನಿರ್ವಹಣೆ ತಕ್ಷಣವೇ ಇಲಾಖೆಯ ಲಾಭದಾಯಕ ಕಾರ್ಯಾಚರಣೆಯನ್ನು ಪುನಃಸ್ಥಾಪಿಸಲು ಕ್ರಮಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ.

ಸಂಭಾವ್ಯ ವ್ಯವಸ್ಥೆಯು ಹೇಳುತ್ತದೆ: ರು- ಎರಡೂ ಇಲಾಖೆಗಳ ಚಟುವಟಿಕೆಗಳು ಲಾಭದಾಯಕವಾಗಿವೆ; ರು 2- ಮೊದಲ ವಿಭಾಗವನ್ನು ಪುನಃಸ್ಥಾಪಿಸಲಾಗುತ್ತಿದೆ, ಎರಡನೆಯದು ಲಾಭದಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿದೆ;

s 3- ಮೊದಲ ವಿಭಾಗವು ಲಾಭದಲ್ಲಿ ಕಾರ್ಯನಿರ್ವಹಿಸುತ್ತಿದೆ, ಎರಡನೆಯದನ್ನು ಪುನಃಸ್ಥಾಪಿಸಲಾಗುತ್ತಿದೆ;

s 4- ಎರಡೂ ಇಲಾಖೆಗಳನ್ನು ಪುನಃಸ್ಥಾಪಿಸಲಾಗುತ್ತಿದೆ.

ಸಿಸ್ಟಮ್ ಸ್ಟೇಟ್ ಗ್ರಾಫ್ ಅನ್ನು ಅಂಜೂರದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. 4.4

4. ಹಿಂದಿನ ಉದಾಹರಣೆಯ ಪರಿಸ್ಥಿತಿಗಳಲ್ಲಿ, ಪ್ರತಿ ವ್ಯಾಪಾರಿಯ ಚಟುವಟಿಕೆಗಳು, ಅವರು ಇಲಾಖೆಯ ಲಾಭದಾಯಕ ಕೆಲಸವನ್ನು ಪುನಃಸ್ಥಾಪಿಸಲು ಪ್ರಾರಂಭಿಸುವ ಮೊದಲು, ಅದನ್ನು ಸುಧಾರಿಸಲು ಕ್ರಮಗಳನ್ನು ತೆಗೆದುಕೊಳ್ಳಲು ಕಂಪನಿಯ ನಿರ್ವಹಣೆಯಿಂದ ಅಧ್ಯಯನಕ್ಕೆ ಒಳಪಟ್ಟಿರುತ್ತದೆ.

ಅನುಕೂಲಕ್ಕಾಗಿ, ನಾವು ಸಿಸ್ಟಮ್ನ ರಾಜ್ಯಗಳನ್ನು ಒಂದಲ್ಲ, ಆದರೆ ಎರಡು ಸೂಚ್ಯಂಕಗಳೊಂದಿಗೆ ಸಂಖ್ಯೆ ಮಾಡುತ್ತೇವೆ; ಮೊದಲನೆಯದು ಮೊದಲ ವ್ಯಾಪಾರಿಯ ಸ್ಥಿತಿಯನ್ನು ಅರ್ಥೈಸುತ್ತದೆ (1 - ಲಾಭದೊಂದಿಗೆ ಕೆಲಸ ಮಾಡುತ್ತದೆ, 2 - ಅವನ ಚಟುವಟಿಕೆಗಳನ್ನು ನಿರ್ವಹಣೆಯಿಂದ ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತಿದೆ, 3 - ಇಲಾಖೆಯ ಲಾಭದಾಯಕ ಚಟುವಟಿಕೆಯನ್ನು ಪುನಃಸ್ಥಾಪಿಸುತ್ತದೆ); ಎರಡನೆಯದು - ಎರಡನೇ ವ್ಯಾಪಾರಿಗೆ ಅದೇ ರಾಜ್ಯಗಳು. ಉದಾಹರಣೆಗೆ, ರು 23ಇದರರ್ಥ: ಮೊದಲ ವ್ಯಾಪಾರಿಯ ಚಟುವಟಿಕೆಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತಿದೆ, ಎರಡನೆಯದು ಲಾಭದಾಯಕ ಕೆಲಸವನ್ನು ಮರುಸ್ಥಾಪಿಸುತ್ತಿದೆ.

ಸಂಭಾವ್ಯ ಸಿಸ್ಟಮ್ ರಾಜ್ಯಗಳು ಎಸ್:

ಎಸ್ ಯು- ಎರಡೂ ವ್ಯಾಪಾರಿಗಳ ಚಟುವಟಿಕೆಗಳು ಲಾಭವನ್ನು ತರುತ್ತವೆ;

s l2- ಮೊದಲ ವ್ಯಾಪಾರಿ ಲಾಭದೊಂದಿಗೆ ಕೆಲಸ ಮಾಡುತ್ತಾನೆ, ಎರಡನೆಯ ಚಟುವಟಿಕೆಗಳನ್ನು ಕಂಪನಿಯ ನಿರ್ವಹಣೆಯಿಂದ ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತದೆ;

5 13 - ಮೊದಲ ವ್ಯಾಪಾರಿ ಲಾಭದೊಂದಿಗೆ ಕೆಲಸ ಮಾಡುತ್ತಾನೆ, ಎರಡನೆಯದು ಇಲಾಖೆಯ ಲಾಭದಾಯಕ ಚಟುವಟಿಕೆಯನ್ನು ಪುನಃಸ್ಥಾಪಿಸುತ್ತದೆ;

ರು 2ಲೀ- ಮೊದಲ ವ್ಯಾಪಾರಿಯ ಚಟುವಟಿಕೆಗಳನ್ನು ನಿರ್ವಹಣೆಯಿಂದ ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತದೆ, ಎರಡನೆಯದು ಲಾಭದೊಂದಿಗೆ ಕೆಲಸ ಮಾಡುತ್ತದೆ;

ರು 22 - ಎರಡೂ ವ್ಯಾಪಾರಿಗಳ ಚಟುವಟಿಕೆಗಳನ್ನು ನಿರ್ವಹಣೆಯಿಂದ ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತದೆ;

• 5 23 - ಮೊದಲ ವ್ಯಾಪಾರಿಯ ಕೆಲಸವನ್ನು ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತದೆ, ಎರಡನೇ ವ್ಯಾಪಾರಿ ಇಲಾಖೆಯ ಲಾಭದಾಯಕ ಚಟುವಟಿಕೆಗಳನ್ನು ಪುನಃಸ್ಥಾಪಿಸುತ್ತಾನೆ;
• 5 31 - ಮೊದಲ ವ್ಯಾಪಾರಿ ಇಲಾಖೆಯ ಲಾಭದಾಯಕ ಚಟುವಟಿಕೆಗಳನ್ನು ಪುನಃಸ್ಥಾಪಿಸುತ್ತಾನೆ, ಎರಡನೆಯದು ಲಾಭದೊಂದಿಗೆ ಕೆಲಸ ಮಾಡುತ್ತದೆ;
• 5 32 - ಇಲಾಖೆಯ ಲಾಭದಾಯಕ ಚಟುವಟಿಕೆಯನ್ನು ಮೊದಲ ವ್ಯಾಪಾರಿಯಿಂದ ಪುನಃಸ್ಥಾಪಿಸಲಾಗುತ್ತದೆ, ಎರಡನೇ ವ್ಯಾಪಾರಿಯ ಕೆಲಸವನ್ನು ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತದೆ;
• 5 33 - ಇಬ್ಬರೂ ವ್ಯಾಪಾರಿಗಳು ತಮ್ಮ ಇಲಾಖೆಯ ಲಾಭದಾಯಕ ಕೆಲಸವನ್ನು ಪುನಃಸ್ಥಾಪಿಸುತ್ತಾರೆ.

ಒಟ್ಟು ಒಂಬತ್ತು ರಾಜ್ಯಗಳಿವೆ. ರಾಜ್ಯದ ಗ್ರಾಫ್ ಅನ್ನು ಅಂಜೂರದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. 4.5

ವಿಭಾಗ 5.1.6 ರಲ್ಲಿ ನೀಡಲಾದ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ವ್ಯಾಖ್ಯಾನದಿಂದ, ಹಾಗೆಯೇ ನೇರವಾಗಿ ಸೂತ್ರದಿಂದ (5.6), ಇದು ಅನುಸರಿಸುತ್ತದೆ

ಷರತ್ತುಬದ್ಧ ಸಾಂದ್ರತೆ

ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಸ್ಥಿತ್ಯಂತರದ ಸಂಭವನೀಯತೆ ಸಾಂದ್ರತೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ y ಸಮಯದಲ್ಲಿ s ನಿಂದ x ಸಮಯದಲ್ಲಿ t ಗೆ.

ಸೂತ್ರವನ್ನು ಬಳಸಿ (2.57), ನಾವು ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಬಹುಆಯಾಮದ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯನ್ನು (ಯಾವುದೇ ಸೀಮಿತ ಕ್ರಮದ) ನಿರ್ಧರಿಸುತ್ತೇವೆ

ಫಾರ್ಮುಲಾ (5.60) ಎಂದರೆ ಮಾರ್ಕೋವ್ ಪ್ರಕ್ರಿಯೆಯ ಬಹುಆಯಾಮದ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯ ಅಪವರ್ತನೀಕರಣ - ಒಂದು ಆಯಾಮದ ಸಾಂದ್ರತೆ ಮತ್ತು ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯ ಉತ್ಪನ್ನವಾಗಿ ಅದರ ಪ್ರಾತಿನಿಧ್ಯ. ಬಹುಆಯಾಮದ ಸಾಂದ್ರತೆಯ ಅಪವರ್ತನ ಸ್ಥಿತಿ (5.60) ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಳ ವಿಶಿಷ್ಟ ಲಕ್ಷಣವಾಗಿದೆ (ಸ್ವತಂತ್ರ ಮೌಲ್ಯಗಳೊಂದಿಗೆ ಪ್ರಕ್ರಿಯೆಗಳಿಗೆ ಇದೇ ರೀತಿಯ ಸರಳವಾದ ಅಪವರ್ತನೀಕರಣ ಸ್ಥಿತಿಯೊಂದಿಗೆ (5.4) ಹೋಲಿಕೆ ಮಾಡಿ).

ಏಕ-ಆಯಾಮದ ಸಾಂದ್ರತೆ ಮತ್ತು ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯು ಸಂಬಂಧದಿಂದ ಸಂಬಂಧಿಸಿದೆ

ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯು ಅನಿಯಂತ್ರಿತ ಷರತ್ತುಬದ್ಧ ವಿತರಣಾ ಕಾರ್ಯವಲ್ಲ, ಅದು ಋಣಾತ್ಮಕವಲ್ಲದ ಮತ್ತು ಸಾಮಾನ್ಯೀಕರಣದ ಸಾಮಾನ್ಯ ಪರಿಸ್ಥಿತಿಗಳನ್ನು ಮಾತ್ರ ಪೂರೈಸುತ್ತದೆ, ಅಂದರೆ. ಇದು ಕೆಲವು ಸಮಗ್ರ ಸಮೀಕರಣವನ್ನು ಸಹ ಪೂರೈಸಬೇಕು. ವಾಸ್ತವವಾಗಿ, (5.60) ನಿಂದ ನಾವು ಹೊಂದಿದ್ದೇವೆ

ಈ ಸಮಾನತೆಯ ಎರಡೂ ಬದಿಗಳನ್ನು ಒಟ್ಟುಗೂಡಿಸಿ, ನಾವು ಪಡೆಯುತ್ತೇವೆ

ಮತ್ತು ಅಂದಿನಿಂದ

ಸಮಗ್ರ ಸಮೀಕರಣವನ್ನು (5.62) ಕೊಲ್ಮೊಗೊರೊವ್-ಚಾಪ್ಮನ್ ಸಮೀಕರಣ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

5.4.2. ಏಕರೂಪದ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಳು.

ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯು ಸಮಯ ಬದಲಾವಣೆಗೆ ಬದಲಾಗದಿದ್ದರೆ, ಅದನ್ನು ಏಕರೂಪದ (ಸ್ಥಾಯಿ) ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆ ಸಾಂದ್ರತೆ (5.59) ಕೇವಲ ಒಂದು ಬಾರಿ ನಿಯತಾಂಕವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.

ಏಕರೂಪದ ಮಾರ್ಕೋವ್ ಪ್ರಕ್ರಿಯೆಯ ಬಹುಆಯಾಮದ ಸಾಂದ್ರತೆಯ ಅಪವರ್ತನ ಸ್ಥಿತಿಯನ್ನು ರೂಪದಲ್ಲಿ ಬರೆಯಲಾಗಿದೆ) [ನೋಡಿ (5.60)]

ಏಕರೂಪದ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಳ ವರ್ಗವು ಸ್ವತಂತ್ರ ಏರಿಕೆಗಳೊಂದಿಗೆ ಏಕರೂಪದ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳ ಪರಿಗಣಿಸಲಾದ ವರ್ಗದೊಂದಿಗೆ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ.

5.4.3. ಸಂಪರ್ಕಿತ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಗುಣಿಸಿ.

ನಾವು ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಕರೆಯುತ್ತೇವೆ - ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯು ಪ್ರಕ್ರಿಯೆಯ k ಹಿಂದಿನ ಮೌಲ್ಯಗಳನ್ನು ಅವಲಂಬಿಸಿದ್ದರೆ ಸಂಪರ್ಕಗೊಂಡಿದೆ [ನೋಡಿ (5.58)]:

ಸಂಪರ್ಕಿತ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಬಹುಆಯಾಮದ ಸಾಂದ್ರತೆಯ ಅಪವರ್ತನ ಸ್ಥಿತಿಯನ್ನು ಹೀಗೆ ಬರೆಯಲಾಗಿದೆ

ಮತ್ತು ಕೊಲ್ಮೊಗೊರೊವ್-ಚಾಪ್ಮನ್ ಸಮೀಕರಣ

5.4.4. ವೆಕ್ಟರ್ ಮಾರ್ಕೋವ್ ಪ್ರಕ್ರಿಯೆ.

ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳ ಒಂದು ಸೆಟ್ ವೆಕ್ಟರ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯನ್ನು ರೂಪಿಸುತ್ತದೆ, ಈ ಗುಂಪಿನ ಸಂಪೂರ್ಣ ಸಂಭವನೀಯ ವಿವರಣೆಗಾಗಿ ಜಂಟಿ ವಿತರಣೆಯನ್ನು ತಿಳಿದುಕೊಳ್ಳಲು ಇದು ಅವಶ್ಯಕ ಮತ್ತು ಸಾಕಾಗುತ್ತದೆ.

ಮತ್ತು ಷರತ್ತುಬದ್ಧ ವಿತರಣೆ

ಅಥವಾ ಅನುಗುಣವಾದ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆ

ಬದಲಿಸುವುದು - (5.62) ವೆಕ್ಟರ್ ಪದಗಳಿಗಿಂತ ಸ್ಕೇಲಾರ್ ಪ್ರಮಾಣಗಳು, ನಾವು ವೆಕ್ಟರ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗೆ ಅನುಗುಣವಾದ ಸಂಬಂಧಗಳನ್ನು ಪಡೆಯುತ್ತೇವೆ.

ವೆಕ್ಟರ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯನ್ನು ರೂಪಿಸುವ ಸೆಟ್‌ಗೆ ಸೇರಿದ ಪ್ರತಿಯೊಂದು ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ವೆಕ್ಟರ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಒಂದು ಘಟಕ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಆದಾಗ್ಯೂ, ಸಾಮಾನ್ಯವಾಗಿ ಹೇಳುವುದಾದರೆ, ಸ್ಕೇಲಾರ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯಲ್ಲ.

ವೆಕ್ಟರ್ ಮತ್ತು ಗುಣಿಸಿ ಸಂಪರ್ಕಿತ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಳ ನಡುವಿನ ಸಂಪರ್ಕವನ್ನು ನಾವು ಗಮನಿಸೋಣ: a -ಸಂಪರ್ಕಿತ ಮಾರ್ಕೊವ್ ಅನುಕ್ರಮವನ್ನು ವೆಕ್ಟರ್ (ಗಾತ್ರ k) ಮಾರ್ಕೊವ್ ಅನುಕ್ರಮವಾಗಿಯೂ ಅರ್ಥೈಸಿಕೊಳ್ಳಬಹುದು

5.4.5. ಗಾಸಿಯನ್ ಮಾರ್ಕೋವ್ ಪ್ರಕ್ರಿಯೆ.

ಅದರ ವಿತರಣೆಯು ಸಾಮಾನ್ಯ ಸಂಭವನೀಯತೆಯ ವಿತರಣಾ ಕಾನೂನನ್ನು ಪಾಲಿಸಿದರೆ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಗಾಸಿಯನ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ (ವಿಭಾಗ 5.2.1 ನೋಡಿ). ಯಾವುದೇ ಗಾಸಿಯನ್ ಪ್ರಕ್ರಿಯೆಗೆ ಸಂಬಂಧಿಸಿದಂತೆ, ಗಾಸಿಯನ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಪರಸ್ಪರ ಸಂಬಂಧದ ಕಾರ್ಯವು ಅದರ ಸಂಪೂರ್ಣ ಸಂಭವನೀಯ ವಿವರಣೆಯನ್ನು ಒದಗಿಸುತ್ತದೆ. ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯು ಕೇಂದ್ರೀಕೃತ ಗಾಸಿಯನ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆ ಎಂದು ಸಾಬೀತುಪಡಿಸಬಹುದು ಮತ್ತು ಅದರ ಪರಸ್ಪರ ಕ್ರಿಯೆಯಲ್ಲಿ ಸಮೀಕರಣವನ್ನು ಪೂರೈಸಿದರೆ ಮಾತ್ರ

ಏಕರೂಪದ ಗಾಸ್ಸಿಯನ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಾಗಿ, ಸ್ಥಿತಿಯನ್ನು (5.71) ಸಾಮಾನ್ಯೀಕರಿಸಿದ ಪರಸ್ಪರ ಕ್ರಿಯೆಯನ್ನು ಬಳಸಿಕೊಂಡು ಬರೆಯಲಾಗುತ್ತದೆ, ಇದು ಸ್ವಾಭಾವಿಕವಾಗಿ ಒಂದು ವಾದವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ.

ಕ್ಷುಲ್ಲಕ ಪರಿಹಾರವನ್ನು ಹೊರತುಪಡಿಸಿ, ಸಮೀಕರಣವು (5.72) ವಿಶಿಷ್ಟ ಪರಿಹಾರವನ್ನು ಹೊಂದಿದೆ

ಹೀಗಾಗಿ, ಪ್ರಸರಣದೊಂದಿಗೆ ಸ್ಥಾಯಿ ಕೇಂದ್ರಿತ ಗಾಸ್ಸಿಯನ್ ಪ್ರಕ್ರಿಯೆಯು ಮಾರ್ಕೋವಿಯನ್ ಆಗಿದ್ದರೆ ಮತ್ತು ಅದರ ಪರಸ್ಪರ ಸಂಬಂಧ ಕಾರ್ಯ (ಚಿತ್ರ 5.4)

ಅಥವಾ ಅನುಗುಣವಾದ ಪ್ರಕ್ರಿಯೆಯ ಶಕ್ತಿ ರೋಹಿತದ ಸಾಂದ್ರತೆ (Fig. 5.5)

(5.74) ರಿಂದ ಮತ್ತು, ಅದರ ಪ್ರಕಾರ, (5.75) ನಿಂದ, ಸರಾಸರಿ ಚೌಕದಲ್ಲಿ ಏಕರೂಪದ ಗಾಸಿಯನ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯು ನಿರಂತರವಾಗಿರುತ್ತದೆ ಎಂದು ಅನುಸರಿಸುತ್ತದೆ, ಆದರೆ ಸಮಸ್ಯೆ 5.6 ಸಹ ಸರಾಸರಿ ಚೌಕದಲ್ಲಿ ಭಿನ್ನವಾಗಿರುವುದಿಲ್ಲ.

ಅಕ್ಕಿ. 5.4 ಏಕರೂಪದ ಗಾಸಿಯನ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಸಾಮಾನ್ಯೀಕೃತ ಪರಸ್ಪರ ಸಂಬಂಧ ಕಾರ್ಯ

ಅಕ್ಕಿ. 5.5 ಏಕರೂಪದ ಗಾಸಿಯನ್ ಮಾರ್ಕೋವ್ ಪ್ರಕ್ರಿಯೆಯ ಶಕ್ತಿಯ ರೋಹಿತದ ಸಾಂದ್ರತೆ

5.4.6. ಗಾಸಿಯನ್ ಮಾರ್ಕೋವ್ ಅನುಕ್ರಮ.

ವ್ಯತ್ಯಾಸಗಳು ಮತ್ತು ಪರಸ್ಪರ ಸಂಬಂಧದ ಗುಣಾಂಕಗಳೊಂದಿಗೆ ಕೇಂದ್ರೀಕೃತ ಗಾಸಿಯನ್ ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಅನುಕ್ರಮವಾಗಿರಲಿ. ಈ ಅನುಕ್ರಮವು ಮಾರ್ಕೋವಿಯನ್ ಆಗಲು, ಇದು ಅಗತ್ಯ ಮತ್ತು ಸಾಕಷ್ಟು

ಸ್ಥಾಯಿ ಗಾಸಿಯನ್ ಮಾರ್ಕೊವ್ ಅನುಕ್ರಮಕ್ಕಾಗಿ, (5.76) ರಿಂದ ಇದು ಅನುಸರಿಸುತ್ತದೆ

ಅನುಕ್ರಮದ ಎರಡು ಪಕ್ಕದ ಸದಸ್ಯರ ನಡುವಿನ ಪರಸ್ಪರ ಸಂಬಂಧದ ಗುಣಾಂಕ ಎಲ್ಲಿದೆ.

ಗಾಸಿಯನ್ ಮಾರ್ಕೋವ್ ಅನುಕ್ರಮದ ಪ್ರತಿಯೊಂದು ಅನುಕ್ರಮವೂ ಸಹ ಗಾಸಿಯನ್, ಮಾರ್ಕೋವಿಯನ್ ಆಗಿದೆ.

5.4.7. ನಿರಂತರ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಗೆ ಡಿಫರೆನ್ಷಿಯಲ್ ಸಮೀಕರಣ.

ಕೊಲ್ಮೊಗೊರೊವ್-ಚಾಪ್ಮನ್ ಸಮಗ್ರ ಸಮೀಕರಣವನ್ನು (5.62) ಪರಿಹರಿಸುವುದು ಕಷ್ಟದ ಕೆಲಸ. ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯನ್ನು ನಿರ್ಧರಿಸುವುದು ನಾವು ನಿರಂತರ ಪ್ರಕ್ರಿಯೆಗಳಿಗೆ ನಮ್ಮನ್ನು ನಿರ್ಬಂಧಿಸಿದರೆ ವಿಭಿನ್ನ ಸಮೀಕರಣವನ್ನು ಪರಿಹರಿಸಲು ಕಡಿಮೆ ಮಾಡಬಹುದು. ಅಲ್ಪಾವಧಿಯಲ್ಲಿ ಕಡಿಮೆ ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ ಮಾತ್ರ ಗಮನಾರ್ಹ ಚಲನೆಗಳು ಸಾಧ್ಯವಾದರೆ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯನ್ನು ನಿರಂತರ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಹೆಚ್ಚು ನಿಖರವಾಗಿ, ಇದರರ್ಥ ಅದು ಏನೇ ಇರಲಿ

ಸಂಭವನೀಯತೆಯೊಂದಿಗೆ ನಿರಂತರವಾದ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಸಾಕ್ಷಾತ್ಕಾರಗಳು ನಿರಂತರವಾಗಿರುತ್ತವೆ.

ಸಮೀಕರಣದಿಂದ (5.62), ವೇರಿಯೇಬಲ್‌ಗಳ ಪದನಾಮಗಳನ್ನು ಊಹಿಸಿ ಮತ್ತು ಬದಲಾಯಿಸುವುದರಿಂದ, ನಾವು ಪಡೆಯುತ್ತೇವೆ

ಇದಲ್ಲದೆ, ಇದು ಸ್ಪಷ್ಟವಾಗಿದೆ

ಕೊನೆಯ ಎರಡು ಸಮಾನತೆಗಳಿಂದ ಅದು ಅನುಸರಿಸುತ್ತದೆ

ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯನ್ನು ಟೇಲರ್ ಸರಣಿಯಾಗಿ ವಿಸ್ತರಿಸಬಹುದು ಎಂದು ನಾವು ಊಹಿಸೋಣ

(5.80) ಅನ್ನು (5.79) ಗೆ ಬದಲಿಸಿ, ಎರಡೂ ಬದಿಗಳನ್ನು ಭಾಗಿಸಿ ಮತ್ತು ನಾವು ಪಡೆಯುವ ಮಿತಿಗೆ ಹಾದುಹೋಗುವುದು

5.4.8. ಪ್ರಸರಣ ಪ್ರಕ್ರಿಯೆಗಳು.

ಕಾರ್ಯಗಳು ಶೂನ್ಯ ಮತ್ತು ಫಾರ್ ಸೀಮಿತವಾಗಿದ್ದರೆ, ನಿರಂತರ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಪ್ರಸರಣ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. (5.81) ರಿಂದ ಪ್ರಸರಣ ಪ್ರಕ್ರಿಯೆಯ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯು ಭಾಗಶಃ ಭೇದಾತ್ಮಕ ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆ

ವಿಲೋಮ ಕೊಲ್ಮೊಗೊರೊವ್ ಸಮೀಕರಣ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಅಂತೆಯೇ, ಪ್ರಸರಣ ಪ್ರಕ್ರಿಯೆಯ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯು ನೇರ ಕೊಲ್ಮೊಗೊರೊವ್ ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆ ಎಂದು ಸಾಬೀತುಪಡಿಸಬಹುದು:

ಡ್ರಿಫ್ಟ್ ಗುಣಾಂಕ, ಮತ್ತು

ಪ್ರಸರಣ ಗುಣಾಂಕ.

ನೇರ ಕೊಲ್ಮೊಗೊರೊವ್ ಸಮೀಕರಣವನ್ನು (5.84) ಫೋಕರ್-ಪ್ಲಾವ್ಕಾ ಸಮೀಕರಣ ಎಂದೂ ಕರೆಯಲಾಗುತ್ತದೆ. ಸಮೀಕರಣಗಳು (5.83) ಮತ್ತು (5.84) ಪ್ಯಾರಾಬೋಲಿಕ್ ಭಾಗಶಃ ಭೇದಾತ್ಮಕ ಸಮೀಕರಣಗಳ ವರ್ಗಕ್ಕೆ ಸೇರಿವೆ. (5.83) ರಲ್ಲಿ ವೇರಿಯೇಬಲ್‌ಗಳು ಮತ್ತು ವೇರಿಯೇಬಲ್‌ಗಳು y ಮತ್ತು T ಅನ್ನು ಸ್ಥಿತಿಯಲ್ಲಿ ಮಾತ್ರ ಸೇರಿಸಲಾಗಿದೆ. (5.84) ರಲ್ಲಿ ವೇರಿಯೇಬಲ್‌ಗಳು y ಮತ್ತು ಮತ್ತು t ಗಳು ಆರಂಭಿಕ ಸ್ಥಿತಿಯ ಮೂಲಕ ಮಾತ್ರ ಪ್ರವೇಶಿಸುತ್ತವೆ. ಕೊಲ್ಮೊಗೊರೊವ್ನ ಸಮೀಕರಣಗಳನ್ನು ಪರಿಹರಿಸುವ ವಿಧಾನಗಳನ್ನು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ, ಉದಾಹರಣೆಗೆ, .

5.4.9. ಸ್ಥಾಯಿ ಪ್ರಸರಣ ಪ್ರಕ್ರಿಯೆಗಳು.

ಸ್ಥಾಯಿ ಪ್ರಸರಣ ಪ್ರಕ್ರಿಯೆಗಳಿಗೆ, ಡ್ರಿಫ್ಟ್ ಗುಣಾಂಕಗಳು (5.85) ಮತ್ತು ಪ್ರಸರಣ (5.86) ಸಮಯದ ನಿಯತಾಂಕವನ್ನು ಅವಲಂಬಿಸಿರುವುದಿಲ್ಲ ಮತ್ತು ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯು ವ್ಯತ್ಯಾಸವನ್ನು ಅವಲಂಬಿಸಿರುತ್ತದೆ. ನಂತರ (5.84) ನಿಂದ ನಾವು ಪಡೆಯುತ್ತೇವೆ

ಆರಂಭಿಕ ಸ್ಥಿತಿಯೊಂದಿಗೆ

ಆರಂಭಿಕ ಸ್ಥಿತಿಯನ್ನು ಅವಲಂಬಿಸಿರದ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯ ಮೇಲೆ ಮಿತಿ ಇದ್ದರೆ, ಅದನ್ನು ಸ್ಥಾಯಿ ಪ್ರಸರಣ ಪ್ರಕ್ರಿಯೆಯ ಸೀಮಿತಗೊಳಿಸುವ ವಿತರಣಾ ಕಾರ್ಯ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

(5.88) ನಿಂದ ಅದು ಅನುಸರಿಸುತ್ತದೆ. ಆದ್ದರಿಂದ, ಮಿತಿ ವಿತರಣಾ ಕಾರ್ಯವನ್ನು ಮೊದಲ ಕ್ರಮಾಂಕದ ಸಾಮಾನ್ಯ ಭೇದಾತ್ಮಕ ಸಮೀಕರಣದಿಂದ ಕಂಡುಹಿಡಿಯಬಹುದು

ಅವರ ಪರಿಹಾರವು ರೂಪವನ್ನು ಹೊಂದಿದೆ

ಸ್ಥಿರಾಂಕಗಳನ್ನು ಸಾಮಾನ್ಯೀಕರಣ ಸ್ಥಿತಿ ಮತ್ತು ಗಡಿ ಸ್ಥಿತಿಯಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ

5.4.10. ಗಾಸಿಯನ್ ಪ್ರಸರಣ ಪ್ರಕ್ರಿಯೆ.

ಶೂನ್ಯ ಸರಾಸರಿ, ವ್ಯತ್ಯಯ ಮತ್ತು ಸಾಮಾನ್ಯವಾದ ಪರಸ್ಪರ ಸಂಬಂಧ ಕ್ರಿಯೆಯೊಂದಿಗೆ ಗಾಸ್ಸಿಯನ್ ಸ್ಥಾಯಿ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಪರಿಗಣಿಸಿ. ಈ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯ ಷರತ್ತುಬದ್ಧ ವಿತರಣೆ ಸಾಂದ್ರತೆ [ನೋಡಿ (2.74)]

(5.82) ಪ್ರಕಾರ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ಕಾರ್ಯಗಳನ್ನು ಪರಿಗಣನೆಯಡಿಯಲ್ಲಿ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯನ್ನು ಕಂಡುಹಿಡಿಯೋಣ:

(5.92)

ಬಲದಿಂದ ಶೂನ್ಯವನ್ನು ಸಮೀಪಿಸಿದಾಗ ಉತ್ಪನ್ನದ ಮೌಲ್ಯ ಎಲ್ಲಿದೆ. ಶೂನ್ಯದಲ್ಲಿ ನಿರಂತರವಾಗಿದ್ದರೆ, ಅದು ನಲ್ಲಿ ಸ್ಥಗಿತವನ್ನು ಅನುಭವಿಸುತ್ತದೆ ಎಂದು ಊಹಿಸಿ. ನಂತರ

ಈ ವಿಭಾಗದಲ್ಲಿ, ಸೂಕ್ತವಾದ ಡೆಮೋಡ್ಯುಲೇಟರ್ ಅನ್ನು ಕಂಡುಹಿಡಿಯಲು ನಾವು ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆ ವಿಧಾನವನ್ನು ಬಳಸುತ್ತೇವೆ. ನಮ್ಮ ಪ್ರಸ್ತುತಿ ಮೇಲ್ನೋಟಕ್ಕೆ ಇದೆ, ಆದ್ದರಿಂದ ಹೆಚ್ಚು ವಿವರವಾದ ಪರಿಗಣನೆಗಾಗಿ, ಆಸಕ್ತ ಓದುಗರು ಹೆಚ್ಚುವರಿ ಮೂಲಗಳನ್ನು (ನಿರ್ದಿಷ್ಟವಾಗಿ,) ಉಲ್ಲೇಖಿಸಬೇಕು. ಮತ್ತು ಈ ಸಮಯದಲ್ಲಿ ನಾವು ಸಂದೇಶವು ಗೌಸಿಯನ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯಾಗಿದ್ದು, ರಾಜ್ಯ ಅಸ್ಥಿರಗಳಲ್ಲಿ ಸೀಮಿತ ಪ್ರಾತಿನಿಧ್ಯವನ್ನು ಹೊಂದಿದೆ, ಅಂದರೆ.

ಕೋವೇರಿಯನ್ಸ್ ಫಂಕ್ಷನ್‌ನೊಂದಿಗೆ ಬಿಳಿ ಗಾಸಿಯನ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆ ಎಲ್ಲಿದೆ

ನಮ್ಮ ಚರ್ಚೆಯಲ್ಲಿ ನಾವು ಈ ಸತ್ಯವನ್ನು ಬಳಸದಿದ್ದರೂ, ರಾಜ್ಯದ ಸಮೀಕರಣ ಮತ್ತು ವೀಕ್ಷಣಾ ಸಮೀಕರಣವು ರೇಖಾತ್ಮಕವಲ್ಲದ ಮತ್ತು ರೂಪವನ್ನು ಹೊಂದಿರುವಾಗ ಈ ವಿಭಾಗದಲ್ಲಿ ವಿವರಿಸಿದ ಕಾರ್ಯವಿಧಾನವನ್ನು ಸಹ ನಿರ್ವಹಿಸಬಹುದು ಎಂದು ಸೂಚಿಸಬೇಕು.

ಕೆಲವು ನಿರ್ಬಂಧಗಳ ಅಡಿಯಲ್ಲಿ ವೆಕ್ಟರ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯಾಗಿದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ, ಇದು ಗೌಸಿಯನ್ ಆಗಿರಬೇಕಾಗಿಲ್ಲ. ಹಿಂದೆ ಚರ್ಚಿಸಿದ ಯಾವುದೇ ವಿಧಾನಗಳು ಈ ವರ್ಗದ ಸಂದೇಶಗಳೊಂದಿಗೆ ಸಮಸ್ಯೆಗಳನ್ನು ಪರಿಹರಿಸಲು ಅನುಮತಿಸುವುದಿಲ್ಲ. ಈ ವಿಭಾಗದಲ್ಲಿ ಪಡೆಯಲಾಗುವ ಹೆಚ್ಚಿನ ಫಲಿತಾಂಶಗಳನ್ನು ಸಮೀಕರಣಗಳು (78) ಮತ್ತು (79) ವಿವರಿಸಿದ ಹೆಚ್ಚು ಸಾಮಾನ್ಯ ಪ್ರಕ್ರಿಯೆಗೆ ಸಹ ಪಡೆಯಬಹುದು.

ನಾವು ಈಗ ಸಂಬಂಧಗಳು ವಿವರಿಸಿದ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯ ರೂಪದಲ್ಲಿ ಮಾದರಿಗೆ ಹಿಂತಿರುಗೋಣ. ಸಂಕೇತದ ಸರಳತೆಗಾಗಿ, ನಾವು ಸ್ಕೇಲಾರ್ ಗಾಸಿಯನ್ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯ ಸಂದೇಶವನ್ನು ಪರಿಗಣಿಸುತ್ತೇವೆ ಮತ್ತು ಅದರ ಮೂಲಕ ಪ್ರಸರಣ ಆಂದೋಲನವನ್ನು ಕೆಲವು ಜಡತ್ವದಿಂದ ಮಾಡ್ಯುಲೇಟ್ ಮಾಡಲಾಗುತ್ತದೆ. -ಮುಕ್ತ ರೀತಿಯ ಮಾಡ್ಯುಲೇಶನ್. ಸ್ವೀಕರಿಸಿದ ಕಂಪನವನ್ನು ರೂಪದಲ್ಲಿ ಬರೆಯಲಾಗಿದೆ

ಸಂದೇಶ ಪ್ರಕ್ರಿಯೆಯು ಮೊದಲ ಕ್ರಮಾಂಕದ ಭೇದಾತ್ಮಕ ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆ

ಹೀಗಾಗಿ, ಯಾವುದೇ ಸೀಮಿತ ಮೌಲ್ಯಗಳಿಗೆ, ಸಂದೇಶವು ಸ್ಥಾಯಿ ಪ್ರಕ್ರಿಯೆಯಾಗಿದೆ ಮತ್ತು ಮೊದಲ ಕ್ರಮಾಂಕದ ಬಟರ್‌ವರ್ತ್ ಸ್ಪೆಕ್ಟ್ರಮ್ ಅನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಇದಲ್ಲದೆ, ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಯು ಮೊದಲ ಕ್ರಮದಲ್ಲಿದೆ ಎಂಬ ಅಂಶದಿಂದಾಗಿ, ಯಾವುದೇ ಅವಲೋಕನಗಳ ಅನುಪಸ್ಥಿತಿಯಲ್ಲಿ ಅದರ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯು ಫೋಕರ್-ಪ್ಲಾಂಕ್ ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆ [ನೋಡಿ (3.79)]

ಆದಾಗ್ಯೂ, ಸಮಯದ ಮಧ್ಯಂತರದಲ್ಲಿ ಇದನ್ನು ಗಮನಿಸಿದಾಗಿನಿಂದ, ನಮಗೆ ಆಸಕ್ತಿಯ ಸಂಭವನೀಯತೆ ಸಾಂದ್ರತೆಯು ಬೇಷರತ್ತಾದ ಸಾಂದ್ರತೆಯಲ್ಲ, ಆದರೆ ಗಮನಿಸಿದ ಆಂದೋಲನದಿಂದಾಗಿ ಸಾಂದ್ರತೆಯಾಗಿದೆ. ನಾವು ಈ ಸಾಂದ್ರತೆಯನ್ನು ಇದರ ಮೂಲಕ ಸೂಚಿಸೋಣ

(86) ಎಂಬುದು ಒಂದು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್‌ನ ಸಂಭವನೀಯತೆ ಸಾಂದ್ರತೆಯಾಗಿದೆ (ಒಂದು ಮೌಲ್ಯವು ಗಮನಿಸಿದ ಆಂದೋಲನದಿಂದಾಗಿ ಸಮಯದ ಕ್ಷಣದಲ್ಲಿ ಮೌಲ್ಯವನ್ನು ಸೂಚಿಸುತ್ತದೆ, ಮತ್ತು ಇದು ಉತ್ತಮವಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾದ ಗುಣಲಕ್ಷಣವಾಗಿದೆ. ಈ ಸಂಭವನೀಯತೆಯ ಸಾಂದ್ರತೆಯು ಅದನ್ನು ಪೂರೈಸುತ್ತದೆ ಎಂದು ತೋರಿಸಬಹುದು. ಸಮೀಕರಣ

ಅಲ್ಲಿ ಗಣಿತದ ನಿರೀಕ್ಷೆಗಳನ್ನು ಸಾಂದ್ರತೆಯಿಂದ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ, ನಾವು ಔಪಚಾರಿಕವಾಗಿ ಉತ್ಪನ್ನವನ್ನು ಪರಿಚಯಿಸಿದರೆ

ನಂತರ (87) ಅನ್ನು ಔಪಚಾರಿಕವಾಗಿ ವಿಭಿನ್ನ ಸಮೀಕರಣವಾಗಿ ಬರೆಯಬಹುದು

ಹಿಂಭಾಗದ ಸಾಂದ್ರತೆ ಮತ್ತು ಕನಿಷ್ಠ ಸರಾಸರಿ ಚದರ ದೋಷದ ಅಂದಾಜು ನಡುವಿನ ಸಂಬಂಧವು ಚೆನ್ನಾಗಿ ತಿಳಿದಿದೆ. ಕನಿಷ್ಠ ಸರಾಸರಿ ಚದರ ದೋಷದ ಅಂದಾಜು ಹಿಂಭಾಗದ ಸಾಂದ್ರತೆಯ ಷರತ್ತುಬದ್ಧ ಸರಾಸರಿಯಾಗಿದೆ (ಮೊದಲ ಸಂಪುಟದ ಪುಟ 73 ನೋಡಿ), ಅಂದರೆ.

(89) ನ ಎರಡೂ ಬದಿಗಳನ್ನು A ಯಿಂದ ಗುಣಿಸಿ, ಮಧ್ಯಂತರದ ಅಂತ್ಯದಲ್ಲಿ ಅನುಗುಣವಾದ ಪರಿಸ್ಥಿತಿಗಳನ್ನು ಸಂಯೋಜಿಸಿ ಮತ್ತು ಗಣನೆಗೆ ತೆಗೆದುಕೊಂಡು, ನಾವು ಪಡೆಯುತ್ತೇವೆ (ಸಮಸ್ಯೆ 7.2.2 ನೋಡಿ)

(91) ಇನ್ನೂ ನಿರೀಕ್ಷಿತ ಗಣಿತದ ನಿರೀಕ್ಷೆಯನ್ನು ಹೊಂದಿದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ, ಸಮನ್ವಯತೆಯ ಸಾಮಾನ್ಯ ಪ್ರಕರಣಕ್ಕೆ ಈ ಸಮೀಕರಣವನ್ನು ಪರಿಹರಿಸಲಾಗುವುದಿಲ್ಲ. ಲೀನಿಯರ್ ಮಾಡ್ಯುಲೇಶನ್ ವಿಧಾನಗಳ ಸಂದರ್ಭದಲ್ಲಿ, ಅದನ್ನು ತೋರಿಸಲು ಸುಲಭವಾಗಿದೆ (ಉದಾಹರಣೆಗೆ, 18] ಅಥವಾ ಸಮಸ್ಯೆ 7.2.1) ಇದನ್ನು ಕಡಿಮೆ ಮಾಡುತ್ತದೆ ಅನೇಕ ರೇಖಾತ್ಮಕವಲ್ಲದ ಮಾಡ್ಯುಲೇಶನ್ ಸಮಸ್ಯೆಗಳಿಗೆ, ವಿಭಿನ್ನ ಸಮೀಕರಣದ ಪದಗಳ ಸರಣಿಯನ್ನು ವಿಸ್ತರಿಸುವ ಮೂಲಕ ಯಶಸ್ಸನ್ನು ಸಾಧಿಸಬಹುದು ( 91) ನಂತರ, ಅಂದಾಜು ದೋಷವು ಚಿಕ್ಕದಾಗಿದೆ ಎಂದು ನಾವು ಭಾವಿಸಿದರೆ ಮತ್ತು ಹೆಚ್ಚಿನ ಆದೇಶಗಳ ಕ್ಷಣಗಳಲ್ಲಿ ಕೆಲವು ಷರತ್ತುಗಳನ್ನು ವಿಧಿಸಿದರೆ, ನಾವು ಎರಡನೇ ಮತ್ತು ಹೆಚ್ಚಿನ ಆದೇಶಗಳ ನಿಯಮಗಳನ್ನು ನಿರ್ಲಕ್ಷಿಸಬಹುದು ಮತ್ತು ಕೆಳಗಿನ ಅಂದಾಜು ಸಮೀಕರಣವನ್ನು ಪಡೆಯಬಹುದು (ಪುಸ್ತಕದ ಅಧ್ಯಾಯ 4 ರಲ್ಲಿ ವಿವರವಾದ ವ್ಯುತ್ಪನ್ನವನ್ನು ನೀಡಲಾಗಿದೆ. ):

ಅಲ್ಲಿ ಕನಿಷ್ಠ ಸರಾಸರಿ ಚದರ ದೋಷದ ಆಧಾರದ ಮೇಲೆ ಅಂದಾಜು ಅಂದಾಜನ್ನು ಸೂಚಿಸುತ್ತದೆ. ಕಾರ್ಯವು ಅಂದಾಜು ಷರತ್ತುಬದ್ಧವಾಗಿದೆ [ಸರಾಸರಿ ವರ್ಗ ದೋಷದ ಪ್ರಕಾರ, ಇದು ವಿಭಿನ್ನ ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆ

ಗಡಿ ಸ್ಥಿತಿಯೊಂದಿಗೆ

ಅಂದಾಜು ಸಮೀಕರಣ (92) ಮತ್ತು ಪ್ರಸರಣ ಸಮೀಕರಣ (93) ಸಂಬಂಧಿಸಿವೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ. ಷರತ್ತುಬದ್ಧ ಮೂಲವು ಚದರ ದೋಷವನ್ನು ಅರ್ಥೈಸುತ್ತದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ [ಅಂದರೆ. e. ದೋಷ, ದೋಷವು ಚಿಕ್ಕದಾಗಿದ್ದಾಗ ಸ್ವೀಕರಿಸಲು ಮಾಡಬೇಕಾದ ಅಂದಾಜುಗಳು ಮಾನ್ಯವಾಗಿರುತ್ತವೆ.

ಅಂಜೂರದಲ್ಲಿ ತೋರಿಸಿರುವ ಬ್ಲಾಕ್ ರೇಖಾಚಿತ್ರದ ರೂಪದಲ್ಲಿ ಸಮೀಕರಣವನ್ನು (92) ಕಾರ್ಯಗತಗೊಳಿಸಬಹುದು ಎಂದು ನಾವು ನೋಡುತ್ತೇವೆ. 7.3 ಈ ಅಳವಡಿಕೆಯು ಅಧ್ಯಾಯದಲ್ಲಿ ಸಂಶ್ಲೇಷಿಸಲಾದ ಗರಿಷ್ಟ ಹಿಂಭಾಗದ ಸಂಭವನೀಯತೆಯ ಅಂದಾಜಿನ ರಚನೆಯನ್ನು ಹೋಲುತ್ತದೆ. 2, ಒಂದೇ ವ್ಯತ್ಯಾಸದೊಂದಿಗೆ ಈಗ ಲೂಪ್‌ನಲ್ಲಿರುವ ಫಿಲ್ಟರ್ ಸ್ವಯಂಚಾಲಿತವಾಗಿ ಕಾರ್ಯಗತಗೊಳ್ಳುತ್ತದೆ. ಈ ಅನುಷ್ಠಾನದ ಅನನುಕೂಲವೆಂದರೆ ಲೂಪ್ಗಳ ನಡುವಿನ ಸಂವಹನದ ಉಪಸ್ಥಿತಿ.

ಕೋನೀಯ ಸಮನ್ವಯತೆಯ ಸಂದರ್ಭದಲ್ಲಿ, ಈ ಜೋಡಣೆಯನ್ನು ಸಾಮಾನ್ಯವಾಗಿ ನಿರ್ಲಕ್ಷಿಸಬಹುದು ಎಂದು ತೋರಿಸಬಹುದು. ಉದಾಹರಣೆಗೆ, ಹಂತದ ಸಮನ್ವಯತೆಯೊಂದಿಗೆ

ಸಂದೇಶ ಸ್ಪೆಕ್ಟ್ರಮ್‌ನಲ್ಲಿನ ಅತ್ಯಧಿಕ ಆವರ್ತನಕ್ಕಿಂತ ಇದು ಹೆಚ್ಚಿನದಾಗಿದೆ ಮತ್ತು ಸಿಸ್ಟಮ್ ಸಂಖ್ಯಾಶಾಸ್ತ್ರೀಯವಾಗಿ ಸ್ಥಿರ ಸ್ಥಿತಿಯಲ್ಲಿದೆ ಎಂದು ಊಹಿಸಲಾಗಿದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ ಅದನ್ನು ತೋರಿಸಲಾಗಿದೆ

ಬದಲಿ ಮಾಡುವಾಗ ಪ್ರಸರಣ ಸಮೀಕರಣವನ್ನು ಪೂರೈಸುತ್ತದೆ

ಮೊದಲ ಕ್ರಮಾಂಕದ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಾಗಿ, ಈ ಸಮೀಕರಣವು ರೂಪವನ್ನು ಹೊಂದಿದೆ

ರಿಸೀವರ್ನ ಬ್ಲಾಕ್ ರೇಖಾಚಿತ್ರವನ್ನು ಅಂಜೂರದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ. 7.4. ಈ ರಚನೆಯು ಅಂದಾಜು ಗರಿಷ್ಟ ಹಿಂಭಾಗದ ಸಂಭವನೀಯತೆಯ ರಿಸೀವರ್‌ನ ಕಾರ್ಯಗತಗೊಳಿಸಿದ ಭಾಗದೊಂದಿಗೆ ನಿಖರವಾಗಿ ಹೊಂದಿಕೆಯಾಗುತ್ತದೆ, ಇದನ್ನು ಮೊದಲೇ ಸಂಶ್ಲೇಷಿಸಲಾಗಿದೆ ((68) ನಲ್ಲಿನ ಸಮಸ್ಯೆಯನ್ನು ನೋಡಿ) ಈಗ ಅಂದಾಜು ಷರತ್ತುಬದ್ಧ ಸರಾಸರಿ ಚೌಕ ದೋಷ ಎಂದು ಅರ್ಥೈಸಬಹುದು.

ಅಕ್ಕಿ. 7.4. ಆಪ್ಟಿಮಲ್ ರಿಸೀವರ್: ಹಂತದ ಮಾಡ್ಯುಲೇಶನ್, ಮೊದಲ ಆರ್ಡರ್ ಬಟರ್‌ವರ್ತ್ ಸ್ಪೆಕ್ಟ್ರಮ್‌ನೊಂದಿಗೆ ಸಂವಹನ.

ಔಟ್‌ಪುಟ್‌ನ ಹೆಚ್ಚಿನ ವಿವರಗಳನ್ನು ಬಿಟ್ಟುಬಿಡಲಾಗಿರುವುದರಿಂದ, ಫಲಿತಾಂಶದ ಮಿತಿಗಳನ್ನು ಗಮನಿಸುವುದು ಮುಖ್ಯವಾಗಿದೆ. ಷರತ್ತುಬದ್ಧ ಸರಾಸರಿಯನ್ನು ನಿರ್ಧರಿಸುವ ಡಿಫರೆನ್ಷಿಯಲ್ ಸಮೀಕರಣ (91), ನಿಖರವಾಗಿದೆ. ಆದಾಗ್ಯೂ, (92)-(93) ಪಡೆಯುವುದರೊಂದಿಗೆ ಸಂಬಂಧಿಸಿದ ಅಂದಾಜುಗಳು ರೇಖಾತ್ಮಕಗೊಳಿಸುವ ಊಹೆಗೆ ಅನುಗುಣವಾಗಿರುತ್ತವೆ. ಆದ್ದರಿಂದ, ನಮ್ಮ ಫಲಿತಾಂಶವು ನಿಖರವಾದ ಅಂದಾಜಿನ ಸರಣಿ ವಿಸ್ತರಣೆಯ ಮೊದಲ ಅವಧಿಗೆ ಅನುಗುಣವಾದ ಕನಿಷ್ಠ ಸರಾಸರಿ ಚದರ ದೋಷದ ಆಧಾರದ ಮೇಲೆ ಅಂದಾಜು ಅಂದಾಜು ಆಗಿದೆ. ಉತ್ತಮ ಅಂದಾಜನ್ನು ಪಡೆಯಲು, ಹೆಚ್ಚಿನ ಸಂಖ್ಯೆಯ ವಿಸ್ತರಣೆ ನಿಯಮಗಳನ್ನು ಉಳಿಸಿಕೊಳ್ಳಬಹುದು (ಉದಾಹರಣೆಗೆ, ನೋಡಿ). ಈ ಕಾರ್ಯವಿಧಾನದ ತೊಂದರೆ ಎಂದರೆ ಎರಡು-ಅವಧಿಯ ಅಂದಾಜು ಈಗಾಗಲೇ ತುಂಬಾ ಸಂಕೀರ್ಣವಾಗಿದೆ, ಅದು ಬಹುಶಃ ಪ್ರಾಯೋಗಿಕ ಆಸಕ್ತಿಯನ್ನು ಹೊಂದಿಲ್ಲ.

ಕೆಲವು ವ್ಯವಸ್ಥೆಯಲ್ಲಿ ಒಂದು s.p. ಸಂಭವಿಸಲಿ. ಪ್ರತ್ಯೇಕ ರಾಜ್ಯಗಳೊಂದಿಗೆ
ಮತ್ತು ಪ್ರತ್ಯೇಕ ಸಮಯ, ಅಂದರೆ. ಒಂದು ರಾಜ್ಯದಿಂದ ಇನ್ನೊಂದಕ್ಕೆ ವ್ಯವಸ್ಥೆಯ ಪರಿವರ್ತನೆಯು ನಿರ್ದಿಷ್ಟ ಸಮಯದಲ್ಲಿ ಮಾತ್ರ ಸಂಭವಿಸುತ್ತದೆ
. ಈ ಕ್ಷಣಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಹಂತಗಳುಪ್ರಕ್ರಿಯೆ (ಸಾಮಾನ್ಯವಾಗಿ ಪಕ್ಕದ ವೀಕ್ಷಣಾ ಕ್ಷಣಗಳ ನಡುವಿನ ವ್ಯತ್ಯಾಸ
ಸ್ಥಿರ ಸಂಖ್ಯೆಗೆ ಸಮನಾಗಿರುತ್ತದೆ - ಸಮಯದ ಒಂದು ಘಟಕವಾಗಿ ತೆಗೆದುಕೊಂಡ ಹಂತದ ಉದ್ದ);
ಪ್ರಕ್ರಿಯೆಯ ಪ್ರಾರಂಭ.

ಈ ಎಸ್.ಪಿ. ಘಟನೆಗಳ ಅನುಕ್ರಮ (ಸರಪಳಿ) ಎಂದು ಪರಿಗಣಿಸಬಹುದು
.

ವ್ಯವಸ್ಥೆಯ ಆರಂಭಿಕ ಸ್ಥಿತಿ, ಅಂದರೆ. 1 ನೇ ಹಂತದ ಮೊದಲು;
1 ನೇ ಹಂತದ ನಂತರ ವ್ಯವಸ್ಥೆಯ ಸ್ಥಿತಿ,
2 ನೇ ಹಂತದ ನಂತರ ವ್ಯವಸ್ಥೆಯ ಸ್ಥಿತಿ, ಇತ್ಯಾದಿ), ಅಂದರೆ. ಮುಂತಾದ ಘಟನೆಗಳು
ಎಲ್ಲಿ.

ಪ್ರತ್ಯೇಕ ರಾಜ್ಯಗಳು ಮತ್ತು ಪ್ರತ್ಯೇಕ ಸಮಯವನ್ನು ಹೊಂದಿರುವ ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಮಾರ್ಕೋವ್ ಸರಣಿ(ಮಾರ್ಕೊವ್ ಸರಣಿ).

ಎಂಬುದನ್ನು ಗಮನಿಸಿ ಮಾರ್ಕೋವ್ ಸರಣಿ, ಇದರಲ್ಲಿ ಭವಿಷ್ಯದಲ್ಲಿ ರಾಜ್ಯಗಳ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆಗಳು ಕೊನೆಯ ಹಂತದಲ್ಲಿ (ಮತ್ತು ಹಿಂದಿನವುಗಳ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿಲ್ಲ) ರಾಜ್ಯದ ಮೇಲೆ ಮಾತ್ರ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ ಸರಳ ಮಾರ್ಕೊವ್ ಸರಣಿ. (ಎ.ಎ. ಮಾರ್ಕೊವ್ 1856-1922 - ರಷ್ಯಾದ ಗಣಿತಜ್ಞ).

ಅಂತಹ ವ್ಯವಸ್ಥೆಯ ಉದಾಹರಣೆ ತಾಂತ್ರಿಕ ಸಾಧನವಾಗಿ ಕಾರ್ಯನಿರ್ವಹಿಸಬಹುದು, ಅದರ ಸಂಭವನೀಯ ಸ್ಥಿತಿಗಳು ಈ ಕೆಳಗಿನಂತಿವೆ:

ಒಳ್ಳೆಯ ಕೆಲಸ;

ತಡೆಗಟ್ಟುವ ತಪಾಸಣೆ ಮತ್ತು ನಿರ್ವಹಣೆ;

ನವೀಕರಣ ಕೆಲಸ;

ಬಳಕೆಯಾಗದ ಕಾರಣ ಬರೆಯುವಿಕೆ;

ಕೆಲಸದ ಸ್ಥಿತಿಯ ಗ್ರಾಫ್ ಅನ್ನು ಚಿತ್ರದಲ್ಲಿ ತೋರಿಸಲಾಗಿದೆ

ಅಕ್ಕಿ. 1.11.(A.A. ಬೆಲೋವ್, ಇತ್ಯಾದಿ)

ಗ್ರಾಫ್ನ ವಿಶ್ಲೇಷಣೆಯಿಂದ ಶೃಂಗದ ಸಾಮಾನ್ಯ ಕಾರ್ಯಾಚರಣೆಯ ಸ್ಥಿತಿಯಿಂದ ಸ್ಪಷ್ಟವಾಗುತ್ತದೆ ವ್ಯವಸ್ಥೆಯು ತಡೆಗಟ್ಟುವ ನಿರ್ವಹಣೆ ಸ್ಥಿತಿಯನ್ನು ಪ್ರವೇಶಿಸಬಹುದು , ತದನಂತರ ಹಿಂತಿರುಗಿ . ಅಥವಾ ಅಲ್ಲಿಂದ ಸರಿಸಿ ದುರಸ್ತಿ ಸ್ಥಿತಿಯಲ್ಲಿ , ಅದರ ನಂತರ ಅದು ಹಿಂತಿರುಗುತ್ತದೆ , ಅಥವಾ ರೈಟ್-ಆಫ್ ಸ್ಥಿತಿಗೆ ಹೋಗಿ. ರಾಜ್ಯ ಸೀಮಿತವಾಗಿದೆ, ಏಕೆಂದರೆ ಅದರಿಂದ ಪರಿವರ್ತನೆ ಅಸಾಧ್ಯ. ನಿಂದ ಪರಿವರ್ತನೆ ಮರಳಿ ಒಳಗೆ ಈ ಸ್ಥಿತಿಯಲ್ಲಿ ವಿಳಂಬ ಎಂದರ್ಥ.

ಪ್ರಾಯೋಗಿಕವಾಗಿ, ಪ್ರತಿಯೊಂದು ರಾಜ್ಯವು ಸರಪಳಿಯನ್ನು ರೂಪಿಸುವ ವ್ಯವಸ್ಥೆಗಳನ್ನು ನಾವು ಸಾಮಾನ್ಯವಾಗಿ ಎದುರಿಸುತ್ತೇವೆ (ತೀವ್ರವನ್ನು ಹೊರತುಪಡಿಸಿ ಮತ್ತು ) ಎರಡು ನೆರೆಹೊರೆಯವರೊಂದಿಗೆ ನೇರ ಮತ್ತು ಪ್ರತಿಕ್ರಿಯೆ ಸಂಪರ್ಕಗಳ ಮೂಲಕ ಸಂಪರ್ಕ ಹೊಂದಿದೆ,
ಮತ್ತು ವಿಪರೀತ ರಾಜ್ಯಗಳು - ಒಬ್ಬ ನೆರೆಹೊರೆಯವರೊಂದಿಗೆ (ಚಿತ್ರ ನೋಡಿ)

ಚಿತ್ರ.1.12(ಪ್ರೀತಿಯ...)

ಅಂತಹ ಒಂದು ವ್ಯವಸ್ಥೆಯ ಉದಾಹರಣೆಯು ಒಂದೇ ರೀತಿಯ ಘಟಕಗಳನ್ನು ಒಳಗೊಂಡಿರುವ ತಾಂತ್ರಿಕ ಸಾಧನವಾಗಿದೆ. ಪ್ರತಿಯೊಂದು ಸಿಸ್ಟಮ್ ಸ್ಥಿತಿಯನ್ನು ದೋಷಯುಕ್ತ ಸಂಖ್ಯೆಯಿಂದ ನಿರೂಪಿಸಲಾಗಿದೆ ಪರಿಶೀಲನೆಯ ಸಮಯದಲ್ಲಿ ನೋಡ್‌ಗಳು.

ರಾಜ್ಯದ ಸಂಭವನೀಯತೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಅಧ್ಯಯನದ ಮುಖ್ಯ ಉದ್ದೇಶವಾಗಿದೆ ಯಾವುದೇ ಮೇಲೆ
ಮೀ ಹೆಜ್ಜೆ. ಪ್ರತ್ಯೇಕ ವ್ಯವಸ್ಥೆಯ ರಾಜ್ಯಗಳ ಸಂಭವನೀಯತೆಯನ್ನು ನಾವು ಲೆಕ್ಕಾಚಾರ ಮಾಡುತ್ತೇವೆ

ಇಲ್ಲಿ ನಾವು ಸರಳವಾದ ಮಾರ್ಕೊವ್ ಸರಪಳಿಗಳನ್ನು ಮಾತ್ರ ಪರಿಗಣಿಸುತ್ತೇವೆ. ಇದಲ್ಲದೆ, ನಿರಂತರ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಳ ಪರಿಕಲ್ಪನೆಗಳನ್ನು ನಾವು ಸಂಕ್ಷಿಪ್ತವಾಗಿ ಪರಿಗಣಿಸುತ್ತೇವೆ.

ಸಿಸ್ಟಮ್ ಸ್ಟೇಟ್ಸ್ನಲ್ಲಿ ಪ್ರತ್ಯೇಕ ಸಮಯದ ಬದಲಾವಣೆಗಳೊಂದಿಗೆ, ಒಂದು ರಾಜ್ಯದಿಂದ ಇನ್ನೊಂದಕ್ಕೆ ಪ್ರತಿ ಪರಿವರ್ತನೆಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಹಂತ.

ಮಾರ್ಕೊವ್ ಸರಪಳಿಯ ವ್ಯಾಖ್ಯಾನದಿಂದ ಅದು ಸಿಸ್ಟಮ್ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯನ್ನು ಅನುಸರಿಸುತ್ತದೆ ಒಂದು ಸ್ಥಿತಿಯಲ್ಲಿ
ಮೀ ಹಂತವು ರಾಜ್ಯದ ಮೇಲೆ ಮಾತ್ರ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ ವ್ಯವಸ್ಥೆಯು ಹಿಂದಿನದಾಗಿತ್ತು
ಹಂತ.

ಎಲ್ಲಿ
ಬೇಷರತ್ತಾದ ಸಂಭವನೀಯತೆ
ಮೊದಲ ಹಂತದಲ್ಲಿ ಈ ವ್ಯವಸ್ಥೆ ರಾಜ್ಯದಲ್ಲಿರಲಿದೆ . ಈ ಸಂಭವನೀಯತೆಗಳನ್ನು ಕಂಡುಹಿಡಿಯಲು, ಆರಂಭಿಕ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯನ್ನು ತಿಳಿದುಕೊಳ್ಳುವುದು ಅವಶ್ಯಕ, ಅಂದರೆ. ರಾಜ್ಯದ ಸಂಭವನೀಯತೆಗಳು
ಒಂದು ಸಮಯದಲ್ಲಿ
(ಪ್ರಕ್ರಿಯೆಯ ಪ್ರಾರಂಭ) ಮತ್ತು ಕರೆಯಲ್ಪಡುವ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಗಳು
ಮಾರ್ಕೋವ್ ಚೈನ್ ಆನ್
ಮೀ ಹೆಜ್ಜೆ.

ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆ
ಸಿಸ್ಟಮ್ನ ಷರತ್ತುಬದ್ಧ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮೇಲೆ

ಮೀ ಹೆಜ್ಜೆ, ಒಂದು ರಾಜ್ಯದಲ್ಲಿ
ಮೀ ಹೆಜ್ಜೆ ಅವಳು ಸಾಧ್ಯವಾಯಿತು , ಅಂದರೆ

(43),

ಮೊದಲ ಸೂಚ್ಯಂಕವು ಹಿಂದಿನ ಸ್ಥಿತಿಯ ಸಂಖ್ಯೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ ಮತ್ತು ಎರಡನೇ ಸೂಚ್ಯಂಕವು ಸಿಸ್ಟಮ್ನ ನಂತರದ ಸ್ಥಿತಿಯ ಸಂಖ್ಯೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ಮಾರ್ಕೋವ್ ಸರಪಳಿಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಏಕರೂಪದ, ಮೌಲ್ಯವಾಗಿದ್ದರೆ
ಆ. ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆಗಳು
ಪರೀಕ್ಷಾ ಸಂಖ್ಯೆಯನ್ನು ಅವಲಂಬಿಸಬೇಡಿ, ಇಲ್ಲದಿದ್ದರೆ ಅದನ್ನು ಭಿನ್ನಜಾತಿ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಇದಲ್ಲದೆ, ವೆಕ್ಟರ್ ಅನ್ನು ಬಳಸಿಕೊಂಡು ನಿರ್ದಿಷ್ಟಪಡಿಸಬಹುದಾದ ಏಕರೂಪದ ಸರಪಳಿಗಳನ್ನು ಮಾತ್ರ ನಾವು ಪರಿಗಣಿಸುತ್ತೇವೆ - ಒಂದು ಸಮಯದಲ್ಲಿ ರಾಜ್ಯಗಳ ಸಂಭವನೀಯತೆ
ಮತ್ತು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ( ಪರಿವರ್ತನೆಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ)

(44)
.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅಂಶಗಳು
ಸಾಮಾನ್ಯ ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್‌ಗಳ ಮೂಲ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಮತ್ತು ಹೆಚ್ಚುವರಿಯಾಗಿ ಈ ಕೆಳಗಿನ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿವೆ:

ಎ)
, ಬಿ)
ಪ್ರತಿ ಸ್ಥಿರಕ್ಕೆ
, ಅಂದರೆ ಪ್ರತಿ ಸಾಲಿನ ಅಂಶಗಳ ಮೊತ್ತ ಪರಿವರ್ತನೆಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ಒಂದಕ್ಕೆ ಸಮ (ಒಂದು ರಾಜ್ಯದಿಂದ ಪರಿವರ್ತನೆಯ ಘಟನೆಗಳ ಸಂಭವನೀಯತೆ ಯಾವುದೇ ಇತರ ಸಂಭವನೀಯ ಸ್ಥಿತಿಗೆ - ಘಟನೆಗಳ ಸಂಪೂರ್ಣ ಗುಂಪನ್ನು ರೂಪಿಸುವುದು).

ಮುಂದಿನ ಹಂತದಲ್ಲಿ ಸಿಸ್ಟಮ್ ಸ್ಥಿತಿಯ ಸಂಭವನೀಯತೆಯನ್ನು ಮರುಕಳಿಸುವ ಸೂತ್ರದಿಂದ ನಿರ್ಧರಿಸಲಾಗುತ್ತದೆ:

ಕೆಲವು ಪರಿಸ್ಥಿತಿಗಳಲ್ಲಿ (ಎರ್ಗೋಡಿಸಿಟಿ, ಏಕರೂಪತೆ, ಚಕ್ರಗಳ ಅನುಪಸ್ಥಿತಿ) ಮಾರ್ಕೊವ್ ಸರಪಳಿಯನ್ನು ಸ್ಥಾಪಿಸುತ್ತದೆ ಸ್ಥಾಯಿ ಮೋಡ್, ಇದರಲ್ಲಿ ಸಿಸ್ಟಮ್ ಸ್ಟೇಟ್‌ಗಳ ಸಂಭವನೀಯತೆಗಳು ಹಂತದ ಸಂಖ್ಯೆಯನ್ನು ಅವಲಂಬಿಸಿರುವುದಿಲ್ಲ. ಅಂತಹ ಸಂಭವನೀಯತೆಗಳನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ವಿಪರೀತ(ಅಥವಾ ಅಂತಿಮ) ಮಾರ್ಕೊವ್ ಸರಣಿ ಸಂಭವನೀಯತೆಗಳು:

.

ಒಂದು ಸಮರ್ಥನೆ ಇದೆ.

ಪ್ರಮೇಯ 17.1.ಫಾರ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಮೀರಿದ ಸಂಭವನೀಯತೆಗಳ ಪರಿವರ್ತನೆ ಹಂತಗಳು
ಸೂತ್ರವು ಮಾನ್ಯವಾಗಿದೆ

(45)
,

ಪುರಾವೆ.ಎರಡು ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಗುಣಿಸುವ ನಿಯಮದ ಪ್ರಕಾರ
ನಾವು ಹೊಂದಿರುವ ನೇ ಕ್ರಮದಲ್ಲಿ

ಎಲ್ಲಿ

ಇದಲ್ಲದೆ, ಪರಿವರ್ತನೆಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ನ ವ್ಯಾಖ್ಯಾನದಿಂದ ಅದು ತಿಳಿದಿದೆ
ಯಾವುದೇ ಸಮಯದಲ್ಲಿ
.

ಸಮಾನತೆಯ ಎರಡೂ ಬದಿಗಳನ್ನು ಒಟ್ಟುಗೂಡಿಸೋಣ
ಎಲ್ಲಾ ಮೇಲೆ
, ಮತ್ತು ಆಸ್ತಿಯನ್ನು ಅನ್ವಯಿಸಿದ ನಂತರ ಸಂಕಲನದ ಕ್ರಮವನ್ನು ಬದಲಿಸಿ a) ಎರಡು ಬಾರಿ, ನಾವು ಅದನ್ನು ಪಡೆಯುತ್ತೇವೆ
ಎರಡು ಹಂತಗಳಲ್ಲಿ ಪರಿವರ್ತನೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್. ಅಂತೆಯೇ, ಸತತವಾಗಿ ಹಂತ ಹಂತವಾಗಿ ತಾರ್ಕಿಕವಾಗಿ, ನಾವು ಸಾಮಾನ್ಯ ಪ್ರಕರಣದಲ್ಲಿ ನಮ್ಮ ಹೇಳಿಕೆಯನ್ನು ಪಡೆಯುತ್ತೇವೆ.

ಉದಾಹರಣೆ 3.ಪರಿವರ್ತನೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ನಿರ್ದಿಷ್ಟಪಡಿಸಲಾಗಿದೆ

.

ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಹುಡುಕಿ
.

ಎರಡು ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಗುಣಿಸುವ ನಿಯಮವನ್ನು ಆಧರಿಸಿ, ನಾವು ಪಡೆಯುತ್ತೇವೆ

.

ವ್ಯಾಯಾಮ.ಸಮಾನತೆ ನಿಜವಾಗಿದೆಯೇ ಎಂದು ಪರಿಶೀಲಿಸಿ

ಸೀಮಿತವಾದ ಪ್ರತ್ಯೇಕವಾದ ಮಾರ್ಕೊವ್ ಸರಪಳಿಯು ಬರ್ನೌಲ್ಲಿ ಯೋಜನೆಯ ಮತ್ತಷ್ಟು ಸಾಮಾನ್ಯೀಕರಣವನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ ಎಂದು ಗಮನಿಸಬೇಕು, ಮೇಲಾಗಿ, ಅವಲಂಬಿತ ಪರೀಕ್ಷೆಗಳ ಸಂದರ್ಭದಲ್ಲಿ; ಸ್ವತಂತ್ರ ಪರೀಕ್ಷೆಗಳು ಮಾರ್ಕೊವ್ ಸರಪಳಿಯ ವಿಶೇಷ ಪ್ರಕರಣವಾಗಿದೆ. ಇಲ್ಲಿ "ಈವೆಂಟ್" ಅಡಿಯಲ್ಲಿ

ವ್ಯವಸ್ಥೆಯ ಸ್ಥಿತಿಯನ್ನು ಸೂಚಿಸುತ್ತದೆ ಮತ್ತು "ಪರೀಕ್ಷೆ" ವ್ಯವಸ್ಥೆಯ ಸ್ಥಿತಿಯಲ್ಲಿನ ಬದಲಾವಣೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ.

ಒಂದು ವೇಳೆ " ಪರೀಕ್ಷೆಗಳು"(ಪ್ರಯೋಗಗಳು) ಸ್ವತಂತ್ರವಾಗಿರುತ್ತವೆ, ನಂತರ ಯಾವುದೇ ಪ್ರಯೋಗದಲ್ಲಿ ಒಂದು ನಿರ್ದಿಷ್ಟ ಘಟನೆಯ ಸಂಭವವು ಹಿಂದೆ ನಡೆಸಿದ ಪರೀಕ್ಷೆಗಳ ಫಲಿತಾಂಶಗಳನ್ನು ಅವಲಂಬಿಸಿರುವುದಿಲ್ಲ.

ಕಾರ್ಯಗಳು. a) ಪರಿವರ್ತನೆಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನೀಡಲಾಗಿದೆ

1.
;

2.
;

3.
.

ಪ್ರತಿ ಸಂದರ್ಭದಲ್ಲಿ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅನ್ನು ಹುಡುಕಿ
.

ಉತ್ತರಗಳು: a) 1.
;

2.
;

3.

ಸಿ) ಪರಿವರ್ತನೆಯ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ನೀಡಲಾಗಿದೆ

;
.

ಹುಡುಕಿ
.

ಉತ್ತರಗಳು: ಸಿ) 1.
;2.
;

3.
.

ಕಾಮೆಂಟ್ ಮಾಡಿ.ಸಾಮಾನ್ಯವಾಗಿ, ಪ್ರತ್ಯೇಕ ಮಾರ್ಕೋವ್ ಸರಣಿ
ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯಾಗಿದ್ದು, ಅದರ ಸ್ಥಿತಿಯ ಸ್ಥಳವು ಸೀಮಿತವಾಗಿದೆ ಅಥವಾ ಎಣಿಕೆಯಾಗುತ್ತದೆ, ಮತ್ತು ಸೂಚ್ಯಂಕಗಳ ಸೆಟ್
- ಎಲ್ಲಾ ಋಣಾತ್ಮಕವಲ್ಲದ ಪೂರ್ಣಾಂಕಗಳ ಸೆಟ್ ಅಥವಾ ಅದರ ಕೆಲವು ಉಪವಿಭಾಗಗಳು (ಸೀಮಿತ ಅಥವಾ ಎಣಿಸಬಹುದಾದ). ನಾವು ಮಾತನಾಡಬಹುದು ಫಲಿತಾಂಶದ ಬಗ್ಗೆ ಹೇಗೆ
ನೇ ಪರೀಕ್ಷೆಗಳು.

ಋಣಾತ್ಮಕವಲ್ಲದ ಪೂರ್ಣಾಂಕಗಳ ಗುಂಪಿನೊಂದಿಗೆ ಪ್ರಕ್ರಿಯೆಯ ಸ್ಥಿತಿಯ ಸ್ಥಳವನ್ನು ಗುರುತಿಸಲು ಇದು ಸಾಮಾನ್ಯವಾಗಿ ಅನುಕೂಲಕರವಾಗಿರುತ್ತದೆ
ಮತ್ತು ಈ ಸಂದರ್ಭಗಳಲ್ಲಿ ಅವರು ಹೇಳುತ್ತಾರೆ ಒಂದು ಸ್ಥಿತಿಯಲ್ಲಿದೆ , ವೇಳೆ
.

ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ ಅನ್ನು ಹೊಡೆಯುವ ಸಂಭವನೀಯತೆ
ಒಂದು ರಾಜ್ಯದಲ್ಲಿ (ಒಂದು ಹಂತದ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ), ಮೇಲೆ ಹೇಳಿದಂತೆ, ಸೂಚಿಸಲಾಗುತ್ತದೆ
, ಅಂದರೆ

ಈ ಸಂಕೇತವು ಸಾಮಾನ್ಯ ಸಂದರ್ಭದಲ್ಲಿ, ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಗಳು ಆರಂಭಿಕ ಮತ್ತು ಅಂತಿಮ ಸ್ಥಿತಿಗಳ ಮೇಲೆ ಮಾತ್ರವಲ್ಲದೆ ಪರಿವರ್ತನೆಯ ಕ್ಷಣದ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ ಎಂದು ಒತ್ತಿಹೇಳುತ್ತದೆ.

ಒಂದು-ಹಂತದ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಗಳು ಸಮಯ ವೇರಿಯಬಲ್ ಅನ್ನು ಅವಲಂಬಿಸಿರದ ಸಂದರ್ಭಗಳಲ್ಲಿ (ಅಂದರೆ, ಮೌಲ್ಯದ ಮೇಲೆ , ನಂತರ ಅವರು ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆ ಹೊಂದಿದೆ ಎಂದು ಹೇಳುತ್ತಾರೆ ಸ್ಥಾಯಿ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಗಳು. ಆದ್ದರಿಂದ, ಮುಂದಿನ ಉದ್ದೇಶಗಳಿಗಾಗಿ, ಅವಲಂಬಿಸದ ಸಮಾನತೆ ಇದೆ ಎಂದು ನಾವು ಗಮನಿಸುತ್ತೇವೆ , ಮತ್ತು ರಾಜ್ಯದಿಂದ ಒಂದು ಪ್ರಯೋಗದಲ್ಲಿ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯನ್ನು ಸೂಚಿಸುತ್ತದೆ ಒಂದು ರಾಜ್ಯದಲ್ಲಿ .

ಸಾಮಾನ್ಯವಾಗಿ ಸಂಭವನೀಯತೆಗಳು ಪರಿಗಣನೆಯಲ್ಲಿರುವ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಅವಲಂಬಿಸಿ ಚದರ ಮ್ಯಾಟ್ರಿಕ್ಸ್ (ಸೀಮಿತ ಅಥವಾ ಎಣಿಸಬಹುದಾದ) ಆಗಿ ಸಂಯೋಜಿಸಲಾಗಿದೆ:

,

ಮತ್ತು ಮಾರ್ಕೊವ್ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಅಥವಾ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆ ಮ್ಯಾಟ್ರಿಕ್ಸ್ಮಾರ್ಕೋವ್ ಸರಣಿ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ನಲ್ಲಿ
i ಸಾಲು r.v ಯ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆಯನ್ನು ಪ್ರತಿನಿಧಿಸುತ್ತದೆ.
ಎಂದು ಒದಗಿಸಿದೆ
. ರಾಜ್ಯಗಳ ಸಂಖ್ಯೆ ಸೀಮಿತವಾಗಿದ್ದರೆ, ಆಗ - ಒಂದು ಸೀಮಿತ ಚೌಕ ಮ್ಯಾಟ್ರಿಕ್ಸ್ ಅದರ ಕ್ರಮ (ಸಾಲುಗಳ ಸಂಖ್ಯೆ) ರಾಜ್ಯಗಳ ಸಂಖ್ಯೆಗೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ಸ್ವಾಭಾವಿಕವಾಗಿ, ಸಂಭವನೀಯತೆಗಳು ಕೆಳಗಿನ ಎರಡು ಷರತ್ತುಗಳನ್ನು ಪೂರೈಸಿ:

ಎ)
,

b)
ಪ್ರತಿ ಸ್ಥಿರಕ್ಕೆ

ಸ್ಥಿತಿ ಬಿ) ಪ್ರತಿ ಪ್ರಯೋಗವು ಒಂದು ರಾಜ್ಯದಿಂದ ಮತ್ತೊಂದು ರಾಜ್ಯಕ್ಕೆ ಕೆಲವು ಪರಿವರ್ತನೆಯನ್ನು ಉಂಟುಮಾಡುತ್ತದೆ ಎಂಬ ಅಂಶವನ್ನು ಪ್ರತಿಬಿಂಬಿಸುತ್ತದೆ. ಅನುಕೂಲಕ್ಕಾಗಿ, ನಾವು ಸಾಮಾನ್ಯವಾಗಿ ಮಾತನಾಡುತ್ತೇವೆ ಪರಿವರ್ತನೆಮತ್ತು ರಾಜ್ಯವು ಬದಲಾಗದೆ ಇರುವ ಸಂದರ್ಭದಲ್ಲಿ. ಒಂದು ಸಮರ್ಥನೆ ಇದೆ.

ಪ್ರಮೇಯ 17.2.ಸಂಭವನೀಯತೆಗಳನ್ನು ನೀಡಿದರೆ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗುತ್ತದೆ(46), ಅಂದರೆ

ಮತ್ತು ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ನ ಸಂಭವನೀಯತೆಯ ವಿತರಣೆ .

ಪುರಾವೆ.ಯಾವುದೇ ಪರಿಮಿತಕ್ಕೆ ಅದನ್ನು ತೋರಿಸೋಣ ಸಂಭವನೀಯತೆಯನ್ನು ಹೇಗೆ ಲೆಕ್ಕ ಹಾಕಲಾಗುತ್ತದೆ

ಏಕೆಂದರೆ, ಒಟ್ಟು ಸಂಭವನೀಯತೆಯ ಸೂತ್ರದ ಪ್ರಕಾರ, ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳಿಗೆ ಸಂಬಂಧಿಸಿದ ಯಾವುದೇ ಇತರ ಸಂಭವನೀಯತೆಗಳನ್ನು ರೂಪದ ಪದಗಳನ್ನು (ಸದಸ್ಯರು) ಸಂಕ್ಷೇಪಿಸುವ ಮೂಲಕ ಪಡೆಯಬಹುದು (47).

ನಾವು ಹೊಂದಿರುವ ಷರತ್ತುಬದ್ಧ ಸಂಭವನೀಯತೆಯ ವ್ಯಾಖ್ಯಾನದಿಂದ

ಆದರೆ ಮಾರ್ಕೋವ್ ಪ್ರಕ್ರಿಯೆಯ ವ್ಯಾಖ್ಯಾನದಿಂದ ನಾವು ಪಡೆಯುತ್ತೇವೆ

ಸಮಾನತೆ (49) ಅನ್ನು (48) ಗೆ ಹಾಕಿದರೆ ನಾವು ಪಡೆಯುತ್ತೇವೆ

ಈ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಅನುಕ್ರಮವಾಗಿ ಮುಂದುವರಿಸಿ, ನಾವು ಪಡೆಯುತ್ತೇವೆ:

ಪ್ರಕ್ರಿಯೆಯನ್ನು ಸಂಪೂರ್ಣವಾಗಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ. ಏನು ಸಾಬೀತು ಮಾಡಬೇಕಾಗಿತ್ತು.

ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳಿಗೆ ರಷ್ಯಾದ ಅತ್ಯುತ್ತಮ ಗಣಿತಜ್ಞ ಎ.ಎ. ಮಾರ್ಕೊವ್ (1856-1922), ಅವರು ಮೊದಲು ಯಾದೃಚ್ಛಿಕ ಅಸ್ಥಿರಗಳ ಸಂಭವನೀಯ ಸಂಬಂಧದ ಅಧ್ಯಯನವನ್ನು ಪ್ರಾರಂಭಿಸಿದರು ಮತ್ತು "ಸಂಭವನೀಯ ಡೈನಾಮಿಕ್ಸ್" ಎಂದು ಕರೆಯಬಹುದಾದ ಸಿದ್ಧಾಂತವನ್ನು ರಚಿಸಿದರು. ತರುವಾಯ, ಈ ಸಿದ್ಧಾಂತದ ಅಡಿಪಾಯವು ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳ ಸಾಮಾನ್ಯ ಸಿದ್ಧಾಂತಕ್ಕೆ ಆರಂಭಿಕ ಆಧಾರವಾಯಿತು, ಹಾಗೆಯೇ ಪ್ರಸರಣ ಪ್ರಕ್ರಿಯೆಗಳ ಸಿದ್ಧಾಂತ, ವಿಶ್ವಾಸಾರ್ಹತೆಯ ಸಿದ್ಧಾಂತ, ಸರತಿ ಸಿದ್ಧಾಂತ, ಇತ್ಯಾದಿಗಳಂತಹ ಪ್ರಮುಖ ಅನ್ವಯಿಕ ವಿಜ್ಞಾನಗಳು. ಪ್ರಸ್ತುತ, ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಳ ಸಿದ್ಧಾಂತ ಮತ್ತು ಅದರ ಅನ್ವಯಗಳನ್ನು ಯಂತ್ರಶಾಸ್ತ್ರ, ಭೌತಶಾಸ್ತ್ರ, ರಸಾಯನಶಾಸ್ತ್ರ, ಇತ್ಯಾದಿ ವಿಜ್ಞಾನದ ವಿವಿಧ ಕ್ಷೇತ್ರಗಳಲ್ಲಿ ವ್ಯಾಪಕವಾಗಿ ಬಳಸಲಾಗುತ್ತದೆ.

ಗಣಿತದ ಉಪಕರಣದ ತುಲನಾತ್ಮಕ ಸರಳತೆ ಮತ್ತು ಸ್ಪಷ್ಟತೆ, ಹೆಚ್ಚಿನ ವಿಶ್ವಾಸಾರ್ಹತೆ ಮತ್ತು ಪಡೆದ ಪರಿಹಾರಗಳ ನಿಖರತೆಯಿಂದಾಗಿ, ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆಗಳು ಕಾರ್ಯಾಚರಣೆಯ ಸಂಶೋಧನೆ ಮತ್ತು ಸೂಕ್ತ ನಿರ್ಧಾರ ತೆಗೆದುಕೊಳ್ಳುವ ಸಿದ್ಧಾಂತದಲ್ಲಿ ತೊಡಗಿರುವ ತಜ್ಞರಿಂದ ವಿಶೇಷ ಗಮನವನ್ನು ಪಡೆದಿವೆ.

ಮೇಲೆ ತಿಳಿಸಿದ ಸರಳತೆ ಮತ್ತು ಸ್ಪಷ್ಟತೆಯ ಹೊರತಾಗಿಯೂ, ಮಾರ್ಕೊವ್ ಸರಪಳಿಗಳ ಸಿದ್ಧಾಂತದ ಪ್ರಾಯೋಗಿಕ ಅನ್ವಯಕ್ಕೆ ಉದಾಹರಣೆಗಳನ್ನು ಪ್ರಸ್ತುತಪಡಿಸುವ ಮೊದಲು ಚರ್ಚಿಸಬೇಕಾದ ಕೆಲವು ನಿಯಮಗಳು ಮತ್ತು ಮೂಲಭೂತ ತತ್ವಗಳ ಜ್ಞಾನದ ಅಗತ್ಯವಿರುತ್ತದೆ.

ಸೂಚಿಸಿದಂತೆ, ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳು ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳ (SP) ವಿಶೇಷ ಪ್ರಕರಣಗಳನ್ನು ಉಲ್ಲೇಖಿಸುತ್ತವೆ. ಪ್ರತಿಯಾಗಿ, ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳು ಯಾದೃಚ್ಛಿಕ ಕ್ರಿಯೆಯ (SF) ಪರಿಕಲ್ಪನೆಯನ್ನು ಆಧರಿಸಿವೆ.

ಯಾದೃಚ್ಛಿಕ ಕಾರ್ಯವು ಒಂದು ಕಾರ್ಯವಾಗಿದ್ದು, ಅದರ ಮೌಲ್ಯವು ವಾದದ ಯಾವುದೇ ಮೌಲ್ಯಕ್ಕೆ ಯಾದೃಚ್ಛಿಕ ವೇರಿಯಬಲ್ (RV) ಆಗಿದೆ. ಬೇರೆ ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ, SF ಅನ್ನು ಒಂದು ಕಾರ್ಯವೆಂದು ಕರೆಯಬಹುದು, ಅದು ಪ್ರತಿ ಪರೀಕ್ಷೆಯಲ್ಲಿ, ಕೆಲವು ಹಿಂದೆ ತಿಳಿದಿಲ್ಲದ ರೂಪವನ್ನು ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ.

SF ನ ಅಂತಹ ಉದಾಹರಣೆಗಳೆಂದರೆ: ಎಲೆಕ್ಟ್ರಿಕಲ್ ಸರ್ಕ್ಯೂಟ್‌ನಲ್ಲಿ ವೋಲ್ಟೇಜ್ ಏರಿಳಿತಗಳು, ವೇಗದ ಮಿತಿಯೊಂದಿಗೆ ರಸ್ತೆಯ ಒಂದು ವಿಭಾಗದಲ್ಲಿ ಕಾರಿನ ವೇಗ, ನಿರ್ದಿಷ್ಟ ವಿಭಾಗದಲ್ಲಿ ಒಂದು ಭಾಗದ ಮೇಲ್ಮೈ ಒರಟುತನ, ಇತ್ಯಾದಿ.

ನಿಯಮದಂತೆ, SF ನ ವಾದವು ಸಮಯವಾಗಿದ್ದರೆ, ಅಂತಹ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಯಾದೃಚ್ಛಿಕ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಎಂದು ನಂಬಲಾಗಿದೆ. ನಿರ್ಧಾರ ಸಿದ್ಧಾಂತಕ್ಕೆ ಹತ್ತಿರವಾದ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳ ಮತ್ತೊಂದು ವ್ಯಾಖ್ಯಾನವಿದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಸಮಯ ಅಥವಾ ಇತರ ವಾದಕ್ಕೆ ಸಂಬಂಧಿಸಿದಂತೆ ಯಾವುದೇ ಭೌತಿಕ ಅಥವಾ ತಾಂತ್ರಿಕ ವ್ಯವಸ್ಥೆಯ ಸ್ಥಿತಿಗಳಲ್ಲಿ ಯಾದೃಚ್ಛಿಕ ಬದಲಾವಣೆಯ ಪ್ರಕ್ರಿಯೆ ಎಂದು ಅರ್ಥೈಸಲಾಗುತ್ತದೆ.

ನೀವು ರಾಜ್ಯವನ್ನು ಗೊತ್ತುಪಡಿಸಿದರೆ ಮತ್ತು ಅವಲಂಬನೆಯನ್ನು ಚಿತ್ರಿಸಿದರೆ, ಅಂತಹ ಅವಲಂಬನೆಯು ಯಾದೃಚ್ಛಿಕ ಕಾರ್ಯವಾಗಿದೆ ಎಂದು ನೋಡುವುದು ಸುಲಭ.

ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳನ್ನು ರಾಜ್ಯಗಳ ಪ್ರಕಾರಗಳು ಮತ್ತು ಆರ್ಗ್ಯುಮೆಂಟ್ ಟಿ ಪ್ರಕಾರ ವರ್ಗೀಕರಿಸಲಾಗಿದೆ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳು ಪ್ರತ್ಯೇಕ ಅಥವಾ ನಿರಂತರ ಸ್ಥಿತಿಗಳು ಅಥವಾ ಸಮಯದೊಂದಿಗೆ ಇರಬಹುದು.

ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳ ವರ್ಗೀಕರಣದ ಮೇಲಿನ ಉದಾಹರಣೆಗಳ ಜೊತೆಗೆ, ಮತ್ತೊಂದು ಪ್ರಮುಖ ಆಸ್ತಿ ಇದೆ. ಈ ಆಸ್ತಿಯು ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಗಳ ಸ್ಥಿತಿಗಳ ನಡುವಿನ ಸಂಭವನೀಯ ಸಂಪರ್ಕವನ್ನು ವಿವರಿಸುತ್ತದೆ. ಆದ್ದರಿಂದ, ಉದಾಹರಣೆಗೆ, ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ಪ್ರತಿ ನಂತರದ ಸ್ಥಿತಿಗೆ ಸಿಸ್ಟಮ್ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯು ಹಿಂದಿನ ಸ್ಥಿತಿಯ ಮೇಲೆ ಮಾತ್ರ ಅವಲಂಬಿತವಾಗಿದ್ದರೆ, ಅಂತಹ ಪ್ರಕ್ರಿಯೆಯನ್ನು ನಂತರದ ಪರಿಣಾಮವಿಲ್ಲದ ಪ್ರಕ್ರಿಯೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ನಾವು ಗಮನಿಸೋಣ, ಮೊದಲನೆಯದಾಗಿ, ಪ್ರತ್ಯೇಕ ರಾಜ್ಯಗಳು ಮತ್ತು ಸಮಯವನ್ನು ಹೊಂದಿರುವ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯನ್ನು ಯಾದೃಚ್ಛಿಕ ಅನುಕ್ರಮ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಯಾದೃಚ್ಛಿಕ ಅನುಕ್ರಮವು ಮಾರ್ಕೊವ್ ಆಸ್ತಿಯನ್ನು ಹೊಂದಿದ್ದರೆ, ಅದನ್ನು ಮಾರ್ಕೊವ್ ಚೈನ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಮತ್ತೊಂದೆಡೆ, ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯಲ್ಲಿ ರಾಜ್ಯಗಳು ಪ್ರತ್ಯೇಕವಾಗಿದ್ದರೆ, ಸಮಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ ಮತ್ತು ನಂತರದ ಪರಿಣಾಮದ ಆಸ್ತಿಯನ್ನು ಸಂರಕ್ಷಿಸಲಾಗಿದೆ, ನಂತರ ಅಂತಹ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯನ್ನು ನಿರಂತರ ಸಮಯದೊಂದಿಗೆ ಮಾರ್ಕೊವ್ ಪ್ರಕ್ರಿಯೆ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಮಾರ್ಕೊವ್ ಯಾದೃಚ್ಛಿಕ ಪ್ರಕ್ರಿಯೆಯು ಪ್ರಕ್ರಿಯೆಯ ಸಮಯದಲ್ಲಿ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಗಳು ಸ್ಥಿರವಾಗಿದ್ದರೆ ಏಕರೂಪವಾಗಿರುತ್ತದೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ.

ಎರಡು ಷರತ್ತುಗಳನ್ನು ನೀಡಿದರೆ ಮಾರ್ಕೊವ್ ಸರಪಳಿಯನ್ನು ನೀಡಲಾಗಿದೆ ಎಂದು ಪರಿಗಣಿಸಲಾಗುತ್ತದೆ.

1. ಮ್ಯಾಟ್ರಿಕ್ಸ್ ರೂಪದಲ್ಲಿ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಗಳ ಒಂದು ಸೆಟ್ ಇದೆ:

2. ಆರಂಭಿಕ ಸಂಭವನೀಯತೆಗಳ ವೆಕ್ಟರ್ ಇದೆ

ವ್ಯವಸ್ಥೆಯ ಆರಂಭಿಕ ಸ್ಥಿತಿಯನ್ನು ವಿವರಿಸುತ್ತದೆ.

ಮ್ಯಾಟ್ರಿಕ್ಸ್ ರೂಪದ ಜೊತೆಗೆ, ಮಾರ್ಕೊವ್ ಚೈನ್ ಮಾದರಿಯನ್ನು ನಿರ್ದೇಶಿಸಿದ ತೂಕದ ಗ್ರಾಫ್ (Fig. 1) ಎಂದು ಪ್ರತಿನಿಧಿಸಬಹುದು.

ಅಕ್ಕಿ. 1

ಮಾರ್ಕೊವ್ ಚೈನ್ ಸಿಸ್ಟಮ್ನ ರಾಜ್ಯಗಳ ಗುಂಪನ್ನು ಒಂದು ನಿರ್ದಿಷ್ಟ ರೀತಿಯಲ್ಲಿ ವರ್ಗೀಕರಿಸಲಾಗಿದೆ, ಸಿಸ್ಟಮ್ನ ಮುಂದಿನ ನಡವಳಿಕೆಯನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಳ್ಳುತ್ತದೆ.

1. ಬದಲಾಯಿಸಲಾಗದ ಸೆಟ್ (ಚಿತ್ರ 2).

ಚಿತ್ರ.2.

ಹಿಂತಿರುಗಿಸದ ಗುಂಪಿನ ಸಂದರ್ಭದಲ್ಲಿ, ಈ ಗುಂಪಿನೊಳಗೆ ಯಾವುದೇ ಪರಿವರ್ತನೆಗಳು ಸಾಧ್ಯ. ಸಿಸ್ಟಮ್ ಈ ಸೆಟ್ ಅನ್ನು ಬಿಡಬಹುದು, ಆದರೆ ಅದಕ್ಕೆ ಹಿಂತಿರುಗಲು ಸಾಧ್ಯವಿಲ್ಲ.

2. ರಿಟರ್ನ್ ಸೆಟ್ (ಚಿತ್ರ 3).

ಅಕ್ಕಿ. 3.

ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಸೆಟ್ನಲ್ಲಿ ಯಾವುದೇ ಪರಿವರ್ತನೆಗಳು ಸಹ ಸಾಧ್ಯವಿದೆ. ಸಿಸ್ಟಮ್ ಈ ಸೆಟ್ ಅನ್ನು ನಮೂದಿಸಬಹುದು, ಆದರೆ ಅದನ್ನು ಬಿಡಲು ಸಾಧ್ಯವಿಲ್ಲ.

3. ಎರ್ಗೋಡಿಕ್ ಸೆಟ್ (ಚಿತ್ರ 4).

ಅಕ್ಕಿ. 4.

ಎರ್ಗೋಡಿಕ್ ಸೆಟ್‌ನ ಸಂದರ್ಭದಲ್ಲಿ, ಸೆಟ್‌ನೊಳಗೆ ಯಾವುದೇ ಪರಿವರ್ತನೆಗಳು ಸಾಧ್ಯ, ಆದರೆ ಸೆಟ್‌ನಿಂದ ಮತ್ತು ಸೆಟ್‌ಗೆ ಪರಿವರ್ತನೆಗಳನ್ನು ಹೊರಗಿಡಲಾಗುತ್ತದೆ.

4. ಹೀರಿಕೊಳ್ಳುವ ಸೆಟ್ (ಚಿತ್ರ 5)

ಅಕ್ಕಿ. 5.

ಸಿಸ್ಟಮ್ ಈ ಸೆಟ್ ಅನ್ನು ಪ್ರವೇಶಿಸಿದಾಗ, ಪ್ರಕ್ರಿಯೆಯು ಕೊನೆಗೊಳ್ಳುತ್ತದೆ.

ಕೆಲವು ಸಂದರ್ಭಗಳಲ್ಲಿ, ಪ್ರಕ್ರಿಯೆಯ ಯಾದೃಚ್ಛಿಕತೆಯ ಹೊರತಾಗಿಯೂ, ವಿತರಣಾ ಕಾನೂನುಗಳು ಅಥವಾ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಯ ನಿಯತಾಂಕಗಳನ್ನು ಸ್ವಲ್ಪ ಮಟ್ಟಿಗೆ ನಿಯಂತ್ರಿಸಲು ಸಾಧ್ಯವಿದೆ. ಅಂತಹ ಮಾರ್ಕೋವ್ ಸರಪಳಿಗಳನ್ನು ನಿಯಂತ್ರಿತ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ನಿಸ್ಸಂಶಯವಾಗಿ, ನಿಯಂತ್ರಿತ ಮಾರ್ಕೊವ್ ಸರಪಳಿಗಳ (CMC) ಸಹಾಯದಿಂದ, ನಿರ್ಧಾರ ತೆಗೆದುಕೊಳ್ಳುವ ಪ್ರಕ್ರಿಯೆಯು ವಿಶೇಷವಾಗಿ ಪರಿಣಾಮಕಾರಿಯಾಗುತ್ತದೆ, ನಂತರ ಚರ್ಚಿಸಲಾಗುವುದು.

ಡಿಸ್ಕ್ರೀಟ್ ಮಾರ್ಕೊವ್ ಚೈನ್ (DMC) ನ ಮುಖ್ಯ ಲಕ್ಷಣವೆಂದರೆ ಪ್ರಕ್ರಿಯೆಯ ಪ್ರತ್ಯೇಕ ಹಂತಗಳ (ಹಂತಗಳು) ನಡುವಿನ ಸಮಯದ ಮಧ್ಯಂತರಗಳ ನಿರ್ಣಯ. ಆದಾಗ್ಯೂ, ಸಾಮಾನ್ಯವಾಗಿ ನೈಜ ಪ್ರಕ್ರಿಯೆಗಳಲ್ಲಿ ಈ ಆಸ್ತಿಯನ್ನು ಗಮನಿಸಲಾಗುವುದಿಲ್ಲ ಮತ್ತು ಮಧ್ಯಂತರಗಳು ಕೆಲವು ವಿತರಣಾ ಕಾನೂನಿನೊಂದಿಗೆ ಯಾದೃಚ್ಛಿಕವಾಗಿ ಹೊರಹೊಮ್ಮುತ್ತವೆ, ಆದಾಗ್ಯೂ ಪ್ರಕ್ರಿಯೆಯ ಮಾರ್ಕೊವ್ ಆಸ್ತಿಯನ್ನು ಸಂರಕ್ಷಿಸಲಾಗಿದೆ. ಅಂತಹ ಯಾದೃಚ್ಛಿಕ ಅನುಕ್ರಮಗಳನ್ನು ಅರೆ-ಮಾರ್ಕೊವ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಹೆಚ್ಚುವರಿಯಾಗಿ, ಮೇಲೆ ತಿಳಿಸಲಾದ ಕೆಲವು ರಾಜ್ಯಗಳ ಉಪಸ್ಥಿತಿ ಮತ್ತು ಅನುಪಸ್ಥಿತಿಯನ್ನು ಗಣನೆಗೆ ತೆಗೆದುಕೊಂಡು, ಮಾರ್ಕೊವ್ ಸರಪಳಿಗಳು ಕನಿಷ್ಠ ಒಂದು ಹೀರಿಕೊಳ್ಳುವ ಸ್ಥಿತಿ ಇದ್ದರೆ ಹೀರಿಕೊಳ್ಳಬಹುದು ಅಥವಾ ಪರಿವರ್ತನೆಯ ಸಂಭವನೀಯತೆಗಳು ಎರ್ಗೋಡಿಕ್ ಸೆಟ್ ಅನ್ನು ರೂಪಿಸಿದರೆ ಎರ್ಗೋಡಿಕ್ ಆಗಿರಬಹುದು. ಪ್ರತಿಯಾಗಿ, ಎರ್ಗೋಡಿಕ್ ಸರಪಳಿಗಳು ನಿಯಮಿತ ಅಥವಾ ಆವರ್ತಕವಾಗಿರಬಹುದು. ಆವರ್ತಕ ಸರಪಳಿಗಳು ನಿಯಮಿತವಾದವುಗಳಿಂದ ಭಿನ್ನವಾಗಿರುತ್ತವೆ, ನಿರ್ದಿಷ್ಟ ಸಂಖ್ಯೆಯ ಹಂತಗಳ ಮೂಲಕ ಪರಿವರ್ತನೆಯ ಸಮಯದಲ್ಲಿ (ಚಕ್ರಗಳು) ಕೆಲವು ಸ್ಥಿತಿಗೆ ಹಿಂತಿರುಗುವುದು ಸಂಭವಿಸುತ್ತದೆ. ನಿಯಮಿತ ಸರಪಳಿಗಳು ಈ ಆಸ್ತಿಯನ್ನು ಹೊಂದಿಲ್ಲ.