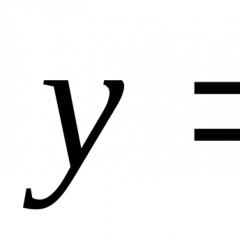ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳ ಒಮ್ಮುಖದ ಪರೀಕ್ಷೆಗಳು. ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಹೇಗೆ ಲೆಕ್ಕ ಹಾಕುವುದು ಮತ್ತು ಅದರ ಒಮ್ಮುಖವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಹೇಗೆ. ವ್ಯಾಖ್ಯಾನ ಮತ್ತು ಮೂಲ ಗುಣಲಕ್ಷಣಗಳು

ಪ್ರಮೇಯ 12.11 (ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳ ಹೋಲಿಕೆಗಾಗಿ ಪರೀಕ್ಷೆ). f(x) ಮತ್ತು g(x) ಕಾರ್ಯಗಳು ಮಧ್ಯಂತರದಲ್ಲಿ [a, ">) ನಿರಂತರವಾಗಿರಲಿ ಮತ್ತು ಅದರ ಮೇಲೆ 0 ಫಿಕ್ಸ್) ?(x) ಷರತ್ತನ್ನು ಪೂರೈಸಲಿ. ನಂತರ ಸಮಗ್ರತೆಯ ಒಮ್ಮುಖದಿಂದ

ಅವಿಭಾಜ್ಯ ಒಮ್ಮುಖವಾಗುತ್ತದೆ

ಮತ್ತು ಪ್ರತಿಕ್ರಮದಲ್ಲಿ, ಅವಿಭಾಜ್ಯ (12.64) ದ ಡೈವರ್ಜೆನ್ಸ್‌ನಿಂದ ಅವಿಭಾಜ್ಯ (12.63) ಅನ್ನು ಅನುಸರಿಸುತ್ತದೆ.

ಪುರಾವೆ.ನಾವು ಈ ಕೆಳಗಿನ ಸಂಕೇತವನ್ನು ಪರಿಚಯಿಸೋಣ:

ಕಾರ್ಯ ಪಿ(ಕೆ)ಕಡಿಮೆಯಾಗುವುದಿಲ್ಲ; ವಾಸ್ತವವಾಗಿ, ವೇಳೆ ಮತ್ತು ನಾನು 2, ನಂತರ

ಜೆ ಸರಿಪಡಿಸಿ) dx>0, ಮತ್ತು ನಂತರ

ಮೌಲ್ಯಗಳ ಅನುಕ್ರಮವನ್ನು ತೆಗೆದುಕೊಳ್ಳೋಣ (/?„) -> ">; ನಂತರ ಕಾರ್ಯ ಮೌಲ್ಯಗಳ ಅನುಗುಣವಾದ ಅನುಕ್ರಮ (F(Rn))ಏಕತಾನತೆ ಮತ್ತು ಕಡಿಮೆಯಾಗುವುದಿಲ್ಲ. ಅವಿಭಾಜ್ಯ (12.63) ಒಮ್ಮುಖವಾಗಲಿ, ನಂತರ ಅನುಕ್ರಮ (67 (67) ಆರ್ಇದು)) ಸೀಮಿತವಾಗಿದೆ; ಆದರೆ ನಂತರ ಅನುಕ್ರಮವೂ ಸೀಮಿತವಾಗಿರುತ್ತದೆ (ಎಫ್(/?„)), ಅಂದರೆ ಪ್ರಮೇಯ 7.13 ಮೂಲಕ ಅದು ಒಮ್ಮುಖವಾಗುತ್ತದೆ. ಆದ್ದರಿಂದ ಒಂದು ಮಿತಿ ಇದೆ F(R)ನಲ್ಲಿ ಆರ್-+ «>, ಅಂದರೆ. ಅವಿಭಾಜ್ಯ (12.64) ಒಮ್ಮುಖವಾಗುತ್ತದೆ.

ಈಗ ಪ್ರಮೇಯದ ಎರಡನೇ ಭಾಗವನ್ನು ಸಾಬೀತುಪಡಿಸೋಣ; ಅವಿಭಾಜ್ಯ (12.64) ಭಿನ್ನವಾಗಿರಲಿ. ಅವಿಭಾಜ್ಯ (12.63) ಒಮ್ಮುಖವಾಗುತ್ತದೆ ಎಂದು ನಾವು ಭಾವಿಸಿದರೆ, ಮೇಲೆ ಸಾಬೀತುಪಡಿಸಿದ ಪ್ರಕಾರ, ಅವಿಭಾಜ್ಯ (12.64) ಸಹ ಒಮ್ಮುಖವಾಗಬೇಕು, ಇದು ಸ್ಥಿತಿಗೆ ವಿರುದ್ಧವಾಗಿದೆ. ಪ್ರಮೇಯವು ಸಾಬೀತಾಗಿದೆ. ?

ಕಾಮೆಂಟ್ ಮಾಡಿ.ಇದೇ ರೀತಿಯ ಹೋಲಿಕೆ ಮಾನದಂಡವು ಎರಡನೇ ವಿಧದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಸಹ ಮಾನ್ಯವಾಗಿದೆ. ಕಾರ್ಯಗಳು /(x) ಮತ್ತು ಜಿ (X)ಅರ್ಧ ಮಧ್ಯಂತರದಲ್ಲಿ ನಿರಂತರ [a>b)ಮತ್ತು ಏಕ ಬಿಂದುವಿನ ಕೆಲವು ನೆರೆಹೊರೆಯಲ್ಲಿರುವ ಎಲ್ಲಾ ಬಿಂದುಗಳಿಗೆ ಬಿಪೂರ್ಣಗೊಂಡಿದೆ

ಷರತ್ತುಗಳು 0 (x), ನಂತರ ಅವಿಭಾಜ್ಯ Jg(x)dx ನ ಒಮ್ಮುಖದಿಂದ ಅದು ಅನುಸರಿಸುತ್ತದೆ

ಅವಿಭಾಜ್ಯ J/(x)dx ನ ಭಿನ್ನತೆ, ಮತ್ತು ಅವಿಭಾಜ್ಯ J/(x)dx ನ ವ್ಯತ್ಯಾಸದಿಂದ -

ಅವಿಭಾಜ್ಯ Jg(x)dx ನ ಶಕ್ತಿ.

ಅನುಚಿತ ಅವಿಭಾಜ್ಯಗಳ ಒಮ್ಮುಖವನ್ನು ಅಧ್ಯಯನ ಮಾಡಲು ಉದಾಹರಣೆಗಳನ್ನು ಪರಿಗಣಿಸೋಣ.

ಉದಾಹರಣೆ 27. ಟಿ. ^-.

X 3 (1 + e L)

ಪರಿಹಾರ.ಈ ಅವಿಭಾಜ್ಯದಲ್ಲಿನ ಇಂಟಿಗ್ರಾಂಡ್ ಅನ್ನು ಫಂಕ್ಷನ್‌ನೊಂದಿಗೆ ಹೋಲಿಸೋಣ

Dg. ಇದು ಸ್ಪಷ್ಟವಾಗಿದೆ -ಆರ್-

X g* (1+0 x J

gral J-jdx ಒಮ್ಮುಖವಾಗುತ್ತದೆ; ಆದ್ದರಿಂದ, ಹೋಲಿಕೆ ಮಾನದಂಡದ ಪ್ರಕಾರ, ನೀಡಲಾಗಿದೆ 1 X

ನಾಲ್ ಅವಿಭಾಜ್ಯ.

ಉದಾಹರಣೆ 28. I-.

ಪರಿಹಾರ.ಈ ಅವಿಭಾಜ್ಯತೆಯ ಇಂಟಿಗ್ರ್ಯಾಂಡ್ ಅನ್ನು 1/x ಕಾರ್ಯದೊಂದಿಗೆ ಹೋಲಿಸುವುದು,

ಮಧ್ಯಂತರ 1 ರಂದು (1 + x ನಲ್ಲಿ)/x > 1/x ಎಂದು ನಾವು ನೋಡುತ್ತೇವೆ

ವೈವಿಧ್ಯಗೊಳಿಸುತ್ತದೆ, ಆದ್ದರಿಂದ, ಹೋಲಿಕೆಯಿಂದ, ಈ ಅವಿಭಾಜ್ಯವು ಸಹ ಭಿನ್ನವಾಗಿರುತ್ತದೆ.

ಕೊನೆಯಲ್ಲಿ, ಮೊದಲ ವಿಧದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಒಮ್ಮುಖವಾಗಿಸುವ ಕೌಚಿ ಮಾನದಂಡವನ್ನು ನಾವು ಪುರಾವೆಗಳಿಲ್ಲದೆ ಪ್ರಸ್ತುತಪಡಿಸುತ್ತೇವೆ.

12.10.4. ಅನುಚಿತ ಅವಿಭಾಜ್ಯಗಳ ಸಂಪೂರ್ಣ ಮತ್ತು ಷರತ್ತುಬದ್ಧ ಒಮ್ಮುಖ

ವ್ಯಾಖ್ಯಾನ 5. ಅನುಚಿತ ಅವಿಭಾಜ್ಯ J/(x)dx ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಸಂಪೂರ್ಣವಾಗಿ

ಒಮ್ಮುಖ, ಅವಿಭಾಜ್ಯ J|/(x)|dx ಒಮ್ಮುಖವಾಗಿದ್ದರೆ.

ವ್ಯಾಖ್ಯಾನ 6. ಅನುಚಿತ ಅವಿಭಾಜ್ಯ J /(x) dx ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಷರತ್ತುಬದ್ಧವಾಗಿ ಹೋಲುತ್ತದೆ

ಶಾಶ್ವತ, ಅದು ಒಮ್ಮುಖವಾಗಿದ್ದರೆ ಮತ್ತು ಅವಿಭಾಜ್ಯ J|/(x)|dx ಭಿನ್ನವಾಗಿದ್ದರೆ.

ಸಮಗ್ರತೆಯ ಸಂಪೂರ್ಣ ಒಮ್ಮುಖವು ಅಂದಾಜು 3 ರ ಕಾರಣದಿಂದಾಗಿ ಅದರ ಒಮ್ಮುಖವನ್ನು ಸೂಚಿಸುತ್ತದೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ ನಿರ್ದಿಷ್ಟ ಅವಿಭಾಜ್ಯಮತ್ತು ಕೌಚಿ ಮಾನದಂಡ.

ಪ್ರಮೇಯ 12.13 (ಡಿರಿಚ್ಲೆಟ್-ಅಬೆಲ್ ಪರೀಕ್ಷೆ*). ಕಾರ್ಯವು /(x) ನಿರಂತರವಾಗಿರಲಿ ಮತ್ತು ಬೌಂಡೆಡ್ ಆಂಟಿಡೆರಿವೇಟಿವ್ ಅನ್ನು ಹೊಂದಿರಲಿ ಎಫ್(x) ಮಧ್ಯಂತರದಲ್ಲಿ [a, «>], ಮತ್ತು ಫಂಕ್ಷನ್ g(x) ಈ ಮಧ್ಯಂತರದಲ್ಲಿ ನಿರಂತರ ವ್ಯುತ್ಪನ್ನವನ್ನು ಹೊಂದಿದೆ, ಹೆಚ್ಚಾಗುವುದಿಲ್ಲ ಮತ್ತು x -> ©o ನಂತೆ ಶೂನ್ಯಕ್ಕೆ ಒಲವು ತೋರುತ್ತದೆ. ನಂತರ ಅನುಚಿತ ಅವಿಭಾಜ್ಯ

ಒಮ್ಮುಖವಾಗುತ್ತದೆ.

ಪುರಾವೆ.ಅವಿಭಾಜ್ಯ J /(x)g(x)dx ಗೆ ಭಾಗಗಳ ಮೂಲಕ ಏಕೀಕರಣವನ್ನು ಅನ್ವಯಿಸೋಣ

ಅನಿಯಂತ್ರಿತ ವಿಭಾಗದಲ್ಲಿ ಆರ್ ಆರ್"ಇದರೊಂದಿಗೆ [ ಎ, ° °). ನಾವು ಹೊಂದಿದ್ದೇವೆ:

ಪ್ರಮೇಯ 12.12. ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯ (12.64) ಒಮ್ಮುಖವಾಗಲು, ಯಾವುದೇ e > 0 ಗೆ ಅಂತಹ ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಅವಶ್ಯಕ ಮತ್ತು ಸಾಕಾಗುತ್ತದೆ ಎ> 0, ಯಾವುದಾದರೂ ಆರ್"ಮತ್ತು /?", ಹೆಚ್ಚು ಎ,ಅಸಮಾನತೆ ಹೊಂದಿದೆ:

ಪ್ರಮೇಯದ ಪರಿಸ್ಥಿತಿಗಳ ಪ್ರಕಾರ F(x)ಸೀಮಿತ, ಅಂದರೆ. |F(x)| K. g(x) ಕಾರ್ಯವು ಹೆಚ್ಚಾಗುವುದಿಲ್ಲ ಮತ್ತು x -" "> ನಂತೆ ಶೂನ್ಯಕ್ಕೆ ಒಲವು ತೋರುತ್ತದೆ, ಇದರರ್ಥ. g(x)> 0, a g"(x)

ಅಬೆಲ್ ನೀಲ್ಸ್ ಹೆನ್ರಿಕ್ (1802-1829) - ನಾರ್ವೇಜಿಯನ್ ಗಣಿತಜ್ಞ.

ಪ್ರಮೇಯದ ಪರಿಸ್ಥಿತಿಗಳ ಪ್ರಕಾರ, x -> ©° ಗೆ g(x) -» 0, ಅನಿಯಂತ್ರಿತ ಸಂಖ್ಯೆಗೆ ಇ > 0 ನಾವು ಸಂಖ್ಯೆಯನ್ನು ಕಂಡುಹಿಡಿಯಬಹುದು ಎ>ಅಂತಹ ಯಾವಾಗ ಆರ್"> ಎಲ್ಅಸಮಾನತೆ ತೃಪ್ತಿಯಾಗುತ್ತದೆ g(R") ಇದನ್ನು ಅಂದಾಜು (12.68) ಗೆ ಬದಲಿಸಿ, ನಾವು ಪಡೆಯುತ್ತೇವೆ:

ಇದು ಅವಿಭಾಜ್ಯ (12.66) ಒಮ್ಮುಖಕ್ಕೆ ಕೌಚಿ ಮಾನದಂಡಕ್ಕೆ ಅನುರೂಪವಾಗಿದೆ. ಪ್ರಮೇಯವು ಸಾಬೀತಾಗಿದೆ. ?

ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳ ಒಮ್ಮುಖಕ್ಕಾಗಿ ಡಿರಿಚ್ಲೆಟ್-ಅಬೆಲ್ ಪರೀಕ್ಷೆಯನ್ನು ಬಳಸುವ ಉದಾಹರಣೆಗಳನ್ನು ಪರಿಗಣಿಸೋಣ.

ಉದಾಹರಣೆ 29. f^^dx, a>0.

ಪರಿಹಾರ./(x) = sin x ಎಂದು ಇಡೋಣ, g(x)= l/x"; ಪ್ರಮೇಯದ ಎಲ್ಲಾ ಷರತ್ತುಗಳನ್ನು ಪೂರೈಸಲಾಗಿದೆಯೇ ಎಂದು ಪರಿಶೀಲಿಸುವುದು ಸುಲಭ, ಅಂದರೆ, ಈ ಅವಿಭಾಜ್ಯವು ಒಮ್ಮುಖವಾಗುತ್ತದೆ. ಒಂದು > 1 ಗಾಗಿ, ಈ ಅವಿಭಾಜ್ಯ

ರಾಲ್ ಸಂಪೂರ್ಣವಾಗಿ ಒಮ್ಮುಖವಾಗುತ್ತದೆ. ನಿಜವಾಗಿ, |ಪಾಪ x/xP 1/d L, ಅವಿಭಾಜ್ಯ J(l/x e)dx

ಒಮ್ಮುಖವಾಗುತ್ತದೆ, ಅಂದರೆ. ಹೋಲಿಕೆ ಮಾನದಂಡದ ಮೂಲಕ (ಪ್ರಮೇಯ 12.11), ಈ ಅವಿಭಾಜ್ಯವು ಸಹ ಸಂಪೂರ್ಣವಾಗಿ ಒಮ್ಮುಖವಾಗುತ್ತದೆ.

ಉದಾಹರಣೆ 30. Jsin x 2 dx - ಫ್ರೆಸ್ನೆಲ್ ಇಂಟಿಗ್ರಲ್, o

ಪರಿಹಾರ.ಈ ಅವಿಭಾಜ್ಯವನ್ನು ಮೊತ್ತವಾಗಿ ಪ್ರತಿನಿಧಿಸೋಣ:

ಪಾಪ x 2 ರಿಂದ - ನಿರಂತರ ಕಾರ್ಯಮಧ್ಯಂತರದಲ್ಲಿ (0, 1J, (12.69) ರಲ್ಲಿ ಮೊದಲ ಅವಿಭಾಜ್ಯವು ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ. (12.69) ಬಲಭಾಗದಲ್ಲಿ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯ ಒಮ್ಮುಖವನ್ನು ನಿರ್ಧರಿಸಲು, ನಾವು /(x) = x sin x 2, ಜಿ(x) = 1/x. ನಂತರ ಕಾರ್ಯಕ್ಕಾಗಿ /(x) ಆಂಟಿಡೆರಿವೇಟಿವ್ F(x) = -cosx 2 /!ಮಧ್ಯಂತರ |1, ">) ಮೇಲೆ ಸೀಮಿತವಾಗಿದೆ, ಮತ್ತು #(x) ಧನಾತ್ಮಕವಾಗಿರುತ್ತದೆ, x -" °° ನಂತೆ ಸೊನ್ನೆಗೆ ಒಲವು ತೋರುತ್ತದೆ ಮತ್ತು (1, ©о) ನಲ್ಲಿ ನಿರಂತರ ವ್ಯುತ್ಪನ್ನವನ್ನು ಹೊಂದಿರುತ್ತದೆ. ಇದರರ್ಥ ಡಿರಿಚ್ಲೆಟ್-ಅಬೆಲ್ ಮಾನದಂಡದ ಪ್ರಕಾರ, (12.69) ರಲ್ಲಿ ಎರಡನೇ ಅವಿಭಾಜ್ಯವು ಒಮ್ಮುಖವಾಗುತ್ತದೆ, ಅಂದರೆ. ಫ್ರೆಸ್ನೆಲ್ ಇಂಟಿಗ್ರಲ್ ಕೂಡ ಒಮ್ಮುಖವಾಗುತ್ತದೆ.

ನಿಮಗೆ ತಿಳಿದಿರುವಂತೆ, ಅವಿಭಾಜ್ಯವನ್ನು ಕಂಡುಹಿಡಿಯುವುದು ಕಷ್ಟಕರವಾದ ಕೆಲಸವಾಗಿದೆ. ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಪ್ರಾರಂಭಿಸುವುದು ಮತ್ತು ಅದು ಬೇರೆಡೆಗೆ ಹೋಗುವ ಮಾರ್ಗದ ಕೊನೆಯಲ್ಲಿ ಕಂಡುಹಿಡಿಯುವುದು ದೊಡ್ಡ ನಿರಾಶೆಯಾಗಿದೆ. ಆದ್ದರಿಂದ, ಆಸಕ್ತಿಯು ಒಂದು ವಿಧದ ಕಾರ್ಯವನ್ನು ಆಧರಿಸಿ ಗಂಭೀರ ಲೆಕ್ಕಾಚಾರಗಳಿಲ್ಲದೆ, ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯತೆಯ ಒಮ್ಮುಖ ಅಥವಾ ಭಿನ್ನತೆಯ ಬಗ್ಗೆ ತೀರ್ಮಾನವನ್ನು ತೆಗೆದುಕೊಳ್ಳಲು ಅನುಮತಿಸುವ ವಿಧಾನಗಳಾಗಿವೆ. ಮೊದಲ ಮತ್ತು ಎರಡನೆಯ ಹೋಲಿಕೆ ಪ್ರಮೇಯಗಳನ್ನು ಕೆಳಗೆ ಚರ್ಚಿಸಲಾಗುವುದು, ಒಮ್ಮುಖವಾಗಲು ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡಲು ಹೆಚ್ಚು ಸಹಾಯ ಮಾಡುತ್ತದೆ.

f(x)?0 ಅನ್ನು ಅನುಮತಿಸಿ. ನಂತರ ಕಾರ್ಯಗಳು

t ಅಥವಾ -g ವೇರಿಯೇಬಲ್‌ಗಳಲ್ಲಿ ಏಕತಾನತೆಯಿಂದ ಹೆಚ್ಚುತ್ತಿದೆ (ನಾವು g>0 ಅನ್ನು ತೆಗೆದುಕೊಳ್ಳುವುದರಿಂದ, -g ಎಡದಿಂದ ಶೂನ್ಯಕ್ಕೆ ಒಲವು ತೋರುತ್ತದೆ). ವಾದಗಳು ಹೆಚ್ಚಾದಂತೆ, F 1 (t) ಮತ್ತು F 2 (-d) ಕಾರ್ಯಗಳು ಮೇಲಿನಿಂದ ಸೀಮಿತವಾಗಿದ್ದರೆ, ಇದರರ್ಥ ಅನುಗುಣವಾದ ಅನುಚಿತ ಅವಿಭಾಜ್ಯಗಳು ಒಮ್ಮುಖವಾಗುತ್ತವೆ. ಇದು ಋಣಾತ್ಮಕವಲ್ಲದ ಕಾರ್ಯಗಳ ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಮೊದಲ ಹೋಲಿಕೆ ಪ್ರಮೇಯದ ಆಧಾರವಾಗಿದೆ.

x?a ನಲ್ಲಿ f(x) ಮತ್ತು g(x) ಕಾರ್ಯಗಳು ಈ ಕೆಳಗಿನ ಷರತ್ತುಗಳನ್ನು ಪೂರೈಸಲಿ:

• 1) 0?f(x)?g(x);
• 2) f(x) ಮತ್ತು g(x) ಕಾರ್ಯಗಳು ನಿರಂತರವಾಗಿರುತ್ತವೆ.

ನಂತರ ಸಮಗ್ರತೆಯ ಒಮ್ಮುಖದಿಂದ ಅವಿಭಾಜ್ಯ ಒಮ್ಮುಖವನ್ನು ಅನುಸರಿಸುತ್ತದೆ, ಮತ್ತು ಅವಿಭಾಜ್ಯದಿಂದ ಭಿನ್ನಾಭಿಪ್ರಾಯವನ್ನು ಅನುಸರಿಸುತ್ತದೆ

0?f(x)?g(x) ಮತ್ತು ಕಾರ್ಯಗಳು ನಿರಂತರವಾಗಿರುವುದರಿಂದ, ನಂತರ

ಷರತ್ತಿನ ಮೂಲಕ, ಅವಿಭಾಜ್ಯ ಒಮ್ಮುಖವಾಗುತ್ತದೆ, ಅಂದರೆ. ಸೀಮಿತ ಮೌಲ್ಯವನ್ನು ಹೊಂದಿದೆ. ಆದ್ದರಿಂದ, ಅವಿಭಾಜ್ಯ ಕೂಡ ಒಮ್ಮುಖವಾಗುತ್ತದೆ.

ಈಗ ಅವಿಭಾಜ್ಯವನ್ನು ಬೇರೆಡೆಗೆ ಬಿಡಿ. ಅವಿಭಾಜ್ಯವು ಒಮ್ಮುಖವಾಗುತ್ತದೆ ಎಂದು ನಾವು ಭಾವಿಸೋಣ, ಆದರೆ ನಂತರ ಅವಿಭಾಜ್ಯವು ಒಮ್ಮುಖವಾಗಬೇಕು, ಇದು ಸ್ಥಿತಿಗೆ ವಿರುದ್ಧವಾಗಿದೆ. ನಮ್ಮ ಊಹೆಯು ತಪ್ಪಾಗಿದೆ, ಅವಿಭಾಜ್ಯವು ಭಿನ್ನವಾಗಿರುತ್ತದೆ.

2 ನೇ ವಿಧದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಹೋಲಿಕೆ ಪ್ರಮೇಯ.

ಮಧ್ಯಂತರದಲ್ಲಿ f(x) ಮತ್ತು g(x) ಕಾರ್ಯಗಳಿಗಾಗಿ x>+0 ಗೆ ಮಿತಿಯಿಲ್ಲದೆ ಹೆಚ್ಚಿಸಿ. x>+0 ಗಾಗಿ, ಕೆಳಗಿನ ಅಸಮಾನತೆಯು ಹೊಂದಿದೆ:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.

1 ನೇ ವಿಧದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಹೋಲಿಕೆ ಪ್ರಮೇಯ.

f(x) ಮತ್ತು g(x) ಕಾರ್ಯವು ಮಧ್ಯಂತರದಲ್ಲಿರಲಿ , ಮತ್ತು ಏಕೀಕರಣ ವಿಭಾಗವು ಸೀಮಿತವಾಗಿದೆ, ಅಂದರೆ, ಸಂಖ್ಯೆಗಳಿಂದ ಸೀಮಿತವಾಗಿದೆ ಮತ್ತು ಅನಂತದಿಂದಲ್ಲ. ಕೆಲವು ಕಾರ್ಯಗಳು ಈ ನಿರ್ಬಂಧಗಳನ್ನು ತ್ಯಜಿಸುವ ಅಗತ್ಯಕ್ಕೆ ಕಾರಣವಾಗುತ್ತವೆ. ಅನುಚಿತ ಅವಿಭಾಜ್ಯಗಳು ಹೇಗೆ ಕಾಣಿಸಿಕೊಳ್ಳುತ್ತವೆ.

ಅಸಮರ್ಪಕ ಸಮಗ್ರತೆಯ ಜ್ಯಾಮಿತೀಯ ಅರ್ಥಇದು ಸರಳವಾಗಿ ಹೊರಹೊಮ್ಮುತ್ತದೆ. ಒಂದು ಕಾರ್ಯದ ಗ್ರಾಫ್ ಆಗಿರುವ ಸಂದರ್ಭದಲ್ಲಿ ವೈ = f(X) ಅಕ್ಷದ ಮೇಲಿರುತ್ತದೆ ಎತ್ತು, ನಿರ್ದಿಷ್ಟ ಅವಿಭಾಜ್ಯವು ವಕ್ರರೇಖೆಯಿಂದ ಸುತ್ತುವರಿದ ಕರ್ವಿಲಿನಿಯರ್ ಟ್ರೆಪೆಜಾಯಿಡ್ನ ಪ್ರದೇಶವನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತದೆ ವೈ = f(X) , x-ಅಕ್ಷ ಮತ್ತು ಆರ್ಡಿನೇಟ್‌ಗಳು X = ಎ , X = ಬಿ. ಪ್ರತಿಯಾಗಿ, ಅನುಚಿತ ಅವಿಭಾಜ್ಯವು ರೇಖೆಗಳ ನಡುವೆ ಸುತ್ತುವರಿದ ಅನಿಯಮಿತ (ಅನಂತ) ಕರ್ವಿಲಿನಿಯರ್ ಟ್ರೆಪೆಜಾಯಿಡ್ನ ಪ್ರದೇಶವನ್ನು ವ್ಯಕ್ತಪಡಿಸುತ್ತದೆ. ವೈ = f(X) (ಕೆಳಗಿನ ಚಿತ್ರದಲ್ಲಿ - ಕೆಂಪು), X = ಎಮತ್ತು ಅಬ್ಸಿಸ್ಸಾ ಅಕ್ಷ.

ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಇತರ ಅನಂತ ಮಧ್ಯಂತರಗಳಿಗೆ ಇದೇ ರೀತಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

ಅನಂತ ಬಾಗಿದ ಟ್ರೆಪೆಜಾಯಿಡ್ನ ಪ್ರದೇಶವು ಸೀಮಿತ ಸಂಖ್ಯೆಯಾಗಿರಬಹುದು, ಈ ಸಂದರ್ಭದಲ್ಲಿ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಒಮ್ಮುಖ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಪ್ರದೇಶವು ಅನಂತವಾಗಿರಬಹುದು, ಮತ್ತು ಈ ಸಂದರ್ಭದಲ್ಲಿ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಡೈವರ್ಜೆಂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಕ್ಕೆ ಬದಲಾಗಿ ಅವಿಭಾಜ್ಯ ಮಿತಿಯನ್ನು ಬಳಸುವುದು.ಅನುಚಿತ ಅವಿಭಾಜ್ಯವನ್ನು ಮೌಲ್ಯಮಾಪನ ಮಾಡಲು, ನೀವು ನಿರ್ದಿಷ್ಟ ಅವಿಭಾಜ್ಯ ಮಿತಿಯನ್ನು ಬಳಸಬೇಕಾಗುತ್ತದೆ. ಈ ಮಿತಿಯು ಅಸ್ತಿತ್ವದಲ್ಲಿದ್ದರೆ ಮತ್ತು ಸೀಮಿತವಾಗಿದ್ದರೆ (ಅನಂತಕ್ಕೆ ಸಮಾನವಾಗಿಲ್ಲ), ನಂತರ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಒಮ್ಮುಖ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಮತ್ತು ಇಲ್ಲದಿದ್ದರೆ - ವಿಭಿನ್ನವಾಗಿರುತ್ತದೆ. ಮಿತಿ ಚಿಹ್ನೆಯ ಅಡಿಯಲ್ಲಿ ಯಾವ ವೇರಿಯಬಲ್ ಒಲವು ತೋರುತ್ತದೆ ಎಂಬುದು ನಾವು ಮೊದಲ ವಿಧದ ಅಥವಾ ಎರಡನೆಯ ರೀತಿಯ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯದೊಂದಿಗೆ ವ್ಯವಹರಿಸುತ್ತಿದ್ದೇವೆಯೇ ಎಂಬುದರ ಮೇಲೆ ಅವಲಂಬಿತವಾಗಿರುತ್ತದೆ. ಇದರ ಬಗ್ಗೆ ಈಗ ತಿಳಿದುಕೊಳ್ಳೋಣ.

ಮೊದಲ ವಿಧದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳು - ಅನಂತ ಮಿತಿಗಳು ಮತ್ತು ಅವುಗಳ ಒಮ್ಮುಖದೊಂದಿಗೆ

ಅನಂತ ಮೇಲಿನ ಮಿತಿಯೊಂದಿಗೆ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳು

ಆದ್ದರಿಂದ, ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಬರೆಯುವುದು ಸಾಮಾನ್ಯ ನಿರ್ದಿಷ್ಟ ಅವಿಭಾಜ್ಯಕ್ಕಿಂತ ಭಿನ್ನವಾಗಿರುತ್ತದೆ, ಇದರಲ್ಲಿ ಏಕೀಕರಣದ ಮೇಲಿನ ಮಿತಿಯು ಅನಂತವಾಗಿರುತ್ತದೆ.

ವ್ಯಾಖ್ಯಾನ. ನಿರಂತರ ಕಾರ್ಯದ ಏಕೀಕರಣದ ಅನಂತ ಮೇಲಿನ ಮಿತಿಯೊಂದಿಗೆ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯ f(X) ನಿಂದ ಮಧ್ಯಂತರದಲ್ಲಿ ಎ ಮೊದಲು ∞ ಏಕೀಕರಣದ ಮೇಲಿನ ಮಿತಿಯೊಂದಿಗೆ ಈ ಕಾರ್ಯದ ಅವಿಭಾಜ್ಯ ಮಿತಿಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಬಿ ಮತ್ತು ಏಕೀಕರಣದ ಕಡಿಮೆ ಮಿತಿ ಎ ಏಕೀಕರಣದ ಮೇಲಿನ ಮಿತಿಯು ಮಿತಿಯಿಲ್ಲದೆ ಬೆಳೆಯುತ್ತದೆ, ಅಂದರೆ

.

ಈ ಮಿತಿಯು ಅಸ್ತಿತ್ವದಲ್ಲಿದ್ದರೆ ಮತ್ತು ಅನಂತಕ್ಕಿಂತ ಕೆಲವು ಸಂಖ್ಯೆಗಳಿಗೆ ಸಮನಾಗಿದ್ದರೆ, ಆಗ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಒಮ್ಮುಖ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಮತ್ತು ಮಿತಿಯು ಸಮಾನವಾಗಿರುವ ಸಂಖ್ಯೆಯನ್ನು ಅದರ ಮೌಲ್ಯವಾಗಿ ತೆಗೆದುಕೊಳ್ಳಲಾಗುತ್ತದೆ. ಇಲ್ಲದಿದ್ದರೆ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಡೈವರ್ಜೆಂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆಮತ್ತು ಅದಕ್ಕೆ ಯಾವುದೇ ಅರ್ಥವನ್ನು ಹೇಳಲಾಗುವುದಿಲ್ಲ.

ಉದಾಹರಣೆ 1. ಅನುಚಿತ ಅವಿಭಾಜ್ಯವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಿ(ಅದು ಒಮ್ಮುಖವಾಗಿದ್ದರೆ).

ಪರಿಹಾರ. ಅನುಚಿತ ಅವಿಭಾಜ್ಯ ವ್ಯಾಖ್ಯಾನದ ಆಧಾರದ ಮೇಲೆ, ನಾವು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ

ಮಿತಿಯು ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ ಮತ್ತು 1 ಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ, ನಂತರ ಇದು ಅನುಚಿತ ಅವಿಭಾಜ್ಯ ಒಮ್ಮುಖಗಳುಮತ್ತು 1 ಕ್ಕೆ ಸಮಾನವಾಗಿರುತ್ತದೆ.

ಕೆಳಗಿನ ಉದಾಹರಣೆಯಲ್ಲಿ, ಇಂಟಿಗ್ರ್ಯಾಂಡ್ ಉದಾಹರಣೆ 1 ರಲ್ಲಿನಂತೆಯೇ ಇರುತ್ತದೆ, ಕೇವಲ ಡಿಗ್ರಿ x ಎರಡು ಅಲ್ಲ, ಆದರೆ ಅಕ್ಷರದ ಆಲ್ಫಾ, ಮತ್ತು ಕಾರ್ಯವು ಒಮ್ಮುಖವಾಗಲು ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಅಧ್ಯಯನ ಮಾಡುವುದು. ಅಂದರೆ, ಪ್ರಶ್ನೆಗೆ ಉತ್ತರಿಸಬೇಕಾಗಿದೆ: ಈ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವು ಆಲ್ಫಾದ ಯಾವ ಮೌಲ್ಯಗಳಲ್ಲಿ ಒಮ್ಮುಖವಾಗುತ್ತದೆ ಮತ್ತು ಅದು ಯಾವ ಮೌಲ್ಯಗಳಲ್ಲಿ ಭಿನ್ನವಾಗಿರುತ್ತದೆ?

ಉದಾಹರಣೆ 2. ಒಮ್ಮುಖವಾಗಲು ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಪರೀಕ್ಷಿಸಿ(ಏಕೀಕರಣದ ಕಡಿಮೆ ಮಿತಿಯು ಶೂನ್ಯಕ್ಕಿಂತ ಹೆಚ್ಚಾಗಿರುತ್ತದೆ).

ಪರಿಹಾರ. ಅದನ್ನು ಮೊದಲು ಊಹಿಸೋಣ, ನಂತರ

ಪರಿಣಾಮವಾಗಿ ಅಭಿವ್ಯಕ್ತಿಯಲ್ಲಿ, ನಾವು ಮಿತಿಗೆ ಹೋಗುತ್ತೇವೆ:

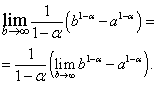
ಬಲಭಾಗದಲ್ಲಿರುವ ಮಿತಿಯು ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ ಮತ್ತು ಶೂನ್ಯಕ್ಕೆ ಸಮನಾಗಿರುತ್ತದೆ, ಅಂದರೆ, ಮತ್ತು ಯಾವಾಗ ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲ, ಅಂದರೆ.

ಮೊದಲ ಸಂದರ್ಭದಲ್ಲಿ, ಅಂದರೆ, ಯಾವಾಗ . ವೇಳೆ, ನಂತರ ಮತ್ತು ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲ.

ನಮ್ಮ ಅಧ್ಯಯನದ ತೀರ್ಮಾನವು ಈ ಕೆಳಗಿನಂತಿರುತ್ತದೆ: ಇದು ಅನುಚಿತ ಅವಿಭಾಜ್ಯ ಒಮ್ಮುಖಗಳುನಲ್ಲಿ ಮತ್ತು ಭಿನ್ನವಾಗಿಸುತ್ತದೆನಲ್ಲಿ.

ನ್ಯೂಟನ್-ಲೀಬ್ನಿಜ್ ಸೂತ್ರವನ್ನು ಅಧ್ಯಯನ ಮಾಡಲಾಗುತ್ತಿರುವ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯ ಪ್ರಕಾರಕ್ಕೆ ಅನ್ವಯಿಸುವುದು , ನೀವು ಈ ಕೆಳಗಿನ ಸೂತ್ರವನ್ನು ಪಡೆಯಬಹುದು, ಅದು ತುಂಬಾ ಹೋಲುತ್ತದೆ:

.

ಇದು ಸಾಮಾನ್ಯೀಕರಿಸಿದ ನ್ಯೂಟನ್-ಲೀಬ್ನಿಜ್ ಸೂತ್ರವಾಗಿದೆ.

ಉದಾಹರಣೆ 3. ಅನುಚಿತ ಅವಿಭಾಜ್ಯವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಿ(ಅದು ಒಮ್ಮುಖವಾಗಿದ್ದರೆ).

ಈ ಸಮಗ್ರತೆಯ ಮಿತಿಯು ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ:

ಎರಡನೇ ಅವಿಭಾಜ್ಯ, ಮೂಲ ಅವಿಭಾಜ್ಯವನ್ನು ವ್ಯಕ್ತಪಡಿಸುವ ಮೊತ್ತವನ್ನು ರೂಪಿಸುತ್ತದೆ:

ಈ ಅವಿಭಾಜ್ಯ ಮಿತಿಯು ಸಹ ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ:

.

ನಾವು ಎರಡು ಅವಿಭಾಜ್ಯಗಳ ಮೊತ್ತವನ್ನು ಕಂಡುಕೊಳ್ಳುತ್ತೇವೆ, ಇದು ಎರಡು ಅನಂತ ಮಿತಿಗಳೊಂದಿಗೆ ಮೂಲ ಅನುಚಿತ ಅವಿಭಾಜ್ಯ ಮೌಲ್ಯವಾಗಿದೆ:

ಎರಡನೇ ವಿಧದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳು - ಮಿತಿಯಿಲ್ಲದ ಕಾರ್ಯಗಳು ಮತ್ತು ಅವುಗಳ ಒಮ್ಮುಖದಿಂದ

ಕಾರ್ಯ ಮಾಡಲಿ f(X) ನಿಂದ ವಿಭಾಗದಲ್ಲಿ ನೀಡಲಾಗಿದೆ ಎ ಮೊದಲು ಬಿ ಮತ್ತು ಅದರ ಮೇಲೆ ಅನಿಯಮಿತವಾಗಿದೆ. ಕ್ರಿಯೆಯು ಹಂತದಲ್ಲಿ ಅನಂತಕ್ಕೆ ಹೋಗುತ್ತದೆ ಎಂದು ಭಾವಿಸೋಣ ಬಿ , ವಿಭಾಗದ ಎಲ್ಲಾ ಇತರ ಬಿಂದುಗಳಲ್ಲಿ ಇದು ನಿರಂತರವಾಗಿರುತ್ತದೆ.

ವ್ಯಾಖ್ಯಾನ. ಒಂದು ಕಾರ್ಯದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯ f(X) ನಿಂದ ವಿಭಾಗದಲ್ಲಿ ಎ ಮೊದಲು ಬಿ ಏಕೀಕರಣದ ಮೇಲಿನ ಮಿತಿಯೊಂದಿಗೆ ಈ ಕಾರ್ಯದ ಅವಿಭಾಜ್ಯ ಮಿತಿಯನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ ಸಿ , ಪ್ರಯತ್ನಿಸುವಾಗ ಸಿ ಗೆ ಬಿ ಕಾರ್ಯವು ಮಿತಿಯಿಲ್ಲದೆ ಮತ್ತು ಹಂತದಲ್ಲಿ ಹೆಚ್ಚಾಗುತ್ತದೆ X = ಬಿ ಕಾರ್ಯವನ್ನು ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿಲ್ಲ, ಅಂದರೆ

.

ಈ ಮಿತಿಯು ಅಸ್ತಿತ್ವದಲ್ಲಿದ್ದರೆ, ಎರಡನೆಯ ವಿಧದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಒಮ್ಮುಖ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ, ಇಲ್ಲದಿದ್ದರೆ ಅದನ್ನು ಡೈವರ್ಜೆಂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

ನ್ಯೂಟನ್-ಲೀಬ್ನಿಜ್ ಸೂತ್ರವನ್ನು ಬಳಸಿ, ನಾವು ಪಡೆಯುತ್ತೇವೆ.

1. ಅನಂತ ಮಿತಿಗಳೊಂದಿಗೆ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳು

ಅವಿಭಾಜ್ಯ ಮೊತ್ತಗಳ ಮಿತಿಯಾಗಿ ಅವಿಭಾಜ್ಯ ವ್ಯಾಖ್ಯಾನವನ್ನು ನಾವು ನೆನಪಿಸಿಕೊಳ್ಳೋಣ:

ಏಕೀಕರಣ ಮಧ್ಯಂತರವು ಸೀಮಿತವಾಗಿದೆ ಮತ್ತು f(x) ಕಾರ್ಯವು ಅದರೊಳಗೆ ನಿರಂತರವಾಗಿರುತ್ತದೆ ಎಂದು ವ್ಯಾಖ್ಯಾನವು ಊಹಿಸುತ್ತದೆ. ಈ ಊಹೆಗಳ ಉಲ್ಲಂಘನೆಯು ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಕಾರಣವಾಗುತ್ತದೆ.

ವ್ಯಾಖ್ಯಾನ.ಅವಿಭಾಜ್ಯವು ಸೀಮಿತ ಮಿತಿಗೆ ಒಲವು ತೋರಿದರೆ ಅದು ಅನಿರ್ದಿಷ್ಟವಾಗಿ ಹೆಚ್ಚಾಗುತ್ತದೆ "ಬಿ", ನಂತರ ಈ ಮಿತಿಯನ್ನು f (x) ಫಂಕ್ಷನ್‌ನ ಅನಂತ ಮೇಲಿನ ಬೌಂಡ್‌ನೊಂದಿಗೆ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು ಇದನ್ನು ಚಿಹ್ನೆಯಿಂದ ಸೂಚಿಸಲಾಗುತ್ತದೆ

ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವು ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ ಅಥವಾ ಒಮ್ಮುಖವಾಗುತ್ತದೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ.

ನಿರ್ದಿಷ್ಟಪಡಿಸಿದ ಮಿತಿಯು ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲ ಅಥವಾ ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲ ಆದರೆ ಅನಂತವಾಗಿದ್ದರೆ, ಆಗ ಅವಿಭಾಜ್ಯವು ಅಸ್ತಿತ್ವದಲ್ಲಿಲ್ಲ ಅಥವಾ ಬೇರೆಯಾಗುವುದು ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ.

ಅನಂತ ಕೆಳಗಿನ ಬೌಂಡ್‌ನೊಂದಿಗೆ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಇದೇ ರೀತಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

ಎರಡು ಅನಂತ ಗಡಿಗಳನ್ನು ಹೊಂದಿರುವ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಇವರಿಂದ ನೀಡಲಾಗಿದೆ:

ಇಲ್ಲಿ c ಎಂಬುದು ಆಕ್ಸ್ ಅಕ್ಷದ ಯಾವುದೇ ಸ್ಥಿರ ಬಿಂದುವಾಗಿದೆ.

ಆದ್ದರಿಂದ, ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳು ಅನಂತ ಕೆಳಗಿನ ಬೌಂಡ್, ಅನಂತ ಮೇಲಿನ ಬೌಂಡ್ ಮತ್ತು ಎರಡು ಅನಂತ ಗಡಿಗಳನ್ನು ಹೊಂದಬಹುದು.

ಒಮ್ಮುಖದ ಚಿಹ್ನೆಗಳು. ಸಂಪೂರ್ಣ ಮತ್ತು ಷರತ್ತುಬದ್ಧ ಒಮ್ಮುಖ

ಪ್ರತಿಯೊಂದು ಅವಿಭಾಜ್ಯಗಳು ಅಸ್ತಿತ್ವದಲ್ಲಿದ್ದರೆ ಮಾತ್ರ ಅವಿಭಾಜ್ಯವು ಅಸ್ತಿತ್ವದಲ್ಲಿದೆ: ಮತ್ತು .

ಉದಾಹರಣೆ.ಸಮಗ್ರತೆಯ ಒಮ್ಮುಖವನ್ನು ಪರೀಕ್ಷಿಸಿ

c = 0 ಎಂದು ಭಾವಿಸಿದರೆ, ನಾವು ಪಡೆಯುತ್ತೇವೆ:

ಆ. ಅವಿಭಾಜ್ಯ ಒಮ್ಮುಖವಾಗುತ್ತದೆ.

ಕೆಲವೊಮ್ಮೆ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡುವ ಅಗತ್ಯವಿಲ್ಲ, ಆದರೆ ಅದನ್ನು ಮತ್ತೊಂದು ಅವಿಭಾಜ್ಯದೊಂದಿಗೆ ಹೋಲಿಸುವ ಮೂಲಕ ಅದು ಒಮ್ಮುಖವಾಗುತ್ತದೆಯೇ ಅಥವಾ ಭಿನ್ನವಾಗಿರುತ್ತದೆಯೇ ಎಂದು ತಿಳಿದುಕೊಳ್ಳುವುದು ಸಾಕು.

ಅನುಚಿತ ಅವಿಭಾಜ್ಯಗಳಿಗೆ ಹೋಲಿಕೆ ಪ್ರಮೇಯ.

ಮಧ್ಯಂತರದಲ್ಲಿ f (x) ಕಾರ್ಯವು ಮೊದಲ ವಿಧದ ಹಲವಾರು (ಸೀಮಿತ ಸಂಖ್ಯೆ) ಸ್ಥಗಿತದ ಬಿಂದುಗಳನ್ನು ಹೊಂದಿರಲಿ, ಈ "ಅಡೆತಡೆಯನ್ನು" ವಿಭಾಗವನ್ನು ಸ್ಥಗಿತದ ಬಿಂದುಗಳೊಂದಿಗೆ ಹಲವಾರು ವಿಭಾಗಗಳಾಗಿ ವಿಭಜಿಸುವ ಮೂಲಕ ಸುಲಭವಾಗಿ ನಿರ್ಮೂಲನೆ ಮಾಡಬಹುದು, ಪ್ರತಿಯೊಂದು ವಿಭಾಗದಲ್ಲೂ ನಿರ್ದಿಷ್ಟ ಅವಿಭಾಜ್ಯಗಳನ್ನು ಲೆಕ್ಕಹಾಕುವುದು ಮತ್ತು ಫಲಿತಾಂಶಗಳನ್ನು ಸೇರಿಸುವುದು.

ವಿಭಾಗದ ತುದಿಗಳಲ್ಲಿ ಒಂದನ್ನು ಸಮೀಪಿಸುವಾಗ ಅನಿಯಮಿತವಾದ ಕಾರ್ಯದ ನಿರ್ದಿಷ್ಟ ಅವಿಭಾಜ್ಯವನ್ನು ನಾವು ಪರಿಗಣಿಸೋಣ, ಉದಾಹರಣೆಗೆ, .

(ಅಂತಹ ಸಂದರ್ಭಗಳಲ್ಲಿ ಅವರು ಸಾಮಾನ್ಯವಾಗಿ ಹೇಳುತ್ತಾರೆ: ''ಕಾರ್ಯವು ಏಕೀಕರಣದ ಮಧ್ಯಂತರದ ಬಲ ತುದಿಯಲ್ಲಿ ಅನಂತ ಸ್ಥಗಿತವನ್ನು ಹೊಂದಿದೆ''.)

ಸಮಗ್ರತೆಯ ಸಾಮಾನ್ಯ ವ್ಯಾಖ್ಯಾನವು ಇಲ್ಲಿ ಅದರ ಅರ್ಥವನ್ನು ಕಳೆದುಕೊಳ್ಳುತ್ತದೆ ಎಂಬುದು ಸ್ಪಷ್ಟವಾಗಿದೆ.

ವ್ಯಾಖ್ಯಾನ. f(x) ಕಾರ್ಯದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯ, £ x ಗೆ ನಿರಂತರವಾಗಿರುತ್ತದೆ< b и неограниченной при x ® b - 0, называется предел:

ವಿಭಾಗದ ಎಡ ತುದಿಯಲ್ಲಿ ಅನಂತ ಸ್ಥಗಿತವನ್ನು ಹೊಂದಿರುವ ಕಾರ್ಯದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಇದೇ ರೀತಿ ವ್ಯಾಖ್ಯಾನಿಸಲಾಗಿದೆ:

ಪರಿಣಾಮವಾಗಿ, ವಿಭಾಗದಲ್ಲಿ [-1, 0] ಅವಿಭಾಜ್ಯವು ಭಿನ್ನವಾಗಿರುತ್ತದೆ.

ಇದರರ್ಥ ಅವಿಭಾಜ್ಯವು ವಿಭಾಗದಲ್ಲಿಯೂ ಭಿನ್ನವಾಗಿರುತ್ತದೆ.

ಹೀಗಾಗಿ, ಈ ಅವಿಭಾಜ್ಯವು ಸಂಪೂರ್ಣ ಮಧ್ಯಂತರದಲ್ಲಿ [-1, 1] ಭಿನ್ನವಾಗಿರುತ್ತದೆ. x = 0 ಬಿಂದುವಿನಲ್ಲಿ ಇಂಟಿಗ್ರ್ಯಾಂಡ್‌ನ ಸ್ಥಗಿತಕ್ಕೆ ಗಮನ ಕೊಡದೆ ನಾವು ಈ ಅವಿಭಾಜ್ಯವನ್ನು ಲೆಕ್ಕಾಚಾರ ಮಾಡಲು ಪ್ರಾರಂಭಿಸಿದರೆ, ನಾವು ತಪ್ಪಾದ ಫಲಿತಾಂಶವನ್ನು ಪಡೆಯುತ್ತೇವೆ ಎಂಬುದನ್ನು ಗಮನಿಸಿ. ನಿಜವಾಗಿಯೂ,

, ಇದು ಅಸಾಧ್ಯ.

ಆದ್ದರಿಂದ, ನಿರಂತರ ಕ್ರಿಯೆಯ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವನ್ನು ಅಧ್ಯಯನ ಮಾಡಲು, ಅದನ್ನು ಹಲವಾರು ಅವಿಭಾಜ್ಯಗಳಾಗಿ "ವಿಭಜಿಸುವುದು" ಮತ್ತು ಅವುಗಳನ್ನು ಅಧ್ಯಯನ ಮಾಡುವುದು ಅವಶ್ಯಕ.

ಏಕೀಕರಣದ (ಸೀಮಿತ) ಮಧ್ಯಂತರದಲ್ಲಿ ಅವಿಭಾಜ್ಯವು ಎರಡನೇ ವಿಧದ ಸ್ಥಗಿತವನ್ನು ಹೊಂದಿದ್ದರೆ, ನಾವು ಎರಡನೇ ವಿಧದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯತೆಯ ಬಗ್ಗೆ ಮಾತನಾಡುತ್ತೇವೆ.

10.2.1 ವ್ಯಾಖ್ಯಾನ ಮತ್ತು ಮೂಲ ಗುಣಲಕ್ಷಣಗಳು

ನಾವು ಏಕೀಕರಣದ ಮಧ್ಯಂತರವನ್ನು $\left [ a, \, b \right ]$ ನಿಂದ ಸೂಚಿಸೋಣ; ಈ ಎರಡೂ ಸಂಖ್ಯೆಗಳನ್ನು ಕೆಳಗೆ ಸೀಮಿತ ಎಂದು ಭಾವಿಸಲಾಗಿದೆ. ಕೇವಲ 1 ಸ್ಥಗಿತವಾಗಿದ್ದರೆ, ಅದನ್ನು $a$ ನಲ್ಲಿ ಅಥವಾ ಪಾಯಿಂಟ್ $b$ ನಲ್ಲಿ ಅಥವಾ ಮಧ್ಯಂತರ $(a,\,b)$ ನಲ್ಲಿ ಇರಿಸಬಹುದು. ಬಿಂದು $a$ ನಲ್ಲಿ ಎರಡನೇ ರೀತಿಯ ಸ್ಥಗಿತಗೊಂಡಾಗ ನಾವು ಮೊದಲು ಪ್ರಕರಣವನ್ನು ಪರಿಗಣಿಸೋಣ ಮತ್ತು ಇತರ ಹಂತಗಳಲ್ಲಿ ಸಮಗ್ರ ಕಾರ್ಯವು ನಿರಂತರವಾಗಿರುತ್ತದೆ. ಆದ್ದರಿಂದ ನಾವು ಸಮಗ್ರತೆಯನ್ನು ಚರ್ಚಿಸುತ್ತಿದ್ದೇವೆ

\begin(ಸಮೀಕರಣ) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(ಸಮೀಕರಣ)

ಮತ್ತು $f(x) \rightarrow \infty $ ಯಾವಾಗ $x \rightarrow a+0$. ಮೊದಲಿನಂತೆ, ಈ ಅಭಿವ್ಯಕ್ತಿಗೆ ಅರ್ಥವನ್ನು ನೀಡುವುದು ಮೊದಲನೆಯದು. ಇದನ್ನು ಮಾಡಲು, ಅವಿಭಾಜ್ಯವನ್ನು ಪರಿಗಣಿಸಿ

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

ವ್ಯಾಖ್ಯಾನ. ಸೀಮಿತ ಮಿತಿ ಇರಲಿ

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

ನಂತರ ಎರಡನೇ ವಿಧದ (22) ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯವು ಒಮ್ಮುಖವಾಗುತ್ತದೆ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ ಮತ್ತು ಅದಕ್ಕೆ $A$ ಮೌಲ್ಯವನ್ನು ನಿಗದಿಪಡಿಸಲಾಗಿದೆ; $f(x)$ ಕಾರ್ಯವು $\ಎಡ[ a, \ ಮಧ್ಯಂತರದಲ್ಲಿ ಇಂಟಿಗ್ರಬಲ್ ಎಂದು ಹೇಳಲಾಗುತ್ತದೆ. , b\right]$.

ಏಕೀಕರಣದ ಮಧ್ಯಂತರದ ಮೇಲಿನ ಮಿತಿಯಲ್ಲಿ ಇಂಟಿಗ್ರ್ಯಾಂಡ್ ಫಂಕ್ಷನ್‌ನಲ್ಲಿ ಎರಡನೇ ರೀತಿಯ ಸ್ಥಗಿತಗೊಂಡಾಗ ನಾವು ಆಯ್ಕೆಯನ್ನು ಪರಿಗಣಿಸೋಣ. $x=-t$ ವೇರಿಯಬಲ್‌ನ ಬದಲಾವಣೆಯನ್ನು ಮಾಡುವ ಮೂಲಕ ಮತ್ತು ನಂತರ ಏಕೀಕರಣದ ಮಿತಿಗಳನ್ನು ಮರುಹೊಂದಿಸುವ ಮೂಲಕ ಈ ಪ್ರಕರಣವನ್ನು ಹಿಂದಿನದಕ್ಕೆ ಕಡಿಮೆ ಮಾಡಬಹುದು.

ಇಂಟಿಗ್ರ್ಯಾಂಡ್ ಫಂಕ್ಷನ್ $c \in (a,\,b)$ ನಲ್ಲಿ ಏಕೀಕರಣ ಮಧ್ಯಂತರದಲ್ಲಿ ಎರಡನೇ ರೀತಿಯ ಸ್ಥಗಿತವನ್ನು ಹೊಂದಿರುವಾಗ ನಾವು ಆಯ್ಕೆಯನ್ನು ಪರಿಗಣಿಸೋಣ. ಈ ಸಂದರ್ಭದಲ್ಲಿ, ಮೂಲ ಅವಿಭಾಜ್ಯ

\begin(ಸಮೀಕರಣ) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(ಸಮೀಕರಣ)

ಮೊತ್ತವಾಗಿ ಪ್ರಸ್ತುತಪಡಿಸಲಾಗಿದೆ

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

ವ್ಯಾಖ್ಯಾನ. ಎರಡೂ ಅವಿಭಾಜ್ಯಗಳು $I_1, \, I_2$ ಒಮ್ಮುಖವಾಗಿದ್ದರೆ, ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯ (23) ಅನ್ನು ಒಮ್ಮುಖ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ ಮತ್ತು $I_1, \, I_2$, ಫಂಕ್ಷನ್ $f(x)$ ಮೊತ್ತಕ್ಕೆ ಸಮಾನವಾದ ಮೌಲ್ಯವನ್ನು ನಿಗದಿಪಡಿಸಲಾಗಿದೆ $\ಎಡ [a, \, b\right]$ ಮಧ್ಯಂತರದಲ್ಲಿ ಇಂಟಿಗ್ರೇಬಲ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ. ಕನಿಷ್ಠ ಒಂದು ಅವಿಭಾಜ್ಯ $I_1,\, I_2$ ಭಿನ್ನವಾಗಿದ್ದರೆ, ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯ (23) ಅನ್ನು ಡೈವರ್ಜೆಂಟ್ ಎಂದು ಕರೆಯಲಾಗುತ್ತದೆ.

2 ನೇ ವಿಧದ ಒಮ್ಮುಖ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳು ಸಾಮಾನ್ಯ ನಿರ್ದಿಷ್ಟ ಅವಿಭಾಜ್ಯಗಳ ಎಲ್ಲಾ ಪ್ರಮಾಣಿತ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಹೊಂದಿವೆ.

1. $\ಎಡ[ a, \,b \right ]$ ಮಧ್ಯಂತರದಲ್ಲಿ $f(x)$, $g(x)$ ಇಂಟಿಗ್ರಬಲ್ ಆಗಿದ್ದರೆ, ಅವುಗಳ ಮೊತ್ತ $f(x)+g(x)$ ಆಗಿದೆ ಈ ಮಧ್ಯಂತರದಲ್ಲಿ ಸಹ ಸಂಯೋಜಿಸಬಹುದಾಗಿದೆ, ಮತ್ತು \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. $\ಎಡ[ a, \, b \right ]$ ಮಧ್ಯಂತರದಲ್ಲಿ $f(x)$ ಇಂಟಿಗ್ರೇಬಲ್ ಆಗಿದ್ದರೆ, ಯಾವುದೇ ಸ್ಥಿರ $C$ ಗೆ $C\cdot f(x)$ ಕೂಡ ಈ ಮಧ್ಯಂತರದಲ್ಲಿ ಇಂಟಿಗ್ರೇಬಲ್, ಮತ್ತು \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. $f(x)$ ಮಧ್ಯಂತರದಲ್ಲಿ ಸಂಯೋಜಿತವಾಗಿದ್ದರೆ $\ಎಡ[ a, \, b \right ]$, ಮತ್ತು ಈ ಮಧ್ಯಂತರದಲ್ಲಿ $f(x)>0$, ನಂತರ \[ \int _a^ (b ) f(x)dx\,>\,0. \] 4. $\ಎಡ[ a, \, b \right ]$ ಮಧ್ಯಂತರದಲ್ಲಿ $f(x)$ ಇಂಟಿಗ್ರಬಲ್ ಆಗಿದ್ದರೆ, ನಂತರ ಯಾವುದೇ $c\in (a, \,b)$ ಗೆ ಇಂಟಿಗ್ರಲ್ಸ್ \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] ಕೂಡ ಒಮ್ಮುಖವಾಗುತ್ತದೆ, ಮತ್ತು \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (ಮಧ್ಯಂತರದಲ್ಲಿ ಅವಿಭಾಜ್ಯತೆಯ ಸಂಕಲನ).

ಅವಿಭಾಜ್ಯವನ್ನು ಪರಿಗಣಿಸಿ

\begin(ಸಮೀಕರಣ) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(ಸಮೀಕರಣ)

$k>0$ ಆಗಿದ್ದರೆ, ಇಂಟಿಗ್ರ್ಯಾಂಡ್ $\infty$ ಗೆ $x \rightarrow +0$ ಎಂದು ಒಲವು ತೋರುತ್ತದೆ, ಆದ್ದರಿಂದ ಅವಿಭಾಜ್ಯವು ಎರಡನೇ ವಿಧದ ಅನುಚಿತವಾಗಿದೆ. ಕಾರ್ಯವನ್ನು ಪರಿಚಯಿಸೋಣ

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

ಈ ಸಂದರ್ಭದಲ್ಲಿ ಆಂಟಿಡೆರಿವೇಟಿವ್ ಅನ್ನು ಕರೆಯಲಾಗುತ್ತದೆ, ಆದ್ದರಿಂದ

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

$k ಗೆ \neq 1$,

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

$k = 1$ ಗೆ. $\epsilon \rightarrow +0$ ನಲ್ಲಿನ ನಡವಳಿಕೆಯನ್ನು ಪರಿಗಣಿಸಿ, ಸಮಗ್ರ (20) $k ನಲ್ಲಿ ಒಮ್ಮುಖವಾಗುತ್ತದೆ ಎಂಬ ತೀರ್ಮಾನಕ್ಕೆ ನಾವು ಬರುತ್ತೇವೆ

10.2.2 2 ನೇ ವಿಧದ ಅಸಮರ್ಪಕ ಅವಿಭಾಜ್ಯಗಳ ಒಮ್ಮುಖಕ್ಕೆ ಪರೀಕ್ಷೆಗಳು

ಪ್ರಮೇಯ (ಹೋಲಿಕೆಯ ಮೊದಲ ಚಿಹ್ನೆ). $x\in (a,\,b)$ ಮತ್ತು $0 1 ಗೆ $f(x)$, $g(x)$ ನಿರಂತರವಾಗಿರಲಿ. \[ \int _a^(b)g(x) dx \] ಒಮ್ಮುಖವಾಗುತ್ತದೆ, ನಂತರ ಅವಿಭಾಜ್ಯ \[ \int _a^(b)f(x)dx ಒಮ್ಮುಖವಾಗುತ್ತದೆ. \] 2. ಅವಿಭಾಜ್ಯ \[ \int _a^(b)f(x)dx \] ಬೇರೆಡೆಗೆ ತಿರುಗಿದರೆ, \[ \int _a^(b)g(x)dx ಭಿನ್ನವಾಗಿರುತ್ತದೆ. \]

ಪ್ರಮೇಯ (ಎರಡನೇ ಹೋಲಿಕೆ ಮಾನದಂಡ). $x\in (a,\,b)$ ಗೆ $f(x)$, $g(x)$ ನಿರಂತರ ಮತ್ತು ಧನಾತ್ಮಕವಾಗಿರಲಿ ಮತ್ತು ಸೀಮಿತ ಮಿತಿ ಇರಲಿ

\[ \theta = \lim_(x \rightarrow a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

ನಂತರ ಅವಿಭಾಜ್ಯಗಳು

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

ಏಕಕಾಲದಲ್ಲಿ ಒಮ್ಮುಖವಾಗು ಅಥವಾ ಭಿನ್ನವಾಗು.