Колку изнесува збирот на аглите? Теорема за збирот на аглите на триаголникот. Видови според големината на аголот

Збир на агли на триаголник- важно, но доволно едноставна тема, која се изучува во 7-мо одделение геометрија. Темата се состои од теорема, краток доказ и неколку логички последици. Познавањето на оваа тема помага во решавањето геометриски проблемипри последователно проучување на предметот.

Теорема - кои се аглите на произволен триаголник собрани заедно?

Теоремата вели дека ако земете кој било триаголник, без оглед на неговиот тип, збирот на сите агли секогаш ќе биде 180 степени. Ова се докажува на следниов начин:

• на пример, земете го триаголникот ABC, повлечете права линија низ точката B која се наоѓа на врвот и означете ја како „а“, правата линија „а“ е строго паралелна со страната AC;
• помеѓу права линија „а“ и страните AB и BC, се означуваат агли, означувајќи ги со броевите 1 и 2;
• аголот 1 се смета за еднаков на аголот А, а аголот 2 се смета за еднаков на аголот C, бидејќи се смета дека овие агли лежат попречно;
• така, збирот помеѓу аглите 1, 2 и 3 (кој е означен на местото на аголот Б) се препознава како еднаков на расклопениот агол со темето B - и е 180 степени.

Ако збирот на аглите означени со бројки е 180 степени, тогаш збирот на аглите A, B и C се препознава како еднаков на 180 степени. Ова правило важи за секој триаголник.

Што следи од геометриската теорема

Вообичаено е да се истакнат неколку последици од горната теорема.

• Ако проблемот разгледа триаголник со прав агол, тогаш еден од неговите агли стандардно ќе биде еднаков на 90 степени, а збирот на акутните агли исто така ќе биде 90 степени.
• Ако зборуваме за правоаголен рамнокрак триаголник, тогаш неговите остри агли, кои се собираат до 90 степени, поединечно ќе бидат еднакви на 45 степени.
• Рамностран триаголник се состои од три еднакви агли, соодветно, секој од нив ќе биде еднаков на 60 степени, а вкупно тие ќе бидат 180 степени.
• Надворешниот агол на кој било триаголник ќе биде еднаков на збирот помеѓу два внатрешни агли кои не се блиску до него.

Може да се изведе следново правило: секој триаголник има најмалку два остри агли. Во некои случаи, триаголникот се состои од три остри агли, а ако има само два, тогаш третиот агол ќе биде тап или правилен.

Теорема. Збирот на внатрешните агли на триаголникот е еднаков на два прави агли.

Да земеме некој триаголник ABC (сл. 208). Да ги означиме неговите внатрешни агли со броевите 1, 2 и 3. Да го докажеме тоа

∠1 + ∠2 + ∠3 = 180°.

Дозволете ни да нацртаме низ некое теме на триаголникот, на пример B, права линија MN паралелна на AC.

На темето B добивме три агли: ∠4, ∠2 и ∠5. Нивниот збир е прав агол, затоа е еднаков на 180 °:

∠4 + ∠2 + ∠5 = 180°.

Но, ∠4 = ∠1 се внатрешни попречни агли со паралелни прави MN и AC и секент AB.

∠5 = ∠3 - тоа се внатрешни попречни агли со паралелни прави MN и AC и секент BC.

Ова значи дека ∠4 и ∠5 може да се заменат со нивните еднакви ∠1 и ∠3.

Затоа, ∠1 + ∠2 + ∠3 = 180°. Теоремата е докажана.

2. Својство на надворешниот агол на триаголник.

Всушност, во триаголникот ABC (сл. 209) ∠1 + ∠2 = 180° - ∠3, но исто така и ∠ВСD, надворешниот агол на овој триаголник, кој не е во непосредна близина на ∠1 и ∠2, е исто така еднаков на 180° - ∠3.

Така:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Затоа, ∠1 + ∠2= ∠BCD.

Изведеното својство на надворешниот агол на триаголникот ја појаснува содржината на претходно докажаната теорема за надворешниот агол на триаголникот, во која е наведено само дека надворешниот агол на триаголникот е поголем од секој внатрешен агол на триаголник што не е во непосредна близина на него; сега е утврдено дека надворешниот агол е еднаков на збирот на двата внатрешни агли кои не се соседни со него.

3. Својство на правоаголен триаголник со агол од 30°.

Нека аголот B во правоаголниот триаголник ACB е еднаков на 30° (сл. 210). Тогаш неговиот друг остар агол ќе биде еднаков на 60 °.

Да докажеме дека кракот AC е еднаков на половина од хипотенузата AB. Да го прошириме кракот AC надвор од темето на правиот агол C и да издвоиме отсечка CM еднаква на отсечката AC. Да ја поврземе точката М со точката Б. Добиениот триаголник ВСМ е еднаков на триаголникот ACB. Гледаме дека секој агол на триаголникот ABM е еднаков на 60°, затоа овој триаголник е рамностран триаголник.

Ногата AC е еднаква на половина AM, а бидејќи AM е еднаква на AB, ногата AC ќе биде еднаква на половина од хипотенузата AB.

Збирот на внатрешните агли на триаголникот е 180 0. Ова е една од основните аксиоми на Евклидовата геометрија. Ова е геометријата што ја учат учениците. Геометријата е дефинирана како наука која ги проучува просторните форми на реалниот свет.

Што ги мотивирало античките Грци да развијат геометрија? Потребата од мерење полиња, ливади - области на земјината површина. Во исто време, античките Грци прифатиле дека површината на Земјата е хоризонтална и рамна. Земајќи ја предвид оваа претпоставка, беа создадени Евклидовите аксиоми, вклучувајќи го збирот на внатрешните агли на триаголник од 180 0.

Аксиома е предлог кој не бара доказ. Како треба да се разбере ова? Се изразува желба што му одговара на личноста, а потоа се потврдува со илустрации. Но се што не е докажано е фикција, нешто што не постои во реалноста.

Земајќи ја површината на земјата хоризонтално, старите Грци автоматски ја прифатиле формата на Земјата како рамна, но таа е поинаква - сферична. Во природата воопшто нема хоризонтални рамнини или прави линии, бидејќи гравитацијата го свиткува просторот. Прави линии и хоризонтални рамнини се наоѓаат само во човечкиот мозок.

Затоа, Евклидовата геометрија, која ги објаснува просторните форми на фиктивниот свет, е симулакрум - копија која нема оригинал.

Една од аксиомите на Евклид вели дека збирот на внатрешните агли на триаголникот е 180 0. Всушност, во вистински закривен простор, или на сферичната површина на Земјата, збирот на внатрешните агли на триаголникот е секогаш поголем од 180 0.

Ајде да размислуваме вака. Секој меридијан на земјината топка се вкрстува со екваторот под агол од 90 0. За да добиете триаголник, треба да тргнете друг меридијан подалеку од меридијанот. Збирот на аглите на триаголникот помеѓу меридијаните и страната на екваторот ќе биде 180 0. Но, сепак ќе има агол на столбот. Како резултат на тоа, збирот на сите агли ќе биде повеќе од 180 0.

Ако страните се сечат под агол од 90 0 на полот, тогаш збирот на внатрешните агли на таков триаголник ќе биде 270 0. Два меридијани кои го сечат екваторот под прав агол во овој триаголник ќе бидат паралелни еден на друг, а на полот што се сечат еден со друг под агол од 90 0 ќе станат нормални. Излегува дека две паралелни прави на иста рамнина не само што се сечат, туку можат да бидат и нормални на полот.

Се разбира, страните на таков триаголник нема да бидат прави линии, туку конвексни, повторувајќи ја сферичната форма глобус. Но, ова е токму реалниот свет на вселената.

Геометријата на реалниот простор, земајќи ја предвид неговата закривеност во средината на 19 век. развиен од германскиот математичар B. Riemann (1820-1866). Но, на учениците не им е кажано за ова.

Значи, Евклидовата геометрија, која добива форма на Земјата како рамна со хоризонтална површина, која всушност не е, е симулакрум. Ноотик е Риманова геометрија која ја зема предвид закривеноста на просторот. Збирот на внатрешните агли на триаголникот во него е поголем од 180 0.

Доказ

Нека ABC" - произволен триаголник. Да водиме низ врвот Б права паралелна со праватаА.Ц. (таква права линија се нарекува Евклидова права линија). Ајде да означиме точка на неаД така што точкитеА ИД лежеше на спротивните страни на права линија п.н.е..Агли ДБЦИ ACBеднакво како внатрешно вкрстено лежиште формирано со секант п.н.е.со паралелни линии А.Ц.И БД. Според тоа, збирот на аглите на триаголникот на темињата БИ СОеднаков на аголот ABD.Збирот на сите три агли на триаголникот е еднаков на збирот на аглите ABDИ BAC. Бидејќи овие агли се внатрешни еднострани за паралелни А.Ц.И БДна секант АБ, тогаш нивниот збир е 180°. Теоремата е докажана.

Последици

Од теоремата произлегува дека секој триаголник има два остри агли. Навистина, користејќи доказ со контрадикција, да претпоставиме дека триаголникот има само еден остар агол или воопшто нема остри агли. Тогаш овој триаголник има најмалку два агли, од кои секој е најмалку 90°. Збирот на овие агли не е помал од 180°. Но, тоа е невозможно, бидејќи збирот на сите агли на триаголникот е 180°. Q.E.D.

Генерализација во теорија на симплекс

Каде е аголот помеѓу i и j лицата на симплексот.

Белешки

• На сфера, збирот на аглите на триаголникот секогаш надминува 180 °, разликата се нарекува топчест вишок и е пропорционална со плоштината на триаголникот.
• Во рамнината на Лобачевски, збирот на аглите на триаголникот е секогаш помал од 180°. Разликата е исто така пропорционална со плоштината на триаголникот.

исто така види

Фондацијата Викимедија. 2010 година.

Погледнете што е „Теоремата за збирот на аглите на триаголникот“ во другите речници:

Својство на многуаголниците во Евклидовата геометрија: Збирот на аглите n на триаголникот е 180°(n 2). Содржина 1 Доказ 2 Забелешка ... Википедија

Питагоровата теорема е една од основните теореми на Евклидовата геометрија, која ја воспоставува врската помеѓу страните на правоаголен триаголник. Содржина 1 ... Википедија

Питагоровата теорема е една од основните теореми на Евклидовата геометрија, која ја воспоставува врската помеѓу страните на правоаголен триаголник. Содржина 1 Изјави 2 Доказ ... Википедија

Теоремата на косинус е генерализација на Питагоровата теорема. Квадратот на страната на триаголникот е еднаков на збирот на квадратите на неговите две други страни без двојно поголем производ од овие страни со косинус на аголот меѓу нив. За рамнински триаголник со страните a,b,cи агол α... ... Википедија

Овој термин има и други значења, видете Триаголник (значења). Триаголник (во Евклидов простор) е геометриска фигура, формирана од три отсечки кои поврзуваат три точки кои не лежат на иста права линија. Три точки,... ... Википедија

Стандардна нотација Триаголник е наједноставниот многуаголник со 3 темиња (агли) и 3 страни; дел од рамнината ограничен со три точки кои не лежат на иста права и три отсечки што ги поврзуваат овие точки во парови. Темиња на триаголник ... Википедија

Антички грчки математичар. Работел во Александрија во III век. п.н.е д. Главното дело „Принципија“ (15 книги), кое ги содржи основите на античката математика, елементарна геометрија, теорија на броеви, општа теоријаодноси и методи за одредување области и волумени,... ... енциклопедиски речник

- (починал помеѓу 275 и 270 г. п.н.е.) старогрчки математичар. Информациите за времето и местото на неговото раѓање не стигнале до нас, но познато е дека Евклид живеел во Александрија, а најславниот период на неговата дејност се случил за време на владеењето на Птоломеј I во Египет... ... Голем енциклопедиски речник

Геометрија слична на Евклидовата геометрија по тоа што го дефинира движењето на фигурите, но се разликува од Евклидовата геометрија по тоа што еден од нејзините пет постулати (вториот или петтиот) е заменет со негова негација. Негација на еден од Евклидовите постулати... ... Енциклопедија на Колиер

Тријаголник . Остар, тап и правоаголен триаголник.

Нозе и хипотенуза. Рамнокрак и рамностран триаголник.

Збир на агли на триаголник.

Надворешен агол на триаголник. Знаци на еднаквост на триаголници.

Впечатливи линии и точки во триаголник: висини, медијани,

симетрали, медијанад перпендикулари, ортоцентар,

центар на гравитација, центар на ограничен круг, центар на впишан круг.

Питагорова теорема. Сооднос на аспект во произволен триаголник.

Тријаголник е многуаголник со три страни (или три агли). Страните на триаголникот често се означени со мали букви што одговараат на големите букви што ги претставуваат спротивните темиња.

Ако сите три агли се остри (сл. 20), тогаш ова акутен триаголник . Ако еден од аглите е прав(В, Сл.21), тоа е правоаголен триаголник; страниа, бформирање прав агол се нарекуваат нозете; странавспроти прав агол се вика хипотенуза. Доколку еден одтапи агли (Б, Сл. 22), тоа е тап триаголник.


Триаголник ABC (слика 23) - рамнокрак, Ако дванеговите страни се еднакви (а= в); се нарекуваат овие еднакви страни странично, се нарекува трето лице основатријаголник. Тријаголник ABC (Слика 24) - рамностран, Ако Ситенеговите страни се еднакви (а = б = в). Генерално ( а ≠ б ≠ в) ние имаме скалентријаголник .

Основни својства на триаголниците. Во кој било триаголник:

1. Наспроти поголемата страна лежи поголемиот агол, и обратно.

2. Еднакви агли лежат спроти еднакви страни, и обратно.

Особено, сите агли во рамнострантриаголникот се еднакви.

3. Збирот на аглите на триаголникот е 180 º .

Од последните две својства произлегува дека секој агол во рамностран

триаголникот е 60 º.

4. Продолжувајќи една од страните на триаголникот (AC, Сл. 25), добиваме надворешен

агол BCD . Надворешниот агол на триаголникот е еднаков на збирот на внатрешните агли,

не во непосредна близина на него : BCD = A + B.

5. Било кој страната на триаголникот е помала од збирот на другите две страни и поголема

нивните разлики (а < б + в, а > б – в;б < а + в, б > а – в;в < а + б,в > а – б).

Знаци на еднаквост на триаголници.

Триаголниците се складни ако се соодветно еднакви:

а ) две страни и аголот меѓу нив;

б ) два агли и страната соседна до нив;

в) три страни.

Знаци на еднаквост на правоаголните триаголници.

Две правоаголнатриаголниците се еднакви ако е исполнет еден од следниве услови:

1) нивните нозе се еднакви;

2) кракот и хипотенузата на едниот триаголник се еднакви на кракот и хипотенузата на другиот;

3) хипотенузата и акутниот агол на едниот триаголник се еднакви на хипотенузата и акутниот агол на другиот;

4) кракот и соседниот остар агол на едниот триаголник се еднакви на кракот и соседниот остар агол на другиот;

5) кракот и спротивниот остар агол на еден триаголник се еднакви на кракот и спротивниот остар агол на другиот.

Прекрасни линии и точки во триаголникот.

Висина триаголникот енормално,спуштен од кое било теме на спротивната страна ( или негово продолжение). Оваа страна се нарекуваосновата на триаголникот . Трите височини на триаголникот секогаш се сечатво еден момент, повикан ортоцентартријаголник. Ортоцентар на акутен триаголник (точкаО , Сл. 26) се наоѓа во внатрешноста на триаголникот иортоцентар на тап триаголник (точкаО , сл.27) – надвор; Ортоцентарот на правоаголен триаголник се совпаѓа со темето на правиот агол.

Медијана - Ова линиски сегмент , поврзувајќи го секое теме на триаголник со средината на спротивната страна. Три средни на триаголник (AD, BE, CF, сл.28) се вкрстуваат во една точка О , секогаш лежи внатре во триаголникоти да се биде негов Центар на гравитација. Оваа точка ја дели секоја медијана во сооднос 2:1, сметајќи од темето.

Симетрала - Ова симетрала сегментагол од теме до точка раскрсници со спротивната страна. Три симетрали на триаголник (AD, BE, CF, сл.29) се вкрстуваат во една точка О, секогаш лежи внатре во триаголникотИ битие центарот на впишаниот круг(види дел „Впишанои ограничени многуаголници“).

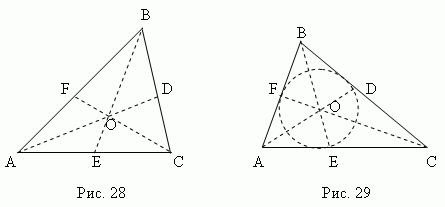
Симетралата ја дели спротивната страна на делови пропорционални на соседните страни ; на пример, на Сл. 29 AE: CE = AB: п.н.е.

Медијана нормална е нормална извлечена од срединатасегментни точки (страни). Три нормални симетрали на триаголникот ABC(КО, МО, НЕ, Сл. 30 ) се сечат во една точка О, што е центар ограничен круг (точки К, М, Н – средните точки на страните на триаголникот ABC).

Во акутен триаголник, оваа точка лежи внатре во триаголникот; во тап - надвор; во правоаголна - во средината на хипотенузата. Ортоцентар, центар на гравитација, обиколница и впишан круг се совпаѓаат само во рамностран триаголник.

Питагорова теорема. Во правоаголен триаголник, квадрат со должинаХипотенузата е еднаква на збирот на квадратите на должината на краците.

Доказот за Питагоровата теорема јасно следи од Сл. 31. Размислете за правоаголен триаголник ABC со нозе а, би хипотенуза в.

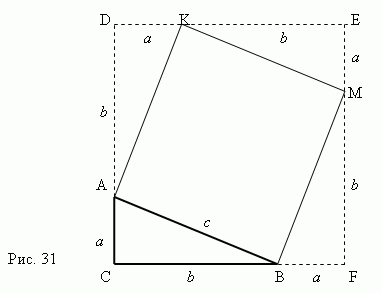
Ајде да изградиме плоштадАКМБ користејќи ја хипотенузатаАБ како страна. Потоапродолжи со страните на правоаголен триаголник ABC за да се добие квадрат CDEF , чија страна е еднакваa + b .Сега е јасно дека површината на плоштадот CDEF е еднаков на ( a+b) 2 . Од друга страна, ова површина е еднаква на збиротобласти четири правоаголни триаголниции плоштадот АКМБ т.е

в 2 + 4 (ab / 2) = в 2 + 2 ab,

од тука,

в 2 + 2 ab= (a+b) 2 ,

и конечно имаме:

в 2 =а 2 +б 2 .

Сооднос на аспект во произволен триаголник.

Во општиот случај (за произволен триаголник) имаме:

в 2 =а 2 +б 2 – 2ab· cos В,

каде што Ц – агол помеѓу странитеаИ б .