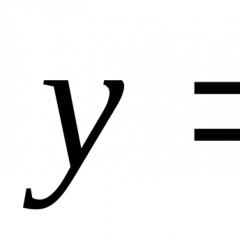Формула за пресметување на волумените на телата на револуцијата. Како да се пресмета волуменот на телото на револуција користејќи дефинитивен интеграл? Областа на рамна фигура

Дефиниција 3. Тело на револуција е тело добиено со ротирање на рамна фигура околу оската што не ја пресекува фигурата и лежи во иста рамнина со неа.

Оската на ротација може да ја пресече фигурата ако е оската на симетрија на фигурата.

Теорема 2.
, оска
и прави сегменти
И

ротира околу една оска
. Тогаш волуменот на добиеното тело на ротација може да се пресмета со помош на формулата

(2)

Доказ. За такво тело, пресекот со апсциса е круг со радиус
, Средства
а формулата (1) го дава бараниот резултат.

Ако фигурата е ограничена со графиконите на две континуирани функции
И
, и линиски отсечки
И
, и
И
, потоа при ротација околу оската x добиваме тело чиј волумен

Пример 3. Пресметајте го волуменот на торусот добиен со ротирање на круг ограничен со круг

околу оската на апсцисата.

Р одлука. Посочениот круг е ограничен подолу со графикот на функцијата
и одозгора -
. Разликата на квадратите на овие функции:

Потребен волумен

(графикот на интеграндот е горниот полукруг, така што интегралот напишан погоре е плоштината на полукругот).

Пример 4. Параболичен сегмент со основа
, и висина , се ротира околу основата. Пресметајте го волуменот на добиеното тело („лимон“ од Кавалиери).

Р одлука. Ќе ја поставиме параболата како што е прикажано на сликата. Потоа нејзината равенка
, и
. Ајде да ја најдеме вредноста на параметарот :
. Значи, потребниот волумен:

Теорема 3. Нека криволинеарен трапез е ограничен со графикот на континуирана ненегативна функција
, оска
и прави сегменти
И
, и
, ротира околу оска
. Тогаш волуменот на добиеното тело на ротација може да се најде со формулата

(3)

Идејата за докажување. Ние го делиме сегментот
точки

, на делови и нацртајте прави линии
. Целиот трапез ќе се распадне на ленти, кои може да се сметаат за приближно правоаголници со основа
и висина
.

Добиениот цилиндар го отсекуваме со ротирање на таков правоаголник долж неговата генератрикс и го расклопуваме. Добиваме „речиси“ паралелепипед со димензии:
,
И
. Неговиот волумен
. Значи, за волуменот на телото на револуција ќе имаме приближна еднаквост

За да се добие точна еднаквост, мора да се оди до границата во
. Збирот напишан погоре е интегрален збир за функцијата
, значи, во лимитот го добиваме интегралот од формулата (3). Теоремата е докажана.

Забелешка 1. Во теоремите 2 и 3 условот
може да се изостави: формулата (2) е генерално нечувствителна на знакот
, а во формулата (3) е доволно
заменет со
.

Пример 5. Параболичен сегмент (основа
, висина ) ротира околу висината. Најдете го волуменот на добиеното тело.

Решение. Да ја поставиме параболата како што е прикажано на сликата. И иако оската на ротација ја пресекува фигурата, таа - оската - е оската на симетрија. Затоа, треба да ја разгледаме само десната половина од сегментот. Равенка на парабола
, и
, Средства
. За волумен имаме:

Забелешка 2. Ако криволинеарната граница на криволинеарен трапез е дадена со параметарски равенки
,
,
И
,
тогаш можете да ги користите формулите (2) и (3) со замена на
И
на
кога се менува тод
пред .

Пример 6. Бројката е ограничена со првиот лак на циклоидот
,
,
, и x-оската. Најдете го волуменот на телото добиен со ротирање на оваа бројка околу: 1) оска
; 2) оски
.

Решение. 1) Општа формула
Во нашиот случај:

2) Општа формула
За нашата фигура:

Ги покануваме студентите сами да ги спроведат сите пресметки.

Забелешка 3. Нека закривен сектор ограничен со континуирана линија
и зраци
,

, ротира околу поларна оска. Волуменот на добиеното тело може да се пресмета со помош на формулата.

Пример 7. Дел од фигура ограничена со кардиоид
, лежејќи надвор од кругот
, ротира околу поларна оска. Најдете го волуменот на добиеното тело.

Решение. Двете линии, а со тоа и фигурата што ја ограничуваат, се симетрични во однос на поларната оска. Затоа, потребно е да се разгледа само оној дел за кој
. Кривите се сечат на
И

на
. Понатаму, бројката може да се смета како разлика на два сектори, и затоа волуменот може да се пресмета како разлика на два интеграли. Ние имаме:

Задачи за самостојна одлука.

1. Кружен сегмент чија основа
, висина , се ротира околу основата. Најдете го волуменот на телото на револуцијата.

2. Најдете го волуменот на параболоид на револуција чија основа , а висината е .

3. Фигура ограничена со астроид
,
ротира околу оската на апсцисата. Најдете го волуменот на добиеното тело.

4. Слика ограничена со линии
И
ротира околу оската x. Најдете го волуменот на телото на револуцијата.

Тема: „Пресметување на волумените на телата на револуција со помош на определен интеграл“

Тип на лекција:комбинирано.

Целта на лекцијата:Научете да ги пресметувате волумените на телата на револуција користејќи интеграли.

Задачи:

консолидирање на способноста да се идентификуваат криволинеарни трапезоиди од голем број геометриски фигури и развивање на вештината за пресметување на областите на криволинеарни трапезоиди;

да се запознаат со концептот на тридимензионална фигура;

научи да ги пресметува волумените на телата на револуцијата;

промовирање на развојот на логично размислување, компетентен математички говор, точност при конструирање цртежи;

да негува интерес за предметот, да работи со математички поими и слики, да негува волја, независност и истрајност во постигнувањето на конечниот резултат.

За време на часовите

I. Организациски момент.

Поздрав од групата. Пренеси им ги целите на часот на учениците.

Би сакал да ја започнам денешната лекција со парабола. „Еднаш одамна живееше еден мудар човек кој знаеше сè. Еден човек сакаше да докаже дека мудрецот не знае сè. Држејќи пеперутка во дланките, праша: „Кажи ми, мудрец, која пеперутка е во моите раце: жива или мртва?“ И тој мисли: „Ако живата рече, ќе ја убијам; ако рече мртвиот, ќе ја ослободам“. Мудрецот, откако размислил, одговорил: „Сè е во ваши раце“.

Затоа, да работиме плодно денес, да стекнеме нова залиха на знаење, а стекнатите вештини и способности ќе ги примениме во идниот живот и во практичните активности. „Се е во ваши раце“.

II. Повторување на претходно проучен материјал.

Ајде да се потсетиме на главните точки на претходно изучениот материјал. За да го направите ова, ајде да ја завршиме задачата „Елиминирајте го дополнителниот збор“.

(Учениците кажуваат дополнителен збор.)

Во право „Диференцијал“.Обидете се да ги именувате преостанатите зборови со еден заеднички збор. (Интегрална пресметка.)

Да се потсетиме на главните фази и концепти поврзани со интегралната пресметка.

Вежбајте.Повратете ги празнините. (Ученикот излегува и ги запишува бараните зборови со маркер.)

Работете во тетратки.

Формулата Њутн-Лајбниц ја изведоа англискиот физичар Исак Њутн (1643-1727) и германскиот филозоф Готфрид Лајбниц (1646-1716). И тоа не е изненадувачки, бидејќи математиката е јазикот што го зборува самата природа.

Ајде да размислиме како оваа формула се користи за решавање на практични проблеми.

Пример 1: Пресметајте ја плоштината на фигурата ограничена со линии

Решение:Ајде да конструираме графикони на функции на координатната рамнина . Ајде да ја избереме областа на фигурата што треба да се најде.

III. Учење нов материјал.

Обрнете внимание на екранот. Што е прикажано на првата слика? (Сликата покажува рамна фигура.)

Што е прикажано на втората слика? Дали оваа бројка е рамна? (Сликата покажува тродимензионална фигура.)

Во вселената, на земјата и во секојдневниот живот не се среќаваме само со рамни фигури, туку и со тридимензионални, но како да го пресметаме волуменот на таквите тела? На пример: волумен на планета, комета, метеорит итн.

Луѓето размислуваат за волуменот и кога градат куќи и кога истураат вода од еден сад во друг. Требаше да се појават правила и техники за пресметување на волумени, а колку се точни и оправдани е друго прашање.

1612 година била многу плодна за жителите на австрискиот град Линц, каде што живеел познатиот астроном Јоханес Кеплер, особено за грозје. Луѓето подготвуваа буриња со вино и сакаа да знаат како практично да ги одредат нивните волумени.

Така, разгледуваните дела на Кеплер го означија почетокот на цела фреквенција на истражување што кулминираше во последната четвртина од 17 век. дизајн во делата на I. Newton и G.V. Лајбниц на диференцијално и интегрално сметање. Од тоа време, математиката на променливи зазема водечко место во системот на математичко знаење.

Денес вие и јас ќе се вклучиме во такви практични активности, затоа,

Темата на нашата лекција: „Пресметување на волумените на телата на ротација користејќи дефинитивен интеграл“.

Дефиницијата за тело на револуција ќе ја научите со завршување на следната задача.

„Лавиринт“.

Вежбајте.Најдете излез од збунувачката ситуација и запишете ја дефиницијата.

IVПресметка на волумени.

Користејќи дефинитивен интеграл, можете да го пресметате волуменот на одредено тело, особено телото на ротација.

Тело на вртење е тело добиено со ротирање на заоблен трапез околу неговата основа (сл. 1, 2)

Волуменот на телото на револуција се пресметува со помош на една од формулите:

1. околу оската OX.

2. , ако ротацијата на закривен трапез околу оската на оп-засилувачот.

Учениците ги запишуваат основните формули во тетратка.

Наставникот ги објаснува решенијата на примерите на табла.

1. Најдете го волуменот на телото добиен со ротирање околу ординатна оска на криволинеарен трапез ограничен со линии: x2 + y2 = 64, y = -5, y = 5, x = 0.

Решение.

Одговор: 1163 cm3.

2. Најдете го волуменот на телото добиен со ротирање на параболичен трапез околу оската x y = , x = 4, y = 0.

Решение.

В. Математички симулатор.

2. Се вика множеството од сите антидеривати на дадена функција

А) неопределен интеграл,

Б) функција,

Б) диференцијација.

7. Најдете го волуменот на телото добиен со ротирање околу оската на апсцисата на криволинеарен трапез ограничен со линии:

Д/З. Консолидирање на нов материјал

Пресметајте го волуменот на телото формирано со ротација на ливчето околу оската x y = x2, y2 = x.

Ајде да изградиме графикони на функцијата. y = x2, y2 = x. Да го трансформираме графикот y2 = x во форма y = .

Имаме V = V1 - V2 Да го пресметаме волуменот на секоја функција:

Заклучок:

Дефинитивниот интеграл е одредена основа за изучување на математиката, која дава незаменлив придонес во решавањето на практичните проблеми.

Темата „Интеграл“ јасно ја демонстрира врската помеѓу математиката и физиката, биологијата, економијата и технологијата.

Развојот на модерната наука е незамислив без употреба на интегралот. Во овој поглед, неопходно е да се започне со изучување во рамките на средното специјализирано образование!

VI. Оценување.(Со коментар.)

Големиот Омар Кајам - математичар, поет, филозоф. Тој нè поттикнува да бидеме господари на сопствената судбина. Да слушнеме извадок од неговото дело:

Велиш, овој живот е еден момент.
Ценете го, црпете инспирација од него.
Како го трошиш, така ќе помине.
Не заборавајте: таа е ваша креација.

Користење на интеграли за пронаоѓање на волумените на телата на револуцијата

Практичната корисност на математиката се должи на фактот што без

Специфичното математичко знаење го отежнува разбирањето на принципите на уредот и употребата на модерната технологија. Секој човек во својот живот мора да изврши доста сложени пресметки, да користи најчесто користена опрема, да ги најде потребните формули во референтните книги и да создава едноставни алгоритми за решавање проблеми. Во современото општество, сè повеќе специјалности кои бараат високо ниво на образование се поврзани со директна примена на математиката. Така, математиката станува професионално значаен предмет за студентот. Водечката улога и припаѓа на математиката во формирањето на алгоритамското размислување, таа развива способност да дејствува според даден алгоритам и да конструира нови алгоритми.

Додека ја проучувам темата за користење на интегралот за пресметување на волумените на телата на револуцијата, предлагам учениците во изборните часови да ја разгледаат темата: „Волумени на тела на револуција користејќи интеграли“. Подолу се дадени методолошки препораки за разгледување на оваа тема:

1. Површина на рамна фигура.

Од курсот за алгебра знаеме дека проблемите од практична природа доведоа до концептот на определен интеграл..gif" width="88" height="51">.jpg" width="526" height="262 src=" >

https://pandia.ru/text/77/502/images/image006_95.gif" width="127" height="25 src=">.

За да се најде волуменот на телото на ротација формирано со ротација на криволинеарен трапез околу оската Ox, ограничен со прекината линија y=f(x), оската Ox, правите x=a и x=b, пресметуваме користејќи ја формулата

https://pandia.ru/text/77/502/images/image008_26.jpg" width="352" height="283 src=">Y

3.Волумен на цилиндарот.

https://pandia.ru/text/77/502/images/image011_58.gif" width="85" height="51">..gif" width="13" height="25">..jpg" width="401" height="355">Конусот се добива со ротирање на правоаголен триаголник ABC (C = 90) околу оската Ox на која лежи кракот AC.

Сегментот AB лежи на правата линија y=kx+c, каде што https://pandia.ru/text/77/502/images/image019_33.gif" width="59" height="41 src=">.

Нека a=0, b=H (H е висината на конусот), тогаш Vhttps://pandia.ru/text/77/502/images/image021_27.gif" width="13" height="23 src= ">.

5.Волумен на скратен конус.

Скратен конус може да се добие со ротирање на правоаголен трапез ABCD (CDOx) околу оската Ox.

Отсечката AB лежи на правата y=kx+c, каде , c=r.

Бидејќи правата линија минува низ точката А (0;r).

Така, правата линија изгледа како https://pandia.ru/text/77/502/images/image027_17.gif" width="303" height="291 src=">

Нека a=0, b=H (H е висината на скратениот конус), потоа https://pandia.ru/text/77/502/images/image030_16.gif" width="36" height="17 src ="> = .

6. Волумен на топката.

Топката може да се добие со ротирање на круг со центар (0;0) околу оската Ox. Полукругот кој се наоѓа над оската Ox е даден со равенката

https://pandia.ru/text/77/502/images/image034_13.gif" width="13" height="16 src=">x Р.

Тип на лекција: комбиниран.

Целта на лекцијата:Научете да ги пресметувате волумените на телата на револуција користејќи интеграли.

Задачи:

консолидирање на способноста да се идентификуваат криволинеарни трапезоиди од голем број геометриски фигури и развивање на вештината за пресметување на областите на криволинеарни трапезоиди;
да се запознаат со концептот на тридимензионална фигура;
научи да ги пресметува волумените на телата на револуцијата;
промовирање на развојот на логично размислување, компетентен математички говор, точност при конструирање цртежи;
да негува интерес за предметот, да работи со математички поими и слики, да негува волја, независност и истрајност во постигнувањето на конечниот резултат.

За време на часовите

I. Организациски момент.

Поздрав од групата. Пренеси им ги целите на часот на учениците.

Рефлексија. Мирна мелодија.

– Би сакал да ја започнам денешната лекција со парабола. „Еднаш одамна живееше еден мудар човек кој знаеше сè. Еден човек сакаше да докаже дека мудрецот не знае сè. Држејќи пеперутка во дланките, праша: „Кажи ми, мудрец, која пеперутка е во моите раце: жива или мртва?“ А тој самиот мисли: „Ако живата рече, ќе ја убијам, мртвиот ќе рече, ќе ја ослободам“. Мудрецот, откако размислил, одговорил: „Сè во ваши раце“. (Презентација.Слајд)

– Затоа, денес да работиме плодно, да стекнеме нова залиха на знаење, а стекнатите вештини и способности ќе ги применуваме во идниот живот и во практичните активности. „Сè во ваши раце“.

II. Повторување на претходно проучен материјал.

– Да се потсетиме на главните точки од претходно изучениот материјал. За да го направите ова, ајде да ја завршиме задачата „Елиминирајте го дополнителниот збор“.(Слајд.)

(Ученикот оди во И.Д. користи гума за бришење за да го отстрани дополнителниот збор.)

- Точно „Диференцијал“. Обидете се да ги именувате преостанатите зборови со еден заеднички збор. (Интегрална пресметка.)

– Да се потсетиме на главните фази и концепти поврзани со интегралната пресметка..

„Математички куп“.

Вежбајте. Повратете ги празнините. (Ученикот излегува и ги запишува бараните зборови со пенкало.)

– Апстракт за примената на интегралите ќе слушнеме подоцна.

Работете во тетратки.

– Формулата Њутн-Лајбниц ја изведоа англискиот физичар Исак Њутн (1643–1727) и германскиот филозоф Готфрид Лајбниц (1646–1716). И тоа не е изненадувачки, бидејќи математиката е јазикот што го зборува самата природа.

– Да разгледаме како оваа формула се користи за решавање на практични проблеми.

Пример 1: Пресметајте ја плоштината на фигурата ограничена со линии

Решение: Да изградиме графикони на функции на координатната рамнина . Ајде да ја избереме областа на фигурата што треба да се најде.

III. Учење нов материјал.

– Обрнете внимание на екранот. Што е прикажано на првата слика? (Слајд) (Сликата покажува рамна фигура.)

– Што е прикажано на втората слика? Дали оваа бројка е рамна? (Слајд) (Сликата покажува тродимензионална фигура.)

– Во вселената, на земјата и во секојдневниот живот не се среќаваме само со рамни фигури, туку и со тродимензионални, но како да го пресметаме волуменот на таквите тела? На пример, обемот на планета, комета, метеорит итн.

– Луѓето размислуваат за волуменот и кога градат куќи и кога истураат вода од еден сад во друг. Требаше да се појават правила и техники за пресметување на волумените; колку тие беа точни и разумни е друго прашање.

Порака од студент. (Тјурина Вера.)

– Така, разгледуваните дела на Кеплер ги поставија темелите за цел тек на истражување што кулминираше во последната четвртина од 17 век. дизајн во делата на I. Newton и G.V. Лајбниц на диференцијално и интегрално сметање. Од тоа време, математиката на променливи зазема водечко место во системот на математичко знаење.

– Денеска вие и јас ќе се вклучиме во вакви практични активности, затоа,

Темата на нашата лекција: „Пресметување на волумените на телата на ротација користејќи дефинитивен интеграл“. (Слајд)

– Дефиницијата за тело на ротација ќе ја научите со завршување на следната задача.

„Лавиринт“.

Лавиринт (грчки збор) значи одење под земја. Лавиринт е сложена мрежа од патеки, премини и простории кои се поврзуваат.

Но, дефиницијата беше „скршена“, оставајќи индиции во форма на стрели.

Вежбајте. Најдете излез од збунувачката ситуација и запишете ја дефиницијата.

Слајд. „Упатство за мапа“ Пресметка на волумени.

Тело на вртење е тело добиено со ротирање на заоблен трапез околу неговата основа (сл. 1, 2)

Волуменот на телото на ротација се пресметува со помош на една од формулите:

1. околу оската OX.

2. , ако ротацијата на закривен трапез околу оската на оп-засилувачот.

Секој ученик добива наставна картичка. Наставникот ги нагласува главните точки.

– Наставникот ги објаснува решенијата на примерите на табла.

Ајде да разгледаме извадок од познатата бајка на А. (Слајд 4):

…..
И пијаниот гласник донесе
Истиот ден редоследот е како што следува:
„Кралот им наредува на своите болјари,
Без губење време,
И кралицата и потомството
Тајно фрли во бездната на водата“.
Нема што да се прави: момчиња,
Загриженост за суверенот
И на младата кралица,
Во нејзината спална соба дојде толпа луѓе.
Тие ја објавија волјата на кралот -
Таа и нејзиниот син имаат злобен дел,
Го читавме декретот на глас,
И кралицата во истиот час
Ме ставија во буре со син ми,
Направија катран и се оддалечија
И ме пуштија во окијан -
Така нареди цар Салтан.

Колкав треба да биде волуменот на бурето за да може да се сместат кралицата и нејзиниот син во него?

– Размислете за следните задачи

1. Најдете го волуменот на телото добиен со ротирање околу ординатна оска на криволинеарен трапез ограничен со линии: x 2 + y 2 = 64, y = -5, y = 5, x = 0.

Одговор: 1163 цм 3 .

Најдете го волуменот на телото добиен со ротирање параболичен трапез околу оската на апсцисата y = , x = 4, y = 0.

IV. Консолидирање на нов материјал

Пример 2. Пресметајте го волуменот на телото формиран од ротацијата на ливчето околу оската x y = x 2, y 2 = x.

Ајде да изградиме графикони на функцијата. y = x 2, y 2 = x. Распоред y2 = xконвертирате во формата y= .

Ние имаме V = V 1 – V 2Ајде да го пресметаме обемот на секоја функција

– Сега, да ја погледнеме кулата за радио станицата во Москва на Шаболовка, изградена според дизајнот на извонредниот руски инженер, почесен академик В. Г. Шухов. Се состои од делови - хиперболоиди на ротација. Покрај тоа, секој од нив е направен од директни метални шипки што ги поврзуваат соседните кругови (слика 8, 9).

- Да го разгледаме проблемот.

Најдете го волуменот на телото добиен со ротирање на хиперболните лаци околу неговата имагинарна оска, како што е прикажано на сл. 8, каде

коцка единици

Групни задачи. Учениците влечат ждрепка со задачи, цртаат цртежи на хартија Whatman, а еден од претставниците на групата ја брани работата.

1 група.

Удри! Удри! Уште еден удар!
Топката лета во голот - ТОПКА!
И ова е топче од лубеница
Зелена, тркалезна, вкусна.
Погледнете подобро - каква топка!
Тој е направен од ништо друго освен кругови.
Исечете ја лубеницата на кругови
И вкусете ги.

Најдете го волуменот на телото добиен со ротација околу оската OX на функцијата ограничена

Грешка! Обележувачот не е дефиниран.

– Те молам кажи ми каде ја среќаваме оваа бројка?

Куќа. задача за 1 група. ЦИЛИНДАР (слајд) .

"Цилиндар - што е тоа?" – го прашав татко ми.
Таткото се насмеа: Горниот шешир е капа.
За да имате правилна идеја,
Цилиндар, да речеме, е лимена конзерва.
Цевка за пароброд - цилиндар,
И цевката на нашиот покрив,

Сите цевки се слични на цилиндар.
И дадов ваков пример -
Мој сакан калеидоскоп,
Не можете да го тргнете погледот од него,
И, исто така, изгледа како цилиндар.

- Вежбајте. Домашна задача: графика на функцијата и пресметување на јачината на звукот.

2-ра група. КОНСКИ (слајд).

Мама рече: И сега
Мојата приказна ќе биде за конусот.
Stargazer во висока капа
Ги брои ѕвездите во текот на целата година.
КОНСКИ - капа на ѕвездениот поглед.
Таков е тој. Разбрав? Тоа е тоа.
Мама стоеше на масата,
Истурив масло во шишиња.
-Каде е инката? Нема инка.
Побарајте го. Не стојте на страна.
- Мамо, нема да попуштам.
Кажете ни повеќе за конусот.
– Инката е во форма на конус за полевање.
Ајде, најди ми ја брзо.
Не можев да ја најдам инката
Но, мама направи торба,
Го завиткав картонот околу прстот
И таа вешто го прицврсти со спојка за хартија.
Маслото тече, мама е среќна,
Конусот излезе точно.

Вежбајте. Пресметај го волуменот на телото добиен со ротирање околу оската на апсцисата

Куќа. задача за 2 група. ПИРАМИДА(слајд).

Ја видов сликата. На оваа слика
Во песочната пустина има ПИРАМИДА.
Сè во пирамидата е извонредно,
Во него има некаква мистерија и мистерија.
И кулата Спаскаја на Црвениот плоштад
Тоа е многу познато и за децата и за возрасните.
Ако ја погледнете кулата, изгледа обично,
Што има на врвот на тоа? Пирамида!

Вежбајте.Домашна задача: графика на функцијата и пресметување на волуменот на пирамидата

– Волумените на различни тела ги пресметавме врз основа на основната формула за волумени на телата со помош на интеграл.

Ова е уште една потврда дека дефинитивниот интеграл е некаква основа за изучување на математиката.

- Па, сега да се одмориме малку.

Најдете пар.

Свири математичка домино мелодија.

„Патот што јас самиот го барав никогаш нема да биде заборавен...“

Истражувачка работа. Примена на интегралот во економијата и технологијата.

Тестови за силни ученици и математички фудбал.

Математички симулатор.

2. Се вика множеството од сите антидеривати на дадена функција

А) неопределен интеграл,

Б) функција,

Б) диференцијација.

Д/З. Пресметајте ги волумените на телата на револуцијата.

Рефлексија.

Прием на рефлексија во форма синхронизираат(пет реда).

1. ред – име на тема (една именка).

2 ред – опис на темата со два збора, две придавки.

3 ред – опис на дејството во оваа тема во три збора.

Четвртиот ред е фраза од четири збора што го покажува односот кон темата (цела реченица).

Петтиот ред е синоним кој ја повторува суштината на темата.

Волумен.
Дефинитивна интегрална, интеграбилна функција.
Градиме, ротираме, пресметуваме.
Тело добиено со ротирање на заоблен трапез (околу неговата основа).
Тело на ротација (волуметриско геометриско тело).

Заклучок (слајд).

Дефинитивен интеграл е одредена основа за изучување на математиката, која дава незаменлив придонес во решавањето на практичните проблеми.
Темата „Интеграл“ јасно ја демонстрира врската помеѓу математиката и физиката, биологијата, економијата и технологијата.
Развојот на модерната наука е незамислив без употреба на интегралот. Во овој поглед, неопходно е да се започне со изучување во рамките на средното специјализирано образование!

Оценување. (Со коментар.)

Ќе речете, овој живот е еден момент.
Ценете го, црпете инспирација од него.
Како го трошиш, така ќе помине.
Не заборавајте: таа е ваша креација.