Практичен час „пресметка на деривати“. Практичен час „пресметување изводи“ Најдете го изводот на функцијата y
Цели на лекцијата:
Образовни- знае формули за диференцијација; правила за диференцијација;
диференцијација на сложена функција; физичко и геометриско значење на дериватот;
равенка на тангента на графикот на функција.
Развојна -да може да најде изводи на функции; решава проблеми користејќи физичко значење, геометриско значење; најдете ја вредноста на изводот на функцијата во точка; математички правилно да ги објасни и оправда извршените дејствија.
Образовни -негувајте независност, одговорност, размислување.
За време на часовите
I. Организациски момент.
II. Проверка на домашната задача
(за време на паузите, консултантите проверуваат (учениците) и доделуваат оценки).
III. Поставување цели и мотивација
Наставникот ги информира учениците дека овој час е последниот час на тема „Пресметување деривати“ и ги повикува да формулираат сопствени цели.
Учител: „Големиот филозоф Конфучие еднаш рекол: „Три патишта водат до знаење: патот на размислувањето е најблагородниот пат, патот на имитацијата е најлесниот пат, а патот на искуството е најгорчливиот пат“. Така, денес на час, секој од вас ќе одреди по кој пат до знаење за оваа тема е“.
Учениците добиваат задача да ги покажат своите знаења и вештини за пресметување на деривати и добиваат план за час.
Фаза I:Завршување на задачата со помош на картичката „Запомни“.
(проверка на знаење за формули и правила на диференцијација).
Фаза II:Усна фронтална работа на повторување и генерализирање на знаењата.
Фаза III:„Прогноза за тестирање“ (при извршување на оваа задача, помошта од консултанти е прифатлива).
ЈасФаза V:Решение на практичен проблем.
Фаза V:Самостојна работа
Се оценуваат фазите I, III, V од работа и домашна задача. Консултантите ги проверуваат и ги внесуваат резултатите во табелата за оценување.
Критериум за оценување: "5"- 19-20 поени;
"4"- 15-18 поени;
"3"- 10-14 поени.
Патишта до знаење
- Репродукција и корекција на референтни знаења
Фаза I.
Цел:контрола, самоконтрола на познавање на формули и правила на диференцијација
Запомнете! Ф.И. _________________________________________________ |
|
Дериват |
|
в, в - минуси т |
|
|
|
|
|
ѓ„(x)+ е"(x) |
|
ѓ(x)* е(x) |
|
|
|
На крајот од оваа задача, се врши само-тестирање со помош на „Табела на деривати“. Картичките се предаваат на консултанти за проверка (корекциите на картичките не се дозволени).
V. Генерализација и систематизација на знаењето
Фаза II.
1. Усна фронтална работа.
А.Создадете задача за оваа состојба и решете ја.
![]()
1. Најдете ја вредноста на изводот на функцијата во точката t = 3. (Одговор: 21.)
2. Направете равенка за тангентата на графикот на функцијата во точката t = 3. (Одговор: y = 21x-45.).
3. Најдете ја брзината на телото и забрзувањето во моментот t=3c, ако законот на движење е даден со формулата. (Одговор: 21 m/s, 16 m/s²).
4. Најдете го аголниот коефициент на тангентата нацртана на графикот на функцијата во точката t = 3. (Одговор: 21.).
5. Најдете ја тангентата на аголот на наклонетост на тангентата на графикот на функцијата во точката t = 3 и определи го типот на аголот помеѓу тангентата и позитивната насока на оската Ox. (Одговор: tgα, аголот α е остар)
Б. Најдете изводи на функции

2. Фаза III„Прогноза за тестирање“


На крајот од оваа задача се врши самотестирање врз основа на конечните одговори и тестовите се предаваат на консултанти. (не се дозволени корекции на картичките).
Одговори:
1 опција |
||||
Опција 2 |
- Решението на проблемот
ЈасФаза V
Фронтално решение на проблем на напредно ниво (решението го вршат консултанти заедно со класот).
Задача
На кои параметри вредности атангенти на графикот на функцијата ![]()
нацртани на точките на неговото пресекување со оската X, формираат агол од 60° меѓу себе?

Графикот е парабола со нагорни гранки кои ја сечат оската X во две точки (случајот а=0 не го задоволува значењето на проблемот):
IX. Сумирање и оценување
1. Прашања: а) Дали е постигната целта на часот?
б) Која фаза изгледаше најтешка?
в) Што беше најинтересно?
2. Консултантите ги објавуваат резултатите (број и имиња на студенти на пат
имитација, начини на размислување и начини на искуство).
Практична работа
математика
1. Наоѓање на граница на функција. Првиот и вториот се прекрасни граници.
2. Извод на сложена функција. Проучување на функција на една променлива и исцртување графикони.
3. Тест „Примена на диференцијална пресметка за проучување на функциите“.
4. Наоѓање на неопределени интеграли. Пресметка на определени интеграли.
5. Пресметка на детерминанти.
6. Решавање системи на линеарни равенки со помош на Крамеровиот метод. Тест.
7. Решавање проблеми на тема „Метали“. Формули за логичка алгебра.
8. Пресметка на веројатности на случајни настани. Формула за вкупна веројатност.
9. Пресметка на нумерички карактеристики.
10. Тест „Основи на теоријата на веројатност и математичка статистика“
11. Тригонометриска форма на комплексен број.
12. Дејства со сложени броеви во различни форми.
МЕТОДОЛОШКИ УПАТСТВА ЗА ПРАКТИЧНА РАБОТА ПО МАТЕМАТИКА
КУРС 2
Практичниот час е форма на организирање на образовниот процес, кој вклучува ученици кои изведуваат една или повеќе практични работи по задача и под водство на наставник.
Така, на практичната настава по математика кај учениците се развива способност за решавање проблеми, кои во иднина треба да се користат за решавање на стручни проблеми во посебни дисциплини.
Во текот на практичната работа, студентите ја совладаат способноста да користат извори на информации, да работат со регулаторни документи и наставни материјали, референтни книги, да прават цртежи, дијаграми, табели, да решаваат разни проблеми и да прават пресметки.
Проблеми што се решаваат за време на практичните часови по математика:
1) проширување и консолидација на теоретските знаења по математика стекнати за време на предавањата;
2) развивање кај учениците практични вештини и способности неопходни за успешно решавање на проблемите по математика;
3) развивање на потребата на учениците за самообразование и усовршување на знаењата и вештините во процесот на изучување математика;
4) формирање на креативен став и истражувачки пристап во процесот на изучување на математиката;
5) формирање на професионално значајни квалитети на иден специјалист и вештини за примена на стекнатото знаење во професионалната област.
Практичен час бр. 1.Пресметка на границите на функцијата. Првиот и вториот се прекрасни граници.
Предмет : Пресметка на границите на функцијата.
Цел: стекнување на основни знаења од областа на основните гранки на математиката . Тестирање на асимилација на знаењата за пресметување на границите на функции. Повторете и систематизирајте го знаењето на оваа тема.
Задачи:
Развој на креативно професионално размислување;
Совладување на јазикот на науката, вештини за оперативни концепти;
Совладување на вештините за поставување и решавање проблеми;
Продлабочување на теоретска и практична обука;
Развој на иницијатива и независност на учениците.
Зајакнување на компјутерските вештини;
Продолжете да работите на математичкиот говор.
Формирање вештини за самостојна работа, работа со учебник, вештини за самостојно стекнување знаења;
Развој на способност за истакнување на главната работа при работа со текст;
Формирање на независно размислување, ментални операции: споредба, анализа, синтеза, генерализација, аналогија;
Покажете им на учениците улогата на систематската работа за продлабочување и зголемување на силата на знаењето, на културата на завршување на задачите;
Развој на креативните способности на учениците.
Обезбедување практична работа:
Теоретски материјал на методолошки препораки за практична работа.
Математика, – Серија: Средно стручно образование. - Ростов-на-Дон „Феникс“, стр.
Напредок на практичниот час.
1.Формулирање на темата на часот, објаснување на поврзаноста на темата со други теми од академската дисциплина;
2.Проверка на подготвеноста на учениците за час;
3. Спроведување на вистинскиот час според темата и во согласност со програмата за работа на дисциплината:
Проучете теоретски материјал на тема „Пресметување на границите на функциите“.
Размислете за примери за решавање на типични задачи.
Направете независна работа за пресметување на границите на функциите користејќи ги првата и втората извонредна граница.
Одговори на безбедносните прашања.
Теоретски информации и методолошки препораки
на решавање на проблеми.
1. Презентација на теоретски материјал.
За да ја пресметате границата на функцијата во одредена точка, треба:
1) Заменете наместо променливата x кон што се стреми x.
2) Ако по завршувањето на чекор 1) добиеме несигурност на формуларот https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">и замениме стрелката со минус: (х-а).
3) Доколку, по завршувањето на чекор 1, добиеме несигурност на формуларот https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> поврзани со вредностите на тригонометриските функции, мора да ја искористиме првата извонредна граница.
Дефиниција.Првата извонредна граница се нарекува граница
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Дефиниција:Втората извонредна границанаречена граница

Бројката дадена со оваа граница игра многу важна улога и во математичката анализа и во другите гранки на математиката. Се повикува бројот основа на природни логаритми ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Консолидација на изучениот материјал.
Пример 1
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Го користевме правилото 1) и наместо x го заменивме она кон што треба да се стреми x, т.е. x=2.
Пример 2
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
Пример 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6
Пример 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" height="30 src=">
Пример 5
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
Пример 6
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
б) 
V) 
3. Консолидација на знаења, вештини и способности.
Направете самостојна работа на пресметување на границите на функциите.
Практична работа бр.1. Опција 1 Пресметајте ја границата на функцијата: 1. 2. 3. 10. | Практична работа бр.1. Опција 2 Пресметајте ја границата на функцијата: 1. 2. 3. 10. |
Практична работа бр.2.
Предмет : Наоѓање на извод на функција. Проучување на функција од една променлива и исцртување график.
Цел : Тестирајте во пракса знаење за концептот на извод на функција, способност за наоѓање изводи на елементарни функции, сложени функции, инверзни функции, користејќи табела со изводи и правила за диференцијација, концепт за сложена и инверзна функција, способност да користи извод за проучување на функциите.
Обезбедување практична работа:
Тетратка. „Математика“. - М.: Бустард, 2010 година.
Математика. М: Форум-Инфа 2008 година.
Индивидуални картички со опција за практична работа.
1. Теоретски материјал и примери за наоѓање извод на функција.
Дефиниција:Изводот на функцијата f(x) (f"(x)) во точката x е граница на односот на зголемувањето на функцијата до зголемувањето на аргументот кога зголемувањето на аргументот се стреми кон нула:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
Правила на диференцијација.
Ако функциите f(x) и g(x) имаат изводи, тогаш
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, каде што C=конст
5..png" width="49" height="54 src=">
6. Извод на сложена функција:
f′(g(x))=f′(g) g′(x)
2. Примери.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).
Функцијата е производ на два фактори: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
Функцијата е количник на два израза: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " height="57 src=">.png" width="197 height=36" height="36">
Решение. Ајде да го најдеме изводот на оваа функција користејќи го правилото за диференцијација на сложени функции (формула 6):

5. Ако , тогаш 
6. y = x 3 – 3x 2 + 5x+ 2. Ајде да најдеме y "(–1).
y " = 3x 2 – 6x+ 5. Затоа, y "(–1) = 14.
7. Ако y= дневник x cos x, Тоа y" = (лн x)"кос x+ln x(кос x) " =1/x∙cos x– н xгрев x.
Нека е дадена функција. За да го проучите ви треба:
1) Најдете го неговиот домен на дефиниција. Ако не е премногу тешко, корисно е да се најде и опсегот. (Меѓутоа, во многу случаи, прашањето за наоѓање се одложува додека не се најдат екстремите на функцијата.)
2) Откријте ги општите својства на функцијата што ќе помогнат во одредувањето на нејзиното однесување: дали функцијата е парна или непарна, дали е периодична.
3) Откријте како се однесува функцијата кога аргументот се приближува до граничните точки на доменот на дефиниција, доколку има такви гранични точки. Ако функцијата има точки на дисконтинуитет, тогаш овие точки треба да се проверат и за присуство на вертикални асимптоти на функцијата. Најдете коси асимптоти.
4) Најдете ги пресечните точки на графикот со координатните оски, што се состои од едноставно пресметување на вредноста на функцијата под услов:
Со OX оска: y=0;
Со OY оска: x=0.
Пронаоѓањето на точките на пресек со оската може да доведе до потреба да се реши сложена алгебарска равенка, што, можеби, може да се направи само приближно. Откако ги најдовме корените на функцијата и точките на дисконтинуитет, можеме да го одредиме знакот на функцијата во секој од интервалите помеѓу овие точки. Ова може да се направи или со пресметување на вредноста на функцијата во која било точка од интервалот или со користење на методот интервал.
5) Најдете интервали на монотоност. За да го направите ова, пронајдете го изводот и решете ја нееднаквоста:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, функцијата се намалува.
Откако ги пронајдовме интервалите на монотоност, можеме веднаш да ги одредиме точките на локалниот екстрем: каде што зголемувањето се заменува со намалување, се наоѓаат локални максими, а каде што намалувањето се заменува со зголемување, се наоѓаат локални минимуми.
6) Наоѓањето на интервалите на конвексност и конкавност се врши со помош на вториот дериват..png" width="39" height="19 src="> на интервалите:
ако https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, тогаш кривата на графикот на функцијата е конвексна.
Во исто време, ние ги дефинираме точките на флексија како оние точки во кои функцијата ја менува насоката на конвексност (и е континуирана).
7) Наоѓање на точките на пресек на графикот со асимптота и дополнителни точки. Оваа точка не е задолжителна, но наоѓањето такви точки го прави целосно и целосно проучувањето на функцијата и нејзиниот график.
Забележете дека е корисно веднаш да се исцртаат точките на координатните оски и на графикот што се добиваат при проучувањето на функциите на цртежот. Ова помага да се разбере изгледот на графикот на патот.
3. Направете го тоа сами:
|
опција | Најдете го изводот на функцијата y: |
опција | Најдете го изводот на функцијата y: |
1.y=6- | 1. y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Практична лекција
Предмет:Наоѓање деривати. Примена на изводот за проучување на функции и исцртување графикони.
Цел: Совладајте го пресметувањето на деривати, научете да истражувате функција користејќи го изводот
Средства за образование:тетратки за практични вежби, презентации на тема, Интернет ресурси.
1. Размислете за теоретски материјал на темите: „Правила за пресметување на деривати“, „Екстремум на функција“, „Конвексност, конкавност. Точка на флексија“.
2. Прегледајте примероци од задачи.
3. Заврши тест задача бр.1.
Контролни прашања:
1. Дефинирајте го максимумот (минимумот) на функцијата во точка. Што може да се каже за знакот на зголемување на функцијата во прилично мало соседство на максималната (минимална) точка?
2. Кои се потребните услови за постоење на екстрем на функција? Кое е нивното геометриско значење?
3. Кое е правилото за наоѓање најголеми и најмали вредности на функција на сегмент?
4. Дефинирајте конвексност (конкавност) на крива на интервал.
5. Кое е правилото за наоѓање на интервалите на конвексност и конкавност на крива?
6. Точка на флексија на кривата. Како да ја најдам?
7. Кој е алгоритам за конструирање на график на функција?
Правила за пресметување на деривати
Извод на сложена функција.
Ако на=ƒ( И), u=φ(x), тогаш на¢ ( X)=ƒ¢ (i)·φ¢ (X).
Извод на сума.
Ако на(X)=И(X)+v (X), Тоа на¢ (X)=И¢ (X)+v ¢ (X)
Дериват на производот.
Ако y(x)=u(X)· v (X), Тоа на¢ = И¢ · v + u · v ¢ .
Особено, ( Со· И)¢ =в· И¢, односно константниот фактор се вади од под дериватниот знак. Лесно е да се потврди тоа
(u 2 ) ¢ = 2 у·у ¢ , (у 3 ) ¢ = 3u 2 u ¢ , … , (у n ) ¢ =n·u n–1 u ¢ .
Извод на количник.
Ако тогаш  .
.
Табела со деривати
1. (Со)¢ =0
За сложена функција: ако u=u(x), Тоа:
2. (X)¢ =1
3. (Х α )¢ = α · Xα-1, А– кој било реален број.
 .
.
3. 
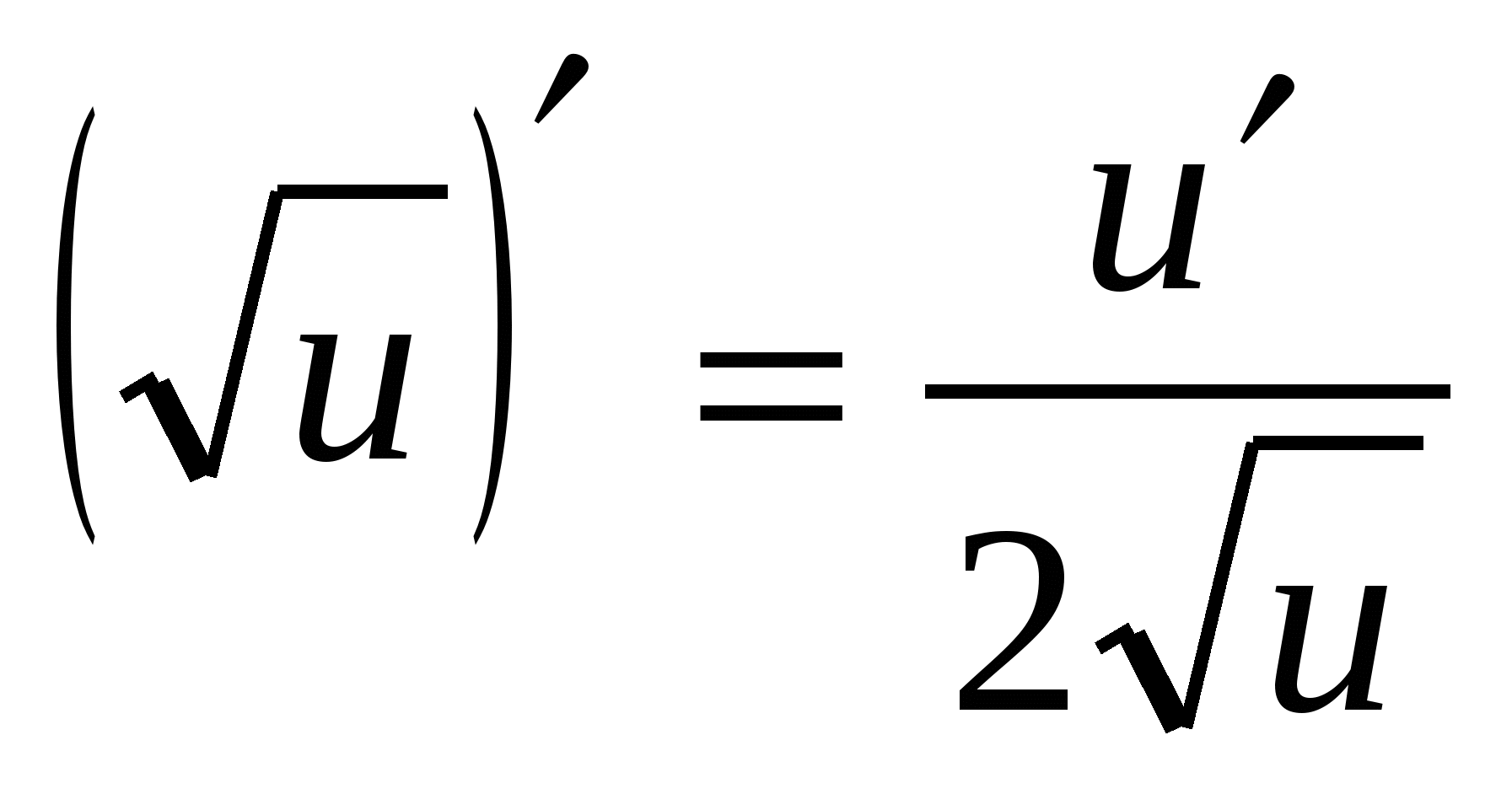
4. (А X ) ¢ =а X · ln А
4. 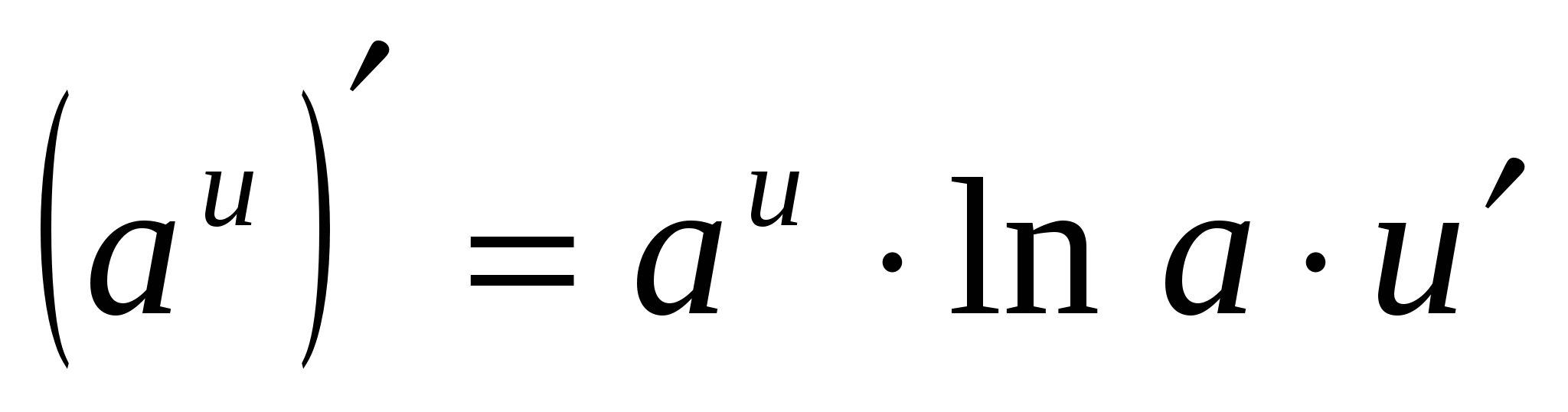
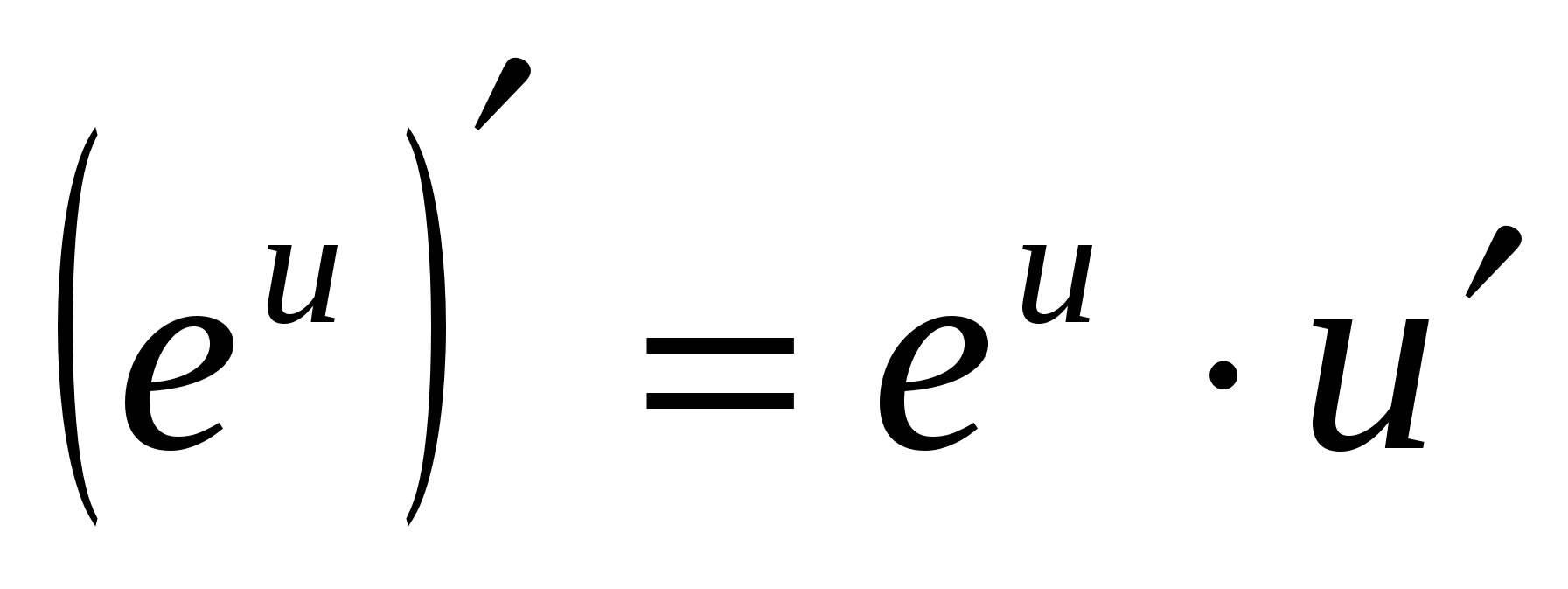
5. (дневник
а
x)
¢
=
 .
.
5. 

6. (грев x)¢ =cos x
6. 
7. (cos x)¢ = –грев х
7. 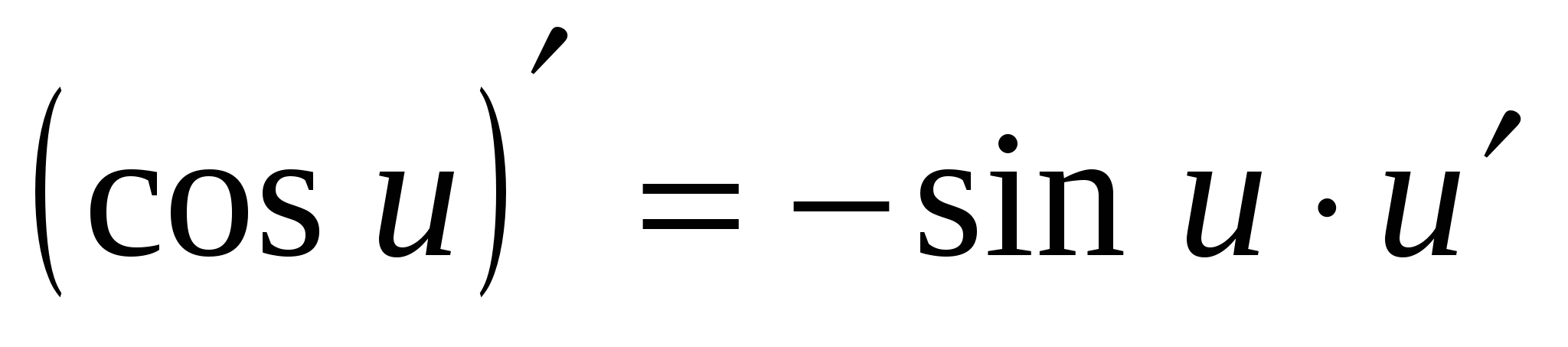
8. (tg x)¢
=
8. 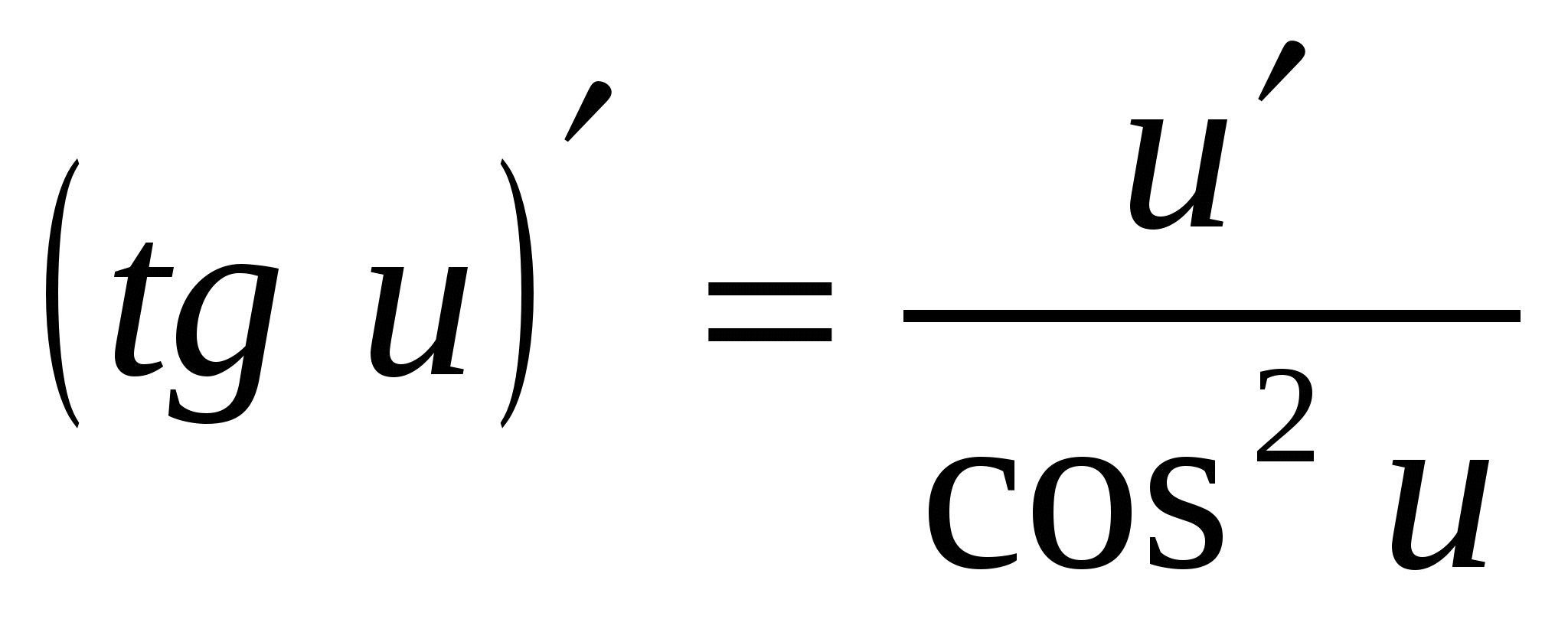
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 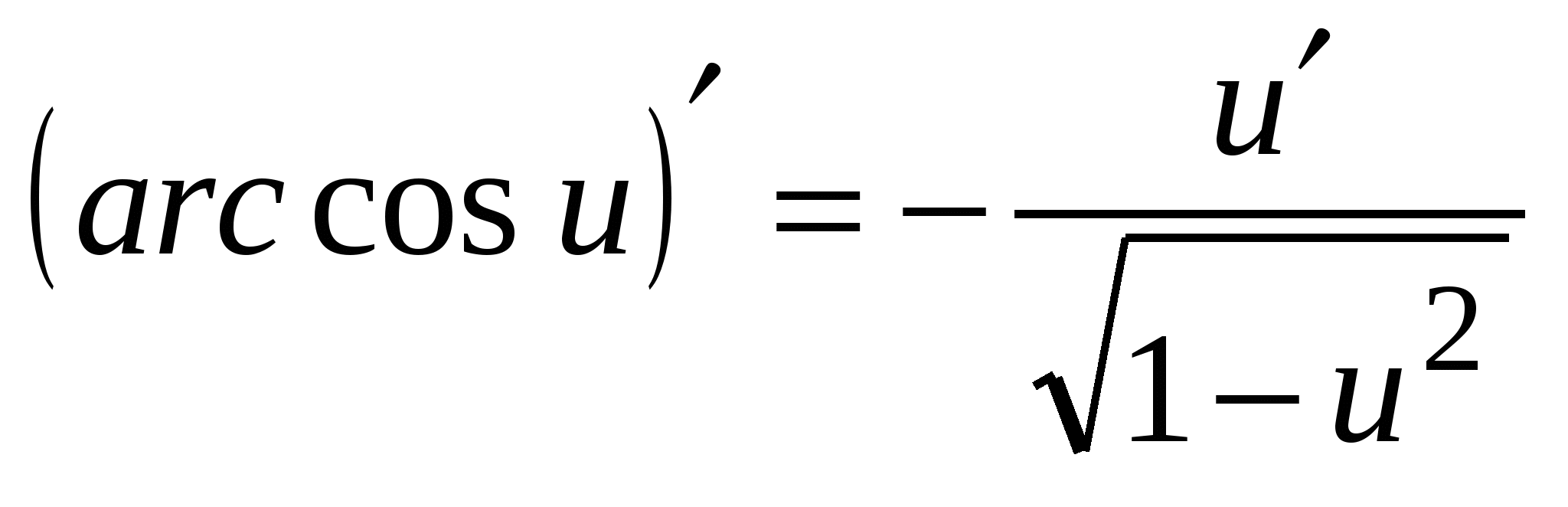
12. 
12. 
13. 
13. 
Преглед на примери
Пример 1.
y=(3–2 грев 5x ) 4 | Ние применуваме деривативни формули за И α ,грев u |
y ¢ =4·(3-2·sin5x) 3·(3-2sin5x) ¢ =4·(3–2·грев5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
Пример 2.
. 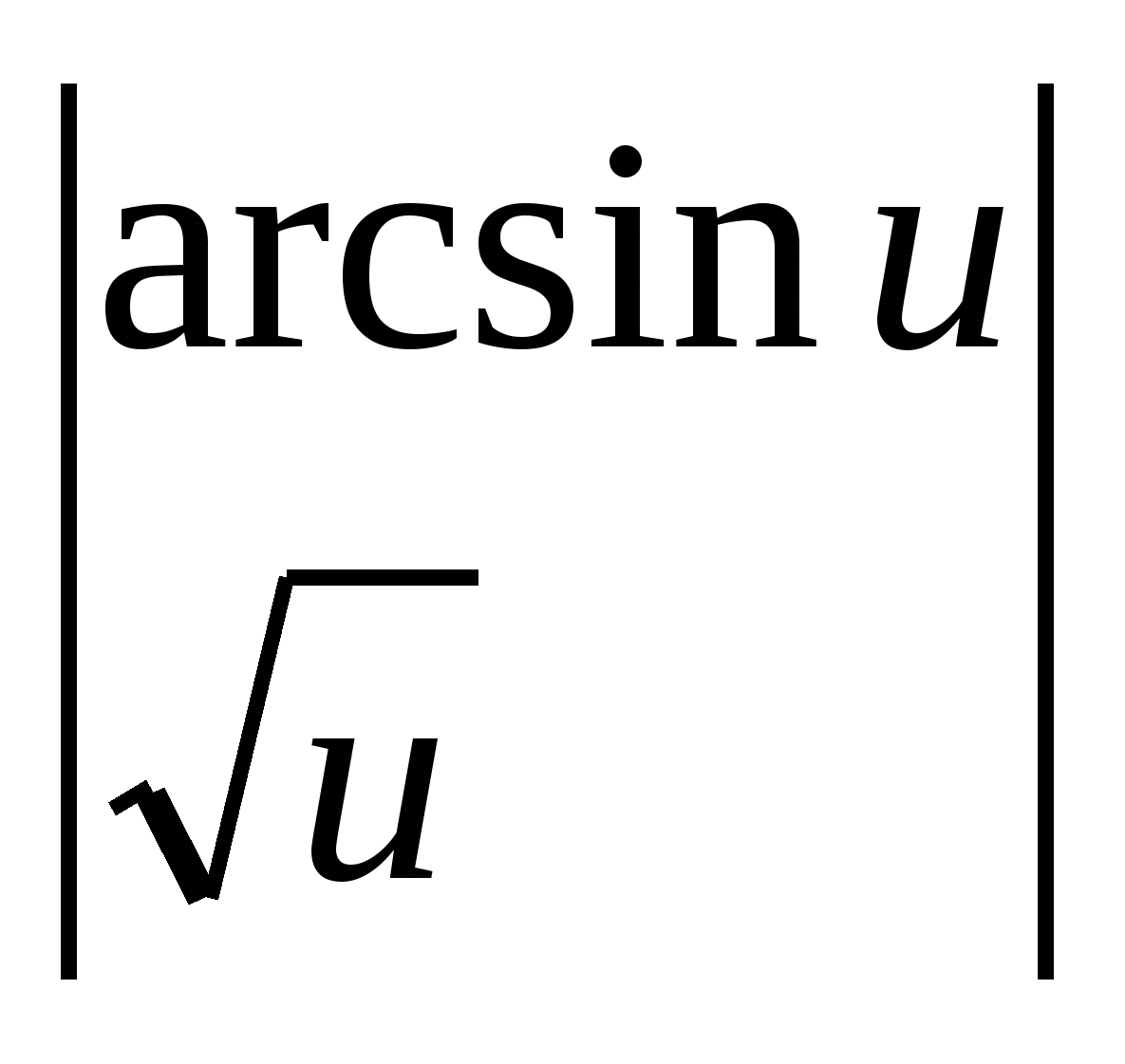

Пример 3.
 .
. 

Пример 4.



Пример 5.
 .
. 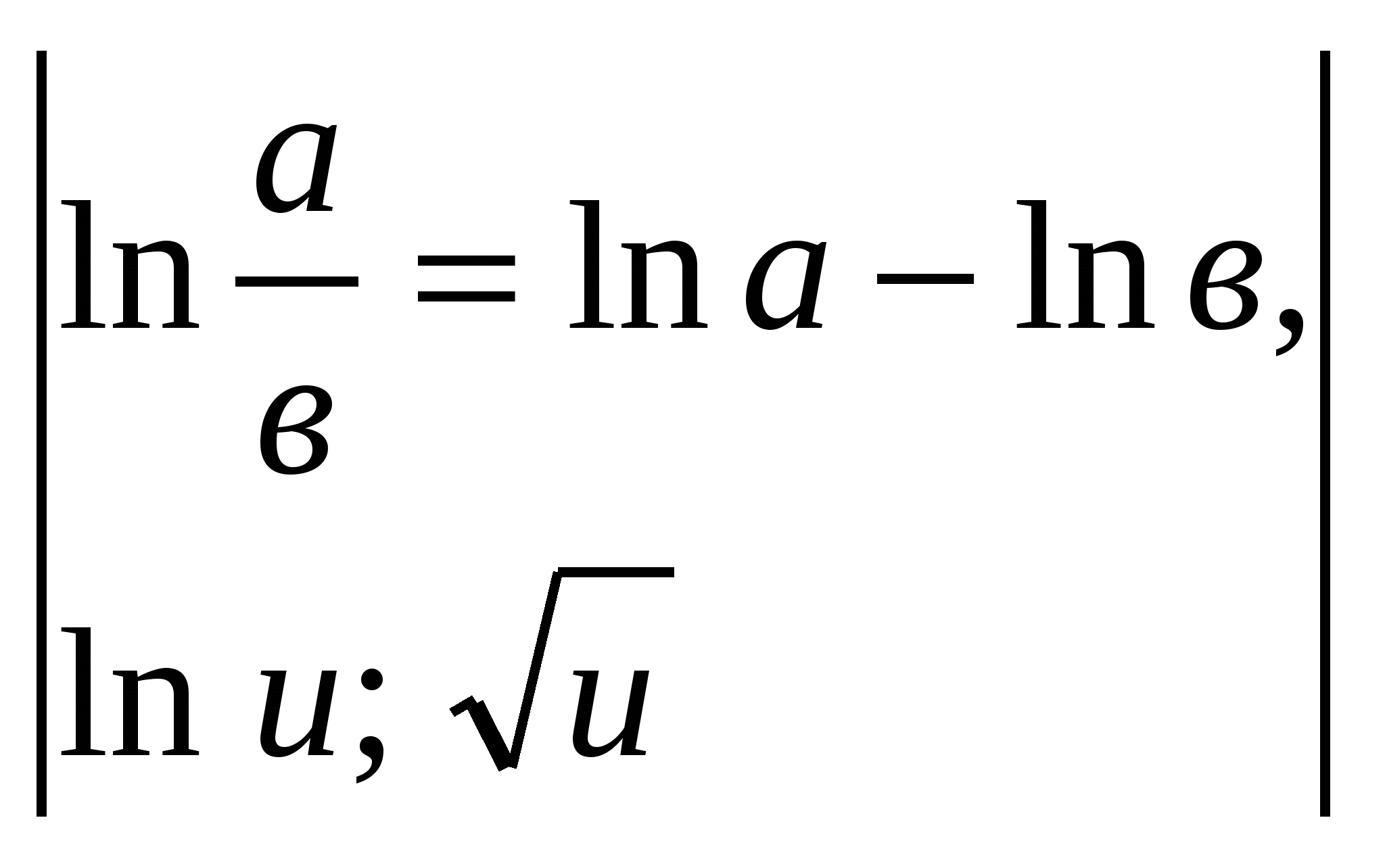

Екстрем на функцијата
Проучувањето на функцијата на екстремите е една од најважните примени на дериватите. Ајде да ја разгледаме дефиницијата за минимум и максимум и како да ги најдеме.
Нека функцијата ƒ( X) е дефинирана и диференцијабилна на одредено множество и точка X 0 е точка во него.
Дефиниција.Функција ƒ (X) во точка X 0 има максимум(минимум), доколку постои такво соседство на точката X 0, што е за секого Xод оваа област ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Точка X 0 тогаш се нарекува точка максимум(минимум).

Ориз. 1.
Прикажан е график на функција која има две максимални точки ( X 1 и X 3) и два минимум поени ( X 2 и X 4), а максималната вредност може да биде помала од минималната ( ƒ (X 1 ) < ƒ (X 4)). Ова го нагласува фактот дека ние ја карактеризираме сингуларноста на функцијата само во близина на одредена точка.
Вредностите на функцијата во точките на максимум и минимум се нарекуваат екстремни вредности или крајности. Горниот графикон покажува дека екстремните точки ( X 1 , X 2 , X 3 , X 4) определи ги интервалите на монотоност на функцијата, во секоја од нив дериватот задржува одреден знак. Во екстремните точки, се разбира, дериватот оди на нула. Да формулираме теорема за неопходен услов постоење на екстрем.
Теорема.Доколку функцијата ƒ (X) во точка X 0 има екстрем, тогаш изводот на функцијата во оваа точка е еднаков на нула, т.е. ƒ¢ ( X 0)=0.
Веднаш да забележиме дека овој услов не е доволен, односно обратното тврдење не е секогаш точно. Од еднаквост ƒ ¢ ( X 0)= 0 не мора да значи дека во точката X 0 постои екстрем.
Ова е потврдено со пример со функцијата ƒ (X)=x 3 .
Ќе најдеме ƒ ¢ ( X)= 3X 2 . Во точката X=0 ƒ ¢ (0)=0 . Но колку сакаш блиску до поентата X=0 ќе најдеме X> 0, каде ƒ (X)=x 3 > 0, ќе најдеме X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, каде за сите Xвредност на функцијата во точка X=0 ќе биде најголемиот или најмалиот. Затоа точка X=0 не е екстремна точка.
Човек може да се расправа поинаку. Бидејќи дериватот ƒ ¢ (x)=3x 2 , потоа функцијата ƒ(x)=x 3 се зголемува за секој реален x и нема екстреми.
Точки во кои е задоволена потребната екстремна состојба (ƒ ¢ (x)=0)се нарекуваат критички .
Очигледно, тангентата на графикот на функцијата во точките каде што ƒ ¢ (x)=0,паралелно со x-оската Ox .
Доволна состојбаекстрем е даден во следните теореми.
Теорема 1.Ако X 0 е критичната точка на функцијата и при минување низ неа изводот го менува знакот, тогаш X 0 е екстремна точка, имено, ако изводот го промени знакот од плус во минус, тоа е максимална точка, а ако го промени знакот од минус во плус, тоа е минимална точка.
Забележете дека нема екстрем во точка ако изводот не го промени знакот. Од училишниот курс е познато правилото за изучување на екстремите со користење на првиот дериват. Понекогаш е попогодно да се формулира доволен услов за екстрем со користење на вториот дериват.
Нека функцијата ƒ( X) е двапати диференцијабилна во некој домен (т.е. ƒ( X) има ƒ¢ ( X) И ƒ ¢¢ ( X)).
Теорема 2.Ако X 0 – критична точка на функцијата ƒ(x)и ƒ ¢¢ (Х 0 ) > 0 , Тоа X 0 – минимален поен, ако ƒ ¢¢ (Х 0 ) < 0, то X 0 – максимална поен.
Со помош на вториот извод се одредува конвексноста или конкавноста на графикот на функцијата.
Конвексност, конкавност. Точка на флексија.
Кривина y=ƒ(X) се нарекува конвексноти подолубило која од неа тангента
ƒ ¢¢ ( X) < 0.
Кривина y=ƒ(X) се нарекува конкавна на интервал ако лежат сите точки на кривата повисоко било која од неа тангента на овој интервал. Потоа на овој интервал
ƒ ¢¢(x) > 0
Дефиниција. Точка на флексија Крива е точка каде што од едната страна кривата е конвексна, а од другата е конкавна.
На точката на флексија ƒ ¢¢ ( X)=0.
Значи, знакот на вториот извод (како и знакот на самата функција и нејзиниот прв извод) ги означува карактеристиките на графикот на функцијата. Ајде да ги погледнеме повторно.
Ако за сите Xна интервалот ( А, б) ƒ (X) > 0 (ƒ (X) < 0), тогаш графикот лежи над (под) оската x.
Ако за сите Xна интервалот ( А, б) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (А, б) се зголемува (намалува).
Ако за сите Xна интервалот ( А, б) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (А, б) конкавен (конвексен).
Равенка ƒ( X)=0 ги дефинира „нулите“ на функцијата, односно точките на пресек на графикот со оската Ox.
Равенката ƒ ¢ ( X)=0 ги дефинира критичните точки.
Равенката ƒ ¢¢ ( X)=0 ги дефинира можните точки на флексија.
Шема за проучување на функции
Да ја проучува функцијата ƒ (X) и заговор y=ƒ(X) треба да се најде:
1) доменот на дефинирање на функцијата и пресечната точка на графикот со координатните оски;
2) интервали на монотонија;
3) точки на екстремни и функционални вредности во овие точки;
4) интервали на конвексност и конкавност на графикот;
5) точки на флексија на графикот;
6) конструирајте во Декартов координатен систем сите добиени точки (понекогаш, за да се разјасни графикот, се добиваат дополнителни точки) и самиот график.
Најмалите и најголемите вредности на функцијата на сегмент
При решавање на некои проблеми на методот на оптимизација, важно е да може да се најдат најмалите или најголемите вредности на функцијата на одреден сегмент. Функцијата ги достигнува овие вредности или во критичните точки или на краевите на сегментот.
Шема за пребарувањенајмалите и најголемите вредности на функцијата ƒ (X) на сегментот [ А, б].
1. Најдете го изводот на функцијата ƒ ¢ ( X).
2. Најдете ги критичните точки од равенката ƒ ¢ ( X)=0.
3. Изберете ги оние критични точки кои припаѓаат на овој сегмент [ А, б] и пронајдете ја вредноста на функцијата ƒ (X) во секоја таква точка.
4. Пресметајте ги вредностите на функциите ƒ (X) на краевите на отсечката: ƒ( А) и ƒ( б).
5. Од добиените функциски вредности изберете најголема (најголема) и најмала (најмала).
Пример 2.
Најдете ги најголемите и најмалите вредности на функцијата ƒ(x)=X 3 – 9x 2 +24х–10на сегментот.
1. ƒ ¢ ( X)= 3X 2 – 9·2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. Точката x 2 =4 не припаѓа на отсечката. Затоа, ја пресметуваме вредноста на функцијата само во точката X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Вредности на функциите на краевите на сегментот: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Добиени вредности:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Највисоката вредност е 10 и се постигнува во точката X=2. Најмалата е еднаква на –10 и се постигнува во точката X=0.
Пример 3.
Најдете ги интервалите на конвексност и конкавност и точки на флексија на кривата y=x+36X 2 –2X 3 –X 4 .
Доменот на дефиниција на оваа функција е множеството од сите реални броеви, т.е. XЄ(–∞, +∞).
Ајде да го најдеме вториот извод.
на¢ =1+72 X–6X 2 –4X 3 .
на¢¢ =72–12 X–12X 2 = –12(X 2 +X–6).
Од равенството. на¢¢ =0 ја добиваме апсцисата на точката на флексија:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
Ајде да го дефинираме знакот на¢¢ во интервали
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
на¢¢
крива форма
конвексни
флексија
конкавна
флексија
конвексни
Да ги најдеме ординатите на точките на флексија:
на(–3)=726; М 1 (–3; 726) – точка на флексија
на(2)=114; М 2 (2; 114) – точка на флексија.
На интервалот (–3; 2) кривата е конкавна. На интервалите (–∞; –3) и (2; +∞) – конвексни.
Примероци од задачи
Задача бр. 1.
Најдете ги точките на прекин на функцијата и нацртајте го графикот

Функција ƒ (X) се дефинира за сите реални Xи е континуиран на секој од наведените интервали: (–∞; –1), [–1; 0], (0, +∞). Ајде да ја истражиме функцијата ƒ (X) за континуитет во точките X= –1 и X=0.
За да го направите ова, ќе најдеме еднострани граници на секоја од овие точки.

Бидејќи едностраните граници се различни, тогаш X = –1 – точка на дисконтинуитет од првиот вид.
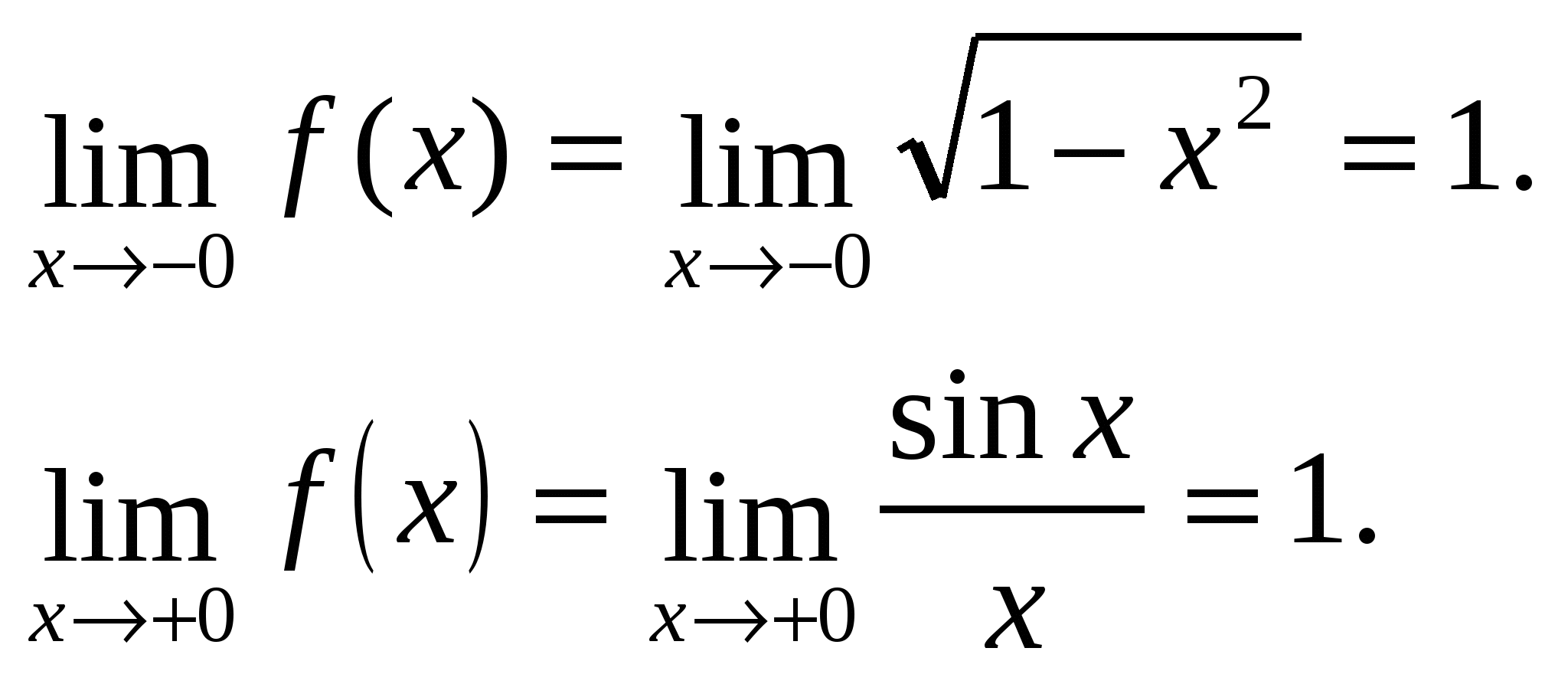
Едностраните граници се еднакви, односно во точката x=0 постои граница на функцијата и 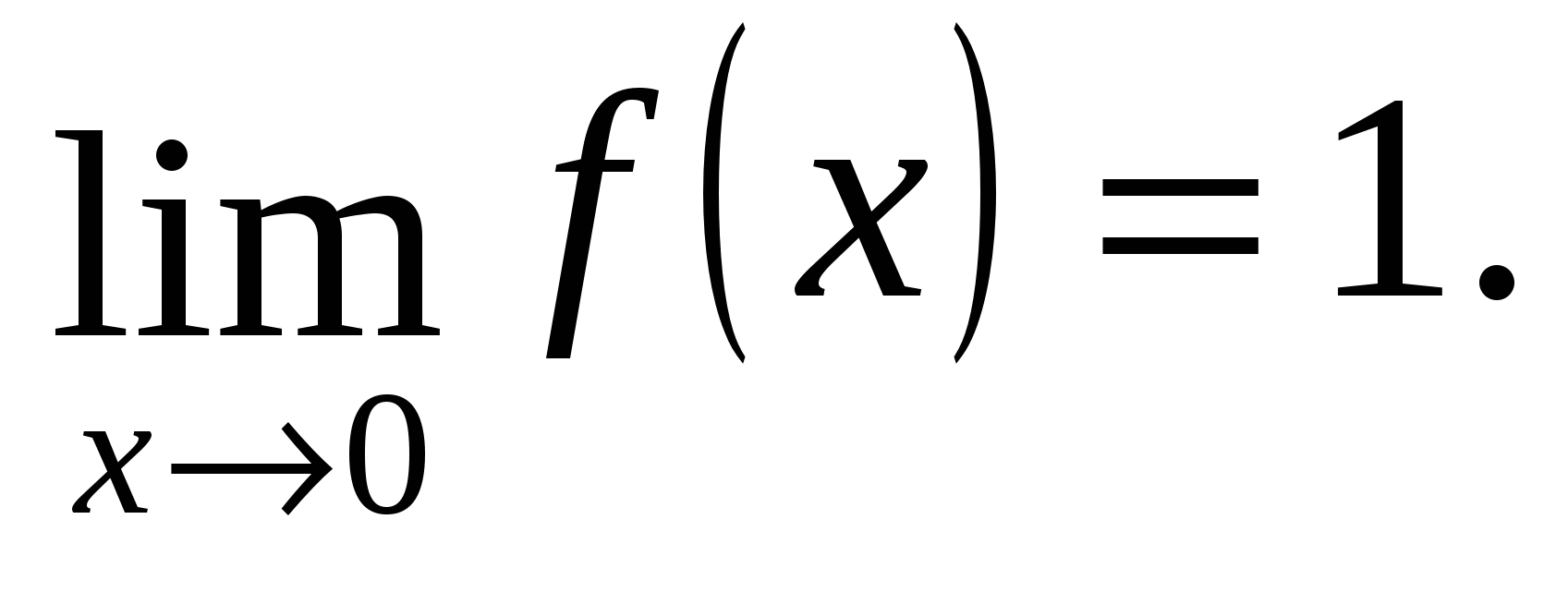
Ајде да ја споредиме оваа граница со вредноста на функцијата во точката: 
Бидејќи  потоа во при x=0 функцијата ƒ(x) е континуирана.
потоа во при x=0 функцијата ƒ(x) е континуирана.
Да ја нацртаме функцијата ƒ (X), со оглед на тоа
1)  - равенка на права линија,
- равенка на права линија,
2)  – равенка на горниот полукруг
– равенка на горниот полукруг  со центар на почетокот и радиус еднаков на единство, а под услов –1 £ X£ 0 равенка
со центар на почетокот и радиус еднаков на единство, а под услов –1 £ X£ 0 равенка  дефинира четвртина круг.
дефинира четвртина круг.
3) за X > 0 графикот е даден со равенката  . Пресечните точки на оваа крива со оската Ox ги наоѓаме од равенката
. Пресечните точки на оваа крива со оската Ox ги наоѓаме од равенката 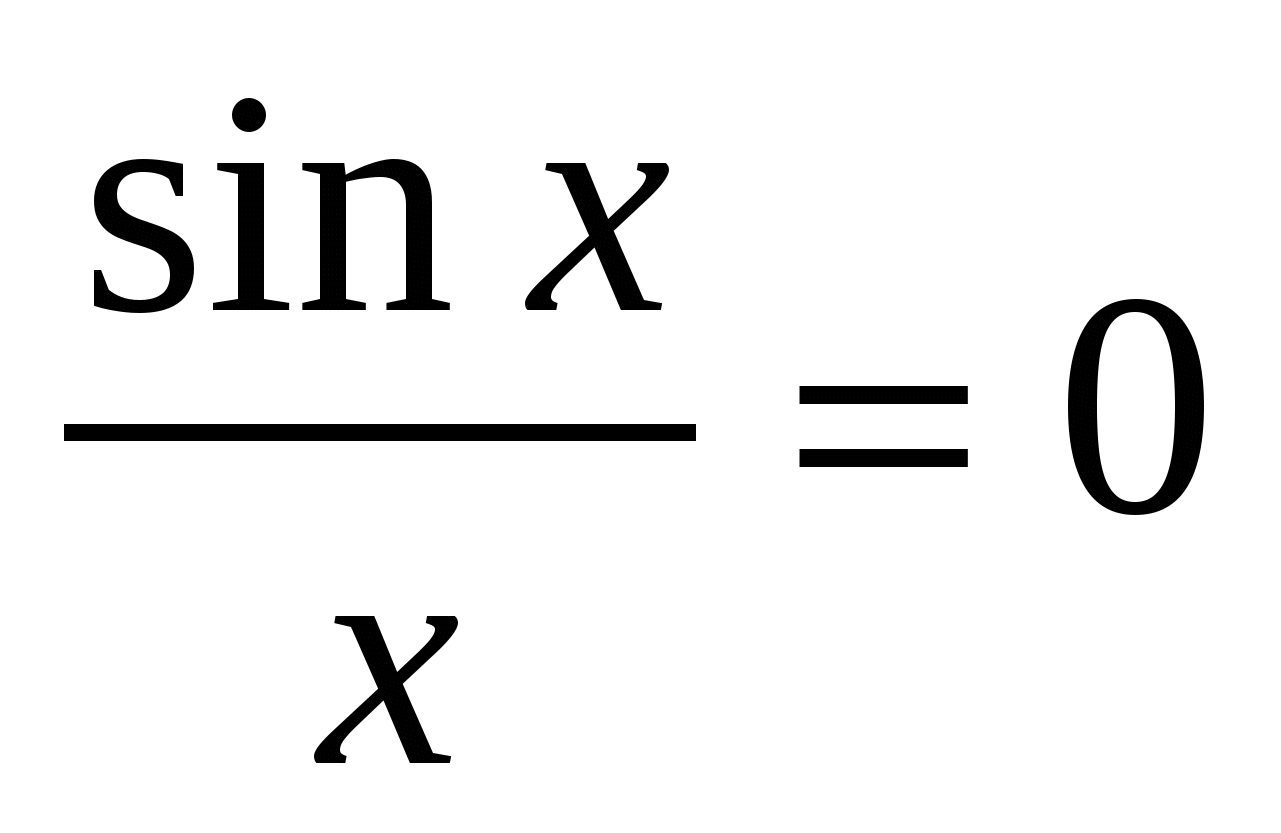 за x > 0. x= π
n, Каде n
=1, 2, 3, 4,
за x > 0. x= π
n, Каде n
=1, 2, 3, 4,

Ориз. 2.
Задача бр. 2.
Напиши равенки за тангенти на права  на точките каде што X=0 и X=4. Најдете ја точката на пресек на тангентите и аголот меѓу нив. Направете цртеж.
на точките каде што X=0 и X=4. Најдете ја точката на пресек на тангентите и аголот меѓу нив. Направете цртеж.
Равенка на тангента на права y=ƒ(x)изгледа како
Каде на 0 =ƒ( X 0).
Во точката X=0 на(0)=ƒ(0)=5.
на¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
М 1 (0, 5) ја има формата y- 5= –3(X–0) или
y= –3X+5.
Во точката X=4 на(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Равенка на тангента во точка М 2 (4, 1) ја има формата y- 1=X-4 или
y=x–3.
Пресечната точка на тангентите ја добиваме со решавање на системот

Пресечна точка М 3 (2, –1).
Катче φ помеѓу тангентите наоѓаме од формулата:
 ,
,
Каде к 1 = –3; к 2 =1 – аголни коефициенти на тангенти.
 .
.
Катче φ =arctg 2.
Ајде да ја изградиме оваа линија  – парабола со теме во точката каде X= 3, бидејќи на¢
=0 во X=3. Ќе најдеме
– парабола со теме во точката каде X= 3, бидејќи на¢
=0 во X=3. Ќе најдеме  . Точка М 4 (3;
. Точка М 4 (3;  ) е темето на параболата.
) е темето на параболата.
Р 
е. 3.
Задача бр.3.
Функција за истражување 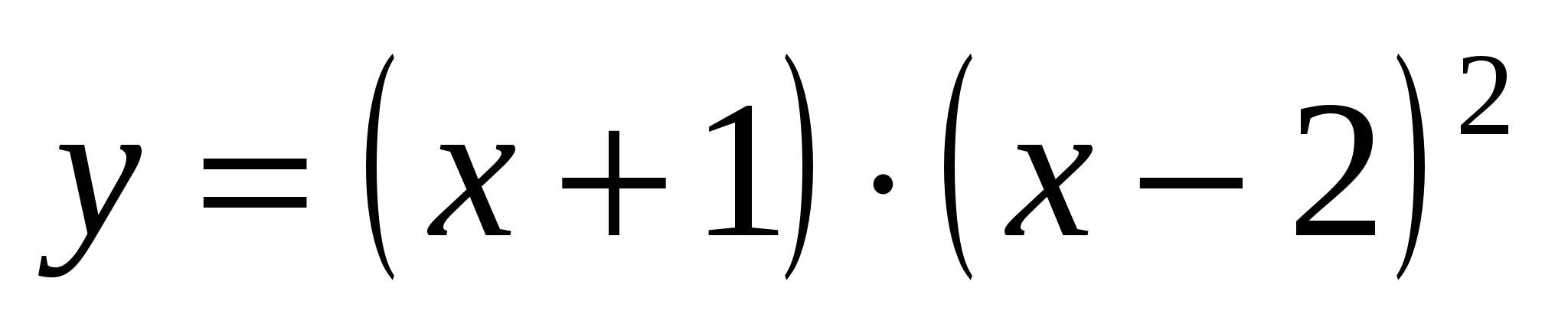 и заговор.
и заговор.
1. Оваа функција е полином (можете да ги отворите заградите, добиваме полином од трет степен), затоа е дефинирана, континуирана и диференцијабилна за било кој X.
2. Да го најдеме изводот.
 .
.
Од равенството. на¢ =0 ајде да најдеме критични точки: 3 X·( X–2)=0, X 1 =0, X 2 =2.
Ајде да ги истражиме.
X
(–∞, 0)
(0; 2)
(2; +∞)
на ¢
на
3. Значи, функцијата се зголемува на интервалите (–∞, 0) и (2, +∞), се намалува на интервалот (0; 2), има максимум на x=0 и минимум на x=2:
на макс = на(0)=4; намин = на(2)=0.
4. Да го најдеме вториот извод.
на¢¢ = 6·( X-1).
Кривата е конвексна каде на¢¢ < 0, т. е. 6·(X–1) < 0, X < 1.
Кривата е конкавна каде на¢¢ > 0, т.е. X > 1.
Значи, на интервалот (–∞, 1) кривата е конвексна; а на интервалот (1, +∞) е конкавен.
5. Од равенката ја наоѓаме точката на флексија на¢¢ =0. Така, X=1 – апсциса на точката на флексија, бидејќи оваа точка ги одделува интервалите на конвексност и конкавност на кривата. Ординати на точка на флексија: на(1)=2.
График на функција на=(X+1)·( X–2) 2 ја сече оската Ox на на=0, т.е. кога X= –1 и X=2;
ја преминува оската Ој кај X=0, т.е. кога на=4. Добивме три бода: (–1; 0), (2; 0), (0; 4). Сите добиени поени ќе ги внесеме во табелата, додавајќи ги оние што се соседни до нив.
–2
–1



–16


е. 4 Крива y=(x+1)(x–2) 2.
Задача бр. 1
Ви претставуваме задачи кои може да имаат еден, два, три или повеќе точни одговори. Заокружи ги броевите на сите точни одговори.
1. Ако  потоа функцијата
потоа функцијата
1) зголемување
2) се намалува
3) константна
2. Ако
1) Зголемување
2) Намалување
3. Ако  , потоа функцијата
, потоа функцијата
1) Зголемување
2) Намалување
4. Ако  , потоа функцијата
, потоа функцијата
1) Зголемување 3) Намалување
2) Постојана 4) Монотона
5. Функција  Е
Е
1) Дури
2) Ниту
3) ниту парни ниту непарни
4) Периодични
5) Не периодично
6) Тригонометриски
7) Основно
6. Функција  Е
Е
1) дури
2) непарен
3) ниту парни ниту непарни
4) периодични
5) не периодично
6) тригонометриски
7) основно
2) Вајерштрас 4) Дирихле 6) Лајбниц
8) Решение  Равенки
Равенки
1) 0 3) 0 и 3 5) 2 7) 3
2) 2 и 3 4) 2 6) -5 и 1 8) 5 и 1
9) решение на нееднаквоста 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 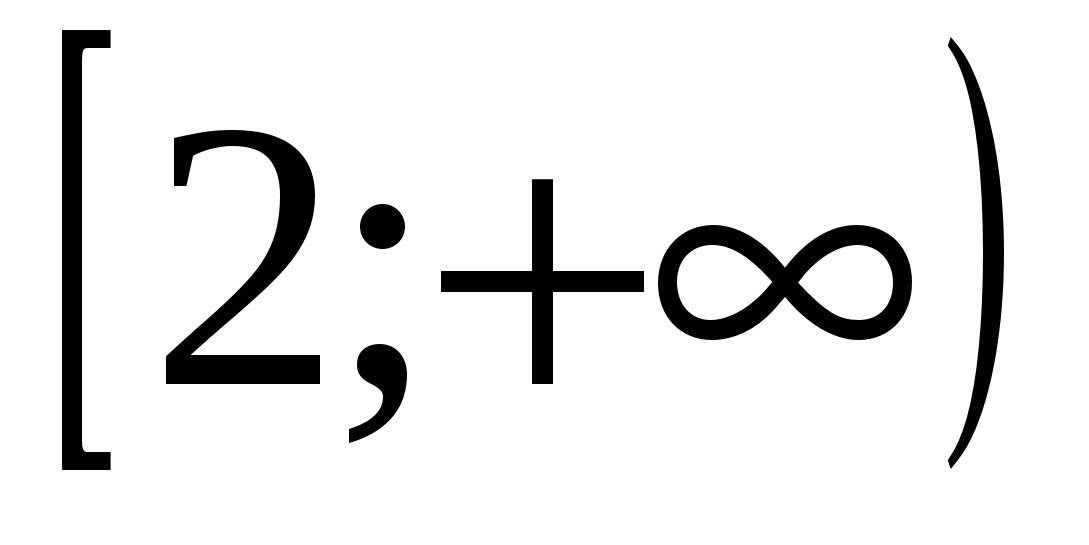
10) Метод  Износот е пронајден
Износот е пронајден
1) вектори
2) директно
3) сегмент
11) Ако  , потоа функцијата
, потоа функцијата
1) Конкавна 3) Конвексна 5) Намалувачка
2) Монотони 4) Зголемувачки 6) Константни
12) доменот на дефинирање на функцијата е еднаков на 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 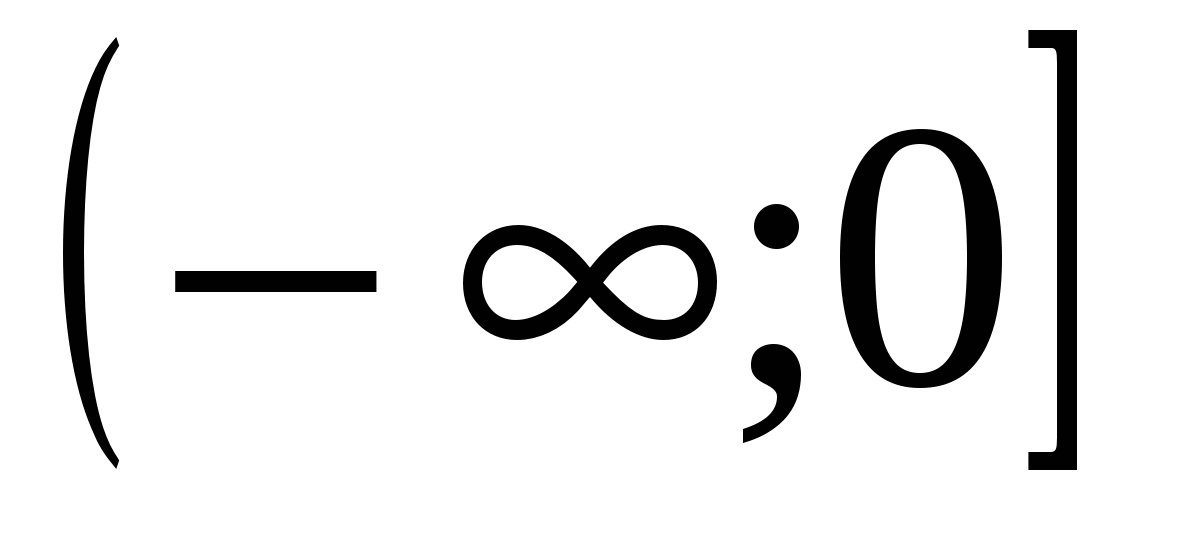
7) (-1;1)
8) 
9) 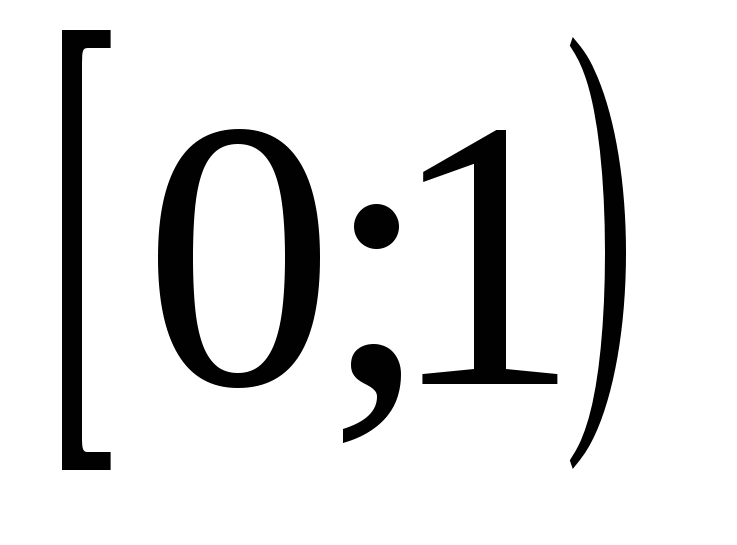
13) функција  е
е
1) индикативно
2) тригонометриски
3) моќ
4) логаритамски
14) ако функциите y = x  тогаш таа е
тогаш таа е 
1) дури
2) непарен
3) ниту парни ниту непарни
15) функција  на
на  е
е

 .
.


