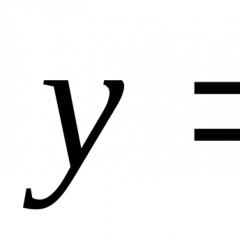Тестови за конвергенција на неправилни интеграли. Како да пресметате несоодветен интеграл и да ја дознаете неговата конвергенција. Дефиниција и основни својства

Теорема 12.11 (тест за споредба на неправилни интеграли). Нека функциите f(x) и g(x) се континуирани на интервалот [a, ">) и го задоволуваат условот 0 фикс) ?(x) на него. Потоа од конвергенција на интегралот

интегралот конвергира

и обратно, од дивергенцијата на интегралот (12.64) следува дивергенција на интегралот (12.63).

Доказ.Да ја воведеме следната нотација:

Функција P(K)не се намалува; всушност, ако и јас 2, тогаш

Ј поправете) dx>0, а потоа

Ајде да земеме низа вредности (/?„) -> „>; потоа соодветната низа од вредностите на функциите (F(Rn))е монотон и не се намалува. Нека интегралот (12.63) се спојува, па низата (67 ( Ртоа)) е ограничено; но тогаш и низата е ограничена (Ф(/?„)), што значи дека со теорема 7.13 се конвергира. Затоа постои граница F(R)на Р-+ «>, т.е. интегралот (12,64) конвергира.

Сега да го докажеме вториот дел од теоремата; нека се разминува интегралот (12,64). Ако претпоставиме дека интегралот (12.63) конвергира, тогаш, според она што беше погоре докажано, треба да се конвергира и интегралот (12.64), што е во спротивност со условот. Теоремата е докажана. ?

Коментар.Сличен споредбен критериум важи и за неправилни интеграли од вториот вид. Ако функциите /(x) и е (X)континуирано на полуинтервал [а>б)а за сите точки во некое соседство на еднината точка бзавршено

услови 0 (x), тогаш од конвергенцијата на интегралот Jg(x)dx произлегува дека

дивергенцијата на интегралот J/(x)dx, и од дивергенцијата на интегралот J/(x)dx -

моќност на интегралот Jg(x)dx.

Да разгледаме примери за проучување на конвергенција на несоодветни интеграли.

Пример 27. Т. ^-.

X 3 (1 + e L)

Решение.Да го споредиме интеградот во овој интеграл со функцијата

Дг. Очигледно е дека -r-

X g* (1+0 x J

gral J-jdx конвергира; затоа, врз основа на споредбениот критериум, дадената 1 X

национален интеграл.

Пример 28. I-.

Решение.Споредувајќи го интеградот на овој интеграл со функцијата 1/x,

гледаме дека (1 + во x)/x > 1/x на интервалот 1

диверзифицира, затоа, за споредба, овој интеграл, исто така, се разминува.

Како заклучок, без доказ го прикажуваме критериумот на Коши за конвергенција на неправилен интеграл од првиот вид.

12.10.4. Апсолутна и условна конвергенција на неправилни интеграли

Дефиниција 5. Неправилен интеграл J/(x)dx се нарекува апсолутно

конвергентен, ако интегралот J|/(x)|dx конвергира.

Дефиниција 6. Неправилниот интеграл J /(x) dx се нарекува условно слични

траен, ако се конвергира и интегралот J|/(x)|dx дивергира.

Забележете дека апсолутната конвергенција на интегралот подразбира нејзина конвергенција поради проценката 3 определен интеграли критериумот Коши.

Теорема 12.13 (Дирихле-Абел тест*). Нека функцијата /(x) е континуирана и има ограничен антидериват Ф(x) на интервалот [a, «>], а функцијата g(x) има континуиран извод на овој интервал, не се зголемува и се стреми кон нула како x -> ©o. Потоа неправилниот интеграл

конвергира.

Доказ.Дозволете ни да примениме интеграција по делови на интегралот J /(x)g(x)dx

на произволен сегмент R R"Со [ А, °°). Ние имаме:

Теорема 12.12. За неправилниот интеграл (12.64) да се конвергира, потребно е и доволно за било кој e > 0 да се најде таков број А> 0, што за било кој Р"и /?“, поголема од А,нееднаквоста важи:

Според условите на теоремата F(x)ограничен, т.е. |F(x)| K. Функцијата g(x) не се зголемува и се стреми кон нула како x -” “>, што значи. g(x)> 0, a g"(x)

Абел Нилс Хенрик (1802-1829) - норвешки математичар.

Бидејќи, според условите на теоремата, g(x) -» 0 за x -> ©°, за произволен број e > 0 можеме да го најдеме бројот А>така што кога Р" > Лќе се задоволи нееднаквоста g(R") Заменувајќи го ова во проценка (12.68), добиваме:

што одговара на Кошиовиот критериум за конвергенција на интегралот (12.66). Теоремата е докажана. ?

Да разгледаме примери за користење на Дирихле-Абел тест за конвергенција на несоодветни интеграли.

Пример 29. f^^dx, a>0.

Решение.Да ставиме /(x) = sin x, g(x)= l/x"; лесно е да се потврди дека сите услови на теоремата се задоволени, односно овој интеграл конвергира. За > 1, овој интеграл

рал апсолутно конвергира. Навистина, |грев x/xP 1/d L, интеграл J(l/x e)dx

конвергира, т.е. Со споредбениот критериум (теорема 12.11), овој интеграл исто така апсолутно конвергира.

Пример 30. Jsin x 2 dx - Френелов интеграл, о

Решение.Да го претставиме овој интеграл како збир:

Од гревот x 2 - континуирана функцијана интервалот (0, 1J, првиот интеграл во (12.69) постои. За да ја одредиме конвергенцијата на неправилниот интеграл од десната страна на (12.69), поставивме /(x) = x sin x 2, е(x) = 1/x. Потоа за функцијата /(x) антидериватот F(x) = -cosx 2 /!е ограничен на интервалот |1, ">), а #(x) е позитивен, се стреми кон нула како x -" °° и има континуиран извод на (1, ©о). Тоа значи дека според критериумот Дирихле-Абел, вториот интеграл во (12.69) конвергира, т.е. Френеловиот интеграл исто така конвергира.

Како што знаете, наоѓањето на интегралот може да биде прилично тешка задача. Би било големо разочарување да почнете да пресметувате неправилен интеграл и на крајот од патеката да откриете дека тој се разминува. Затоа, од интерес се методите кои овозможуваат, без сериозни пресметки врз основа на еден тип на функција, да се донесе заклучок за конвергенција или дивергенција на несоодветен интеграл. Првата и втората теорема за споредба, кои ќе бидат разгледани подолу, во голема мера помагаат да се проучат несоодветните интеграли за конвергенција.

Нека f(x)?0. Потоа функциите

монотоно се зголемуваат во променливите t или -g (бидејќи земаме g>0, -g се стреми кон нула од лево). Ако, како што се зголемуваат аргументите, функциите F 1 (t) и F 2 (-d) остануваат ограничени одозгора, тоа значи дека соодветните неправилни интеграли се спојуваат. Ова е основата на првата компаративна теорема за интеграли на ненегативни функции.

Нека функциите f(x) и g(x) на x?a ги задоволуваат следните услови:

• 1) 0?f(x)?g(x);
• 2) Функциите f(x) и g(x) се непрекинати.

Потоа од конвергенцијата на интегралот следи конвергенција на интегралот, а од дивергенцијата на интегралот следи дивергенцијата

Бидејќи 0?f(x)?g(x) и функциите се континуирани, тогаш

По услов, интегралот конвергира, т.е. има конечна вредност. Затоа, интегралот исто така конвергира.

Сега нека интегралот се разминува. Да претпоставиме дека интегралот конвергира, но тогаш интегралот мора да конвергира, што е во спротивност со условот. Нашата претпоставка е неточна, интегралот се разминува.

Споредбена теорема за неправилни интеграли од втор вид.

Нека за функциите f(x) и g(x) на интервалот , се зголемуваат без ограничување за x>+0. За x>+0, важи следнава неравенка:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.

Споредбена теорема за неправилни интеграли од 1-виот вид.

Нека функцијата f(x) и g(x) е на интервалот , а сегментот за интеграција е конечен, односно ограничен со броеви, а не со бесконечност. Некои задачи доведуваат до потреба да се напуштат овие ограничувања. Така се појавуваат неправилни интеграли.

Геометриско значење на неправилниот интегралИзлегува сосема едноставно. Во случај кога графикот на функција y = ѓ(x) е над оската Вол, дефинитивниот интеграл ја изразува областа на криволинеарен трапез ограничен со крива y = ѓ(x) , х-оска и ординати x = а , x = б. За возврат, неправилниот интеграл ја изразува областа на неограничен (бесконечен) криволинеарен трапез затворен помеѓу линиите y = ѓ(x) (на сликата подолу - црвено), x = аи оската на апсцисата.

Несоодветните интеграли се дефинирани слично за други бесконечни интервали:

Областа на бесконечно заоблен трапез може да биде конечен број, во тој случај неправилниот интеграл се нарекува конвергентен. Областа може да биде и бесконечност, а во овој случај неправилниот интеграл се нарекува дивергентен.

Користење на границата на интеграл наместо самиот неправилен интеграл.За да го оцените неправилниот интеграл, треба да ја користите границата на определениот интеграл. Ако оваа граница постои и е конечна (не е еднаква на бесконечноста), тогаш неправилниот интеграл се нарекува конвергентен, а во спротивно - дивергентен. Кон што тежнее променливата под знакот за граница зависи од тоа дали имаме работа со несоодветен интеграл од првиот или од вториот вид. Ајде да дознаеме за ова сега.

Неправилни интеграли од прв вид - со бесконечни граници и нивна конвергенција

Неправилни интеграли со бесконечна горна граница

Значи, пишувањето неправилен интеграл се разликува од вообичаениот дефинитивен интеграл по тоа што горната граница на интеграцијата е бесконечна.

Дефиниција. Несоодветен интеграл со бесконечна горна граница на интеграција на континуирана функција ѓ(x) во интервалот од а пред ∞ се нарекува граница на интегралот на оваа функција со горната граница на интеграција б и долната граница на интеграција а под услов горната граница на интеграција да расте без ограничување, т.е.

.

Ако оваа граница постои и е еднаква на некој број наместо бесконечност, тогаш неправилниот интеграл се нарекува конвергентен, а како вредност се зема бројот на кој лимитот е еднаков. Во спротивно неправилниот интеграл се нарекува дивергентени не му се припишува никакво значење.

Пример 1. Пресметај неправилен интеграл(ако се конвергира).

Решение. Врз основа на дефиницијата за неправилен интеграл, наоѓаме

Бидејќи границата постои и е еднаква на 1, тогаш ова неправилен интеграл конвергираи е еднакво на 1.

Во следниот пример, интеграндот е речиси ист како во примерот 1, само степенот x не е два, туку буквата алфа, а задачата е да се проучи неправилниот интеграл за конвергенција. Односно, останува да се одговори на прашањето: при кои вредности на алфа се спојува овој несоодветен интеграл и во кои вредности се разминува?

Пример 2. Испитајте го неправилниот интеграл за конвергенција(долната граница на интеграција е поголема од нула).

Решение. Ајде прво да го претпоставиме тоа, тогаш

Во добиениот израз, се движиме до границата на:

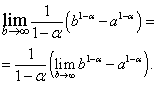
Лесно е да се види дека границата на десната страна постои и е еднаква на нула кога, односно, и не постои кога, т.е.

Во првиот случај, односно кога . Ако тогаш и не постои.

Заклучокот на нашата студија е следниот: ова неправилен интеграл конвергирана и се разминуваво .

Примена на формулата Њутн-Лајбниц за типот на неправилен интеграл што се проучува , можете да ја изведете следната формула, која е многу слична на неа:

.

Ова е генерализирана формула на Њутн-Лајбниц.

Пример 3. Пресметај неправилен интеграл(ако се конвергира).

Границата на овој интеграл постои:

Вториот интеграл, составен збир што го изразува оригиналниот интеграл:

Границата на овој интеграл исто така постои:

.

Го наоѓаме збирот на два интеграли, што е и вредноста на оригиналниот неправилен интеграл со две бесконечни граници:

Неправилни интеграли од втор вид - од неограничени функции и нивна конвергенција

Нека функцијата ѓ(x) дадена на сегментот од а пред б и е неограничен на него. Да претпоставиме дека функцијата оди до бесконечност во точката б , додека во сите други точки од отсечката е континуирана.

Дефиниција. Несоодветен интеграл на функција ѓ(x) на сегментот од а пред б се нарекува граница на интегралот на оваа функција со горната граница на интеграција в , ако кога се стремиме в До б функцијата се зголемува без ограничување, и во точка x = б функцијата не е дефинирана, т.е.

.

Ако оваа граница постои, тогаш неправилниот интеграл од вториот вид се нарекува конвергентен, во спротивно се нарекува дивергентен.

Користејќи ја формулата Њутн-Лајбниц, изведуваме.

1. Неправилни интеграли со бесконечни граници

Да се ​​потсетиме на дефиницијата за интеграл како граница на интегрални збирови:

Дефиницијата претпоставува дека интервалот на интеграција е конечен, а функцијата f(x) е континуирана во него. Прекршувањето на овие претпоставки доведува до неправилни интеграли.

Дефиниција.Ако интегралот се стреми кон конечна граница додека се зголемува бесконечно "б", тогаш оваа граница се нарекува неправилен интеграл со бесконечна горна граница на функцијата f (x) и се означува со симболот

Во овој случај, несоодветниот интеграл се вели дека постои или се спојува.

Ако одредената граница не постои или постои, но е бесконечна, тогаш се вели дека интегралот не постои или дека се разминува.

Несоодветен интеграл со бесконечна долна граница е дефиниран слично:

Неправилен интеграл со две бесконечни граници е даден со:

каде што c е која било фиксна точка на оската Ox.

Значи, неправилните интеграли може да имаат бесконечна долна граница, бесконечна горна граница, а исто така и две бесконечни граници.

Знаци на конвергенција. Апсолутна и условна конвергенција

Интеграл постои само ако постои секој од интегралите: и .

Пример.Испитајте ја конвергенцијата на интегралот

Претпоставувајќи c = 0, добиваме:

тие. интегралот конвергира.

Понекогаш нема потреба да се пресметува несоодветен интеграл, туку доволно е само да се знае дали тој конвергира или дивергира споредувајќи го со друг интеграл.

Споредбена теорема за неправилни интеграли.

Нека функцијата f (x) во интервалот има неколку (конечен број) точки на дисконтинуитет од првиот вид, оваа „пречка“ може лесно да се елиминира со делење на отсечката на неколку отсечки со точки на дисконтинуитет, пресметување дефинитивни интеграли на секој поединечен дел и собирање на резултатите.

Да го разгледаме дефинитивниот интеграл на функција која е неограничена кога се приближува до еден од краевите на сегментот, на пример, .

(Во такви случаи тие обично велат: ''Функцијата има бесконечен дисконтинуитет на десниот крај на интервалот на интеграција.'').

Јасно е дека вообичаената дефиниција за интеграл овде го губи своето значење.

Дефиниција. Неправилен интеграл на функцијата f(x), континуиран за £ x< b и неограниченной при x ® b - 0, называется предел:

Неправилниот интеграл на функција која има бесконечен дисконтинуитет на левиот крај од сегментот е дефиниран слично:

Следствено, во делот [-1, 0] интегралот се разминува.

Ова значи дека интегралот се разминува и во делот.

Така, овој интеграл се разминува во текот на целиот интервал [-1, 1]. Забележете дека ако почнеме да го пресметуваме овој интеграл без да внимаваме на дисконтинуитетот на интеградот во точката x = 0, ќе добиеме неточен резултат. Навистина,

, што е невозможно.

Значи, за да се проучи неправилниот интеграл на дисконтинуирана функција, потребно е да се „подели“ на неколку интеграли и да се проучат.

Ако интеграндот има дисконтинуитет од вториот вид на (конечниот) интервал на интеграција, зборуваме за несоодветен интеграл од вториот вид.

10.2.1 Дефиниција и основни својства

Дозволете ни да го означиме интервалот на интеграција со $\left[a, \, b \right ]$; двата од овие броеви се претпоставуваат дека се конечни подолу. Ако има само 1 дисконтинуитет, тој може да се наоѓа или во точката $a$ или во точката $b$, или во интервалот $(a,\,b)$. Прво да го разгледаме случајот кога има дисконтинуитет од вториот вид во точката $a$, а во други точки функцијата интегранд е континуирана. Значи разговараме за интегралот

\почеток(равенка) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(равенка)

и $f(x) \rightarrow \infty $ кога $x \rightarrow a+0$. Како и досега, првото нешто што треба да направите е да му дадете значење на овој израз. За да го направите ова, разгледајте го интегралот

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

Дефиниција. Нека има конечна граница

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

Тогаш се вели дека неправилниот интеграл од вториот вид (22) се конвергира и вредноста $A$ му е доделена; самата функција $f(x)$ се вели дека е интеграбилна на интервалот $\left[a, \ , b\десно]$.

Да ја разгледаме опцијата кога има дисконтинуитет од вториот вид во функцијата интегранд на горната граница на интервалот на интеграција. Овој случај може да се сведе на претходниот со правење промена на променливата $x=-t$ и потоа преуредување на границите на интеграција.

Да ја разгледаме опцијата кога функцијата интегранд има дисконтинуитет од вториот вид во интервалот на интеграција, во точката $c \in (a,\,b)$. Во овој случај, оригиналниот интеграл

\почеток(равенка) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(равенка)

претставен како збир

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Дефиниција. Ако двата интеграли $I_1, \, I_2$ се спојуваат, тогаш неправилниот интеграл (23) се нарекува конвергентен и му се доделува вредност еднаква на збирот на интегралите $I_1, \, I_2$, функцијата $f(x)$ се нарекува интеграбилен на интервалот $\left [a, \, b\right]$. Ако барем еден од интегралите $I_1,\, I_2$ е дивергентен, неправилниот интеграл (23) се нарекува дивергентен.

Конвергентни неправилни интеграли од вториот вид ги имаат сите стандардни својства на обичните определени интеграли.

1. Ако $f(x)$, $g(x)$ се интегрирани на интервалот $\left[ a, \,b \right ]$, тогаш нивниот збир $f(x)+g(x)$ е исто така може да се интегрира на овој интервал, и \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Ако $f(x)$ може да се интегрира на интервалот $\left[ a, \, b \right ]$, тогаш за која било константа $C$ функцијата $C\cdot f(x)$ е исто така интеграбилна на овој интервал, и \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Ако $f(x)$ може да се интегрира на интервалот $\left[ a, \, b \right ]$, и на овој интервал $f(x)>0$, тогаш \[ \int _a^ (б ) f(x)dx\,>\,0. \] 4. Ако $f(x)$ може да се интегрира на интервалот $\left[ a, \, b \right ]$, тогаш за кој било $c\in (a, \,b)$ интегралите \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] исто така конвергираат, и \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (адитивност на интегралот во текот на интервалот).

Размислете за интегралот

\begin(равенка) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end (равенка)

Ако $k>0$, интеграндот има тенденција на $\infty$ како $x \rightarrow +0$, така што интегралот е несоодветен од вториот вид. Ајде да ја претставиме функцијата

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

Во овој случај антидеривативот е познат, па

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

за $k \neq 1$,

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

за $k = 1$. Со оглед на однесувањето на $\epsilon \rightarrow +0$, доаѓаме до заклучок дека интегралот (20) конвергира на $k

10.2.2 Тестови за конвергенција на неправилни интеграли од втор вид

Теорема (првиот знак за споредба). Нека $f(x)$, $g(x)$ се континуирани за $x\in (a,\,b)$ и $0 1. Ако интегралот \[ \int _a^(b)g(x) dx \] конвергира, потоа интегралот \[ \int _a^(b)f(x)dx конвергира. \] 2. Ако интегралот \[ \int _a^(b)f(x)dx \] дивергира, тогаш интегралот \[ \int _a^(b)g(x)dx дивергира. \]

Теорема (втор споредбен критериум). Нека $f(x)$, $g(x)$ се континуирани и позитивни за $x\in (a,\,b)$, и нека има конечна граница

\[ \theta = \lim_(x \десна стрелка a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Потоа интегралите

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

се спојуваат или се разминуваат истовремено.