Што е равенка?

Оние кои ги прават првите чекори во алгебрата, се разбира, бараат најуредена презентација на материјалот. Затоа, во нашата статија за тоа што е равенка, не само што ќе дадеме дефиниција, туку и ќе дадеме различни класификации на равенки со примери.

Што е равенка: општи поими

Значи, равенката е вид на еднаквост со непозната, означена со латинска буква. Во овој случај, нумеричката вредност на оваа буква, која ни овозможува да ја добиеме точната еднаквост, се нарекува корен на равенката. Повеќе за ова можете да прочитате во нашата статија, но ние ќе продолжиме да зборуваме за самите равенки. Аргументите на равенката (или променливите) се непознати, а решението на равенката е наоѓање на сите нејзини корени или отсуство на корени.

Видови равенки

Равенките се поделени во две големи групи: алгебарски и трансцендентални.

• Алгебарска равенка е онаа во која се користат само алгебарски операции за да се најде коренот на равенката - 4 аритметички, како и степенување и извлекување на природниот корен.
• Трансцендентална равенка е равенка во која неалгебарските функции се користат за да се најде коренот: на пример, тригонометриски, логаритамски и други.

Меѓу алгебарските равенки има и:

• цели броеви - при што двата дела се состојат од цели алгебарски изрази во однос на непознати;
• фракционо - што содржи целобројни алгебарски изрази во броител и именител;
• ирационални - алгебарски изрази овде се под знакот на коренот.

Забележете исто така дека фракционите и ирационалните равенки може да се сведат на решавање на цели равенки.

Трансценденталните равенки се поделени на:

• Експоненцијалните равенки се равенки кои содржат променлива како експонент. Тие се решаваат со преместување на една основа или експонент, вадење на заедничкиот фактор од загради, факторинг и некои други методи;
• логаритамски - равенки со логаритми, односно равенки каде што непознатите се внатре во самите логаритми. Решавањето на такви равенки е многу тешко (за разлика од, да речеме, повеќето алгебарски), бидејќи за ова е потребна солидна математичка обука. Овде најважно е да се премине од равенка со логаритми во равенка без нив, односно да се поедностави равенката (овој метод на отстранување на логаритми се нарекува потенцирање). Се разбира, можно е да се потенцира логаритамската равенка само ако тие имаат идентични нумерички основи и немаат коефициенти;
• тригонометриските равенки се равенки со променливи под знаците на тригонометриските функции. Нивното решение бара првично совладување на тригонометриските функции;
• измешани се диференцирани равенки со делови кои припаѓаат на различни типови (на пример, со параболични и елиптични делови или елиптични и хиперболични итн.).

Што се однесува до класификацијата по бројот на непознати, сè е едноставно: се разликуваат равенки со една, две, три и така натаму непознати. Постои и друга класификација, која се заснова на степенот што е на левата страна на полиномот. Врз основа на ова, се разликуваат линеарни, квадратни и кубни равенки. Линеарните равенки може да се наречат и равенки од 1-ви степен, квадратни - 2-ри и кубни, соодветно, 3-ти. Па, сега да дадеме примери на равенки на една или друга група.

Примери на различни видови равенки

Примери на алгебарски равенки:

• секира + b= 0
• секира 3 + bx 2 + cx+ d= 0
• секира 4 + bx 3 + cx 2 + bx + a= 0
  (а не е еднакво на 0)

Примери на трансцендентални равенки:

• cos x = x log x = x−5 2 x = logx+x 5 +40

Примери на цели равенки:

• (2+x)2 = (2+x)(55x-4) (x2-12x+10)4 = (3x+10)4 (4x2+3x-10)2=9x4

Пример за дробни равенки:

• 15 x + — = 5x - 17 x

Пример за ирационални равенки:

• √2kf(x)=g(x)

Примери на линеарни равенки:

• 2x+7=0 x - 3 = 2 - 4x 2x+3=5x+5 - 3x - 2

Примери на квадратни равенки:

• x 2 +5x−7= 0 3x 2 +5x−7= 0 11x 2 −7x+3 = 0

Примери на кубни равенки:

• x 3 -9x 2 -46x+120=0 x 3 - 4x 2 + x + 6 = 0

Примери на експоненцијални равенки:

• 5 x+2 = 125 3 x 2 x = 8 x+3 3 2x +4 3 x -5 = 0

Примери на логаритамски равенки:

• лог 2 x= 3 лог 3 x= -1

Примери на тригонометриски равенки:

• 3sin 2 x + 4sin x cosx + cos 2 x = 2 sin(5x+π/4) = ctg(2x-π/3) sinx + cos 2 x + tan 3 x = ctg 4 x

Примери на мешани равенки:

• log x (log 9 (4⋅3 x −3))=1 |5x−8|+|2⋅5x+3|=13

Останува да се додаде дека се користат различни методи за решавање на равенки од различни типови. Па, за да ги решите речиси сите равенки, ќе ви треба знаење не само за алгебра, туку и за тригонометрија, а често и многу длабоко знаење.

Математика. Алгебра. Геометрија. Тригонометрија

АЛГЕБРА: Равенки и системи на равенки

4.2. Видови равенки и методи за нивно решавање

Во случај кога е неопходно да се најдат вредностите на променливата што ги задоволуваат двете дадени равенки, велиме дека е дадена, систем на равенки. Кадрава заграда се користи за означување на систем:

Неколку равенки со една променлива форма збир на равенки, ако задачата е да се најдат сите такви вредности на променливата, од кои секоја е коренот на барем една од овие равенки. Квадратна заграда се користи за означување на популација:

Равенки кои содржат променлива под знакот на модул.

Апсолутната вредност на некој број Асе дефинира на следниов начин:

Пример: Решете ја равенката

.

Решение: ако

, Тоа . Можете да го напишете вака:

Од равенството.

ние најдовме X= -9. Меѓутоа, со оваа вредност на променливата, нееднаквоста не важи, што значи дека пронајдената вредност не е коренот на оваа равенка., Тоа и оваа равенка ќе има форма. Можете да го напишете вака:

Од равенството.

ние најдовме . Нееднаквоста е вистина, што значи - коренот на оваа равенка..

Равенки со променлива во именителот.

Размислете за равенките на формата

. (1)

Решението на равенката од типот (1) се заснова на следново тврдење: дропка е еднаква на 0 ако и само ако нејзиниот броител е еднаков на 0, а неговиот именител не е нула.

Во согласност со горенаведеното, решението на равенката

се изведува во две фази: прво треба да ја решите равенката, а потоа дознајте дали со пронајдените вредности на променливата, Xименителна 0. Ако q(x) ¹ 0 , потоа пронајдениот корен на равенкатае исто така коренот на равенката (1); Акоq(x) = 0, потоа добиениот корен од равенкатае и коренот на равенката (1). Резултирачкиот систем е:

Домен на равенката

f(x) = g(x) повикајте го множеството од сите тие вредности на променливата X, за што изразотf(x), и изразот g(x)има смисла.

Ако во процесот на трансформација на равенката се прошири нејзиниот домен на дефиниција, тогаш може да се појават необични корени. Затоа, сите пронајдени вредности на променливата мора да се проверат со замена во оригиналната равенка или со користење на доменот на дефиниција на оригиналната равенка.

Рационални равенки.

Равенката

f(x) = g(x) повикани рационален, Ако f(x) и g(x)-рационални изрази. Покрај тоа, ако f(x) и g(x)- цели изрази, тогаш се повикува равенката целина ;ако барем еден од изразитеf(x), g(x)е фракционална, тогаш рационалната равенкаf(x) = g(x) повикани фракционо .

За да решите рационална равенка, потребно е:

1. најдете заеднички именител на сите достапни дропки;
2. заменете ја оваа равенка со цела, множејќи ги двата нејзини дела со заеднички именител;
3. Решете ја добиената цела равенка;
4. Исфрлете ги од своите корени оние што прават да исчезне заедничкиот именител.

Решавање на равенката

p(x) = 0 метод на факторизација. p(x) може да се факторизира: , потоа равенкатазема форма . Ако А- корен на равенката, Тоа , затоа барем еден од броевитее еднакво на 0.

Исто така важи и спротивното: ако X

= А- коренот на барем една од равенките, , , Тоа А- корен на равенката. Тоа е

Решавање равенки

со воведување на нова променлива.

Дозволете ни да ја објасниме суштината на методот со пример.

Пример: Решете ја равенката

.

Решение.Да ставиме

, ја добиваме равенката, каде што наоѓаме . Проблемот се сведува на решавање на множество равенки

Û

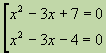
Првата квадратна равенка нема вистински корени, така што нејзината дискриминантна е негативна. Од вториот наоѓаме

. Ова се корените на дадената равенка.

Равенката на формата се нарекува биквадратична

, Каде А ¹ 0. Биквадратната равенка се решава со воведување на нова променлива:ставање , доаѓаме до квадратната равенка .

Ирационални равенки.

Ирационално

е равенка во која променливата е содржана под знакот на коренот или под знакот на подигање до фракциона моќ. Еден метод за решавање на такви равенки е методот на подигање на двете страни на равенката на иста моќност:

А) трансформирајте ја дадената ирационална равенка во форма:

;

Б) ги подигаме двете страни на добиената равенка на

n-ти степен:

;

Б) со оглед на тоа

, ја добиваме равенката

f(x) = g(x);

)Ја решаваме равенката и правиме проверка, бидејќи подигањето на двете страни на равенката на рамномерна моќност може да доведе до појава на надворешни корени. Оваа проверка се врши со замена на пронајдените вредности на променливата во оригиналната равенка.

Авторски права © 2005-2013 Xenoid v2.0

Употребата на материјали на страницата е можна со активна врска.

Одржувањето на вашата приватност е важно за нас. Поради оваа причина, развивме Политика за приватност која опишува како ги користиме и складираме вашите информации. Ве молиме прегледајте ги нашите практики за приватност и кажете ни ако имате какви било прашања.

Собирање и користење на лични информации

Личните информации се однесуваат на податоци што може да се користат за идентификување или контактирање на одредена личност.

Може да биде побарано од вас да ги дадете вашите лични податоци во секое време кога ќе не контактирате.

Подолу се дадени неколку примери за типовите на лични информации што можеме да ги собираме и како можеме да ги користиме тие информации.

Кои лични податоци ги собираме:

• Кога поднесувате апликација на страницата, може да собереме различни информации, вклучувајќи го вашето име, телефонски број, адреса на е-пошта итн.

Како ги користиме вашите лични податоци:

• Личните информации што ги собираме ни овозможуваат да ве контактираме со уникатни понуди, промоции и други настани и претстојни настани.
• Од време на време, може да ги користиме вашите лични податоци за да испраќаме важни известувања и комуникации.
• Може да користиме и лични информации за внатрешни цели, како што се спроведување ревизии, анализа на податоци и разни истражувања со цел да ги подобриме услугите што ги обезбедуваме и да ви дадеме препораки во врска со нашите услуги.
• Ако учествувате во наградно извлекување, натпревар или слична промоција, ние може да ги користиме информациите што ги давате за администрирање на такви програми.

Откривање на информации на трети страни

Ние не ги откриваме информациите добиени од вас на трети страни.

Исклучоци:

• Доколку е потребно - во согласност со закон, судска процедура, во правни постапки и/или врз основа на јавни барања или барања од владини органи на територијата на Руската Федерација - да ги откриете вашите лични податоци. Ние, исто така, може да откриеме информации за вас ако утврдиме дека таквото откривање е неопходно или соодветно за безбедност, спроведување на законот или други цели од јавна важност.
• Во случај на реорганизација, спојување или продажба, можеме да ги пренесеме личните информации што ги собираме на соодветната трета страна наследник.

Заштита на лични информации

Преземаме мерки на претпазливост - вклучувајќи административни, технички и физички - за да ги заштитиме вашите лични информации од губење, кражба и злоупотреба, како и од неовластен пристап, откривање, менување и уништување.

Почитување на вашата приватност на ниво на компанија

За да се осигураме дека вашите лични информации се безбедни, ние ги пренесуваме стандардите за приватност и безбедност на нашите вработени и строго ги спроведуваме практиките за приватност.

Видови алгебарски равенки и методи за нивно решавање

За студентите заинтересирани за математика, при решавање на алгебарски равенки од повисоки степени, ефективен метод за брзо наоѓање корени, делење со остаток со биномот x -  или со секира + b, е Хорнеровата шема.

Размислете за шемата на Хорнер.

Да го означиме нецелосниот количник при делење на P(x) со x –  преку

Q (x) = b 0 x n -1 + b 1 x n -2 + ... + b n -1, а остатокот е b n.

Бидејќи P(x) = Q (x)(x–) + b n, тогаш важи еднаквоста

а 0 x n + а 1 x n -1 + … + а n = (b 0 x n -1 + b 1 x n -2 + … + b n -1)(х–) + b n

Ајде да ги отвориме заградите од десната страна и да ги споредиме коефициентите за истите сили на x лево и десно. Добиваме дека a 0 = b 0 и за 1  k  n важат односите a k = b k -  b k -1. Следи дека b 0 = a 0 и b k = a k +  b k -1, 1  k  n.

Пресметувањето на коефициентите на полиномот Q (x) и остатокот b n го пишуваме во форма на табела:

а 0

а 1

а 2

А n-1

А n

b 0 = a 0

b 1 = a 1 +  b 0

b 2 = a 2 +  b 1

b n-1 = a n-1 +  b n-2

b n = a n +  b n-1

Пример 1. Полиномот 2x 4 – 7x 3 – 3x 2 + 5x – 1 поделете го со x + 1.

Решение. Ја користиме шемата на Хорнер.

При делење 2x 4 – 7x 3 – 3x 2 + 5x – 1 со x + 1 добиваме 2x 3 – 9x 2 + 6x – 1

Одговор: 2 x 3 – 9x 2 + 6x – 1

Пример 2. Пресметај P(3), каде што P(x) = 4x 5 – 7x 4 + 5x 3 – 2x + 1

Решение. Користејќи ја теоремата на Безут и шемата на Хорнер, добиваме:

Одговор: P(3) = 535

Вежбајте

Користејќи го Хорнеровиот дијаграм, поделете го полиномот

4x 3 – x 5 + 132 – 8x 2 на x + 2;

2) Поделете го полиномот

2x 2 – 3x 3 – x + x 5 + 1 на x + 1;

3) Најдете ја вредноста на полиномот P 5 (x) = 2x 5 – 4x 4 – x 2 + 1 за x = 7.

1.1. Наоѓање рационални корени на равенки со целобројни коефициенти

Методот за пронаоѓање на рационални корени на алгебарска равенка со целобројни коефициенти е даден со следнава теорема.

Теорема:Ако равенката со целобројни коефициенти има рационални корени, тогаш тие се количник на делење на делителот на слободниот член со делителот на водечкиот коефициент.

Доказ: a 0 x n + a 1 x n -1 + … + a n = 0

Нека x = p/ q е рационален корен, q, p се копромиум.

Заменувајќи ја дропката p/q во равенката и ослободувајќи се од именителот, добиваме

а 0 р n + a 1 p n -1 q + … + a n -1 pq n -1 + a n q n = 0 (1)

Ајде да го преработиме (1) на два начина:

a n q n = р(– а 0 р n -1 – а 1 р n -2 q – … – а n -1 q n -1) (2)

а 0 р n = q (– а 1 р n -1 –… – а n -1 рq n -2 – а n q n -1) (3)

Од еднаквоста (2) следува дека a n q n е делив со p, и бидејќи q n и p се сопрост, тогаш a n се дели со p. Слично, од еднаквоста (3) следува дека 0 е делив со q. Теоремата е докажана.

Пример 1. Решете ја равенката 2x 3 – 7x 2 + 5x – 1 = 0.

Решение. Равенката нема целобројни корени, ги наоѓаме рационалните корени на равенката. Нека нередуцираната дропка p /q е коренот на равенката, тогаш p се наоѓа меѓу делителите на слободниот член, т.е. меѓу броевите  1, а q меѓу позитивните делители на водечкиот коефициент: 1; 2.

Оние. рационалните корени на равенката мора да се бараат меѓу броевите  1,  1/2, означете P 3 (x) = 2x 3 – 7x 2 + 5x – 1, P 3 (1)  0, P 3 (–1)  0,

P 3 (1/2) = 2/8 – 7/4 + 5/2 – 1 = 0, 1/2 е коренот на равенката.

2x 3 – 7x 2 + 5x – 1 = 2x 3 – x 2 – 6 x 2 + 3x + 2x – 1 = 0.

Добиваме: x 2 (2x – 1) – 3x (2x – 1)+ (2x – 1) = 0; (2x – 1) (x 2 – 3x + 1) = 0.

Со изедначување на вториот фактор на нула и решавање на равенката, добиваме

Одговор:
,

Вежби

Решавање на равенки:

6x 3 – 25x 2 + 3x + 4 = 0;

6x 4 – 7x 3 – 6x 2 + 2x + 1 = 0;

3x 4 – 8x 3 – 2x 2 + 7x – 1 = 0;

1.2. Реципрочни равенки и методи на решение

Дефиниција.Равенката со целобројни сили во однос на непозната се нарекува реципрочна ако нејзините коефициенти, еднакво оддалечени од краевите на левата страна, се еднакви еден со друг, т.е. равенка на формата

А x n + bx n -1 + cx n -2 + … + cx 2 + bx + a = 0

Реципрочна равенка на непарен степен

А x 2 n +1 + bx 2 n + cx 2 n -1 + … + cx 2 + bx + a = 0

секогаш има корен x = – 1. Затоа, тоа е еквивалентно на комбинирање на равенката x + 1 = 0 и  x 2 n +  x 2 n -1 + … +  x +  = 0. Последната равенка е реципрочна равенка од парен степен. Така, решавањето на реципрочни равенки од кој било степен се сведува на решавање на реципрочна равенка од парен степен.

Како да се реши? Нека е дадена реципрочна равенка со парен степен

А x 2 n + bx 2 n -1 + … + dx n +1 + ex n + dx n -1 + … + bx + a = 0

Забележете дека x = 0 не е корен од равенката. Потоа ја делиме равенката со x n, добиваме

А x n + bx n -1 + … + dx + e + dx -1 + … + bx 1- n + аx -n = 0

Условите од левата страна ги групираме во парови

А( x n + x - n ) + b (x n -1 + x -(n -1) + … + d(x + x -1) + e = 0

Ја правиме замената x + x -1 = y. По замена на изразите x 2 + x -2 = y 2 – 2;

x 3 + x -3 = y 3 – 3y; x 4 + x -4 = y 4 – 4y + 2 во равенката ја добиваме равенката за наАу n + Со n -1 +Cy n -2 + … + Ey + D = 0.

За да ја решите оваа равенка, треба да решите неколку квадратни равенки од формата x + x -1 = y k, каде k = 1, 2, ... n. Така, ги добиваме корените на првобитната равенка.

Пример 1. Решете ја равенката x 7 + x 6 – 5x 5 – 13x 4 – 13x 3 – 5x 2 + 2x + 1 = 0.

Решение. x = – 1 е коренот на равенката. Ајде да ја примениме шемата на Хорнер.

Нашата равенка ќе ја има формата:

(x + 1) (x 6 + x 5 - 6x 4 - 7x 3 - 6x 2 + x + 1) = 0

1) x + 1 = 0, x = -1;

2) x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1 = 0 | : x 3  0; x 3 + x 2 – 6x – 7 – 6/x + 1/x 2 + 1/x 3 =0.

Со групирање добиваме: .

Ајде да воведеме замена:
;
;
.

Добиваме релативно наравенка: y 3 – 3y + y 2 – 2 – 6y – 7 = 0;

y 3 + y 2 – 9y – 9 = 0; y 2 (y + 1) – 9 (y + 1) = 0; (y + 1) (y 2 – 9); y 1 = -1, y 2,3 =  3.

Решавање равенки
,
,
,

ги добиваме корените:
,
,
,

Одговор: x 1 = -1,
,

Вежби

Решавајте равенки.

2x 5 + 5x 4 – 13x 3 – 13x 2 + 5x + 2 = 0;

2x 4 + 3x 3 – 16x 2 + 3x + 2 = 0;

15x 5 + 34x 4 + 15x 3 – 15x 2 – 34x – 15 = 0.

1.3. Метод на замена на променлива за решавање равенки

Методот на замена на променливата е најчестиот метод. Уметноста на правење променлива промена е да се види која промена има најмногу смисла и побрзо ќе доведе до успех.

Ако е дадена равенката

F(f(x)) = 0, (1)

тогаш со замена на непознатата y = f (x) прво се сведува на равенката

F(y) = 0, (2)

а потоа по наоѓањето на сите решенија на равенката (2) y 1, y 2, ..., y n, ... се сведува на решавање на множеството равенки f (x) = y 1, f (x) = y 2 ,..., f (x) = y 2,...

Главните начини за спроведување на методот за замена на променливи се:

користење на основното својство на дропка;

истакнување на квадратот на биномот;

транзиција кон систем на равенки;

отворање загради во парови;

отворање на загради во парови и делење на двете страни на равенката;

намалување на степенот на равенката;

двојна замена.

1.3.1. Намалување на моќта на равенката

Решете ја равенката (x 2 + x + 2) (x 2 + x + 3) = 6 (3)

Решение. Да означиме x 2 + x + 2 = y, а потоа да земеме y (y + 1) = 6, решавајќи го последното, добиваме y 1 = 2, y 2 = -3. Оваа равенка (3) е еквивалентна на множеството равенки x 2 + x + 2 = 2

x 2 + x + 2 = -3

Решавајќи го првото, добиваме x 1 = 0, x 2 = -1. Решавајќи го второто, добиваме
,

Одговор: x 1 = 0, x 2 = -1,

1.3.2. Четвртостепена равенка од формата (x + a)(x +б )(x + в )(x + г ) = м , каде што a + b = c + d, или a + c = b + d, или a + d = b + c.

Пример. Решете ја равенката (x - 1) (x - 7) (x -4) (x + 2) = 40

Решение. – 1- 4 = - 7 + 2, - 5 = - 5, множејќи ги овие парови загради, ја добиваме равенката (x 2 - 5x - 14)(x 2 - 5x + 4) = 40

Да ја воведеме замената: x 2 - 5x – 14 = y, ја добиваме равенката y(y + 18) = 40, y 2 + 18y = 40, y 2 + 18y – 40 = 0. y 1 = -20, y 2 = 2. Враќајќи се на оригиналната променлива, решаваме множество равенки:

X 2 - 5x – 14 = - 20 x 1 = 2; x 2 = 3

x 2 - 5x – 14 = 2 x 3,4 =

Одговор: x 1 = 2; x 2 = 3 x 3,4 =

1.3.3. Равенка од формата (x + a)(x + b)(x + c)(x + d) = Ex 2,

Каде ab = cd, или ac =bd, или ad = bc. Отворете ги заградите во парови и поделете ги двата дела со x 2  0.

Пример. (x - 1) (x - 2) (x - 8) (x - 4) = 4x 2

Решение. Производот на броевите во првата и третата и во втората и четвртата заграда се еднакви, т.е. – 8 (- 1) = (- 2)(- 4). Да ги помножиме наведените парови загради и да ја напишеме равенката (x 2 - 9x + 8)(x 2 - 6x + 8) = 4x 2.

Бидејќи x = 0 не е корен на равенката, ние ги делиме двете страни на равенката со x 2  0, добиваме:
, замена:
, оригиналната равенка ќе ја има формата:т(т+3) =4, т 2 + 3 т=4, т 2 + 3 т – 4=0, т 1 =1, т 2 = - 4.

Да се ​​вратиме на оригиналната променлива:

x 2 - 10x + 8 = 0

x 2 - 5x + 8 = 0

Ја решаваме првата равенка, добиваме x 1,2 = 5 

Втората равенка нема корени.

Одговор: x 1,2 = 5 

1.3.4. Равенка од четвртиот тип (ax 2 + b 1 x + c)(a x 2 + b 2 x + c) = A x 2

Равенка (секира 2 + б 1 x+ в)(а x 2 + б 2 x + в) = А x 2, каде што в  0, А  2
, кој по замена на непознатото
може да се препише како квадрат и лесно да се реши.

Пример. (x 2 + x+ 2) (x 2 + 2x + 2) = 2x 2

Решение. Лесно е да се види дека x = 0 не е корен на оваа равенка со делење на оваа равенка со x 2 , ја добиваме равенката

замена
, ја добиваме равенката (y+1)(y+2) = 2, решавајќи ја, имаме корени y 1 = 0; во 2 = - 3, затоа првобитната равенка е еквивалентна на множеството равенки

решавајќи, добиваме x 1 = -1; x 2 = -2.

Одговор: x 1 = -1; x 2 = -2

1.3.5. Равенка на формата: a (cx 2 + p 1 x + q) 2 + b (cx 2 + p 2 x + q) 2 = Ax 2

Равенката а(cx 2 + стр 1 x + q) 2 + б(cx 2 + стр 2 x + q) 2 = Секира 2 каде а, б, в, q, Асе такви што q 0, А 0, в 0, а 0, б 0 нема корен x = 0, така што равенката се дели со x 2 , добиваме еквивалентна равенка
, кој по замената
може да се препише како квадратна равенка која лесно може да се реши. + 1)( x 2 – 14x + 15 = 0

x 2 – 7 x + 15 = 0

Одговор:

Во некои проблеми на физиката, не е можно да се воспостави директна врска помеѓу количините што го опишуваат процесот. Но, можно е да се добие еднаквост што ги содржи дериватите на функциите што се проучуваат. Така произлегуваат диференцијалните равенки и потребата од нивно решавање за да се најде непозната функција.

Оваа статија е наменета за оние кои се соочуваат со проблем за решавање на диференцијална равенка во која непознатата функција е функција на една променлива. Теоријата е структурирана на таков начин што со нула познавање на диференцијални равенки, можете да се справите со вашата задача.

Секој тип на диференцијални равенки е поврзан со метод на решение со детални објаснувања и решенија за типични примери и проблеми. Сè што треба да направите е да го одредите типот на диференцијалната равенка на вашиот проблем, да пронајдете сличен анализиран пример и да извршите слични дејства.

За успешно решавање на диференцијални равенки, ќе ви треба и способност да најдете множества на антидеривати (неопределени интеграли) од различни функции. Доколку е потребно, препорачуваме да се повикате на делот.

Прво, ќе ги разгледаме типовите на обични диференцијални равенки од прв ред што можат да се решат во однос на изводот, потоа ќе преминеме на ODE од втор ред, потоа ќе се задржиме на равенките од повисок ред и ќе завршиме со системи на диференцијални равенки.

Потсетиме дека ако y е функција од аргументот x.

Диференцијални равенки од прв ред.

Наједноставните диференцијални равенки од прв ред на формата.

Ајде да напишеме неколку примери на таков далечински управувач .

Диференцијални равенки може да се реши во однос на изводот со делење на двете страни на еднаквоста со f(x) . Во овој случај, доаѓаме до равенка која ќе биде еквивалентна на првобитната за f(x) ≠ 0. Примери за такви ODE се .

Ако има вредности на аргументот x на кои функциите f(x) и g(x) истовремено исчезнуваат, тогаш се појавуваат дополнителни решенија. Дополнителни решенија на равенката дадени x се сите функции дефинирани за овие вредности на аргументот. Примери за такви диференцијални равенки вклучуваат:

Диференцијални равенки од втор ред.

Линеарни хомогени диференцијални равенки од втор ред со константни коефициенти.

LDE со константни коефициенти е многу чест тип на диференцијални равенки. Нивното решение не е особено тешко. Прво, се наоѓаат корените на карактеристичната равенка . За различни p и q, можни се три случаи: корените на карактеристичната равенка можат да бидат реални и различни, реални и совпаѓаат или сложени конјугати. Во зависност од вредностите на корените на карактеристичната равенка, општото решение на диференцијалната равенка се запишува како , или , или соодветно.

На пример, разгледајте линеарна хомогена диференцијална равенка од втор ред со константни коефициенти. Корените на неговата карактеристична равенка се k 1 = -3 и k 2 = 0. Корените се реални и различни, затоа, општото решение на LODE со константни коефициенти ја има формата


Линеарни нехомогени диференцијални равенки од втор ред со константни коефициенти.

Општото решение на LDDE од втор ред со константни коефициенти y се бара во форма на збир од општото решение на соодветните LDDE и одредено решение на првобитната нехомогена равенка, односно . Претходниот став е посветен на изнаоѓање на општо решение за хомогена диференцијална равенка со константни коефициенти. И одредено решение се определува или со методот на неопределени коефициенти за одредена форма на функцијата f(x) на десната страна на првобитната равенка, или со методот на менување произволни константи.

Како примери на LDDE од втор ред со константни коефициенти, даваме


За да ја разберете теоријата и да се запознаете со деталните решенија на примери, ви нудиме на страницата линеарни нехомогени диференцијални равенки од втор ред со константни коефициенти.

Линеарни хомогени диференцијални равенки (LODE) и линеарни нехомогени диференцијални равенки (LNDEs) од втор ред.

Посебен случај на диференцијални равенки од овој тип се LODE и LDDE со константни коефициенти.

Општото решение на LODE на одреден сегмент е претставено со линеарна комбинација од две линеарно независни парцијални решенија y 1 и y 2 од оваа равенка, т.е. .

Главната тешкотија лежи токму во изнаоѓање линеарно независни парцијални решенија за диференцијална равенка од овој тип. Вообичаено, одредени решенија се избираат од следниве системи на линеарно независни функции:


Сепак, одредени решенија не се секогаш претставени во оваа форма.

Пример за LOD е .

Општото решение на LDDE се бара во форма , каде што е општото решение на соодветниот LDDE, и е посебното решение на оригиналната диференцијална равенка. Само што зборувавме за негово наоѓање, но може да се одреди со помош на методот на менување произволни константи.

Може да се даде пример за LNDU .

Диференцијални равенки од повисоки редови.

Диференцијални равенки кои овозможуваат намалување по редослед.

Редослед на диференцијална равенка , која не ја содржи саканата функција и нејзините деривати до k-1 ред, може да се намали на n-k со замена на .

Во овој случај, оригиналната диференцијална равенка ќе се сведе на . Откако ќе го најдеме неговото решение p(x), останува да се вратиме на замената и да ја одредиме непознатата функција y.

На пример, диференцијалната равенка по замената ќе стане равенка со раздвојливи променливи, а нејзиниот редослед ќе се намали од трето на прво.