Hva er summen av vinklene? Teorem om summen av vinklene til en trekant. Typer etter vinkelstørrelse

Summen av trekantvinkler– viktig, men nok enkelt tema, som undervises i 7. klasse geometri. Temaet består av et teorem, et kort bevis og flere logiske konsekvenser. Kunnskap om dette emnet hjelper med å løse geometriske problemer under påfølgende studie av emnet.

Teorem - hva er vinklene til en vilkårlig trekant lagt sammen?

Teoremet sier at hvis du tar en hvilken som helst trekant, uansett type, vil summen av alle vinkler alltid være 180 grader. Dette er bevist som følger:

• ta for eksempel trekant ABC, tegn en rett linje gjennom punkt B som ligger på toppen og angi den som "a", rett linje "a" er strengt tatt parallell med siden AC;
• mellom rett linje "a" og sidene AB og BC, er vinkler utpekt, og markerer dem med tallene 1 og 2;
• vinkel 1 regnes som lik vinkel A, og vinkel 2 regnes som lik vinkel C, siden disse vinklene regnes for å ligge på tvers;
• dermed blir summen mellom vinklene 1, 2 og 3 (som er angitt i stedet for vinkel B) gjenkjent som lik den utfoldede vinkelen med toppunktet B - og er 180 grader.

Hvis summen av vinklene angitt med tall er 180 grader, blir summen av vinklene A, B og C gjenkjent som lik 180 grader. Denne regelen gjelder for enhver trekant.

Det som følger av den geometriske teoremet

Det er vanlig å fremheve flere konsekvenser fra teoremet ovenfor.

• Hvis problemet vurderer en trekant med rett vinkel, vil en av vinklene som standard være lik 90 grader, og summen av de spisse vinklene vil også være 90 grader.
• Hvis vi snakker om en rett likebenet trekant, vil dens spisse vinkler, som summerer seg til 90 grader, individuelt være lik 45 grader.
• En likesidet trekant består av tre like vinkler, hver av dem vil være lik 60 grader, og totalt vil de være 180 grader.
• Den ytre vinkelen til en trekant vil være lik summen mellom to indre vinkler som ikke er ved siden av den.

Følgende regel kan utledes: enhver trekant har minst to spisse vinkler. I noen tilfeller består en trekant av tre spisse vinkler, og hvis det bare er to, vil den tredje vinkelen være stump eller rett.

Teorem. Summen av de indre vinklene i en trekant er lik to rette vinkler.

La oss ta en trekant ABC (fig. 208). La oss betegne dens indre vinkler med tallene 1, 2 og 3. La oss bevise at

∠1 + ∠2 + ∠3 = 180°.

La oss tegne gjennom et hjørne av trekanten, for eksempel B, en rett linje MN parallelt med AC.

Ved toppunktet B fikk vi tre vinkler: ∠4, ∠2 og ∠5. Summen deres er en rett vinkel, derfor er den lik 180°:

∠4 + ∠2 + ∠5 = 180°.

Men ∠4 = ∠1 er indre kryssvinkler med parallelle linjer MN og AC og sekant AB.

∠5 = ∠3 - dette er indre kryssvinkler med parallelle linjer MN og AC og sekant BC.

Dette betyr at ∠4 og ∠5 kan erstattes av deres like ∠1 og ∠3.

Derfor er ∠1 + ∠2 + ∠3 = 180°. Teoremet er bevist.

2. Egenskapen til den ytre vinkelen til en trekant.

Faktisk, i trekant ABC (fig. 209) ∠1 + ∠2 = 180° - ∠3, men også ∠ВСD, er den ytre vinkelen til denne trekanten, ikke ved siden av ∠1 og ∠2, også lik 180° - ∠3.

Dermed:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Derfor, ∠1 + ∠2= ∠BCD.

Den avledede egenskapen til den ytre vinkelen til en trekant klargjør innholdet i det tidligere beviste teoremet om den ytre vinkelen til en trekant, som bare sa at den ytre vinkelen til en trekant er større enn hver indre vinkel i en trekant som ikke er ved siden av den; nå er det fastslått at den ytre vinkelen er lik summen av begge de indre vinklene som ikke grenser til den.

3. Egenskap til en rettvinklet trekant med en vinkel på 30°.

La vinkel B i den rette trekanten ACB være lik 30° (fig. 210). Da vil dens andre spisse vinkel være lik 60°.

La oss bevise at ben AC er lik halvparten av hypotenusen AB. La oss strekke benet AC utover toppunktet til den rette vinkelen C og sette til side et segment CM lik segmentet AC. La oss koble punkt M til punkt B. Den resulterende trekanten ВСМ er lik trekant ACB. Vi ser at hver vinkel i trekant ABM er lik 60°, derfor er denne trekanten en likesidet trekant.

Leg AC er lik halve AM, og siden AM er lik AB, vil ben AC være lik halve hypotenusen AB.

Summen av de indre vinklene til en trekant er 180 0. Dette er en av de grunnleggende aksiomene i Euklids geometri. Dette er geometrien skoleelever studerer. Geometri er definert som vitenskapen som studerer de romlige formene til den virkelige verden.

Hva motiverte de gamle grekerne til å utvikle geometri? Behovet for å måle felt, enger - områder av jordens overflate. Samtidig aksepterte de gamle grekerne at jordens overflate var horisontal og flat. Med denne antagelsen i betraktning ble Euklids aksiomer skapt, inkludert summen av de indre vinklene til en trekant på 180 0.

Et aksiom er et forslag som ikke krever bevis. Hvordan skal dette forstås? Det uttrykkes et ønske som passer personen, og så bekreftes det med illustrasjoner. Men alt som ikke er bevist er fiksjon, noe som ikke finnes i virkeligheten.

Ved å ta jordoverflaten horisontalt, aksepterte de gamle grekerne automatisk jordens form som flat, men den er annerledes - sfærisk. Det er ingen horisontale plan eller rette linjer i naturen i det hele tatt, fordi tyngdekraften bøyer rommet. Rette linjer og horisontale plan finnes bare i menneskehjernen.

Derfor er Euklids geometri, som forklarer de romlige formene til den fiktive verden, et simulacrum – en kopi som ikke har noen original.

Et av Euklids aksiomer sier at summen av de indre vinklene til en trekant er 180 0. Faktisk, i virkelig buet rom, eller på jordens sfæriske overflate, er summen av de indre vinklene til en trekant alltid større enn 180 0.

La oss tenke slik. Enhver meridian på kloden skjærer ekvator i en vinkel på 90 0. For å få en trekant, må du flytte en annen meridian bort fra meridianen. Summen av vinklene til trekanten mellom meridianene og siden av ekvator vil være 180 0. Men det vil fortsatt være en vinkel på polet. Som et resultat vil summen av alle vinkler være mer enn 180 0.

Hvis sidene krysser hverandre i en vinkel på 90 0 ved polen, vil summen av de indre vinklene til en slik trekant være 270 0. To meridianer som skjærer ekvator i rette vinkler i denne trekanten vil være parallelle med hverandre, og ved polen som skjærer hverandre i en vinkel på 90 0 vil bli vinkelrette. Det viser seg at to parallelle linjer på samme plan ikke bare krysser hverandre, men kan også være vinkelrette på polen.

Selvfølgelig vil sidene til en slik trekant ikke være rette linjer, men konvekse, og gjenta den sfæriske formen kloden. Men dette er akkurat verdensrommets virkelige verden.

Geometrien til det virkelige rommet, tatt i betraktning dets krumning på midten av 1800-tallet. utviklet av den tyske matematikeren B. Riemann (1820-1866). Men skoleelever blir ikke fortalt om dette.

Så, euklidisk geometri, som har form av jorden som flat med en horisontal overflate, som den faktisk ikke er, er et simulacrum. Nootic er Riemannsk geometri som tar hensyn til krumningen av rommet. Summen av de indre vinklene til trekanten i den er større enn 180 0.

Bevis

La ABC" - vilkårlig trekant. La oss lede gjennom toppen B linje parallelt med linje A.C. (en slik rett linje kalles den euklidiske rette linjen). La oss markere et poeng på det D slik at poengene EN Og D ligge på motsatte sider av en rett linje B.C..Vinkler DBC Og ACB lik som indre tverrliggende liggende dannet av en sekant B.C. med parallelle linjer A.C. Og BD. Derfor er summen av vinklene til en trekant ved toppunktene B Og MED lik vinkel ABD.Summen av alle tre vinklene i en trekant er lik summen av vinklene ABD Og BAC. Siden disse vinklene er indre ensidige for parallelle A.C. Og BD ved sekant AB, da er summen deres 180°. Teoremet er bevist.

Konsekvenser

Av teoremet følger det at enhver trekant har to spisse vinkler. Faktisk, ved å bruke bevis ved selvmotsigelse, la oss anta at trekanten bare har én spiss vinkel eller ingen spisse vinkler i det hele tatt. Da har denne trekanten minst to vinkler, som hver er minst 90°. Summen av disse vinklene er ikke mindre enn 180°. Men dette er umulig, siden summen av alle vinklene i en trekant er 180°. Q.E.D.

Generalisering til simpleks teori

Hvor er vinkelen mellom i- og j-flatene til simpleksen.

Notater

• På en kule overstiger summen av vinklene til en trekant alltid 180°, forskjellen kalles sfærisk overskudd og er proporsjonal med arealet av trekanten.
• I Lobachevsky-planet er summen av vinklene til en trekant alltid mindre enn 180°. Forskjellen er også proporsjonal med arealet av trekanten.

se også

Wikimedia Foundation. 2010.

Se hva "Setningen om summen av vinklene til en trekant" er i andre ordbøker:

Egenskap til polygoner i euklidisk geometri: Summen av vinklene n i en trekant er 180°(n 2). Innhold 1 Bevis 2 Merk ... Wikipedia

Pythagoras teorem er en av de grunnleggende teoremene i euklidisk geometri, som etablerer forholdet mellom sidene i en rettvinklet trekant. Innhold 1 ... Wikipedia

Pythagoras teorem er en av de grunnleggende teoremene i euklidisk geometri, som etablerer forholdet mellom sidene i en rettvinklet trekant. Innhold 1 Utsagn 2 Bevis ... Wikipedia

Cosinussetningen er en generalisering av Pythagoras setning. Kvadraten til en side i en trekant er lik summen av kvadratene av de to andre sidene uten to ganger produktet av disse sidene med cosinus av vinkelen mellom dem. For en plan trekant med sidene a,b,c og vinkel α... ... Wikipedia

Dette begrepet har andre betydninger, se Trekant (betydninger). En trekant (i det euklidiske rom) er geometrisk figur, dannet av tre segmenter som forbinder tre punkter som ikke ligger på samme rette linje. Tre prikker,... ...Wikipedia

Standardnotasjon En trekant er den enkleste polygonen som har 3 hjørner (vinkler) og 3 sider; del av planet avgrenset av tre punkter som ikke ligger på samme linje og tre segmenter som forbinder disse punktene i par. Topppunkter i en trekant ... Wikipedia

Gammel gresk matematiker. Jobbet i Alexandria på 300-tallet. f.Kr e. Hovedverket "Principia" (15 bøker), som inneholder grunnlaget for gammel matematikk, elementær geometri, tallteori, generell teori forhold og metoder for å bestemme arealer og volumer,... ... encyklopedisk ordbok

- (døde mellom 275 og 270 f.Kr.) gammel gresk matematiker. Informasjon om tid og sted for hans fødsel har ikke nådd oss, men det er kjent at Euklid bodde i Alexandria og storhetstiden for hans aktivitet skjedde under Ptolemaios I's regjeringstid i Egypt ... ... Stor encyklopedisk ordbok

Geometri lik euklidisk geometri ved at den definerer bevegelsen til figurer, men skiller seg fra euklidisk geometri ved at ett av dets fem postulater (det andre eller femte) erstattes av dets negasjon. Negasjon av et av euklidiske postulater... ... Colliers leksikon

Triangel . Akutt, stump og rettvinklet trekant.

Ben og hypotenusa. Likebenet og likesidet trekant.

Summen av vinkler i en trekant.

Ytre vinkel til en trekant. Tegn på likhet av trekanter.

Bemerkelsesverdige linjer og punkter i en trekant: høyder, medianer,

halveringslinjer, median e perpendikulære, ortosenter,

tyngdepunkt, sentrum av en omskrevet sirkel, sentrum av en innskrevet sirkel.

Pythagoras teorem. Aspektforhold i en vilkårlig trekant.

Triangel er en polygon med tre sider (eller tre vinkler). Sidene i en trekant er ofte indikert med små bokstaver som tilsvarer de store bokstavene som representerer de motsatte hjørnene.

Hvis alle tre vinklene er spisse (fig. 20), så dette spiss trekant . Hvis en av vinklene er rett(C, fig. 21), det er høyre trekant; sidera, bå danne en rett vinkel kalles bena; sidecmotsatt den rette vinkelen kalles hypotenusen. Hvis en av stumpe vinkler (B, fig. 22), det er stump trekant.


Trekant ABC (fig. 23) - likebent, Hvis to sidene er like (en= c); disse like sidene kalles lateralt, kalles tredjeparten basis triangel. Triangel ABC (fig. 24) – likesidet, Hvis Alle sidene er like (en = b = c). Generelt ( en ≠ b ≠ c) vi har scalene triangel .

Grunnleggende egenskaper ved trekanter. I en hvilken som helst trekant:

1. Motsatt den større siden ligger den større vinkelen, og omvendt.

2. Like vinkler ligger motsatte like sider, og omvendt.

Spesielt alle vinkler inn likesidet trekanten er like.

3. Summen av vinklene i en trekant er 180 º .

Fra de to siste egenskapene følger det at hver vinkel i en likesidet

trekanten er 60 º.

4. Fortsetter en av sidene i trekanten (AC, fig. 25), vi får utvendig

vinkel BCD . Den ytre vinkelen til en trekant er lik summen av de indre vinklene,

ikke ved siden av den : BCD = A + B.

5. Noen siden av en trekant er mindre enn summen av de to andre sidene og større

deres forskjeller (en < b + c, en > b – c;b < en + c, b > en – c;c < en + b,c > en – b).

Tegn på likhet av trekanter.

Trekanter er kongruente hvis de er respektive like:

en ) to sider og vinkelen mellom dem;

b ) to hjørner og siden ved siden av dem;

c) tre sider.

Tegn på likhet av rette trekanter.

To rektangulær trekanter er like hvis en av følgende betingelser er oppfylt:

1) bena deres er like;

2) benet og hypotenusen til en trekant er lik benet og hypotenusen til den andre;

3) hypotenusen og den spisse vinkelen til en trekant er lik hypotenusen og den spisse vinkelen til den andre;

4) benet og den tilstøtende spisse vinkelen til en trekant er lik benet og den tilstøtende spisse vinkelen til den andre;

5) benet og den motsatte spisse vinkelen til en trekant er lik benet og den motsatte spisse vinkelen til den andre.

Fantastiske linjer og punkter i trekanten.

Høyde trekant ervinkelrett,senkes fra et hvilket som helst toppunkt til motsatt side ( eller fortsettelsen). Denne siden kallesbase av trekanten . De tre høydene i en trekant krysser alltid hverandrepå et tidspunkt, kalt ortosenter triangel. Ortosenter av en spiss trekant (punkt O , Fig. 26) er plassert inne i trekanten, ogortosenter av en stump trekant (punkt O , fig. 27) – utenfor; Ortosenteret til en rettvinklet trekant faller sammen med toppunktet til den rette vinkelen.

Median - Dette linjestykke , koble et hvilket som helst toppunkt i en trekant til midten av motsatt side. Tre medianer av en trekant (AD, BE, CF, fig.28) kryss på ett punkt O , alltid liggende inne i trekanten og være hans tyngdepunkt. Dette punktet deler hver median i forholdet 2:1, regnet fra toppunktet.

Bisector - Dette halveringssegment vinkel fra toppunkt til punkt kryss med motsatt side. Tre halveringslinjer i en trekant (AD, BE, CF, fig.29) kryss på ett punkt Å, alltid liggende inne i trekanten Og å være midten av den innskrevne sirkelen(se avsnittet "Innskrevetog omskrevne polygoner").

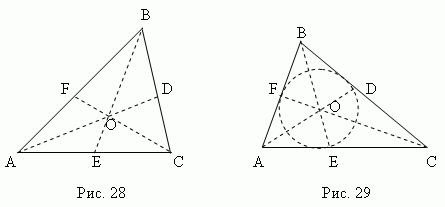
Halveringslinjen deler den motsatte siden i deler proporsjonale med de tilstøtende sidene ; for eksempel i fig. 29 AE: CE = AB: BC.

Median vinkelrett er en vinkelrett trukket fra midten segmentpunkter (sider). Tre vinkelrette halveringslinjer av trekant ABC(KO, MO, NO, Fig. 30 ) skjærer i ett punkt O, som er senter omskrevne sirkel (peker K, M, N – midtpunktene til sidene i trekanten ABC).

I en spiss trekant ligger dette punktet inne i trekanten; i stump - utenfor; i en rektangulær - i midten av hypotenusen. Ortosenter, tyngdepunkt, circumcenter og innskrevet sirkel faller bare sammen i en likesidet trekant.

Pythagoras teorem. I en rettvinklet trekant, kvadratet av lengdeHypotenusen er lik summen av kvadratene av lengdene på bena.

Beviset for Pythagoras teorem følger tydelig av fig. 31. Tenk på en rettvinklet trekant ABC med ben a, b og hypotenusen c.

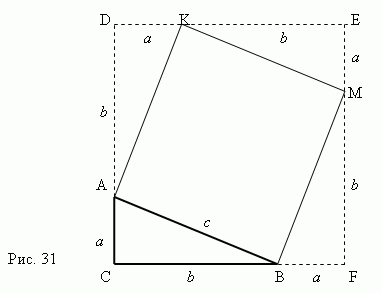
La oss bygge en firkant AKMB ved hjelp av hypotenusen AB som en side. Deretterfortsett sidene i den rette trekanten ABC for å få en firkant CDEF , hvis side er lika + b.Nå er det klart at området på torget CDEF er lik ( a+b) 2 . På den annen side, dette areal er lik summen områder fire rette trekanter og kvadratet AKMB, altså

c 2 + 4 (ab / 2) = c 2 + 2 ab,

herfra,

c 2 + 2 ab= (a+b) 2 ,

og til slutt har vi:

c 2 =en 2 +b 2 .

Aspektforhold i en vilkårlig trekant.

I det generelle tilfellet (for en vilkårlig trekant) har vi:

c 2 =en 2 +b 2 – 2ab· cos C,

hvor C – vinkel mellom sideneen Og b .