Hvordan bestemme tegnet for projeksjonen på en akse. Grunnleggende formler for å finne avstander ved å bruke projeksjon av en vektor på en akse. Vektorprodukt av koordinatenhetsvektorer

§ 3. Projeksjoner av en vektor på koordinataksene

1. Finne projeksjoner geometrisk.

Vektor
- projeksjon av vektoren på aksen OKSE
- projeksjon av vektoren på aksen OY

Definisjon 1. Vektorprojeksjon på en hvilken som helst koordinatakse er et tall tatt med et pluss- eller minustegn, som tilsvarer lengden på segmentet som er plassert mellom basene til perpendikulære slipp fra begynnelsen og slutten av vektoren til koordinataksen.

Projeksjonstegnet er definert som følger. Hvis det, når du beveger deg langs koordinataksen, er en bevegelse fra projeksjonspunktet til begynnelsen av vektoren til projeksjonspunktet til slutten av vektoren i positiv retning av aksen, så anses projeksjonen av vektoren som positiv . Hvis den er motsatt av aksen, anses projeksjonen som negativ.

Figuren viser at hvis vektoren er orientert på en eller annen måte motsatt av koordinataksen, så er projeksjonen på denne aksen negativ. Hvis en vektor på en eller annen måte er orientert i den positive retningen til koordinataksen, så er projeksjonen på denne aksen positiv.

Hvis en vektor er vinkelrett på koordinataksen, er dens projeksjon på denne aksen null.
Hvis en vektor er codirectional med en akse, så er projeksjonen på denne aksen lik den absolutte verdien av vektoren.
Hvis en vektor er rettet motsatt av koordinataksen, er dens projeksjon på denne aksen lik absoluttverdien til den absolutte verdien av vektoren tatt med et minustegn.

2. De fleste generell definisjon projeksjoner.

Fra en rettvinklet trekant ABD: .

Definisjon 2. Vektorprojeksjon på enhver koordinatakse er et tall lik produktet av modulen til vektoren og cosinus til vinkelen som dannes av vektoren med den positive retningen til koordinataksen.

Tegnet på projeksjonen bestemmes av tegnet på cosinus til vinkelen som dannes av vektoren med den positive akseretningen.
Hvis vinkelen er spiss, har cosinus et positivt fortegn og projeksjonene er positive. For stumpe vinkler har cosinus et negativt fortegn, så i slike tilfeller er projeksjonene på aksen negative.
- derfor, for vektorer vinkelrett på aksen, er projeksjonen null.

I fysikk for klasse 9 (IKKikoin, A.K.Kikoin, 1999),
oppgave №5
til kapitlet" KAPITTEL 1. GENERELL INFORMASJON OM TRAFIKK».

1. Hva kalles projeksjonen av en vektor på koordinataksen?

1. Projeksjonen av vektor a på koordinataksen er lengden av segmentet mellom projeksjonene av begynnelsen og slutten av vektor a (perpendikulære slipp fra disse punktene på aksen) på denne koordinataksen.

2. Hvordan er forskyvningsvektoren til et legeme relatert til dets koordinater?

2. Projeksjonene av forskyvningsvektoren s på koordinataksene er lik endringen i de tilsvarende kroppskoordinatene.

3. Hvis koordinaten til et punkt øker over tid, hvilket fortegn har da projeksjonen av forskyvningsvektoren på koordinataksen? Hva om det synker?

3. Hvis koordinaten til et punkt øker over tid, vil projeksjonen av forskyvningsvektoren på koordinataksen være positiv, fordi i dette tilfellet vil vi gå fra projeksjonen av begynnelsen til projeksjonen av slutten av vektoren i retning av selve aksen.

Hvis koordinaten til et punkt avtar over tid, vil projeksjonen av forskyvningsvektoren på koordinataksen være negativ, fordi i dette tilfellet vil vi gå fra projeksjonen av begynnelsen til projeksjonen av slutten av vektoren mot guiden til selve aksen.

4. Hvis forskyvningsvektoren er parallell med X-aksen, hva er da modulen for projeksjonen av vektoren på denne aksen? Og hva med modulen til projeksjonen av den samme vektoren på Y-aksen?

4. Hvis forskyvningsvektoren er parallell med X-aksen, så er modulen til vektorens projeksjon på denne aksen lik modulen til selve vektoren, og dens projeksjon på Y-aksen er null.

5. Bestem fortegnene til projeksjonene på X-aksen til forskyvningsvektorene vist i figur 22. Hvordan endres koordinatene til kroppen under disse forskyvningene?

5. I alle følgende tilfeller endres ikke Y-koordinaten til kroppen, og X-koordinaten til kroppen vil endres som følger:

a) s 1;

projeksjonen av vektoren s 1 på X-aksen er negativ og er lik i absolutt verdi med lengden av vektoren s 1 . Med en slik bevegelse vil X-koordinaten til kroppen minke med lengden på vektoren s 1.

b) s2;

projeksjonen av vektoren s 2 på X-aksen er positiv og lik lengden på vektoren s 1 . Med en slik bevegelse vil X-koordinaten til kroppen øke med lengden på vektoren s 2.

c) s3;

projeksjonen av vektoren s 3 på X-aksen er negativ og lik lengden på vektoren s 3 . Med en slik bevegelse vil X-koordinaten til kroppen minke med lengden på vektoren s 3.

d)s 4;

projeksjonen av vektoren s 4 på X-aksen er positiv og lik lengden på vektoren s 4 . Med en slik bevegelse vil X-koordinaten til kroppen øke med lengden på vektoren s 4.

e) s 5;

projeksjonen av vektoren s 5 på X-aksen er negativ og lik lengden på vektoren s 5 . Med en slik bevegelse vil X-koordinaten til kroppen minke med lengden på vektoren s 5.

6. Hvis verdien av tilbakelagt avstand er stor, kan forskyvningsmodulen da være liten?

6. Kanskje. Dette skyldes at forskyvning (forskyvningsvektor) er en vektormengde, dvs. er et rettet rett linjesegment som forbinder kroppens utgangsposisjon med dens etterfølgende posisjoner. Og den endelige posisjonen til kroppen (uavhengig av tilbakelagt avstand) kan være så nær kroppens utgangsposisjon som ønsket. Hvis den endelige og første posisjonen til kroppen faller sammen, vil forskyvningsmodulen være lik null.

7. Hvorfor er bevegelsesvektoren til en kropp viktigere i mekanikk enn veien den har gått?

7. Mekanikkens hovedoppgave er å bestemme kroppens posisjon til enhver tid. Når vi kjenner kroppens bevegelsesvektor, kan vi bestemme kroppens koordinater, dvs. posisjonen til kroppen til enhver tid, og kun vite avstanden som er tilbakelagt, kan vi ikke bestemme koordinatene til kroppen, fordi vi har ingen informasjon om bevegelsesretningen, men kan bare bedømme lengden på veien som er tilbakelagt på et gitt tidspunkt.

Aksen er retningen. Dette betyr at projeksjon på en akse eller på en rettet linje anses som det samme. Projeksjon kan være algebraisk eller geometrisk. I geometriske termer forstås projeksjonen av en vektor på en akse som en vektor, og i algebraiske termer forstås det som et tall. Det vil si at begrepene projeksjon av en vektor på en akse og numerisk projeksjon av en vektor på en akse brukes.

Hvis vi har en L-akse og en vektor A B → som ikke er null, kan vi konstruere en vektor A 1 B 1 ⇀, som angir projeksjonene til punktene A 1 og B 1.

A 1 B → 1 vil være projeksjonen av vektoren A B → på L.

Definisjon 1

Projeksjon av vektoren på aksen er en vektor hvis begynnelse og slutt er projeksjoner av begynnelsen og slutten av en gitt vektor. n p L A B → → det er vanlig å betegne projeksjonen A B → på L. For å konstruere en projeksjon på L, slippes perpendikulære på L.

Eksempel 1

Et eksempel på en vektorprojeksjon på en akse.

På koordinatplan Omtrent x y er punktet M 1 (x 1 , y 1) spesifisert. Det er nødvendig å konstruere projeksjoner på O x og O y for å avbilde radiusvektoren til punktet M 1. Vi får koordinatene til vektorene (x 1, 0) og (0, y 1).

Hvis vi snakker om projeksjonen av a → på en ikke-null b → eller projeksjonen av a → på retningen b → , så mener vi projeksjonen av a → på aksen som retningen b → sammenfaller med. Projeksjonen av a → på linjen definert av b → er betegnet n p b → a → → . Det er kjent at når vinkelen mellom a → og b → , kan n p b → a → → og b → betraktes som codirectional. I tilfellet hvor vinkelen er stump, er n p b → a → → og b → i motsatte retninger. I en situasjon med perpendikularitet a → og b →, og a → er null, er projeksjonen av a → i retning b → nullvektoren.

Den numeriske egenskapen til projeksjonen av en vektor på en akse er den numeriske projeksjonen av en vektor på en gitt akse.

Definisjon 2

Numerisk projeksjon av vektoren på aksen er et tall som er lik produktet av lengden til en gitt vektor og cosinus til vinkelen mellom den gitte vektoren og vektoren som bestemmer retningen til aksen.

Den numeriske projeksjonen av A B → på L er betegnet n p L A B → , og a → på b → - n p b → a → .

Basert på formelen får vi n p b → a → = a → · cos a → , b → ^ , hvor a → er lengden på vektoren a → , a ⇀ , b → ^ er vinkelen mellom vektorene a → og b → .

Vi får formelen for å beregne den numeriske projeksjonen: n p b → a → = a → · cos a → , b → ^ . Den gjelder for kjente lengder a → og b → og vinkelen mellom dem. Formelen gjelder for kjente koordinater a → og b →, men det finnes en forenklet form.

Eksempel 2

Finn ut den numeriske projeksjonen av a → på en rett linje i retning b → med en lengde a → lik 8 og en vinkel mellom dem på 60 grader. Ved betingelse har vi a ⇀ = 8, a ⇀, b → ^ = 60 °. Så la oss erstatte numeriske verdier inn i formelen n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4 .

Svar: 4.

Med kjent cos (a → , b → ^) = a ⇀ , b → a → · b → , har vi a → , b → som skalarprodukt av a → og b → . Etter formelen n p b → a → = a → · cos a ⇀ , b → ^ , kan vi finne den numeriske projeksjonen a → rettet langs vektoren b → og få n p b → a → = a → , b → b → . Formelen tilsvarer definisjonen gitt i begynnelsen av avsnittet.

Definisjon 3

Den numeriske projeksjonen av vektoren a → på en akse som sammenfaller i retning med b → er forholdet mellom skalarproduktet til vektorene a → og b → og lengden b → . Formelen n p b → a → = a → , b → b → er anvendelig for å finne den numeriske projeksjonen av a → på en linje som sammenfaller i retning med b → , med kjente a → og b → koordinater.

Eksempel 3

Gitt b → = (- 3 , 4) . Finn den numeriske projeksjonen a → = (1, 7) på L.

Løsning

På koordinatplanet har n p b → a → = a → , b → b → formen n p b → a → = a → , b → b → = a x b x + a y b y b x 2 + b y 2 , med a → = (a x , a y ) og b → = b x , b y . For å finne den numeriske projeksjonen av vektoren a → på L-aksen, trenger du: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5.

Svar: 5.

Eksempel 4

Finn projeksjonen av a → på L, sammenfallende med retningen b →, der det er a → = - 2, 3, 1 og b → = (3, - 2, 6). Tredimensjonalt rom er spesifisert.

Løsning

Gitt a → = a x , a y , a z og b → = b x , b y , b z , beregner vi skalarproduktet: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Lengden b → er funnet ved å bruke formelen b → = b x 2 + b y 2 + b z 2 . Det følger at formelen for å bestemme den numeriske projeksjonen a → vil være: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .

Bytt ut de numeriske verdiene: n p L a → = n p b → a → = (- 2) 3 + 3 (- 2) + 1 6 3 2 + (- 2) 2 + 6 2 = - 6 49 = - 6 7 .

Svar: - 6 7.

La oss se på sammenhengen mellom a → på L og lengden på projeksjonen a → på L. La oss tegne en akse L, legge til a → og b → fra et punkt på L, hvoretter vi tegner en vinkelrett linje fra enden a → til L og tegner en projeksjon på L. Det er 5 varianter av bildet:

Først tilfellet med a → = n p b → a → → betyr a → = n p b → a → → , derav n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → a → → .

Sekund tilfellet innebærer bruk av n p b → a → ⇀ = a → · cos a → , b → , som betyr n p b → a → = a → · cos (a → , b →) ^ = n p b → a → → .

Tredje tilfellet forklarer at når n p b → a → → = 0 → får vi n p b ⇀ a → = a → · cos (a → , b → ^) = a → · cos 90 ° = 0 , deretter n p b → a → → = 0 og n p b → a → = 0 = n p b → a → → .

Fjerde saken viser n p b → a → → = a → · cos (180 ° - a → , b → ^) = - a → · cos (a → , b → ^) , følger n p b → a → = a → · cos ( a → , b → ^) = - n p b → a → → .

Femte tilfellet viser a → = n p b → a → → , som betyr a → = n p b → a → → , derfor har vi n p b → a → = a → · cos a → , b → ^ = a → · cos 180° = - a → = - n p b → a → .

Definisjon 4

Den numeriske projeksjonen av vektoren a → på L-aksen, som er rettet på samme måte som b →, har følgende verdi:

lengden på projeksjonen av vektoren a → på L, forutsatt at vinkelen mellom a → og b → er mindre enn 90 grader eller lik 0: n p b → a → = n p b → a → → med betingelsen 0 ≤ (a → , b →) ^< 90 ° ;
null forutsatt at a → og b → er vinkelrette: n p b → a → = 0, når (a → , b → ^) = 90 °;
lengden av projeksjonen a → på L, multiplisert med -1, når det er en stump eller rett vinkel av vektorene a → og b →: n p b → a → = - n p b → a → → med betingelsen 90 °< a → , b → ^ ≤ 180 ° .

Eksempel 5

Gitt lengden på projeksjonen a → på L, lik 2. Finn den numeriske projeksjonen a → forutsatt at vinkelen er 5 π 6 radianer.

Løsning

Fra betingelsen er det klart at denne vinkelen er stump: π 2< 5 π 6 < π . Тогда можем найти числовую проекцию a → на L: n p L a → = - n p L a → → = - 2 .

Svar: - 2.

Eksempel 6

Gitt et plan O x y z med en vektorlengde a → lik 6 3, b → (- 2, 1, 2) med en vinkel på 30 grader. Finn koordinatene til projeksjonen a → på L-aksen.

Løsning

Først beregner vi den numeriske projeksjonen av vektoren a →: n p L a → = n p b → a → = a → · cos (a → , b →) ^ = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .

Etter betingelse er vinkelen spiss, da er den numeriske projeksjonen a → = lengden på projeksjonen av vektoren a →: n p L a → = n p L a → → = 9. Denne saken viser at vektorene n p L a → → og b → er samrettet, noe som betyr at det er et tall t som likheten er sann for: n p La → → = t · b → . Herfra ser vi at n p L a → → = t · b → , som betyr at vi kan finne verdien av parameteren t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .

Deretter n p La → → = 3 · b → med koordinatene til projeksjonen av vektor a → på L-aksen lik b → = (- 2 , 1 , 2), hvor det er nødvendig å multiplisere verdiene med 3. Vi har n p L a → → = (- 6 , 3 , 6) . Svar: (- 6, 3, 6).

Det er nødvendig å gjenta den tidligere lærte informasjonen om tilstanden for kollinearitet til vektorer.

Hvis du oppdager en feil i teksten, merk den og trykk Ctrl+Enter

Algebraisk projeksjon av en vektor på enhver akse er lik produktet av lengden til vektoren og cosinus til vinkelen mellom aksen og vektoren:

Pr a b = |b|cos(a,b) eller

Der a b er skalarproduktet av vektorer, |a| - modul til vektor a.

Bruksanvisning. For å finne projeksjonen av vektoren Pr a b online, må du spesifisere koordinatene til vektorene a og b. I dette tilfellet kan vektoren spesifiseres på planet (to koordinater) og i rommet (tre koordinater). Den resulterende løsningen lagres i en Word-fil. Hvis vektorer er spesifisert gjennom koordinatene til punktene, må du bruke denne kalkulatoren.

Klassifisering av vektorprojeksjoner

Typer projeksjoner per definisjon vektorprojeksjon

Den geometriske projeksjonen av vektoren AB på aksen (vektor) kalles vektoren A"B", hvor begynnelsen A' er projeksjonen av begynnelsen A på aksen (vektoren), og slutten B' er projeksjonen. av enden B på samme akse.
Den algebraiske projeksjonen av vektoren AB på aksen (vektoren) kalles lengden av vektoren A"B", tatt med et + eller -tegn, avhengig av om vektoren A"B" har samme retning som aksen ( vektor).

Typer projeksjoner i henhold til koordinatsystemet

Vektorprojeksjonsegenskaper

Den geometriske projeksjonen av en vektor er en vektor (har en retning).
Den algebraiske projeksjonen av en vektor er et tall.

Vektorprojeksjonsteoremer

Teorem 1. Projeksjonen av summen av vektorer på en hvilken som helst akse er lik projeksjonen av summene av vektorene på samme akse.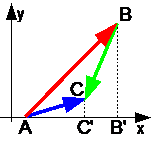

AC" =AB" +B"C"

Teorem 2. Den algebraiske projeksjonen av en vektor på en hvilken som helst akse er lik produktet av lengden på vektoren og cosinus til vinkelen mellom aksen og vektoren:

Pr a b = |b|·cos(a,b)

Typer vektorprojeksjoner

projeksjon på OX-aksen.
projeksjon på OY-aksen.
projeksjon på en vektor.

Projeksjon på OX-aksen	Projeksjon på OY-aksen	Projeksjon til vektor
Hvis retningen til vektor A'B' faller sammen med retningen til OX-aksen, har projeksjonen av vektor A'B' et positivt fortegn.	Hvis retningen til vektoren A'B' faller sammen med retningen til OY-aksen, har projeksjonen av vektoren A'B' et positivt fortegn.	Hvis retningen til vektor A'B' faller sammen med retningen til vektor NM, så har projeksjonen av vektor A'B' et positivt fortegn.
Hvis retningen til vektoren er motsatt av retningen til OX-aksen, har projeksjonen av vektoren A'B' et negativt fortegn.	Hvis retningen til vektor A'B' er motsatt av retningen til OY-aksen, har projeksjonen av vektor A'B' et negativt fortegn.	Hvis retningen til vektor A'B' er motsatt av retningen til vektor NM, så har projeksjonen av vektor A'B' et negativt fortegn.
Hvis vektor AB er parallell med OX-aksen, er projeksjonen av vektor A’B’ lik den absolutte verdien av vektor AB.	Hvis vektor AB er parallell med OY-aksen, er projeksjonen av vektor A’B’ lik den absolutte verdien av vektor AB.	Hvis vektor AB er parallell med vektor NM, er projeksjonen av vektor A’B’ lik den absolutte verdien av vektor AB.
Hvis vektoren AB er vinkelrett på aksen OX, så er projeksjonen A’B’ lik null (nullvektor).	Hvis vektoren AB er vinkelrett på OY-aksen, er projeksjonen A’B’ lik null (nullvektor).	Hvis vektoren AB er vinkelrett på vektoren NM, så er projeksjonen A’B’ lik null (nullvektor).

1. Spørsmål: Kan projeksjonen av en vektor ha negativt fortegn? Svar: Ja, projeksjonsvektoren kan være en negativ verdi. I dette tilfellet har vektoren motsatt retning (se hvordan OX-aksen og AB-vektoren er rettet)
2. Spørsmål: Kan projeksjonen av en vektor falle sammen med den absolutte verdien av vektoren? Svar: Ja, det kan det. I dette tilfellet er vektorene parallelle (eller ligger på samme linje).
3. Spørsmål: Kan projeksjonen av en vektor være lik null (nullvektor). Svar: Ja, det kan det. I dette tilfellet er vektoren vinkelrett på den tilsvarende aksen (vektor).

Eksempel 1. Vektoren (fig. 1) danner en vinkel på 60° med OX-aksen (den er spesifisert av vektor a). Hvis OE er en skalaenhet, så |b|=4, altså .

Faktisk, lengden på vektoren ( geometrisk projeksjon b) er lik 2, og retningen faller sammen med retningen til OX-aksen.

Eksempel 2. Vektoren (fig. 2) danner en vinkel (a,b) = 120 o med OX-aksen (med vektor a). Lengde |b| vektor b er lik 4, så pr a b=4·cos120 o = -2.

Faktisk er lengden på vektoren 2, og retningen er motsatt av retningen til aksen.

Projeksjon vektor på en akse er en vektor som oppnås ved å multiplisere skalarprojeksjonen til en vektor på denne aksen og enhetsvektoren til denne aksen. For eksempel, hvis en x – skalarprojeksjon vektor EN til X-aksen, deretter en x Jeg- dens vektorprojeksjon på denne aksen.

La oss betegne vektorprojeksjon det samme som selve vektoren, men med indeksen til aksen som vektoren er projisert på. Så vektorprojeksjonen til vektoren EN på X-aksen betegner vi EN x ( fett en bokstav som angir en vektor og et underskrift av aksenavnet) eller (en ikke-fet skrift som angir en vektor, men med en pil øverst (!) og en underskrift av aksenavnet).

Skalarprojeksjon vektor per akse kalles Antall, hvis absolutte verdi er lik lengden på aksesegmentet (på den valgte skalaen) innelukket mellom projeksjonene av startpunktet og endepunktet til vektoren. Vanligvis i stedet for uttrykket skalarprojeksjon de sier bare - projeksjon. Projeksjonen er merket med samme bokstav som den projiserte vektoren (i normal, ikke-fet skrift), med en lavere indeks (som regel) av navnet på aksen som denne vektoren er projisert på. For eksempel hvis en vektor projiseres på X-aksen EN, da er projeksjonen angitt med en x. Når den samme vektoren projiseres på en annen akse, hvis aksen er Y, vil dens projeksjon bli betegnet som en y.

For å beregne projeksjonen vektor på en akse (for eksempel X-aksen), er det nødvendig å trekke koordinaten til startpunktet fra koordinaten til endepunktet, dvs.
a x = x k − x n.
Projeksjonen av en vektor på en akse er et tall. Dessuten kan projeksjonen være positiv hvis verdien x k er større enn verdien x n,

negativ hvis verdien x k er mindre enn verdien x n

og lik null hvis x k er lik x n.

Projeksjonen av en vektor på en akse kan også bli funnet ved å kjenne modulen til vektoren og vinkelen den lager med denne aksen.

Fra figuren er det klart at a x = a Cos α

det vil si at projeksjonen av vektoren på aksen er lik produktet av modulen til vektoren og cosinus til vinkelen mellom retningen til aksen og vektor retning. Hvis vinkelen er spiss, da
Cos α > 0 og a x > 0, og, hvis stump, så er cosinus til den stumpe vinkelen negativ, og projeksjonen av vektoren på aksen vil også være negativ.

Vinkler målt fra aksen mot klokken anses som positive, og vinkler målt langs aksen er negative. Men siden cosinus er en jevn funksjon, det vil si Cos α = Cos (− α), kan vinkler telles både med klokken og mot klokken ved beregning av projeksjoner.

For å finne projeksjonen av en vektor på en akse, må modulen til denne vektoren multipliseres med cosinus til vinkelen mellom retningen til aksen og retningen til vektoren.

Vektorkoordinater— koeffisienter for den eneste mulige lineære kombinasjonen av basisvektorer i det valgte koordinatsystemet, lik den gitte vektoren.

hvor er koordinatene til vektoren.

Skalært produkt vektorer

Skalært produkt av vektorer[- i endelig dimensjonal vektorrom er definert som summen av produktene av identiske komponenter som multipliseres vektorer.

For eksempel, S.p.v. en = (en 1 , ..., en n) Og b = (b 1 , ..., b n):

(en , b ) = en 1 b 1 + en 2 b 2 + ... + a n b n