Praktisk leksjon "beregning av derivater". Praktisk leksjon "beregne deriverte" Finn den deriverte av funksjonen y
Leksjonens mål:
Pedagogisk- kjenne differensieringsformler; differensieringsregler;
differensiering av en kompleks funksjon; fysisk og geometrisk betydning av derivat;
likning av tangenten til grafen til en funksjon.
Utviklingsmessig - kunne finne deriverte av funksjoner; løse problemer ved hjelp av fysisk betydning, geometrisk betydning; finn verdien av den deriverte av en funksjon i et punkt; matematisk korrekt forklare og begrunne handlingene som er utført.
Pedagogisk – dyrke selvstendighet, ansvar, refleksjon.
I løpet av timene
I. Organisatorisk øyeblikk.
II. Sjekker lekser
(i pauser sjekker konsulenter (studenter) og setter karakterer).
III. Målsetting og motivasjon
Læreren informerer elevene om at denne leksjonen er den siste leksjonen om emnet "Beregne derivater" og inviterer dem til å formulere sine egne mål.
Lærer: "Den store filosofen Confucius sa en gang: "Tre veier fører til kunnskap: Refleksjonsveien er den edleste veien, etterligningens vei er den enkleste veien, og erfaringens vei er den bitreste veien." Så i dag i klassen vil hver av dere bestemme hvilken vei til kunnskap om dette emnet han er på.»
Studentene får i oppgave å demonstrere sine kunnskaper og ferdigheter i å beregne derivater og får en leksjonsplan.
Trinn I: Fullføre oppgaven ved å bruke "Husk"-kortet.
(teste kunnskap om formler og differensieringsregler).
Trinn II: Muntlig frontarbeid om repetisjon og generalisering av kunnskap.
Trinn III:"Testprognose" (når du utfører denne oppgaven, er hjelp fra konsulenter akseptabelt).
JegTrinn V: Løsning av et praktisk problem.
Trinn V: Selvstendig arbeid
Trinn I, III, V av arbeid og lekser vurderes. Konsulenter sjekker og legger inn resultatene i evalueringstabellen.
Evalueringskriterier: "5"- 19-20 poeng;
"4"- 15-18 poeng;
"3"- 10-14 poeng.
Veier til kunnskap
- Reproduksjon og korrigering av referansekunnskap
Trinn I.
Mål: kontroll, selvkontroll av kunnskap om formler og regler for differensiering
Huske! F.I. ________________________________________________ |
|
Derivat |
|
c,c - ulemper t |
|
|
|
|
|
f"(x)+ g"(x) |
|
f(x)* g(x) |
|
|
|
På slutten av denne oppgaven utføres en selvtest ved å bruke "Table of Derivatives". Kort overleveres konsulenter for verifisering (rettelser på kort er ikke tillatt).
V. Generalisering og systematisering av kunnskap
Trinn II.
1. Muntlig frontalt arbeid.
EN. Generer en oppgave for denne tilstanden og løs den.
![]()
1. Finn verdien av den deriverte av funksjonen i punktet t = 3. (Svar: 21.)
2. Lag en ligning for tangenten til grafen til funksjonen i punktet t = 3. (Svar: y = 21x-45.).
3. Finn kroppens hastighet og akselerasjon i øyeblikket t=3c, hvis bevegelsesloven er gitt av formelen. (Svar: 21 m/s, 16 m/s²).
4. Finn vinkelkoeffisienten til tangenten trukket til grafen til funksjonen i punktet t = 3. (Svar: 21.).
5. Finn tangenten til hellingsvinkelen til tangenten til grafen til funksjonen i punktet t = 3 og bestem vinkeltypen mellom tangenten og den positive retningen til Ox-aksen. (Svar: tgα, vinkel α er spiss)
B. Finn deriverte av funksjoner

2. Trinn III«Testprognose»


På slutten av denne oppgaven utføres en selvtest basert på de endelige svarene og testene overleveres til konsulenter. (rettelser på kort er ikke tillatt).
Svar:
1 alternativ |
||||
Alternativ 2 |
- Løsningen på problemet
JegTrinn V
Frontal løsning på et avansert nivå problem (løsningen utføres av konsulenter sammen med klassen).
Oppgave
Ved hvilke parameterverdier en tangenter til grafen til en funksjon ![]()
tegnet ved skjæringspunktene med X-aksen, danner en vinkel på 60° mellom seg?

Grafen er en parabel med oppadgående grener som skjærer X-aksen i to punkter (tilfellet en=0 tilfredsstiller ikke meningen med problemet):
IX. Oppsummering og karaktersetting
1. Spørsmål: a) Er hensikten med leksjonen nådd?
b) Hvilket stadium virket vanskeligst?
c) Hva var mest interessant?
2. Konsulenter kunngjør resultatene (antall og navn på studenter på vei
imitasjon, måter å reflektere på og måter å oppleve).
Praktisk jobb
matematikk
1. Finne grensen for en funksjon. Den første og andre er fantastiske grenser.
2. Derivert av en kompleks funksjon. Studie av en funksjon av én variabel og plotte grafer.
3. Test "Anvendelse av differensialregning til studiet av funksjoner."
4. Finne ubestemte integraler. Beregning av bestemte integraler.
5. Beregning av determinanter.
6. Løse systemer av lineære ligninger ved hjelp av Cramer-metoden. Test.
7. Løse problemer om emnet "Set". Logiske algebraformler.
8. Beregning av sannsynligheter for tilfeldige hendelser. Total sannsynlighetsformel.
9. Beregning av numeriske egenskaper.
10. Test "Grunnleggende for sannsynlighetsteori og matematisk statistikk"
11. Trigonometrisk form av et komplekst tall.
12. Handlinger med komplekse tall i ulike former.
METODOLOGISK INSTRUKSJON FOR PRAKTISK ARBEID I MATEMATIKK
KURS 2
En praktisk leksjon er en form for organisering av utdanningsprosessen, som innebærer at elever utfører ett eller flere praktiske arbeider på oppdrag og under veiledning av en lærer.
I praktiske timer i matematikk utvikler elevene således evnen til å løse problemer, som i fremtiden bør brukes til å løse faglige problemer i spesielle disipliner.
I løpet av praktisk arbeid behersker studentene evnen til å bruke informasjonskilder, arbeide med forskriftsdokumenter og undervisningsmateriell, oppslagsverk, lage tegninger, diagrammer, tabeller, løse ulike typer oppgaver og gjøre beregninger.
Oppgaver som løses i praktiske timer i matematikk:
1) utvidelse og konsolidering av teoretisk kunnskap i matematikk tilegnet under forelesninger;
2) utvikle i studentene de praktiske ferdighetene og evnene som er nødvendige for å lykkes med å løse problemer i matematikk;
3) utvikling av elevenes behov for egenutdanning og forbedring av kunnskap og ferdigheter i prosessen med å studere matematikk;
4) dannelse av en kreativ holdning og forskningstilnærming i prosessen med å studere matematikk;
5) dannelse av faglig betydningsfulle egenskaper hos en fremtidig spesialist og ferdigheter i å anvende ervervet kunnskap i det profesjonelle feltet.
Praktisk leksjon nr. 1. Beregning av funksjonsgrenser. Den første og andre er fantastiske grenser.
Emne : Beregning av funksjonsgrenser.
Mål: tilegnelse av grunnleggende kunnskap innen grunnleggende grener av matematikk . Testing av assimilering av kunnskap om beregning av grenser for funksjoner. Gjenta og systematisere kunnskap om dette emnet.
Oppgaver:
Utvikling av kreativ faglig tenkning;
Mestring av vitenskapens språk, ferdigheter til operasjonskonsepter;
Mestre ferdighetene til å sette og løse problemer;
Utdype teoretisk og praktisk opplæring;
Utvikling av initiativ og selvstendighet hos studentene.
Styrke dataferdigheter;
Fortsett å jobbe med matematisk tale.
Dannelse av ferdigheter for selvstendig arbeid, arbeid med en lærebok, ferdigheter for selvstendig å tilegne seg kunnskap;
Utvikling av evnen til å fremheve det viktigste når du arbeider med tekst;
Dannelse av uavhengig tenkning, mentale operasjoner: sammenligning, analyse, syntese, generalisering, analogi;
Vis elevene rollen til systematisk arbeid for å utdype og øke kunnskapsstyrken, på kulturen for å fullføre oppgaver;
Utvikling av elevenes kreative evner.
Gir praktisk arbeid:
Teoretisk materiale med metodiske anbefalinger for praktisk arbeid.
Matematikk, – Serie: Yrkesfaglig videregående opplæring. - Rostov-ved-Don "Phoenix", s.
Fremdrift av den praktiske leksjonen.
1.Formulering av emnet for leksjonen, forklaring av sammenhengen mellom emnet og andre emner i den akademiske disiplinen;
2. Sjekke elevenes beredskap for timen;
3. Gjennomføring av den faktiske leksjonen i henhold til emnet og i samsvar med arbeidsprogrammet for faget:
Studer teoretisk materiale om emnet "Beregne grensene for funksjoner."
Tenk på eksempler på å løse typiske oppgaver.
Gjør selvstendig arbeid med å beregne grensene for funksjoner ved å bruke den første og andre bemerkelsesverdige grensen.
Svar på sikkerhetsspørsmål.
Teoretisk informasjon og metodiske anbefalinger
på problemløsning.
1. Presentasjon av teoretisk stoff.
For å beregne grensen for en funksjon på et punkt, må du:
1) Erstatt i stedet for variabelen x det x har en tendens til.
2) Hvis vi etter å ha fullført trinn 1) får en usikkerhet på skjemaet https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">og erstatte pilen med minus: (x-a).
3) Hvis vi, etter å ha fullført trinn 1), mottar en usikkerhet på skjemaet https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> assosiert med verdiene til trigonometriske funksjoner, må vi bruke den første bemerkelsesverdige grensen.
Definisjon. Den første bemerkelsesverdige grensen kalles grensen
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Definisjon:Den andre bemerkelsesverdige grensen kalt grense

Tallet gitt av denne grensen spiller en svært viktig rolle både i matematisk analyse og i andre grener av matematikken. Nummeret ringes opp base av naturlige logaritmer ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Konsolidering av det studerte materialet.
Eksempel 1
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Vi brukte regel 1) og erstattet i stedet for x det x skal strebe etter, dvs. x=2.
Eksempel 2
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
Eksempel 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6
Eksempel 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" height="30 src=">
Eksempel 5
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
Eksempel 6
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
b) 
V) 
3. Konsolidering av kunnskap, ferdigheter og evner.
Gjør selvstendig arbeid med å beregne grensene for funksjoner.
Praktisk arbeid nr. 1. valg 1 Regn ut grensen for funksjonen: 1. 2. 3. 10. | Praktisk arbeid nr. 1. Alternativ 2 Regn ut grensen for funksjonen: 1. 2. 3. 10. |
Praktisk arbeid nr. 2.
Emne : Finne den deriverte av en funksjon. Studie av en funksjon av en variabel og plotte en graf.
Mål : Teste i praksis kunnskap om begrepet en derivert av en funksjon, evnen til å finne deriverte av elementære funksjoner, komplekse funksjoner, inverse funksjoner, ved hjelp av tabellen med deriverte og differensieringsregler, begrepet en kompleks og invers funksjon, evnen å bruke en derivert for å studere funksjoner.
Gir praktisk arbeid:
Lærebok. "Matematikk". – M.: Bustard, 2010.
Matematikk. M: Forum-Infa 2008.
Individuelle kort med praktisk arbeidsmulighet.
1. Teoretisk materiale og eksempler på å finne den deriverte av en funksjon.
Definisjon: Den deriverte av funksjonen f(x) (f"(x)) i punkt x er grensen for forholdet mellom økningen av funksjonen og økningen av argumentet når økningen av argumentet har en tendens til null:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
Regler for differensiering.
Hvis funksjonene f(x) og g(x) har deriverte, da
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, hvor C=konst
5..png" width="49" height="54 src=">
6. Derivat av en kompleks funksjon:
f′(g(x))=f′(g) g′(x)
2. Eksempler.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).
Funksjonen er produktet av to faktorer: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
Funksjonen er kvotienten av to uttrykk: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " height="57 src=">.png" width="197 height=36" height="36">
Løsning. La oss finne den deriverte av denne funksjonen ved å bruke regelen for differensiering av komplekse funksjoner (formel 6):

5. Hvis , da 
6. y = x 3 – 3x 2 + 5x+ 2. La oss finne y "(–1).
y " = 3x 2 – 6x+ 5. Derfor, y "(–1) = 14.
7. Hvis y= logg x cos x, Det y" = (ln x)"cos x+ln x(cos x) " =1/x∙cos x–ln x synd x.
La en funksjon gis. For å studere det trenger du:
1) Finn dets definisjonsdomene. Hvis det ikke er for vanskelig, er det nyttig å finne utvalget også. (I mange tilfeller blir imidlertid spørsmålet om funn utsatt til ytterpunktene av funksjonen er funnet.)
2) Finn ut de generelle egenskapene til funksjonen som vil hjelpe til med å bestemme dens oppførsel: om funksjonen er partall eller oddetall, om den er periodisk.
3) Finn ut hvordan funksjonen oppfører seg når argumentet nærmer seg grensepunktene til definisjonsdomenet, hvis det finnes slike grensepunkter. Hvis en funksjon har diskontinuitetspunkter, bør disse punktene også kontrolleres for tilstedeværelsen av vertikale asymptoter for funksjonen. Finn skrå asymptoter.
4) Finn skjæringspunktene til grafen med koordinataksene, som består av ganske enkelt å beregne verdien av funksjonen under betingelsen:
Med OX-akse: y=0;
Med OY-akse: x=0.
Å finne skjæringspunktene med aksen kan føre til behovet for å løse en kompleks algebraisk ligning, som kanskje bare kan gjøres omtrentlig. Etter å ha funnet røttene til funksjonen og diskontinuitetspunktene, kan vi bestemme fortegnet til funksjonen i hvert av intervallene mellom disse punktene. Dette kan gjøres enten ved å beregne verdien av funksjonen når som helst i intervallet, eller ved å bruke intervallmetoden.
5) Finn intervaller for monotonitet. For å gjøre dette, finn den deriverte og løs ulikheten:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, funksjonen minker.
Etter å ha funnet intervallene for monotonisitet, kan vi umiddelbart bestemme punktene for lokalt ekstremum: der en økning erstattes av en reduksjon, er lokale maksima lokalisert, og hvor en reduksjon erstattes av en økning, er lokale minima lokalisert.
6) Å finne intervallene for konveksitet og konkavitet utføres ved å bruke den andre deriverte..png" width="39" height="19 src="> på intervallene:
hvis https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, så er funksjonsgrafkurven konveks.
Samtidig definerer vi bøyningspunkter som de punktene der funksjonen endrer konveksitetsretningen (og er kontinuerlig).
7) Finne skjæringspunktene til grafen med asymptoten og tilleggspunkter. Dette punktet er ikke obligatorisk, men å finne slike punkter gjør studiet av funksjonen og dens graf komplett og komplett.
Merk at det er nyttig å umiddelbart plotte punktene på koordinataksene og på grafen som oppnås under studiet av funksjoner på tegningen. Dette bidrar til å forstå grafens utseende underveis.
3. Gjør det selv:
|
alternativ | Finn den deriverte av funksjonen y: |
alternativ | Finn den deriverte av funksjonen y: |
1.y=6- | 1. y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Praktisk leksjon
Emne: Finne derivater. Anvendelse av den deriverte til studiet av funksjoner og plotting av grafer.
Mål: Mestre beregningen av deriverte, lær å utforske en funksjon ved å bruke den deriverte
Utdanningsmidler: notatbøker for praktiske øvelser, presentasjoner om emnet, Internett-ressurser.
1. Vurder teoretisk materiale om emnene: "Regler for beregning av derivater", "Ekstremum av en funksjon", "Konveksitet, konkavitet. Bøyningspunkt."
2. Gjennomgå prøver av oppgaver.
3. Fullfør testoppgave nr. 1.
Kontrollspørsmål:
1. Definer maksimum (minimum) for en funksjon i et punkt. Hva kan sies om tegnet på økningen av funksjonen i et ganske lite nabolag med maksimum (minimum) punktet?
2. Hva er de nødvendige betingelsene for eksistensen av et ekstremum av en funksjon? Hva er deres geometriske betydning?
3. Hva er regelen for å finne de største og minste verdiene til en funksjon på et segment?
4. Definer konveksitet (konkavitet) til en kurve på et intervall.
5. Hva er regelen for å finne intervallene for konveksitet og konkavitet for en kurve?
6. Kurvens bøyningspunkt. Hvordan finne henne?
7. Hva er algoritmen for å konstruere en graf for en funksjon?
Regler for beregning av derivater
Derivat av en kompleks funksjon.
Hvis på=ƒ( Og), u=φ(x), da på¢ ( X)=ƒ¢ (i)·φ¢ (X).
Avledet av en sum.
Hvis på(X)=Og(X)+v (X), Det på¢ (X)=Og¢ (X)+v ¢ (X)
Derivat av produktet.
Hvis y(x)=u(X)· v (X), Det på¢ = Og¢ · v + u · v ¢ .
Spesielt, ( Med· Og)¢ =c· Og¢, det vil si at konstantfaktoren tas ut fra under det deriverte tegnet. Det er lett å verifisere det
(u 2 ) ¢ = 2 u·u ¢ , (u 3 ) ¢ =3u 2 u ¢ , … , (u n ) ¢ =n·u n–1 u ¢ .
Avledet av kvotienten.
Hvis da  .
.
Derivattabell
1. (Med)¢ =0
For en kompleks funksjon: if u=u(x), Det:
2. (X)¢ =1
3. (X α )¢ = α · Xα–1, EN– et hvilket som helst reelt tall.
 .
.
3. 
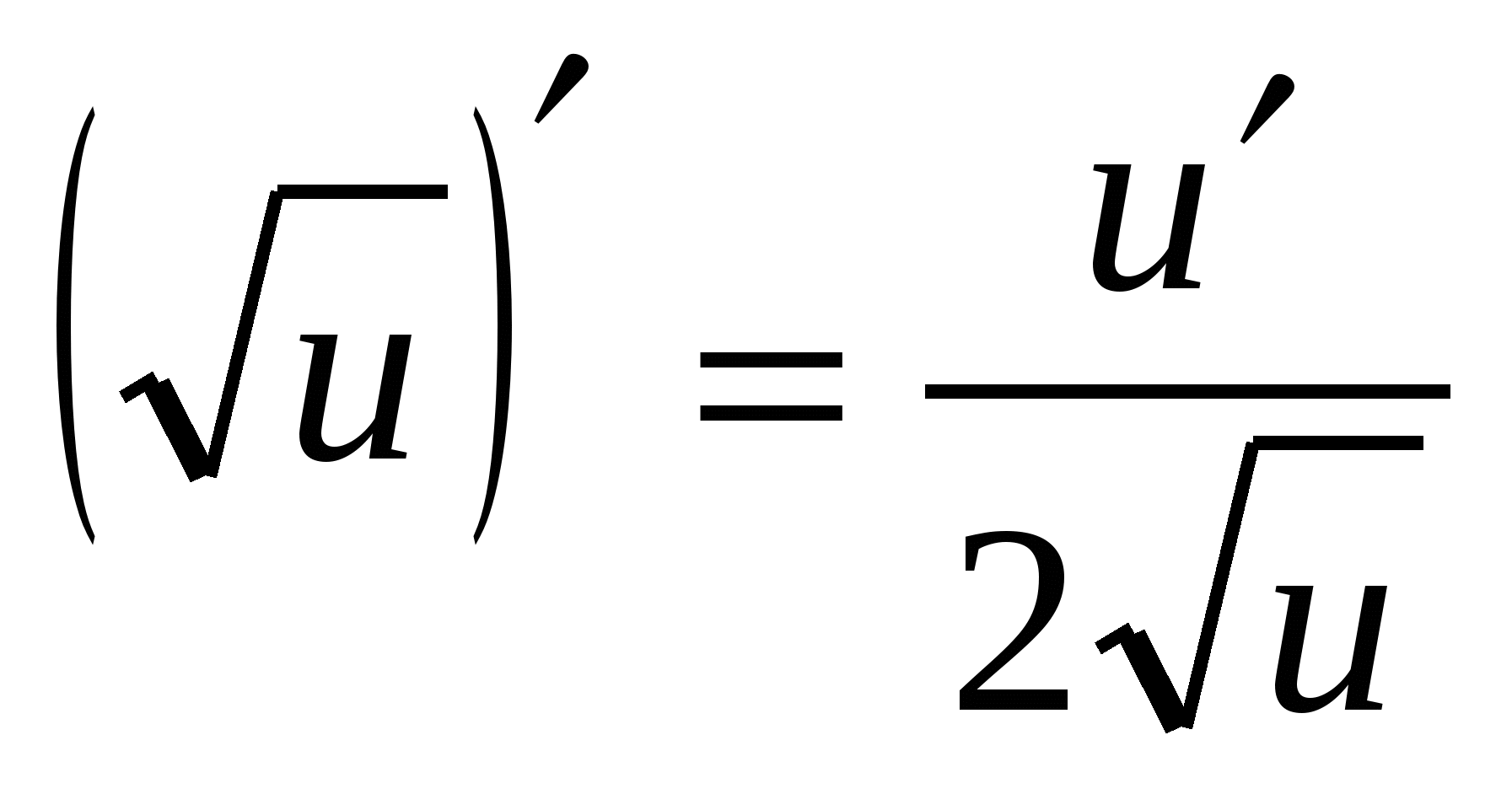
4. (EN X ) ¢ =a X · ln EN
4. 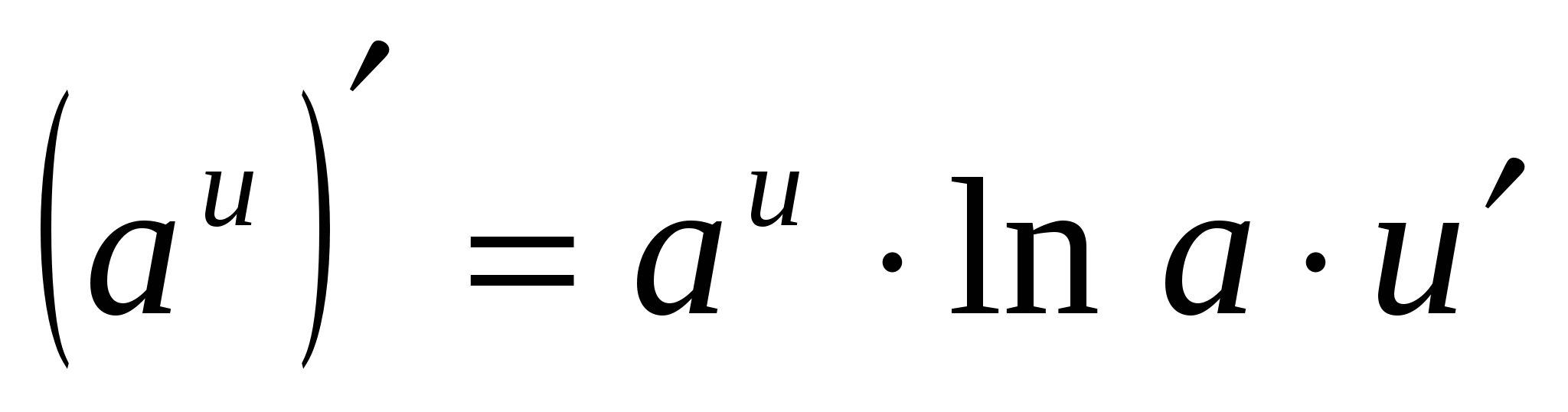
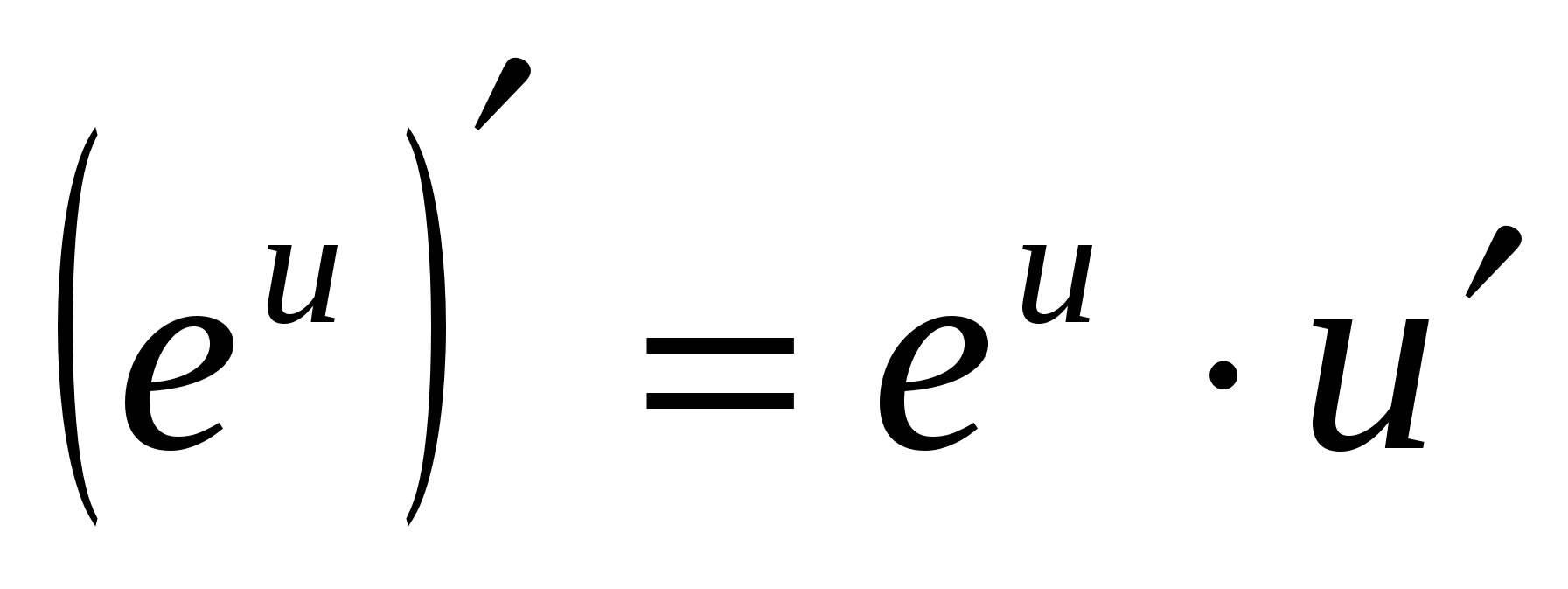
5. (Logg
en
x)
¢
=
 .
.
5. 

6. (synd x)¢ =cos x
6. 
7. (cos x)¢ = –sin x
7. 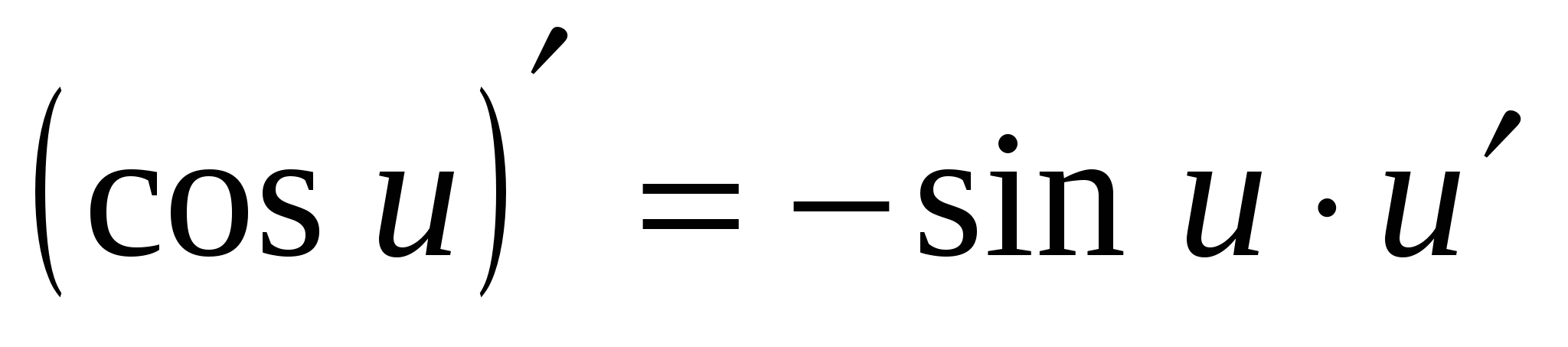
8. (tg x)¢
=
8. 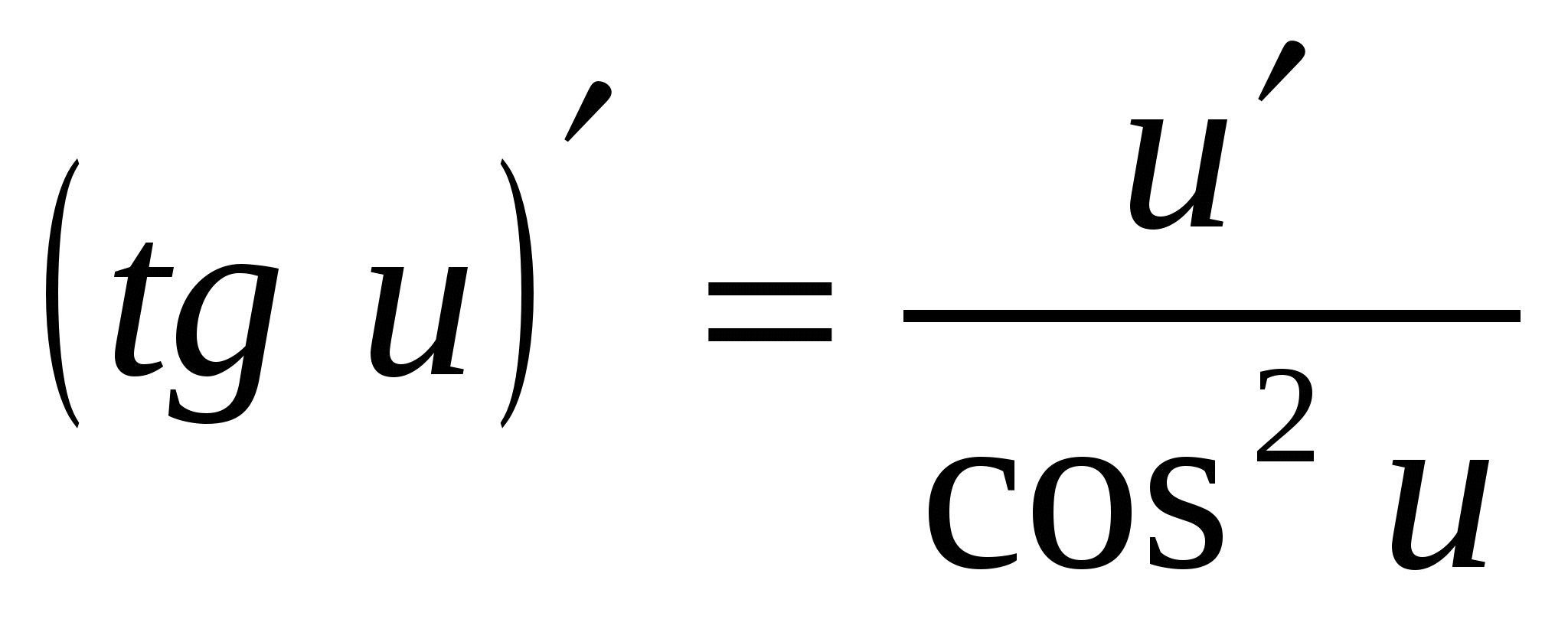
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 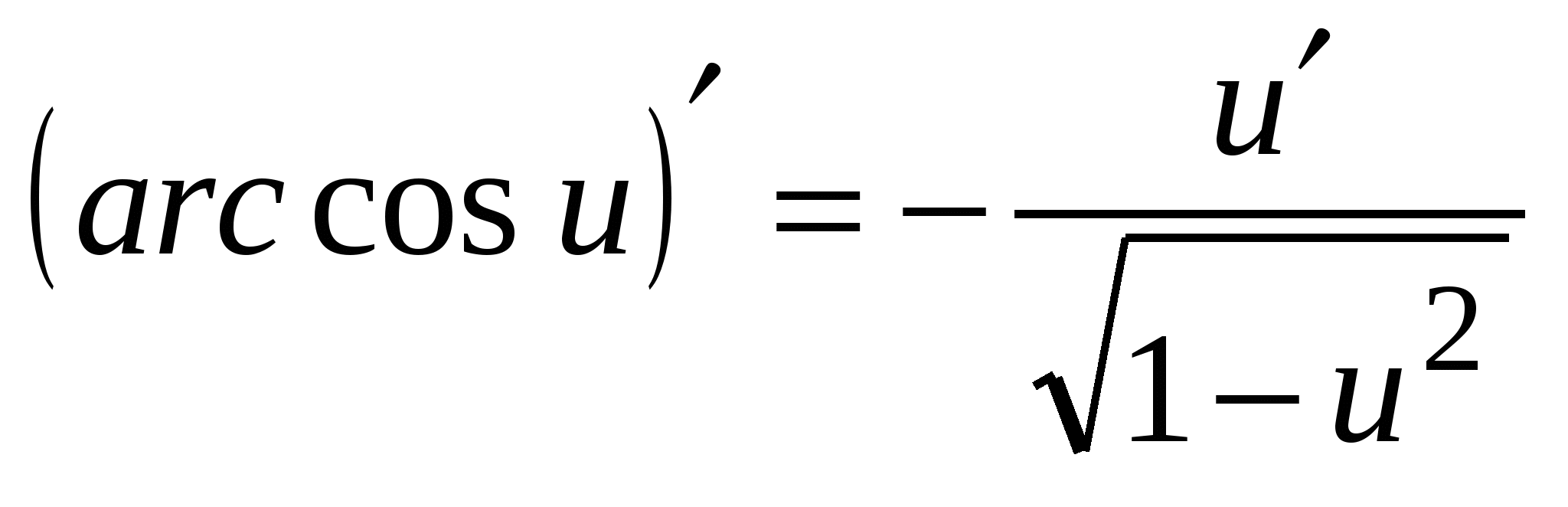
12. 
12. 
13. 
13. 
Gjennomgå eksempler
Eksempel 1.
y=(3–2 synd 5x ) 4 | Vi bruker derivatformler for Og α ,synd u |
y ¢ =4·(3–2·sin5x) 3·(3–2sin5x) ¢ =4·(3–2·sin5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
Eksempel 2.
. 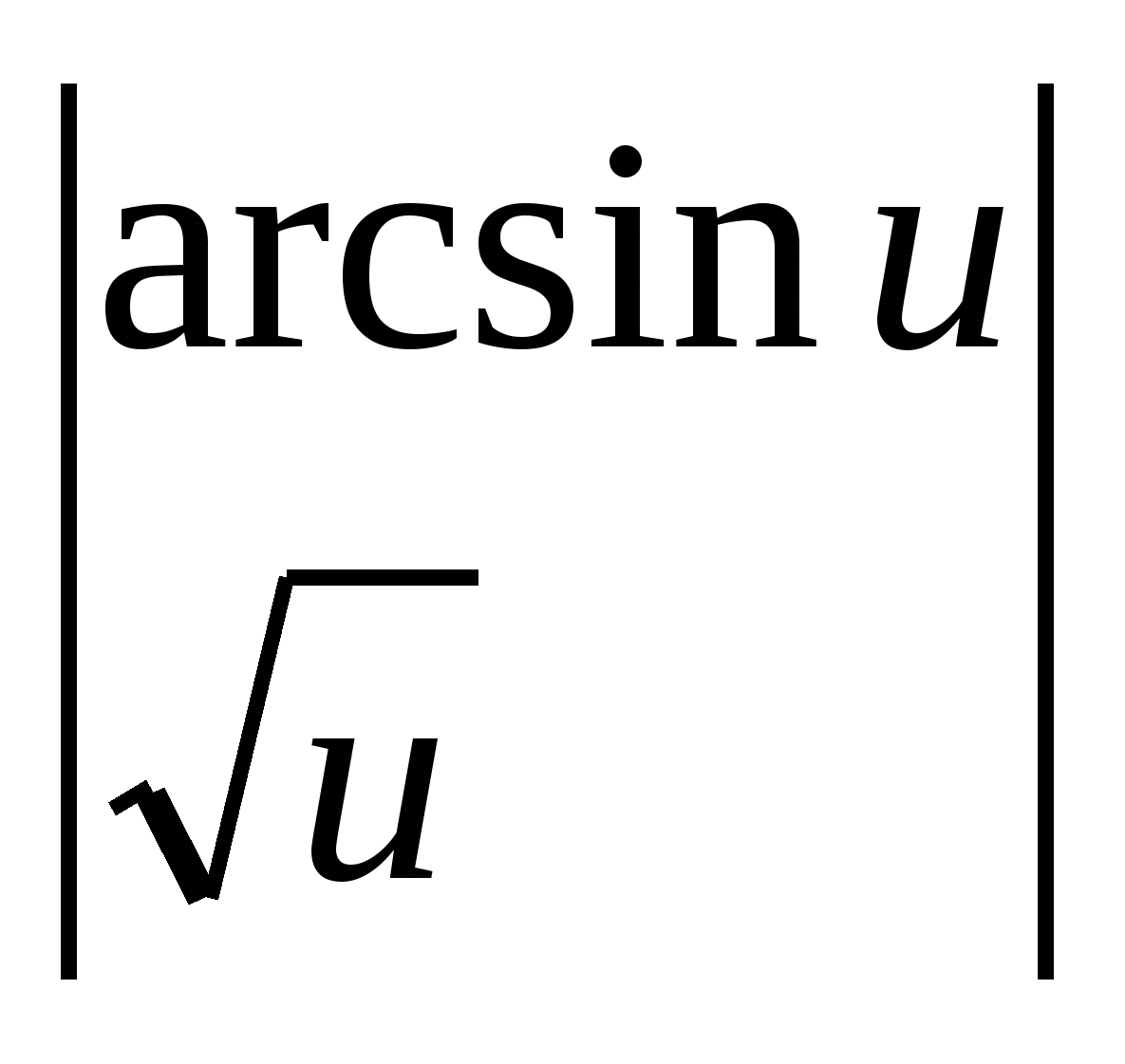

Eksempel 3.
 .
. 

Eksempel 4.



Eksempel 5.
 .
. 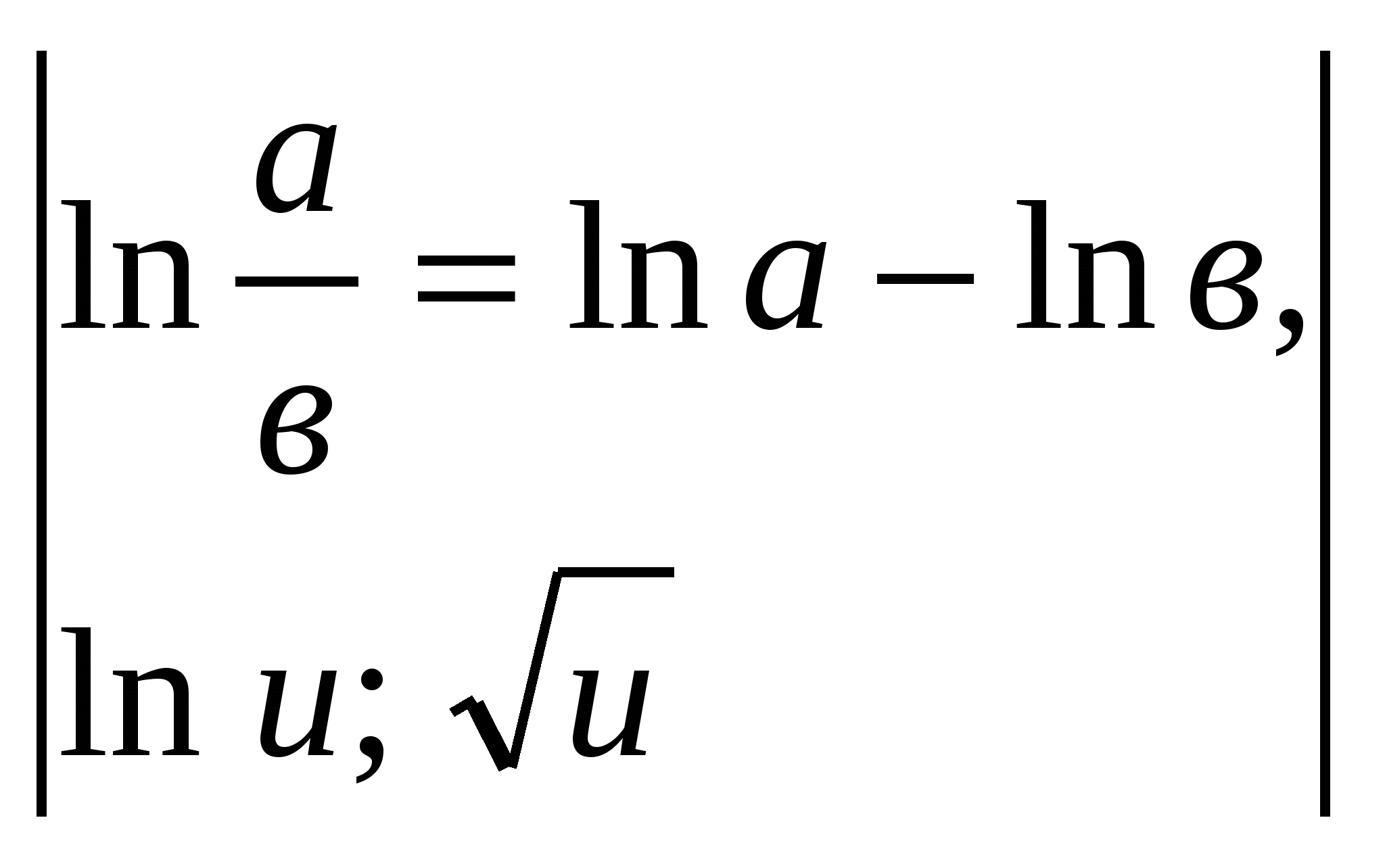

Extremum av funksjonen
Studiet av en funksjon ved et ekstremum er en av de viktigste anvendelsene av derivater. La oss se på definisjonen av minima og maksima, og hvordan du finner dem.
La funksjonen ƒ( X) er definert og differensierbar på et bestemt sett og et punkt X 0 er et punkt inne i den.
Definisjon. Funksjon ƒ (X) på punktet X 0 har maksimum(minimum), hvis det er et slikt nabolag av punktet X 0, som er for alle X fra dette området ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Punktum X 0 kalles da et punkt maksimum(minimum).

Ris. 1.
Det vises en graf for en funksjon som har to maksimumspunkter ( X 1 og X 3) og to minimumspoeng ( X 2 og X 4), og maksimumsverdien kan være mindre enn minimum ( ƒ (X 1 ) < ƒ (X 4)). Dette understreker det faktum at vi karakteriserer singulariteten til en funksjon bare nær et bestemt punkt.
Verdiene til funksjonen ved punktene maksimum og minimum kalles ekstreme verdier eller ytterpunkter. Grafen ovenfor viser at ekstremumpunktene ( X 1 , X 2 , X 3 , X 4) bestemme intervallene for monotonisitet av funksjonen, i hver av dem beholder derivatet et visst tegn. Ved ekstreme punkter går selvfølgelig den deriverte til null. La oss formulere et teorem om nødvendig tilstand eksistensen av et ekstremum.
Teorem. Hvis funksjonen ƒ (X) på punktet X 0 har et ekstremum, så er den deriverte av funksjonen på dette punktet lik null, dvs. ƒ¢ ( X 0)=0.
La oss umiddelbart merke seg at denne betingelsen ikke er tilstrekkelig, det vil si at det motsatte utsagnet ikke alltid er sant. Fra likestilling ƒ ¢ ( X 0)= 0 betyr ikke nødvendigvis det på punktet X 0 det er et ekstremum.
Dette bekreftes av et eksempel med funksjonen ƒ (X)=x 3 .
Vi finner ƒ ¢ ( X)= 3X 2 . På punktet X=0 ƒ ¢ (0)=0 . Men så nærme poenget du vil X=0 finner vi X> 0, hvor ƒ (X)=x 3 > 0, vi finner X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, hvor for alle X funksjonsverdi i et punkt X=0 vil være størst eller minste. Derfor peker X=0 er ikke et ekstremumpunkt.
Man kan argumentere annerledes. Siden derivatet ƒ ¢ (x)=3x 2 , deretter funksjonen ƒ(x)=x 3 øker for enhver reell x og har ingen ekstreme.
Punkter der den nødvendige ekstreme betingelsen er oppfylt (ƒ ¢ (x)=0) er kalt kritisk .
Tydeligvis er tangenten til grafen til funksjonen i punktene der ƒ ¢ (x)=0, parallelt med x-aksen Ox .
Tilstrekkelig tilstand ekstremum er gitt i følgende teoremer.
Teorem 1. Hvis X 0 er det kritiske punktet for funksjonen, og når den passerer gjennom den, endrer den deriverte fortegn X 0 er et ekstremumpunkt, nemlig hvis den deriverte endrer fortegn fra pluss til minus, er det et maksimumspunkt, og hvis den endrer fortegn fra minus til pluss, er det et minimumspunkt.
Merk at det ikke er noe ekstremum på et punkt hvis den deriverte ikke endrer fortegn. Regelen for å studere ekstremum ved bruk av førstederiverte er kjent fra skolekurset. Noen ganger er det mer praktisk å formulere en tilstrekkelig betingelse for et ekstremum ved å bruke den andre deriverte.
La funksjonen ƒ( X) er to ganger differensierbar i noen domene (dvs. ƒ( X) har ƒ¢ ( X) Og ƒ ¢¢ ( X)).
Teorem 2. Hvis X 0 – kritisk punkt for funksjonen ƒ(x) og ƒ ¢¢ (X 0 ) > 0 , Det X 0 – minimumspoeng, hvis ƒ ¢¢ (X 0 ) < 0, то X 0 – maksimum poeng.
Ved å bruke den andre deriverte bestemmes konveksiteten eller konkaviteten til grafen til en funksjon.
Konveksitet, konkavitet. Bøyningspunkt.
Kurve y=ƒ(X) er kalt konvekstth under noen av henne tangent
ƒ ¢¢ ( X) < 0.
Kurve y=ƒ(X) er kalt konkav på et intervall hvis alle punktene i kurven ligger høyere noen av henne tangent på dette intervallet. Så på dette intervallet
ƒ ¢¢(x) > 0
Definisjon. Bøyningspunkt en kurve er et punkt hvor kurven er konveks på den ene siden og konkav på den andre.
Ved bøyningspunktet ƒ ¢¢ ( X)=0.
Så tegnet til den andre deriverte (så vel som tegnet til selve funksjonen og dens første deriverte) indikerer egenskapene til funksjonsgrafen. La oss se på dem igjen.
Hvis for alle X på intervallet ( EN, b) ƒ (X) > 0 (ƒ (X) < 0), så ligger grafen over (under) x-aksen.
Hvis for alle X på intervallet ( EN, b) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (EN, b) øker (minker).
Hvis for alle X på intervallet ( EN, b) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (EN, b) konkav (konveks).
Ligning ƒ( X)=0 definerer "nullene" til funksjonen, dvs. skjæringspunktene til grafen med okseaksen.
Ligningen ƒ ¢ ( X)=0 definerer kritiske punkter.
Ligningen ƒ ¢¢ ( X)=0 definerer mulige bøyningspunkter.
Funksjonsstudieordning
For å studere funksjonen ƒ (X) og plotting y=ƒ(X) bør finnes:
1) definisjonsdomenet til funksjonen og skjæringspunktet til grafen med koordinataksene;
2) intervaller av monotoni;
3) ekstreme punkter og funksjonsverdier på disse punktene;
4) intervaller for konveksitet og konkavitet av grafen;
5) bøyningspunkter for grafen;
6) konstruer i et kartesisk koordinatsystem alle de oppnådde punktene (noen ganger, for å tydeliggjøre grafen, oppnås ytterligere punkter) og selve grafen.
De minste og største verdiene til en funksjon på et segment
Når du løser noen problemer med optimaliseringsmetoden, er det viktig å kunne finne de minste eller største verdiene av en funksjon på et bestemt segment. Funksjonen når disse verdiene enten på kritiske punkter eller i enden av segmentet.
Søkeopplegg de minste og største verdiene for funksjonen ƒ (X) på segmentet [ EN, b].
1. Finn den deriverte av funksjonen ƒ ¢ ( X).
2. Finn de kritiske punktene fra ligningen ƒ ¢ ( X)=0.
3. Velg de kritiske punktene som tilhører dette segmentet [ EN, b] og finn verdien av funksjonen ƒ (X) på hvert slikt punkt.
4. Beregn funksjonsverdier ƒ (X) på slutten av segmentet: ƒ( EN) og ƒ( b).
5. Velg den største (største) og minste (minste) fra de oppnådde funksjonsverdiene.
Eksempel 2.
Finn de største og minste verdiene til en funksjon ƒ(x)=X 3 –9x 2 +24х–10 på segmentet.
1. ƒ ¢ ( X)= 3X 2 – 9·2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. Punkt x 2 =4 hører ikke til segmentet. Derfor beregner vi verdien av funksjonen kun ved punktet X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Funksjonsverdier ved enden av segmentet: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Oppnådde verdier:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Den høyeste verdien er 10 og nås ved punktet X=2. Den minste er lik –10 og oppnås ved punktet X=0.
Eksempel 3.
Finn intervallene for konveksitet og konkavitet og bøyningspunkter for kurven y=x+36X 2 –2X 3 –X 4 .
Definisjonsdomenet til denne funksjonen er settet av alle reelle tall, dvs. XЄ(–∞, +∞).
La oss finne den andre deriverte.
på¢ =1+72 X–6X 2 –4X 3 .
p墢 =72–12 X–12X 2 = –12(X 2 +X–6).
Fra Eq. p墢 =0 får vi abscissen til bøyningspunktet:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
La oss definere tegnet p墢 på intervaller
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
p墢
kurveform
konveks
bøyning
konkav
bøyning
konveks
La oss finne ordinatene til bøyningspunktene:
på(–3)=726; M 1 (–3; 726) – bøyningspunkt
på(2)=114; M 2 (2; 114) – bøyningspunkt.
På intervallet (–3; 2) er kurven konkav. På intervallene (–∞; –3) og (2; +∞) – konveks.
Eksempler på oppgaver
Oppgave nr. 1.
Finn bruddpunktene til funksjonen og plott grafen

Funksjon ƒ (X) er definert for alle ekte X og er kontinuerlig på hvert av de angitte intervallene: (–∞; –1), [–1; 0], (0, +∞). La oss utforske funksjonen ƒ (X) for kontinuitet på punkter X= –1 og X=0.
For å gjøre dette vil vi finne ensidige grenser på hvert av disse punktene.

Siden de ensidige grensene er forskjellige, altså X = –1 – diskontinuitetspunkt av den første typen.
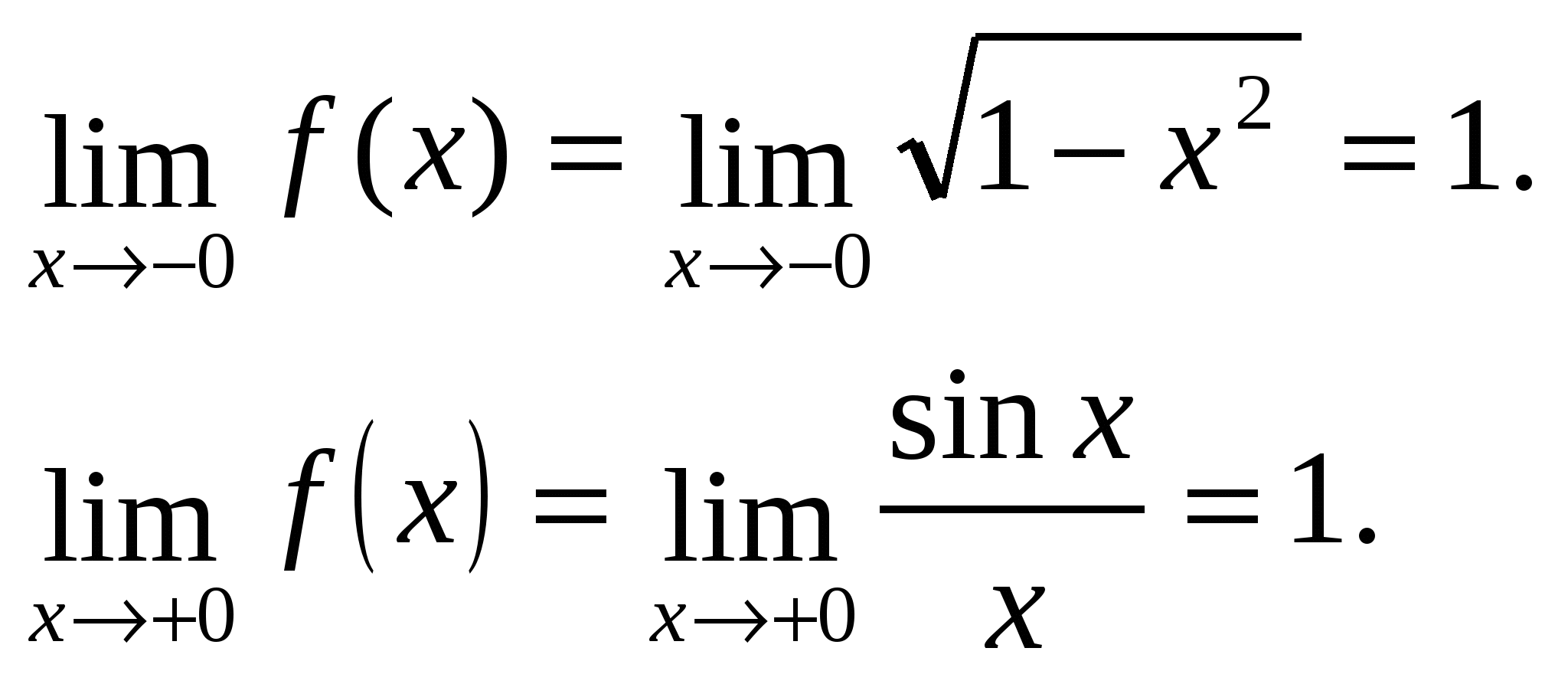
Ensidige grenser er like, dvs. ved punktet x=0 er det en grense for funksjonen og 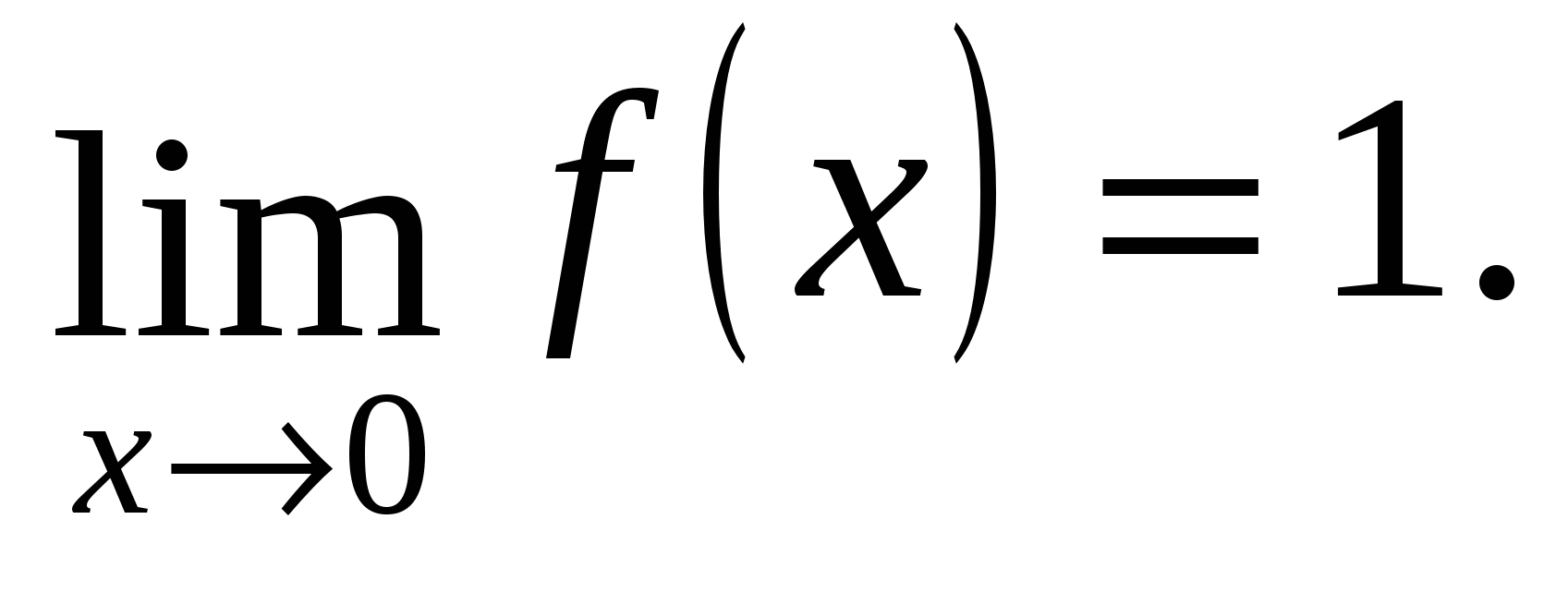
La oss sammenligne denne grensen med verdien av funksjonen på punktet: 
Fordi  så inn ved x=0 er funksjonen ƒ(x) kontinuerlig.
så inn ved x=0 er funksjonen ƒ(x) kontinuerlig.
La oss plotte funksjonen ƒ (X), gitt at
1)  – ligning av en rett linje,
– ligning av en rett linje,
2)  – ligningen til den øvre halvsirkelen
– ligningen til den øvre halvsirkelen  med sentrum ved origo og radius lik enhet, og under betingelsen –1 £ X£ 0 ligning
med sentrum ved origo og radius lik enhet, og under betingelsen –1 £ X£ 0 ligning  definerer en kvartsirkel.
definerer en kvartsirkel.
3) for X > 0 grafen er gitt av ligningen  . Vi finner skjæringspunktene til denne kurven med okseaksen fra ligningen
. Vi finner skjæringspunktene til denne kurven med okseaksen fra ligningen 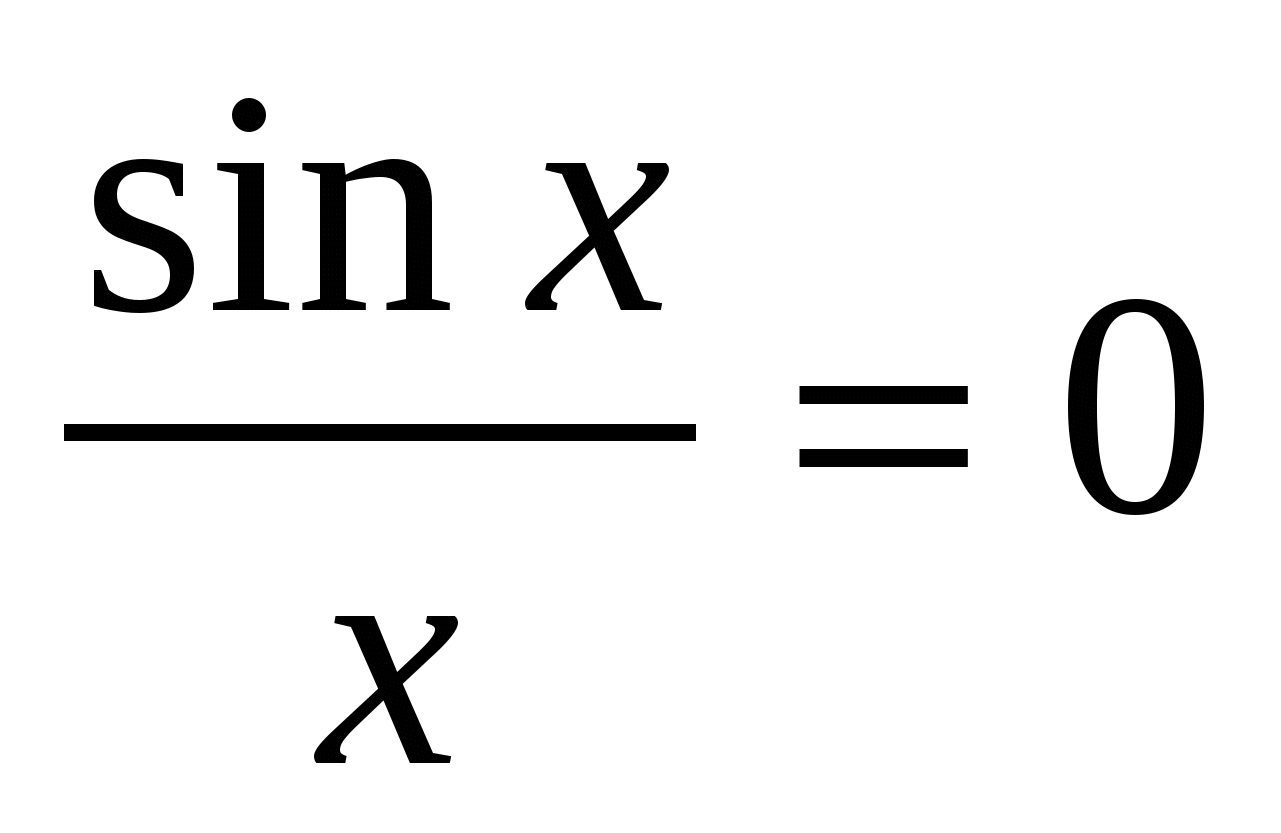 for x > 0. x= π
n, Hvor n
=1, 2, 3, 4,
for x > 0. x= π
n, Hvor n
=1, 2, 3, 4,

Ris. 2.
Oppgave nr. 2.
Skriv likninger for tangenter til en linje  på punkter hvor X=0 og X=4. Finn skjæringspunktet mellom tangentene og vinkelen mellom dem. Lag en tegning.
på punkter hvor X=0 og X=4. Finn skjæringspunktet mellom tangentene og vinkelen mellom dem. Lag en tegning.
Ligning av en tangent til en linje y=ƒ(x) ser ut som
Hvor på 0 =ƒ( X 0).
På punktet X=0 på(0)=ƒ(0)=5.
på¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
M 1 (0, 5) har formen y– 5= –3(X–0) eller
y= –3X+5.
På punktet X=4 på(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Ligning av en tangent i et punkt M 2 (4, 1) har formen y– 1=X–4 eller
y=x–3.
Vi får skjæringspunktet til tangentene ved å løse systemet

Krysspunkt M 3 (2, –1).
Hjørne φ mellom tangenter finner vi fra formelen:
 ,
,
Hvor k 1 = –3; k 2 =1 – vinkelkoeffisienter for tangenter.
 .
.
Hjørne φ =arctg 2.
La oss bygge denne linjen  – en parabel med et toppunkt på punktet hvor X=3, fordi på¢
=0 kl X=3. Vi finner
– en parabel med et toppunkt på punktet hvor X=3, fordi på¢
=0 kl X=3. Vi finner  . Punktum M 4 (3;
. Punktum M 4 (3;  ) er toppunktet til parablen.
) er toppunktet til parablen.
R 
er. 3.
Oppgave nr. 3.
Utforsk funksjon 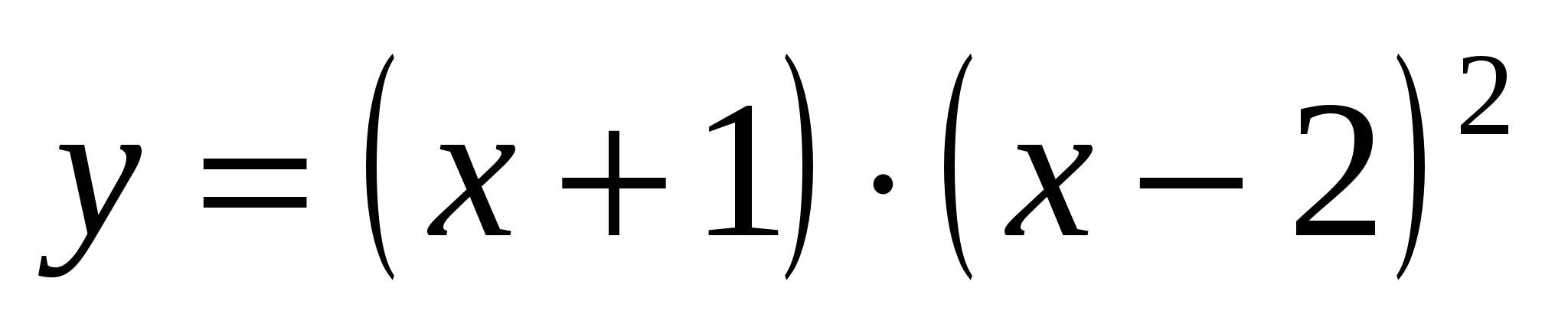 og plotte det.
og plotte det.
1. Denne funksjonen er et polynom (du kan åpne parentesene, vi får et polynom av tredje grad), derfor er den definert, kontinuerlig og differensierbar for evt. X.
2. La oss finne den deriverte.
 .
.
Fra Eq. på¢ =0 la oss finne kritiske punkter: 3 X·( X–2)=0, X 1 =0, X 2 =2.
La oss utforske dem.
X
(–∞, 0)
(0; 2)
(2; +∞)
på ¢
på
3. Så, funksjonen øker på intervallene (–∞, 0) og (2, +∞), reduseres på intervallet (0; 2), har et maksimum ved x=0 og et minimum ved x=2:
på maks = på(0)=4; på min = på(2)=0.
4. La oss finne den andrederiverte.
p墢 = 6·( X-1).
Kurven er konveks hvor p墢 < 0, т. е. 6·(X–1) < 0, X < 1.
Kurven er konkav hvor p墢 > 0, dvs. X > 1.
Så på intervallet (–∞, 1) er kurven konveks; og på intervallet (1, +∞) er den konkav.
5. Vi finner bøyningspunktet fra ligningen p墢 =0. Dermed, X=1 – abscisse av bøyningspunktet, fordi dette punktet skiller intervallene for konveksitet og konkavitet til kurven. Bøypunktsordinat: på(1)=2.
Graf av en funksjon på=(X+1)·( X–2) 2 skjærer Ox-aksen ved på=0, dvs. når X= –1 og X=2;
krysser Oy-aksen kl X=0, dvs. når på=4. Vi fikk tre poeng: (–1; 0), (2; 0), (0; 4). Vi vil legge inn alle de oppnådde poengene i tabellen, og legge til de ved siden av dem.
–2
–1



–16


er. 4 Kurve y=(x+1)(x–2) 2.
Oppgave nr. 1
Vi presenterer deg for oppgaver som kan ha ett, to, tre eller flere riktige svar. Sett ring rundt tallene for alle riktige svar.
1. Hvis  deretter funksjonen
deretter funksjonen
1) økende
2) avtagende
3) konstant
2. Hvis
1) Økende
2) Avtagende
3. Hvis  , deretter funksjonen
, deretter funksjonen
1) Økende
2) Avtagende
4. Hvis  , deretter funksjonen
, deretter funksjonen
1) Økende 3) Avtagende
2) Konstant 4) Monoton
5. Funksjon  Er
Er
1) Til og med
2) Ikke engang
3) verken partall eller oddetall
4) Periodisk
5) Ikke periodisk
6) Trigonometrisk
7) Elementær
6. Funksjon  Er
Er
1) til og med
2) merkelig
3) verken partall eller oddetall
4) periodisk
5) ikke periodisk
6) trigonometrisk
7) elementært
2) Weierstrass 4) Dirichlet 6) Leibniz
8) Løsning  Ligninger
Ligninger
1) 0 3) 0 og 3 5) 2 7) 3
2) 2 og 3 4) 2 6) -5 og 1 8) 5 og 1
9) løsning på ulikhet 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 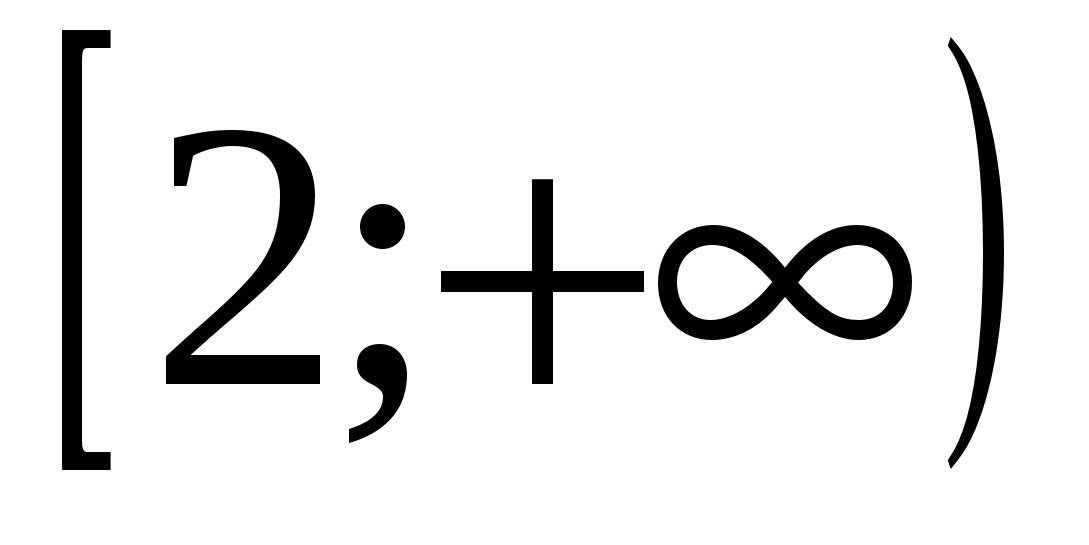
10) Metode  Mengden er funnet
Mengden er funnet
1) vektorer
2) rett
3) segment
11) Hvis  , deretter funksjonen
, deretter funksjonen
1) Konkav 3) Konveks 5) Avtagende
2) Monotonisk 4) Økende 6) Konstant
12) definisjonsdomenet til funksjonen er lik 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 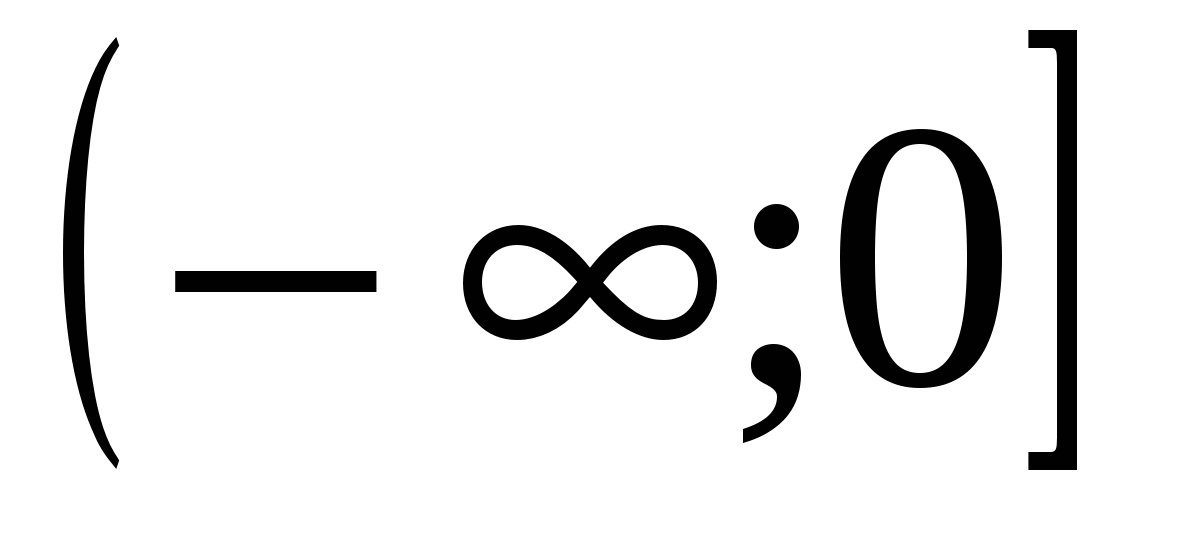
7) (-1;1)
8) 
9) 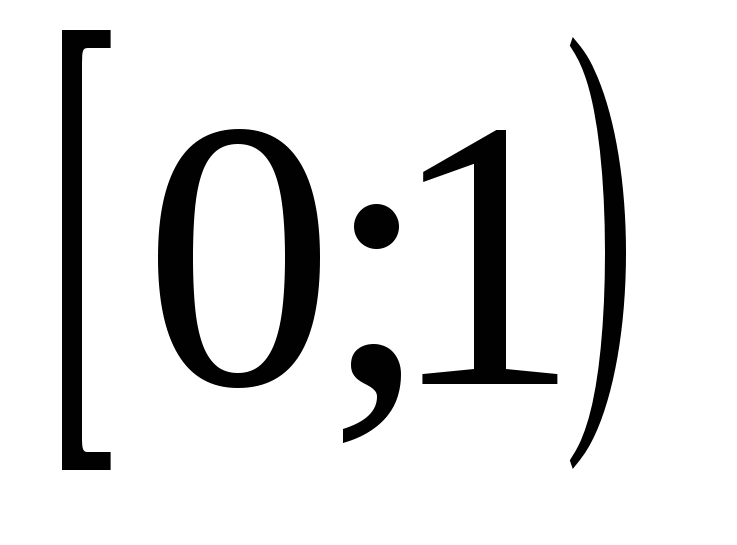
13) funksjon  er
er
1) veiledende
2) trigonometrisk
3) kraft
4) logaritmisk
14) hvis funksjonene y = x  da er hun det
da er hun det 
1) til og med
2) merkelig
3) verken partall eller oddetall
15) funksjon  på
på  er
er

 .
.


