Tester for konvergens av upassende integraler. Hvordan beregne et upassende integral og finne ut dets konvergens. Definisjon og grunnleggende egenskaper
Teorem 12.11 (test for sammenligning av upassende integraler). La funksjonene f(x) og g(x) være kontinuerlige på intervallet [a, ">) og tilfredsstille betingelsen 0 fix) ?(x) på den. Så fra konvergensen av integralet
integralet konvergerer
og omvendt, fra divergensen til integralet (12.64) følger divergensen til integralet (12.63).
Bevis. La oss introdusere følgende notasjon:
Funksjon P(K) er ikke-minkende; faktisk hvis og jeg 2, da
J fastsette) dx>0, og deretter
La oss ta en sekvens av verdier (/?„) -> “>; deretter den tilsvarende sekvensen av funksjonsverdier (F(Rn)) er monotont og ikke-avtagende. La integralet (12.63) konvergere, deretter sekvensen (67 ( R it)) er begrenset; men da er også rekkefølgen begrenset (F(/?„)), som betyr at ved setning 7.13 konvergerer den. Derfor er det en grense F(R) på R-+ «>, dvs. integral (12,64) konvergerer.
La oss nå bevise den andre delen av teoremet; la integral (12,64) divergere. Hvis vi antar at integralet (12.63) konvergerer, så bør integralet (12.64) etter det som ble bevist ovenfor også konvergere, noe som motsier betingelsen. Teoremet er bevist. ?
Kommentar. Et lignende sammenligningskriterium er også gyldig for upassende integraler av den andre typen. Hvis funksjonene /(x) og g (X) kontinuerlig på halvintervall [a>b) og for alle punkter i et eller annet nabolag til entallspunktet b fullført
forhold 0 (x), så følger det fra konvergensen av integralet Jg(x)dx
divergensen til integralet J/(x)dx, og fra divergensen til integralet J/(x)dx -
potensen til integralet Jg(x)dx.
La oss vurdere eksempler for å studere konvergensen av upassende integraler.
Eksempel 27. T. ^-.
X 3 (1 + e L)
Løsning. La oss sammenligne integranden i dette integralet med funksjonen
Dg. Det er åpenbart at -r-
X g* (1+0 x J
gral J-jdx konvergerer; derfor, i kraft av sammenligningskriteriet, den gitte 1 X
siste integral.
Eksempel 28. I-.
Løsning. Ved å sammenligne integranden til dette integralet med funksjonen 1/x,
vi ser at (1 + In x)/x > 1/x på intervall 1
diversifiserer, derfor divergerer dette integralet til sammenligning også.
Avslutningsvis presenterer vi uten bevis Cauchy-kriteriet for konvergens av et upassende integral av den første typen.
12.10.4. Absolutt og betinget konvergens av upassende integraler
Definisjon 5. Et upassende integral J/(x)dx kalles absolutt
konvergent, hvis integralet J|/(x)|dx konvergerer.
Definisjon 6. Det upassende integralet J /(x) dx kalles betinget lik
varig, hvis den konvergerer og integralet J|/(x)|dx divergerer.
Merk at den absolutte konvergensen til integralet innebærer dets konvergens på grunn av estimat 3 bestemt integral og Cauchy-kriteriet.
Teorem 12.13 (Dirichlet-Abel test*). La funksjonen /(x) være kontinuerlig og ha en avgrenset antideriverte F(x) på intervallet [a, «>], og funksjonen g(x) har en kontinuerlig derivert på dette intervallet, øker ikke og har en tendens til null som x -> ©o. Deretter den upassende integralen
konvergerer.
Bevis. La oss bruke integrering av deler til integralet J /(x)g(x)dx
på et vilkårlig segment R R" Med [ EN, °°). Vi har:
Teorem 12.12. For at det upassende integralet (12.64) skal konvergere, er det nødvendig og tilstrekkelig at man for enhver e > 0 kan finne et slikt tall EN> 0, som for evt R" og /?", større enn EN, ulikhet gjelder:
I henhold til betingelsene for teoremet F(x) begrenset, dvs. |F(x)| K. Funksjonen g(x) øker ikke og har en tendens til null som x -” ">, som betyr. g(x)> 0, a g"(x)
Abel Niels Henrik (1802-1829) - norsk matematiker.
Siden, i henhold til betingelsene for teoremet, g(x) -» 0 for x -> ©°, for et vilkårlig tall e > 0 kan vi finne tallet A> slik at når R"> L ulikheten vil bli tilfredsstilt g(R") Ved å erstatte dette med estimat (12.68), får vi:

som tilsvarer Cauchy-kriteriet for konvergens av integralet (12.66). Teoremet er bevist. ?
La oss vurdere eksempler på bruk av Dirichlet-Abel-testen for konvergens av upassende integraler.
Eksempel 29. f^^dx, a>0.
Løsning. La oss sette /(x) = sin x, g(x)= l/x"; det er lett å verifisere at alle betingelsene i teoremet er oppfylt, det vil si at dette integralet konvergerer. For a > 1 er dette integralet
ral konvergerer absolutt. Faktisk, |synd x/xP 1/d L, integral J(l/x e)dx
konvergerer, dvs. Ved sammenligningskriteriet (Setning 12.11) konvergerer også dette integralet absolutt.
Eksempel 30. Jsin x 2 dx - Fresnel-integral, o
Løsning. La oss representere dette integralet som en sum:
Siden synd x 2 - kontinuerlig funksjon på intervallet (0, 1J, det første integralet i (12.69) eksisterer. For å bestemme konvergensen til det upassende integralet på høyre side av (12.69), setter vi /(x) = x sin x 2, g(x) = 1/x. Deretter for funksjonen /(x) antideriverten F(x) = -cosx 2 /! er avgrenset på intervallet |1, ">), og #(x) er positiv, har en tendens til null som x -" °° og har en kontinuerlig derivert på (1, ©о). Dette betyr at i henhold til Dirichlet-Abel-kriteriet konvergerer det andre integralet i (12.69), dvs. Fresnel-integralet konvergerer også.
Som du vet, kan det være en ganske vanskelig oppgave å finne integralen. Det ville være en stor skuffelse å begynne å beregne en upassende integral og finne på slutten av banen at den divergerer. Derfor er av interesse metoder som tillater, uten seriøse beregninger basert på en type funksjon, å trekke en konklusjon om konvergensen eller divergensen til et upassende integral. De første og andre sammenligningsteoremet, som vil bli diskutert nedenfor, hjelper i stor grad til å studere upassende integraler for konvergens.
La f(x)?0. Deretter funksjonene
er monotont økende i variablene t eller -g (siden vi tar g>0, tenderer -g til null fra venstre). Hvis, ettersom argumentene øker, funksjonene F 1 (t) og F 2 (-d) forblir avgrenset ovenfra, betyr dette at de tilsvarende upassende integralene konvergerer. Dette er grunnlaget for det første sammenligningsteoremet for integraler av ikke-negative funksjoner.
La funksjonene f(x) og g(x) ved x?a tilfredsstille følgende betingelser:
- 1) 0-f(x)-g(x);
- 2) Funksjonene f(x) og g(x) er kontinuerlige.
Så følger fra konvergensen av integralet integralets konvergens, og fra integralets divergens følger divergensen
Siden 0?f(x)?g(x) og funksjonene er kontinuerlige, da
Ved betingelse konvergerer integralet, dvs. har en endelig verdi. Derfor konvergerer også integralet.
La nå integralet divergere. La oss anta at integralet konvergerer, men da må integralet konvergere, noe som motsier betingelsen. Vår antagelse er feil, integralet divergerer.
Sammenligningsteorem for uekte integraler av 2. type.
La for funksjonene f(x) og g(x) på intervallet øke uten grense for x>+0. For x>+0 gjelder følgende ulikhet:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.
Sammenligningsteorem for uekte integraler av 1. type.
La funksjonen f(x) og g(x) være på intervallet , og integrasjonssegmentet er endelig, det vil si begrenset av tall og ikke av uendelig. Noen oppgaver fører til behovet for å forlate disse restriksjonene. Slik fremstår upassende integraler.
Geometrisk betydning av det upassende integralet Det viser seg ganske enkelt. I tilfellet når grafen til en funksjon y = f(x) er over aksen Okse, uttrykker det bestemte integralet arealet til en kurvelinjeformet trapes avgrenset av en kurve y = f(x) , x-akse og ordinater x = en , x = b. På sin side uttrykker det uriktige integralet arealet til en ubegrenset (uendelig) krumlinjet trapes som er innelukket mellom linjene y = f(x) (på bildet nedenfor - rødt), x = en og abscisseaksen.

Uriktige integraler er definert på samme måte for andre uendelige intervaller:
Arealet til en uendelig buet trapes kan være et endelig tall, i så fall kalles det upassende integralet konvergent. Området kan også være uendelig, og i dette tilfellet kalles det upassende integralet divergent.
Bruke grensen til en integral i stedet for den upassende integralen i seg selv. For å evaluere det upassende integralet, må du bruke grensen for det definitive integralet. Hvis denne grensen eksisterer og er endelig (ikke lik uendelig), kalles det upassende integralet konvergent, og ellers - divergent. Hva en variabel har en tendens til under grensetegnet avhenger av om vi har å gjøre med en upassende integral av den første typen eller av den andre typen. La oss finne ut om dette nå.
Upassende integraler av den første typen - med uendelige grenser og deres konvergens
Feil integraler med uendelig øvre grense
Så, å skrive et upassende integral skiller seg fra det vanlige bestemte integralet ved at den øvre grensen for integrasjon er uendelig.
Definisjon. En upassende integral med en uendelig øvre grense for integrering av en kontinuerlig funksjon f(x) i intervallet fra en før ∞ grensen for integralet til denne funksjonen med den øvre grensen for integrasjon kalles b og den nedre grensen for integrering en forutsatt at den øvre grensen for integrering vokser ubegrenset, dvs.
![]() .
.
Hvis denne grensen eksisterer og er lik et eller annet tall i stedet for uendelig, da et upassende integral kalles konvergent, og tallet som grensen er lik, tas som verdien. Ellers en upassende integral kalles divergent og ingen mening tilskrives det.
Eksempel 1. Beregn uriktig integral(hvis det konvergerer).
Løsning. Basert på definisjonen av det upassende integralet finner vi

Siden grensen eksisterer og er lik 1, så dette upassende integral konvergerer og er lik 1.
I det følgende eksempelet er integranden nesten den samme som i eksempel 1, bare graden x er ikke to, men bokstaven alfa, og oppgaven er å studere det upassende integralet for konvergens. Det vil si at spørsmålet gjenstår å besvare: ved hvilke verdier av alfa konvergerer denne upassende integralen, og til hvilke verdier divergerer den?
Eksempel 2. Undersøk det upassende integralet for konvergens(den nedre grensen for integrasjon er større enn null).
Løsning. La oss da først anta at

I det resulterende uttrykket beveger vi oss til grensen ved:
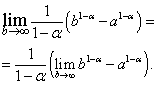
Det er lett å se at grensen på høyre side eksisterer og er lik null når , altså , og ikke eksisterer når , altså .
I det første tilfellet, det vil si når . Hvis da  og eksisterer ikke.
og eksisterer ikke.
Konklusjonen av vår studie er som følger: dette upassende integral konvergerer kl og divergerer kl.
Bruk av Newton-Leibniz-formelen på typen upassende integral som studeres ![]() , kan du utlede følgende formel, som er veldig lik den:
, kan du utlede følgende formel, som er veldig lik den:
 .
.
Dette er en generalisert Newton-Leibniz-formel.
Eksempel 3. Beregn uriktig integral(hvis det konvergerer).
Grensen for dette integralet eksisterer:
![]()
Det andre integralet, som utgjør summen som uttrykker det opprinnelige integralet:

Grensen for dette integralet eksisterer også:
![]() .
.
Vi finner summen av to integraler, som også er verdien av det opprinnelige upassende integralet med to uendelige grenser:
Upassende integraler av den andre typen - fra ubegrensede funksjoner og deres konvergens
La funksjonen f(x) gitt på segmentet fra en før b og er ubegrenset på det. Anta at funksjonen går til uendelig ved punktet b , mens den på alle andre punkter i segmentet er kontinuerlig.
Definisjon. En upassende integral av en funksjon f(x) på segmentet fra en før b grensen for integralet til denne funksjonen med den øvre grensen for integrasjon kalles c , hvis når du strever c Til b funksjonen øker uten grenser, og på punktet x = b funksjon ikke definert, dvs.
![]() .
.
Hvis denne grensen eksisterer, kalles det upassende integralet av den andre typen konvergent, ellers kalles det divergent.
Ved å bruke Newton-Leibniz-formelen utleder vi.
1. Uriktige integraler med uendelige grenser
La oss huske definisjonen av et integral som grensen for integralsummer: 
Definisjonen forutsetter at integrasjonsintervallet er endelig og funksjonen f(x) er kontinuerlig innenfor det. Brudd på disse forutsetningene fører til upassende integraler.
Definisjon. Hvis integralet tenderer til en begrenset grense når det øker i det uendelige "b", da kalles denne grensen et upassende integral med en uendelig øvre grense for funksjonen f (x) og er betegnet med symbolet 
I dette tilfellet sies det upassende integralet å eksistere eller konvergere.
Hvis den spesifiserte grensen ikke eksisterer eller eksisterer, men er uendelig, så sies integralet å ikke eksistere eller å divergere.
Et upassende integral med en uendelig nedre grense er definert på samme måte:

Et upassende integral med to uendelige grenser er gitt av:

hvor c er et hvilket som helst fast punkt på Ox-aksen.
Så uekte integraler kan ha en uendelig nedre grense, en uendelig øvre grense, og også to uendelige grenser.
Tegn på konvergens. Absolutt og betinget konvergens
Et integral eksisterer bare hvis hver av integralene eksisterer: og .
Eksempel. Undersøk konvergensen til integralet
Forutsatt at c = 0, får vi:

de. integralet konvergerer.
Noen ganger er det ikke nødvendig å beregne et upassende integral, men det er nok å bare vite om det konvergerer eller divergerer ved å sammenligne det med et annet integral.
Sammenligningsteorem for upassende integraler.
La funksjonen f (x) i intervallet ha flere (endelig antall) diskontinuitetspunkter av den første typen, denne "hindringen" kan enkelt elimineres ved å dele segmentet i flere segmenter med diskontinuitetspunkter, beregne bestemte integraler på hver enkelt seksjon og å legge sammen resultatene.
La oss vurdere det bestemte integralet til en funksjon som er ubegrenset når vi nærmer oss en av endene av segmentet, for eksempel, ![]() .
.
(I slike tilfeller sier de vanligvis: ''Funksjonen har en uendelig diskontinuitet i den høyre enden av integrasjonsintervallet.''.)
Det er tydelig at den vanlige definisjonen av et integral mister sin mening her.
Definisjon. Et upassende integral av funksjonen f(x), kontinuerlig for en £ x< b и неограниченной при x ® b - 0, называется предел:

Det upassende integralet til en funksjon som har en uendelig diskontinuitet i venstre ende av segmentet er definert på samme måte:

Følgelig divergerer integralet i seksjonen [-1, 0].

Dette betyr at integralet også divergerer i snittet.
Dermed divergerer dette integralet over hele intervallet [-1, 1]. Legg merke til at hvis vi begynte å beregne dette integralet uten å ta hensyn til diskontinuiteten til integranden i punktet x = 0, ville vi få et feil resultat. Egentlig,
 , som er umulig.
, som er umulig.
Så for å studere det upassende integralet til en diskontinuerlig funksjon, er det nødvendig å "dele" det i flere integraler og studere dem.
Hvis integranden har en diskontinuitet av den andre typen på det (endelige) integrasjonsintervallet, snakker vi om et upassende integral av den andre typen.
10.2.1 Definisjon og grunnleggende egenskaper
La oss angi integrasjonsintervallet med $\venstre[ a, \, b \right ]$; begge disse tallene antas å være endelige nedenfor. Hvis det bare er 1 diskontinuitet, kan den være plassert enten ved punkt $a$, eller ved punkt $b$, eller innenfor intervallet $(a,\,b)$. La oss først vurdere tilfellet når det er en diskontinuitet av den andre typen ved punkt $a$, og på andre punkter er integrandfunksjonen kontinuerlig. Så vi diskuterer integralen
\begin(equation) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(equation)
og $f(x) \rightarrow \infty $ når $x \rightarrow a+0$. Som før er den første tingen å gjøre å gi mening til dette uttrykket. For å gjøre dette, vurder integralen
\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]
Definisjon. La det være en begrenset grense
\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]
Deretter sies det upassende integralet av den andre typen (22) å konvergere og verdien $A$ tildeles det; funksjonen $f(x)$ i seg selv sies å være integrerbar på intervallet $\left[ a, \ , b\right]$.
Tenk på integralen
\[ I=\int ^1_0\frac(dx)(\sqrt(x)). \]
Integrandfunksjonen $1/\sqrt(x)$ ved $x \rightarrow +0$ har en uendelig grense, så ved punktet $x=0$ har den en diskontinuitet av den andre typen. La oss sette
\[ I(\epsilon)=\int ^1_(\epsilon )\frac(dx)(\sqrt(x))\,. \]
I i dette tilfellet antiderivatet er kjent,
\[ I(\epsilon)=\int ^1_(\epsilon )\frac(dx)(\sqrt(x))=2\sqrt(x)|^1_(\epsilon )=2(1-\sqrt( \epsilon ))\høyrepil 2\]
ved $\epsilon \rightarrow +0$. Dermed er det opprinnelige integralet et konvergent upassende integral av den andre typen, og det er lik 2.
La oss vurdere alternativet når det er en diskontinuitet av den andre typen i integrandfunksjonen ved den øvre grensen av integrasjonsintervallet. Dette tilfellet kan reduseres til det forrige ved å endre variabelen $x=-t$ og deretter omorganisere grensene for integrasjon.
La oss vurdere alternativet når integrandfunksjonen har en diskontinuitet av den andre typen inne i integrasjonsintervallet, ved punkt $c \in (a,\,b)$. I dette tilfellet den opprinnelige integralen
\begin(equation) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(equation)
presentert som en sum
\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]
Definisjon. Hvis begge integralene $I_1, \, I_2$ konvergerer, kalles det upassende integralet (23) konvergent og tildeles en verdi lik summen av integralene $I_1, \, I_2$, funksjonen $f(x)$ kalles integrerbar på intervallet $\venstre [a, \, b\right]$. Hvis minst ett av integralene $I_1,\, I_2$ er divergent, kalles det upassende integralet (23) divergent.
Konvergerende uekte integraler av 2. type har alle standardegenskapene til vanlige bestemte integraler.
1. Hvis $f(x)$, $g(x)$ er integrerbare på intervallet $\left[ a, \,b \right ]$, så er summen deres $f(x)+g(x)$ også integrerbar på dette intervallet, og \[ \int _a^(b)\venstre(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Hvis $f(x)$ er integrerbar på intervallet $\left[ a, \, b \right ]$, så er funksjonen $C\cdot f(x)$ for enhver konstant $C$ også integrerbar på dette intervallet , og \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Hvis $f(x)$ er integrerbar på intervallet $\left[ a, \, b \right ]$, og på dette intervallet $f(x)>0$, så \[ \int _a^ (b) f(x)dx\,>\,0. \] 4. Hvis $f(x)$ er integrerbar på intervallet $\left[ a, \, b \right ]$, så for enhver $c\in (a, \,b)$ integralene \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] konvergerer også, og \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (additivitet av integralet over intervallet).
Tenk på integralen \begin(ligning) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(ligning) Hvis $k>0$, har integranden en tendens til $\infty$ som $x \rightarrow +0$, så integralet er upassende av den andre typen. La oss introdusere funksjonen \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \] I dette tilfellet er antiderivatet kjent, så \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k) )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \] for $k \neq 1$, \[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \] for $k = 1$. Tatt i betraktning atferden ved $\epsilon \rightarrow +0$, kommer vi til den konklusjon at integral (20) konvergerer ved $k
10.2.2 Tester for konvergens av upassende integraler av den andre typen
Teorem (det første tegnet på sammenligning). La $f(x)$, $g(x)$ være kontinuerlige for $x\in (a,\,b)$ og $0 1. Hvis integralet \[ \int _a^(b)g(x) dx \] konvergerer, så konvergerer integralet \[ \int _a^(b)f(x)dx. \] 2. Hvis integralet \[ \int _a^(b)f(x)dx \] divergerer, divergerer integralet \[ \int _a^(b)g(x)dx. \]
Teorem (andre sammenligningskriterium). La $f(x)$, $g(x)$ være kontinuerlige og positive for $x\in (a,\,b)$, og la det være en begrenset grense
\[ \theta = \lim_(x \høyrepil a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]
Deretter integralene
\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]
konvergere eller divergere samtidig.
Tenk på integralen
\[ I=\int _0^(1)\frac(1)(x+\sin x)\,dx. \]
Integranden er en positiv funksjon på integrasjonsintervallet, integranden har en tendens til $\infty$ som $x \rightarrow +0$, så integralet vårt er et upassende integral av den andre typen. Videre, for $x \rightarrow +0$ har vi: hvis $g(x)=1/x$, så
\[ \lim _(x \høyrepil +0)\frac(f(x))(g(x))=\lim _(x \høyrepil +0)\frac(x)(x+\sin x)=\ frac(1)(2) \nev 0,\, \infty \, . \]
Ved å bruke det andre sammenligningskriteriet kommer vi til den konklusjon at integralet vårt konvergerer eller divergerer samtidig med integralet
\[ \int _0^(+1)\frac(1)(x)\,dx . \]
Som det ble vist i forrige eksempel, divergerer dette integralet ($k=1$). Følgelig divergerer også det opprinnelige integralet.
Beregn det upassende integralet eller finn dets konvergens (divergens).
1. \[ \int _(0)^(1)\frac(dx)(x^3-5x^2)\,. \] 2. \[ \int _(3)^(7)\frac(x\,dx)((x-5)^2)\,. \] 3. \[ \int _(0)^(1)\frac(x\,dx)(\sqrt(1-x^2))\,. \] 4. \[ \int _(0)^(1)\frac(x^3\,dx)(1-x^5)\,. \] 5. \[ \int _(-3)^(2)\frac(dx)((x+3)^2)\,. \] 6. \[ \int _(1)^(2)\frac(x^2\,dx)((x-1)\sqrt(x-1))\,. \] 7. \[ \int _(0)^(1)\frac(dx)(\sqrt(x+x^2))\,. \] 8. \[ \int _(0)^(1/4)\frac(dx)(\sqrt(x-x^2))\,. \] 9. \[ \int _(1)^(2)\frac(dx)(xlnx)\,. \] 10. \[ \int _(1)^(2)\frac(x^3\,dx)(\sqrt(4-x^2))\,. \] 11. \[ \int _(0)^(\pi /4)\frac(dx)(\sin ^4x)\,. \]