Sa është shuma e këndeve? Teorema mbi shumën e këndeve të një trekëndëshi. Llojet sipas madhësisë së këndit

Shuma e këndeve të trekëndëshit- e rëndësishme, por mjaft temë e thjeshtë, e cila mësohet në klasën e 7-të gjeometria. Tema përbëhet nga një teoremë, një provë e shkurtër dhe disa pasoja logjike. Njohja e kësaj teme ndihmon në zgjidhje problemet gjeometrike gjatë studimit të mëvonshëm të lëndës.

Teorema - cilat janë këndet e një trekëndëshi arbitrar të mbledhur së bashku?

Teorema thotë se nëse merrni ndonjë trekëndësh, pavarësisht nga lloji i tij, shuma e të gjithë këndeve do të jetë pa ndryshim 180 gradë. Kjo vërtetohet si më poshtë:

• për shembull, merrni trekëndëshin ABC, vizatoni një vijë të drejtë përmes pikës B të vendosur në majë dhe caktoni atë si "a", drejtëza "a" është rreptësisht paralele me anën AC;
• midis drejtëzës "a" dhe brinjëve AB dhe BC, caktohen kënde, duke i shënuar me numrat 1 dhe 2;
• këndi 1 konsiderohet i barabartë me këndin A, dhe këndi 2 konsiderohet i barabartë me këndin C, pasi këto kënde konsiderohen të shtrihen në mënyrë tërthore;
• Kështu, shuma midis këndeve 1, 2 dhe 3 (e cila është caktuar në vend të këndit B) njihet si e barabartë me këndin e shpalosur me kulmin B - dhe është 180 gradë.

Nëse shuma e këndeve të treguara me numra është 180 gradë, atëherë shuma e këndeve A, B dhe C njihet si e barabartë me 180 gradë. Ky rregull është i vërtetë për çdo trekëndësh.

Çfarë rrjedh nga teorema gjeometrike

Është e zakonshme të theksohen disa përfundime nga teorema e mësipërme.

• Nëse problemi shqyrton një trekëndësh me një kënd të drejtë, atëherë një nga këndet e tij do të jetë i barabartë me 90 gradë si parazgjedhje, dhe shuma e këndeve akute do të jetë gjithashtu 90 gradë.
• Nëse po flasim për një trekëndësh të drejtë izosceles, atëherë këndet e tij akute, të cilat shtohen deri në 90 gradë, individualisht do të jenë të barabarta me 45 gradë.
• Një trekëndësh barabrinjës përbëhet nga tre kënde të barabarta, përkatësisht, secili prej tyre do të jetë i barabartë me 60 gradë, dhe në total do të jetë 180 gradë.
• Këndi i jashtëm i çdo trekëndëshi do të jetë i barabartë me shumën midis dy këndeve të brendshme që nuk janë ngjitur me të.

Mund të nxirret rregulli i mëposhtëm: çdo trekëndësh ka të paktën dy kënde akute. Në disa raste, një trekëndësh përbëhet nga tre kënde akute, dhe nëse ka vetëm dy, atëherë këndi i tretë do të jetë i mpirë ose i drejtë.

Teorema. Shuma e këndeve të brendshme të një trekëndëshi është e barabartë me dy kënde të drejta.

Le të marrim një trekëndësh ABC (Fig. 208). Le t'i shënojmë këndet e tij të brendshme me numrat 1, 2 dhe 3. Le ta vërtetojmë këtë

∠1 + ∠2 + ∠3 = 180°.

Le të vizatojmë përmes një kulmi të trekëndëshit, për shembull B, një vijë të drejtë MN paralele me AC.

Në kulmin B kemi tre kënde: ∠4, ∠2 dhe ∠5. Shuma e tyre është një kënd i drejtë, prandaj është e barabartë me 180°:

∠4 + ∠2 + ∠5 = 180°.

Por ∠4 = ∠1 janë kënde të brendshme tërthore me drejtëza paralele MN dhe AC dhe sekant AB.

∠5 = ∠3 - këto janë kënde të brendshme tërthore me drejtëza paralele MN dhe AC dhe sekante BC.

Kjo do të thotë se ∠4 dhe ∠5 mund të zëvendësohen nga barazimet e tyre ∠1 dhe ∠3.

Prandaj, ∠1 + ∠2 + ∠3 = 180°. Teorema është e vërtetuar.

2. Veti e këndit të jashtëm të trekëndëshit.

Në fakt, në trekëndëshin ABC (Fig. 209) ∠1 + ∠2 = 180° - ∠3, por edhe ∠ВСD, këndi i jashtëm i këtij trekëndëshi, jo ngjitur me ∠1 dhe ∠2, është gjithashtu i barabartë me 180° - ∠3.

Kështu:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Prandaj, ∠1 + ∠2= ∠BCD.

Vetia e prejardhur e këndit të jashtëm të një trekëndëshi sqaron përmbajtjen e teoremës së provuar më parë mbi këndin e jashtëm të një trekëndëshi, e cila deklaroi vetëm se këndi i jashtëm i një trekëndëshi është më i madh se çdo kënd i brendshëm i një trekëndëshi jo ngjitur me të; tani është vërtetuar se këndi i jashtëm është i barabartë me shumën e të dy këndeve të brendshëm që nuk janë ngjitur me të.

3. Veti e trekëndëshit kënddrejtë me kënd 30°.

Le të jetë këndi B në trekëndëshin kënddrejtë ACB i barabartë me 30° (Fig. 210). Atëherë këndi tjetër i tij akut do të jetë i barabartë me 60°.

Le të vërtetojmë se këmba AC është e barabartë me gjysmën e hipotenuzës AB. Le të zgjasim këmbën AC përtej kulmit të këndit të drejtë C dhe të lëmë mënjanë një segment CM të barabartë me segmentin AC. Le të lidhim pikën M me pikën B. Trekëndëshi që rezulton ВСМ është i barabartë me trekëndëshin ACB. Shohim se çdo kënd i trekëndëshit ABM është i barabartë me 60°, prandaj ky trekëndësh është trekëndësh barabrinjës.

Këmba AC është e barabartë me gjysmën e AM, dhe meqenëse AM është e barabartë me AB, këmba AC do të jetë e barabartë me gjysmën e hipotenuzës AB.

Shuma e këndeve të brendshme të një trekëndëshi është 180 0. Kjo është një nga aksiomat themelore të gjeometrisë së Euklidit. Kjo është gjeometria që studiojnë nxënësit e shkollës. Gjeometria përkufizohet si shkenca që studion format hapësinore të botës reale.

Çfarë i motivoi grekët e lashtë të zhvillonin gjeometrinë? Nevoja për të matur fusha, livadhe - zona të sipërfaqes së tokës. Në të njëjtën kohë, grekët e lashtë pranuan se sipërfaqja e Tokës ishte horizontale dhe e sheshtë. Duke marrë parasysh këtë supozim, u krijuan aksiomat e Euklidit, duke përfshirë shumën e këndeve të brendshme të një trekëndëshi prej 180 0.

Një aksiomë është një propozim që nuk kërkon provë. Si duhet kuptuar kjo? Shprehet një dëshirë që i përshtatet personit dhe më pas vërtetohet me ilustrime. Por gjithçka që nuk është vërtetuar është trillim, diçka që nuk ekziston në realitet.

Marrja sipërfaqen e tokës horizontale, grekët e lashtë automatikisht e pranuan formën e Tokës si të sheshtë, por ajo është e ndryshme - sferike. Nuk ka fare plane horizontale apo vija të drejta në natyrë, sepse graviteti përkul hapësirën. Vijat e drejta dhe rrafshet horizontale gjenden vetëm në trurin e njeriut.

Prandaj, gjeometria e Euklidit, e cila shpjegon format hapësinore të botës imagjinare, është një simulacrum - një kopje që nuk ka origjinal.

Një nga aksiomat e Euklidit thotë se shuma e këndeve të brendshme të një trekëndëshi është 180 0. Në fakt, në hapësirën reale të lakuar, ose në sipërfaqen sferike të Tokës, shuma e këndeve të brendshme të një trekëndëshi është gjithmonë më e madhe se 180 0.

Le të mendojmë kështu. Çdo meridian në glob kryqëzohet me ekuatorin në një kënd prej 90 0. Për të marrë një trekëndësh, duhet të largoni një meridian tjetër nga meridiani. Shuma e këndeve të trekëndëshit ndërmjet meridianëve dhe anës së ekuatorit do të jetë 180 0. Por do të ketë ende një kënd në pol. Si rezultat, shuma e të gjitha këndeve do të jetë më shumë se 180 0.

Nëse anët kryqëzohen në një kënd prej 90 0 në pol, atëherë shuma e këndeve të brendshme të një trekëndëshi të tillë do të jetë 270 0. Dy meridianë që kryqëzojnë ekuatorin në kënde të drejta në këtë trekëndësh do të jenë paralel me njëri-tjetrin, dhe në polin që kryqëzojnë njëri-tjetrin në një kënd prej 90 0 do të bëhen pingul. Rezulton se dy drejtëza paralele në të njëjtin rrafsh jo vetëm që kryqëzohen, por mund të jenë edhe pingule në pol.

Natyrisht, anët e një trekëndëshi të tillë nuk do të jenë vija të drejta, por konveks, duke përsëritur formën sferike globit. Por kjo është pikërisht bota reale e hapësirës.

Gjeometria e hapësirës reale, duke marrë parasysh lakimin e saj në mesin e shekullit të 19-të. zhvilluar nga matematikani gjerman B. Riemann (1820-1866). Por nxënësve të shkollës nuk u thuhet për këtë.

Pra, gjeometria Euklidiane, e cila merr formën e Tokës si e sheshtë me një sipërfaqe horizontale, e cila në fakt nuk është, është një simulakrum. Nootic është gjeometria Riemanniane që merr parasysh lakimin e hapësirës. Shuma e këndeve të brendshme të trekëndëshit në të është më e madhe se 180 0.

Dëshmi

Le ABC" - trekëndësh arbitrar. Le të ecim në krye B drejtëza paralele me drejtëzën A.C. (një vijë e tillë e drejtë quhet drejtëza Euklidiane). Le të shënojmë një pikë në të D në mënyrë që pikat A Dhe D shtrihen në anët e kundërta të një vije të drejtë B.C..Këndet DBC Dhe ACB e barabartë me shtrirjen e brendshme tërthore e formuar nga një sekant B.C. me vija paralele A.C. Dhe BD. Prandaj, shuma e këndeve të një trekëndëshi në kulmet B Dhe ME e barabartë me këndin ABD.Shuma e të tre këndeve të një trekëndëshi është e barabartë me shumën e këndeve ABD Dhe BAC. Meqenëse këto kënde janë të brendshme të njëanshme për paralele A.C. Dhe BD në sekant AB, atëherë shuma e tyre është 180°. Teorema është e vërtetuar.

Pasojat

Nga teorema rrjedh se çdo trekëndësh ka dy kënde akute. Në të vërtetë, duke përdorur vërtetimin me kontradiktë, le të supozojmë se trekëndëshi ka vetëm një kënd të mprehtë ose nuk ka fare kënd të mprehtë. Atëherë ky trekëndësh ka të paktën dy kënde, secili prej të cilëve është të paktën 90°. Shuma e këtyre këndeve nuk është më e vogël se 180°. Por kjo është e pamundur, pasi shuma e të gjithë këndeve të një trekëndëshi është 180°. Q.E.D.

Përgjithësimi në teorinë e Simpleksit

Ku është këndi ndërmjet faqeve i dhe j të simpleksit.

Shënime

• Në një sferë, shuma e këndeve të një trekëndëshi gjithmonë tejkalon 180 °, ndryshimi quhet tepricë sferike dhe është proporcionale me sipërfaqen e trekëndëshit.
• Në rrafshin Lobachevsky, shuma e këndeve të një trekëndëshi është gjithmonë më e vogël se 180°. Dallimi është gjithashtu proporcional me sipërfaqen e trekëndëshit.

Shiko gjithashtu

Fondacioni Wikimedia. 2010.

Shihni se çfarë është "Teorema mbi shumën e këndeve të një trekëndëshi" në fjalorë të tjerë:

Vetia e shumëkëndëshave në gjeometrinë Euklidiane: Shuma e këndeve n të një trekëndëshi është 180°(n 2). Përmbajtja 1 Prova 2 Shënim ... Wikipedia

Teorema e Pitagorës është një nga teoremat themelore të gjeometrisë Euklidiane, duke vendosur marrëdhëniet midis brinjëve të një trekëndëshi kënddrejtë. Përmbajtja 1 ... Wikipedia

Teorema e Pitagorës është një nga teoremat themelore të gjeometrisë Euklidiane, duke vendosur marrëdhëniet midis brinjëve të një trekëndëshi kënddrejtë. Përmbajtja 1 Deklarata 2 Dëshmi ... Wikipedia

Teorema e kosinusit është një përgjithësim i teoremës së Pitagorës. Katrori i brinjës së trekëndëshit është i barabartë me shumën e katrorëve të dy brinjëve të tjera të tij pa dyfishin e produktit të këtyre brinjëve nga kosinusi i këndit ndërmjet tyre. Për një trekëndësh të rrafshët me anët a,b,c dhe këndi α... ... Wikipedia

Ky term ka kuptime të tjera, shiko Trekëndëshi (kuptimet). Një trekëndësh (në hapësirën Euklidiane) është figura gjeometrike, i formuar nga tre segmente që lidhin tre pika që nuk shtrihen në të njëjtën vijë të drejtë. Tre pika,... ...Wikipedia

Shënim standard Një trekëndësh është shumëkëndëshi më i thjeshtë që ka 3 kulme (kënde) dhe 3 brinjë; pjesë e rrafshit e kufizuar nga tre pika që nuk shtrihen në të njëjtën vijë dhe tre segmente që i lidhin këto pika në çift. Kulmet e një trekëndëshi ... Wikipedia

Matematikan i lashtë grek. Punoi në Aleksandri në shekullin III. para Krishtit e. Puna kryesore"Principia" (15 libra), që përmban themelet e matematikës antike, gjeometrisë elementare, teorisë së numrave, teori e përgjithshme marrëdhëniet dhe metodat për përcaktimin e sipërfaqeve dhe vëllimeve,... ... fjalor enciklopedik

- (vdiq midis viteve 275 dhe 270 p.e.s.) matematikan i lashtë grek. Informacioni për kohën dhe vendin e lindjes së tij nuk ka arritur tek ne, por dihet se Euklidi ka jetuar në Aleksandri dhe lulëzimi i veprimtarisë së tij ka ndodhur gjatë mbretërimit të Ptolemeut I në Egjipt... ... Fjalori i madh enciklopedik

Gjeometria e ngjashme me gjeometrinë Euklidiane në atë që përcakton lëvizjen e figurave, por ndryshon nga gjeometria Euklidiane në atë që një nga pesë postulatet e saj (i dyti ose i pesti) zëvendësohet nga mohimi i tij. Mohimi i njërit prej postulateve Euklidiane... ... Enciklopedia e Collier

Trekëndëshi . Trekëndësh i mprehtë, i mpirë dhe kënddrejtë.

Këmbët dhe hipotenuza. Trekëndëshi dykëndësh dhe barabrinjës.

Shuma e këndeve të një trekëndëshi.

Këndi i jashtëm i një trekëndëshi. Shenjat e barazisë së trekëndëshave.

Linjat dhe pikat e jashtëzakonshme në një trekëndësh: lartësitë, mesataret,

përgjysmues, mesatarja e pingul, ortoqendër,

qendra e gravitetit, qendra e një rrethi të rrethuar, qendra e një rrethi të brendashkruar.

Teorema e Pitagorës. Raporti i pamjes në një trekëndësh arbitrar.

Trekëndëshi është një shumëkëndësh me tre brinjë (ose tre kënde). Anët e një trekëndëshi shpesh tregohen me shkronja të vogla që korrespondojnë me shkronja të mëdha, duke treguar kulme të kundërta.

Nëse të tre këndet janë akute (Fig. 20), atëherë kjo është trekëndëshi akut . Nëse njëri nga këndet është i drejtë(C, Fig.21), kjo eshte trekëndësh kënddrejtë; anëta, bduke formuar një kënd të drejtë quhen këmbët; anësorcpërballë këndit të drejtë quhet hipotenuzë. Nëse një nga kënde të mpirë (B, Fig. 22), kjo eshte trekëndësh i mpirë.


Trekëndëshi ABC (Fig. 23) - izosceles, Nëse dy anët e tij janë të barabarta (a= c); quhen këto anë të barabarta anësore, quhet i treti bazë trekëndëshi. Trekëndëshi ABC (Fig. 24) - barabrinjës, Nëse Të gjitha anët e tij janë të barabarta (a = b = c). Në përgjithësi ( a ≠ b ≠ c) ne kemi scalene trekëndëshi .

Vetitë themelore të trekëndëshave. Në çdo trekëndësh:

1. Përballë anës më të madhe shtrihet këndi më i madh dhe anasjelltas.

2. Këndet e barabarta shtrihen përballë brinjëve të barabarta, dhe anasjelltas.

Në veçanti, të gjitha këndet në barabrinjës trekëndëshat janë të barabartë.

3. Shuma e këndeve të një trekëndëshi është 180 º .

Nga dy vetitë e fundit rezulton se çdo kënd në një barabrinjës

trekëndëshi është 60 º.

4. Vazhdimi i njërës nga brinjët e trekëndëshit (AC, Fig. 25), marrim e jashtme

këndi BCD . Këndi i jashtëm i një trekëndëshi është i barabartë me shumën e këndeve të brendshme,

jo ngjitur me të : BCD = A + B.

5. Çdo brinja e një trekëndëshi është më e vogël se shuma e dy brinjëve të tjera dhe më e madhe

dallimet e tyre (a < b + c, a > b – c;b < a + c, b > a – c;c < a + b,c > a – b).

Shenjat e barazisë së trekëndëshave.

Trekëndëshat janë kongruentë nëse janë përkatësisht të barabartë:

a ) dy brinjë dhe këndi ndërmjet tyre;

b ) dy qoshe dhe ana ngjitur me to;

c) tre anët.

Shenjat e barazisë së trekëndëshave kënddrejtë.

Dy drejtkëndëshe trekëndëshat janë të barabartë nëse një nga kushtet e mëposhtme është i vërtetë:

1) këmbët e tyre janë të barabarta;

2) këmba dhe hipotenuza e njërit trekëndësh janë të barabarta me këmbën dhe hipotenuzën e tjetrit;

3) hipotenuza dhe këndi akut i njërit trekëndësh janë të barabartë me hipotenuzën dhe këndin akut të tjetrit;

4) këmba dhe këndi akut ngjitur i njërit trekëndësh janë të barabartë me këmbën dhe këndin akut ngjitur të tjetrit;

5) këmba dhe këndi i kundërt akut i një trekëndëshi janë të barabartë me këmbën dhe këndi i kundërt akut i tjetrit.

Vija dhe pika të mrekullueshme në trekëndësh.

Lartësia trekëndëshi ështëpingul,ulet nga çdo kulm në anën e kundërt ( ose vazhdimi i tij). Kjo anë quhetbaza e trekëndëshit . Tri lartësitë e një trekëndëshi gjithmonë kryqëzohennë një moment, thirri ortoqendër trekëndëshi. Ortoqendra e një trekëndëshi akut (pika O , Fig. 26) ndodhet brenda trekëndëshit, dheortoqendra e një trekëndëshi të mpirë (pika O , fig.27) – jashtë; Ortoqendra e një trekëndëshi kënddrejtë përkon me kulmin e këndit të drejtë.

mesatare - Kjo segmenti i linjës , duke lidhur çdo kulm të një trekëndëshi me mesin e anës së kundërt. Tre median e një trekëndëshi (AD, BE, CF, fig.28) kryqëzohen në një pikë O , gjithmonë i shtrirë brenda trekëndëshit dhe duke qenë e tij qendra e gravitetit. Kjo pikë e ndan çdo mesatare në një raport 2:1, duke llogaritur nga kulmi.

përgjysmues - Kjo segment përgjysmues këndi nga kulmi në pikë kryqëzimet me anën e kundërt. Tre përgjysmues të një trekëndëshi (AD, BE, CF, fig.29) kryqëzohen në një pikë Oh, gjithmonë i shtrirë brenda trekëndëshit Dhe duke qenë qendra e rrethit të brendashkruar(shih seksionin "Të shkruaradhe shumëkëndëshat e rrethuar").

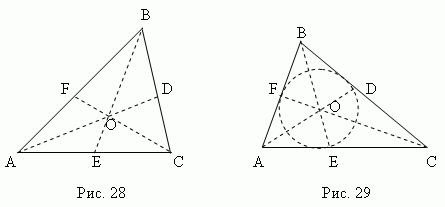
Përgjysmuesja e ndan anën e kundërt në pjesë proporcionale me anët ngjitur ; për shembull, në figurën 29 AE: CE = AB: BC.

Mesore pingul është një pingul i tërhequr nga mesi pikat e segmentit (anët). Tre përgjysmues pingul të trekëndëshit ABC(KO, MO, JO, Fig. 30 ) kryqëzohen në një pikë O, që është qendër rrethi i rrethuar (pikat K, M, N – mesi i brinjëve të trekëndëshit ABC).

Në një trekëndësh akut, kjo pikë shtrihet brenda trekëndëshit; në obtuse - jashtë; në një formë drejtkëndëshe - në mes të hipotenuzës. Ortoqendra, qendra e gravitetit, rrethi dhe rrethi i brendashkruar përkojnë vetëm në një trekëndësh barabrinjës.

Teorema e Pitagorës. Në një trekëndësh kënddrejtë, katrori i gjatësisëHipotenuza është e barabartë me shumën e katrorëve të gjatësisë së këmbëve.

Vërtetimi i teoremës së Pitagorës rrjedh qartë nga Fig. 31. Konsideroni një trekëndësh kënddrejtë ABC me këmbë a, b dhe hipotenuzë c.

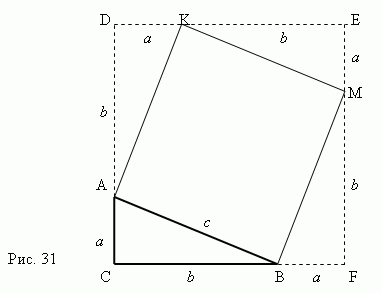
Le të ndërtojmë një shesh AKMB duke përdorur hipotenuzën AB si anë. Pastajvazhdoni brinjët e trekëndëshit kënddrejtë ABC në mënyrë që të merret një katror CDEF , ana e të cilit është e barabartëa + b .Tani është e qartë se zona e sheshit CDEF është e barabartë me ( a+b) 2 . Nga ana tjetër, kjo sipërfaqja është e barabartë me shumën zonave katër trekëndësha kënddrejtë dhe sheshi AKMB, pra

c 2 + 4 (ab / 2) = c 2 + 2 ab,

nga këtu,

c 2 + 2 ab= (a+b) 2 ,

dhe ne fund kemi:

c 2 =a 2 +b 2 .

Raporti i pamjes në një trekëndësh arbitrar.

Në rastin e përgjithshëm (për një trekëndësh arbitrar) kemi:

c 2 =a 2 +b 2 – 2ab· cos C,

ku C – këndi ndërmjet anëvea Dhe b .