Si të përcaktohet shenja e projeksionit në një bosht. Formulat bazë për gjetjen e distancave duke përdorur projeksionin e një vektori në një bosht. Prodhimi vektorial i vektorëve të njësive koordinative

§ 3. Projeksionet e një vektori në boshtet koordinative

1. Gjetja e projeksioneve gjeometrikisht.

Vektor
- projeksioni i vektorit mbi bosht OK
- projeksioni i vektorit mbi bosht OY

Përkufizimi 1. Projeksioni vektorial në çdo bosht koordinativ është një numër i marrë me një shenjë plus ose minus, që korrespondon me gjatësinë e segmentit të vendosur midis bazave të pinguleve të rënë nga fillimi dhe fundi i vektorit në boshtin koordinativ.

Shenja e projeksionit përcaktohet si më poshtë. Nëse, kur lëvizni përgjatë boshtit të koordinatave, ka një lëvizje nga pika e projektimit të fillimit të vektorit në pikën e projektimit të fundit të vektorit në drejtimin pozitiv të boshtit, atëherë projeksioni i vektorit konsiderohet pozitiv. . Nëse është e kundërt me boshtin, atëherë projeksioni konsiderohet negativ.

Figura tregon se nëse vektori është i orientuar disi i kundërt me boshtin koordinativ, atëherë projeksioni i tij në këtë bosht është negativ. Nëse një vektor është i orientuar disi në drejtimin pozitiv të boshtit të koordinatave, atëherë projeksioni i tij në këtë bosht është pozitiv.

Nëse një vektor është pingul me boshtin koordinativ, atëherë projeksioni i tij në këtë bosht është zero.
Nëse një vektor është në bashkëdrejtim me një bosht, atëherë projeksioni i tij në këtë bosht është i barabartë me vlerën absolute të vektorit.
Nëse një vektor drejtohet në të kundërt me boshtin koordinativ, atëherë projeksioni i tij në këtë bosht është i barabartë në vlerë absolute me vlerën absolute të vektorit të marrë me shenjën minus.

2. Shumica përkufizim i përgjithshëm projeksionet.

Nga një trekëndësh kënddrejtë ABD: .

Përkufizimi 2. Projeksioni vektorial në çdo bosht koordinativ është një numër i barabartë me prodhimin e modulit të vektorit dhe kosinusit të këndit të formuar nga vektori me drejtimin pozitiv të boshtit të koordinatave.

Shenja e projeksionit përcaktohet nga shenja e kosinusit të këndit të formuar nga vektori me drejtim të boshtit pozitiv.
Nëse këndi është akut, atëherë kosinusi ka një shenjë pozitive dhe projeksionet janë pozitive. Për këndet e mpirë, kosinusi ka një shenjë negative, kështu që në raste të tilla projeksionet në bosht janë negative.
- pra, për vektorët pingul me boshtin, projeksioni është zero.

Në fizikë për klasën 9 (I.K.Kikoin, A.K.Kikoin, 1999),
detyrë №5
te kapitulli " KAPITULLI 1. INFORMACION I PËRGJITHSHËM RRETH TRAFIKUT».

1. Si quhet projeksioni i një vektori në boshtin koordinativ?

1. Projeksioni i vektorit a në boshtin koordinativ është gjatësia e segmentit ndërmjet projeksioneve të fillimit dhe fundit të vektorit a (perpendikularët e rënë nga këto pika në bosht) në këtë bosht koordinativ.

2. Si lidhet vektori i zhvendosjes së një trupi me koordinatat e tij?

2. Projeksionet e vektorit të zhvendosjes s në boshtet e koordinatave janë të barabarta me ndryshimin e koordinatave të trupit përkatës.

3. Nëse koordinata e një pike rritet me kalimin e kohës, atëherë çfarë shenje ka projeksioni i vektorit të zhvendosjes në boshtin koordinativ? Po sikur të ulet?

3. Nëse koordinata e një pike rritet me kalimin e kohës, atëherë projeksioni i vektorit të zhvendosjes në boshtin koordinativ do të jetë pozitiv, sepse në këtë rast do të kalojmë nga projeksioni i fillimit në projeksionin e fundit të vektorit në drejtim të vetë boshtit.

Nëse koordinata e një pike zvogëlohet me kalimin e kohës, atëherë projeksioni i vektorit të zhvendosjes në boshtin koordinativ do të jetë negativ, sepse në këtë rast do të kalojmë nga projeksioni i fillimit në projeksionin e fundit të vektorit kundrejt udhëzuesit të vetë boshtit.

4. Nëse vektori i zhvendosjes është paralel me boshtin X, atëherë sa është moduli i projeksionit të vektorit në këtë bosht? Po moduli i projeksionit të të njëjtit vektor në boshtin Y?

4. Nëse vektori i zhvendosjes është paralel me boshtin X, atëherë moduli i projeksionit të vektorit në këtë bosht është i barabartë me modulin e vetë vektorit dhe projeksioni i tij në boshtin Y është zero.

5. Përcaktoni shenjat e projeksioneve në boshtin X të vektorëve të zhvendosjes të paraqitur në figurën 22. Si ndryshojnë koordinatat e trupit gjatë këtyre zhvendosjeve?

5. Në të gjitha rastet e mëposhtme, koordinata Y e trupit nuk ndryshon dhe koordinata X e trupit do të ndryshojë si më poshtë:

a) s 1;

projeksioni i vektorit s 1 në boshtin X është negativ dhe është i barabartë në vlerë absolute me gjatësinë e vektorit s 1 . Me një lëvizje të tillë, koordinata X e trupit do të zvogëlohet për gjatësinë e vektorit s 1.

b) s 2 ;

projeksioni i vektorit s 2 në boshtin X është pozitiv dhe i barabartë në madhësi me gjatësinë e vektorit s 1 . Me një lëvizje të tillë, koordinata X e trupit do të rritet me gjatësinë e vektorit s 2.

c) s 3;

projeksioni i vektorit s 3 në boshtin X është negativ dhe i barabartë në madhësi me gjatësinë e vektorit s 3 . Me një lëvizje të tillë, koordinata X e trupit do të zvogëlohet për gjatësinë e vektorit s 3.

d)s 4;

projeksioni i vektorit s 4 në boshtin X është pozitiv dhe i barabartë në madhësi me gjatësinë e vektorit s 4 . Me një lëvizje të tillë, koordinata X e trupit do të rritet me gjatësinë e vektorit s 4.

e) s 5;

projeksioni i vektorit s 5 në boshtin X është negativ dhe i barabartë në madhësi me gjatësinë e vektorit s 5 . Me një lëvizje të tillë, koordinata X e trupit do të zvogëlohet për gjatësinë e vektorit s 5.

6. Nëse vlera e distancës së përshkuar është e madhe, atëherë moduli i zhvendosjes a mund të jetë i vogël?

6. Ndoshta. Kjo për faktin se zhvendosja (vektori i zhvendosjes) është një sasi vektoriale, d.m.th. është një segment i drejtë i drejtuar që lidh pozicionin fillestar të trupit me pozicionet e tij pasuese. Dhe pozicioni përfundimtar i trupit (pavarësisht distancës së përshkuar) mund të jetë sa më afër pozicionit fillestar të trupit. Nëse pozicionet përfundimtare dhe fillestare të trupit përkojnë, moduli i zhvendosjes do të jetë i barabartë me zero.

7. Pse vektori i lëvizjes së një trupi është më i rëndësishëm në mekanikë sesa rruga që ka përshkuar?

7. Detyra kryesore e mekanikës është të përcaktojë pozicionin e trupit në çdo kohë. Duke ditur vektorin e lëvizjes së trupit, mund të përcaktojmë koordinatat e trupit, d.m.th. pozicionin e trupit në çdo moment në kohë, dhe duke ditur vetëm distancën e përshkuar, ne nuk mund të përcaktojmë koordinatat e trupit, sepse ne nuk kemi informacion për drejtimin e lëvizjes, por mund të gjykojmë vetëm gjatësinë e shtegut të përshkuar në një kohë të caktuar.

Boshti është drejtimi. Kjo do të thotë që projeksioni në një bosht ose në një vijë të drejtuar konsiderohet i njëjtë. Projeksioni mund të jetë algjebrik ose gjeometrik. Në terma gjeometrikë, projeksioni i një vektori në një bosht kuptohet si një vektor, dhe në terma algjebrikë kuptohet si një numër. Kjo do të thotë, përdoren konceptet e projeksionit të një vektori në një bosht dhe projeksioni numerik i një vektori në një bosht.

Nëse kemi një bosht L dhe një vektor jozero A B →, atëherë mund të ndërtojmë një vektor A 1 B 1 ⇀, duke treguar projeksionet e pikave të tij A 1 dhe B 1.

A 1 B → 1 do të jetë projeksioni i vektorit A B → në L.

Përkufizimi 1

Projeksioni i vektorit mbi boshtështë një vektor, fillimi dhe fundi i të cilit janë projeksione të fillimit dhe të fundit të një vektori të caktuar. n p L A B → → është zakon të shënohet projeksioni A B → në L. Për të ndërtuar një projeksion në L, pingulet hidhen në L.

Shembulli 1

Një shembull i një projeksioni vektori në një bosht.

Aktiv plan koordinativ Rreth x y është specifikuar pika M 1 (x 1 , y 1). Është e nevojshme të ndërtohen projeksione në Ox dhe O y për të imazhuar vektorin e rrezes së pikës M 1. Marrim koordinatat e vektorëve (x 1, 0) dhe (0, y 1).

Nëse bëhet fjalë për projeksionin e a → në një b jozero → ose për projeksionin e a → në drejtimin b → , atëherë nënkuptojmë projeksionin e a → në boshtin me të cilin drejtimi b → përkon. Projeksioni i a → në vijën e përcaktuar nga b → caktohet n p b → a → → . Dihet se kur këndi ndërmjet a → dhe b → , n p b → a → → dhe b → mund të konsiderohet bashkëdrejtues. Në rastin kur këndi është i mpirë, n p b → a → → dhe b → janë në drejtime të kundërta. Në një situatë pinguliteti a → dhe b →, dhe a → është zero, projeksioni i a → në drejtimin b → është vektori zero.

Karakteristika numerike e projeksionit të një vektori në një bosht është projeksioni numerik i një vektori në një bosht të caktuar.

Përkufizimi 2

Projeksioni numerik i vektorit mbi boshtështë një numër që është i barabartë me prodhimin e gjatësisë së një vektori të caktuar dhe kosinusit të këndit ndërmjet vektorit të dhënë dhe vektorit që përcakton drejtimin e boshtit.

Projeksioni numerik i A B → në L shënohet n p L A B → , dhe a → në b → - n p b → a → .

Bazuar në formulën, marrim n p b → a → = a → · cos a → , b → ^ , nga ku a → është gjatësia e vektorit a → , a ⇀ , b → ^ është këndi ndërmjet vektorëve a → dhe b → .

Marrim formulën për llogaritjen e projeksionit numerik: n p b → a → = a → · cos a → , b → ^ . Është i zbatueshëm për gjatësitë e njohura a → dhe b → dhe këndin ndërmjet tyre. Formula është e zbatueshme për koordinatat e njohura a → dhe b →, por ekziston një formë e thjeshtuar.

Shembulli 2

Gjeni projeksionin numerik të a → në një vijë të drejtë në drejtimin b → me gjatësi a → të barabartë me 8 dhe një kënd midis tyre 60 gradë. Me kusht kemi një ⇀ = 8, a ⇀, b → ^ = 60 °. Pra, le të zëvendësojmë vlerat numerike në formulën n p b ⇀ a → = a → · cos a → , b → ^ = 8 · cos 60 ° = 8 · 1 2 = 4 .

Përgjigje: 4.

Me cos të njohur (a → , b → ^) = a ⇀ , b → a → · b → , kemi a → , b → si prodhim skalar të a → dhe b → . Duke ndjekur formulën n p b → a → = a → · cos a ⇀ , b → ^ , mund të gjejmë projeksionin numerik a → të drejtuar përgjatë vektorit b → dhe të marrim n p b → a → = a → , b → b → . Formula është ekuivalente me përkufizimin e dhënë në fillim të paragrafit.

Përkufizimi 3

Projeksioni numerik i vektorit a → mbi një bosht që përkon në drejtim me b → është raporti i prodhimit skalar të vektorëve a → dhe b → me gjatësinë b → . Formula n p b → a → = a → , b → b → është e zbatueshme për të gjetur projeksionin numerik të a → në një vijë që përkon në drejtim me b → , me koordinata të njohura a → dhe b →.

Shembulli 3

Jepet b → = (- 3 , 4) . Gjeni projeksionin numerik a → = (1, 7) në L.

Zgjidhje

Në planin koordinativ n p b → a → = a → , b → b → ka formën n p b → a → = a → , b → b → = a x b x + a y b y b x 2 + b y 2 , me a → = (a x , a y ) dhe b → = b x, b y. Për të gjetur projeksionin numerik të vektorit a → në boshtin L, ju nevojiten: n p L a → = n p b → a → = a → , b → b → = a x · b x + a y · b y b x 2 + b y 2 = 1 · (- 3) + 7 · 4 (- 3) 2 + 4 2 = 5.

Përgjigje: 5.

Shembulli 4

Gjeni projeksionin e a → në L, që përkon me drejtimin b →, ku ka a → = - 2, 3, 1 dhe b → = (3, - 2, 6). Hapësira tre-dimensionale është e specifikuar.

Zgjidhje

Duke pasur parasysh a → = a x , a y , a z dhe b → = b x , b y , b z , ne llogarisim prodhimin skalar: a ⇀ , b → = a x · b x + a y · b y + a z · b z . Gjatësia b → gjendet duke përdorur formulën b → = b x 2 + b y 2 + b z 2 . Nga kjo rrjedh se formula për përcaktimin e projeksionit numerik a → do të jetë: n p b → a ⇀ = a → , b → b → = a x · b x + a y · b y + a z · b z b x 2 + b y 2 + b z 2 .

Zëvendësoni vlerat numerike: n p L a → = n p b → a → = (- 2) 3 + 3 (- 2) + 1 6 3 2 + (- 2) 2 + 6 2 = - 6 49 = - 6 7 .

Përgjigje: - 6 7.

Le të shohim lidhjen midis a → në L dhe gjatësisë së projeksionit a → në L. Le të vizatojmë një bosht L, duke shtuar një → dhe b → nga një pikë në L, pas së cilës vizatojmë një vijë pingule nga fundi a → në L dhe vizatojmë një projeksion në L. Ekzistojnë 5 variacione të imazhit:

Së pari rasti me a → = n p b → a → → do të thotë a → = n p b → a → → , pra n p b → a → = a → · cos (a , → b → ^) = a → · cos 0 ° = a → = n p b → a → → .

Së dyti rasti nënkupton përdorimin e n p b → a → ⇀ = a → · cos a → , b → , që do të thotë n p b → a → = a → · cos (a → , b →) ^ = n p b → a → → .

Së treti rasti shpjegon se kur n p b → a → → = 0 → marrim n p b ⇀ a → = a → · cos (a → , b → ^) = a → · cos 90 ° = 0 , atëherë n p b → a → → = 0 dhe n p b → a → = 0 = n p b → a → → .

Së katërti rasti tregon n p b → a → → = a → · cos (180 ° - a → , b → ^) = - a → · cos (a → , b → ^) , vijon n p b → a → = a → · cos ( a → , b → ^) = - n p b → a → → .

E pesta rasti tregon a → = n p b → a → → , që do të thotë a → = n p b → a → → , pra kemi n p b → a → = a → · cos a → , b → ^ = a → · cos 180° = - a → = - n p b → a → .

Përkufizimi 4

Projeksioni numerik i vektorit a → në boshtin L, i cili drejtohet në të njëjtën mënyrë si b →, ka vlerën e mëposhtme:

gjatësia e projeksionit të vektorit a → në L, me kusht që këndi ndërmjet a → dhe b → të jetë më i vogël se 90 gradë ose i barabartë me 0: n p b → a → = n p b → a → → me kushtin 0 ≤ (a → , b →) ^< 90 ° ;
zero me kusht që a → dhe b → të jenë pingul: n p b → a → = 0, kur (a → , b → ^) = 90 °;
gjatësia e projeksionit a → në L, shumëzuar me -1, kur ka një kënd të mpirë ose të drejtë të vektorëve a → dhe b →: n p b → a → = - n p b → a → → me kushtin 90 °< a → , b → ^ ≤ 180 ° .

Shembulli 5

Jepet gjatësia e projeksionit a → në L, e barabartë me 2. Gjeni projeksionin numerik a → me kusht që këndi të jetë 5 π 6 radian.

Zgjidhje

Nga kushti del qartë se ky kënd është i mpirë: π 2< 5 π 6 < π . Тогда можем найти числовую проекцию a → на L: n p L a → = - n p L a → → = - 2 .

Përgjigje: - 2.

Shembulli 6

Jepet një rrafsh O x y z me gjatësi vektoriale a → e barabartë me 6 3, b → (- 2, 1, 2) me kënd 30 gradë. Gjeni koordinatat e projeksionit a → në boshtin L.

Zgjidhje

Së pari, ne llogarisim projeksionin numerik të vektorit a →: n p L a → = n p b → a → = a → · cos (a → , b →) ^ = 6 3 · cos 30 ° = 6 3 · 3 2 = 9 .

Sipas kushtit, këndi është akut, atëherë projeksioni numerik a → = gjatësia e projeksionit të vektorit a →: n p L a → = n p L a → → = 9. Ky rast tregon se vektorët n p L a → → dhe b → janë të bashkëdrejtuar, që do të thotë se ekziston një numër t për të cilin barazia është e vërtetë: n p L a → → = t · b → . Nga këtu shohim se n p L a → → = t · b → , që do të thotë se mund të gjejmë vlerën e parametrit t: t = n p L a → → b → = 9 (- 2) 2 + 1 2 + 2 2 = 9 9 = 3 .

Pastaj n p L a → → = 3 · b → me koordinatat e projeksionit të vektorit a → në boshtin L të barabartë me b → = (- 2, 1, 2), ku është e nevojshme të shumëzohen vlerat me 3. Kemi n p L a → → = (- 6 , 3 , 6) . Përgjigje: (- 6, 3, 6).

Është e nevojshme të përsëriten informacionet e mësuara më parë për gjendjen e kolinearitetit të vektorëve.

Nëse vëreni një gabim në tekst, ju lutemi theksoni atë dhe shtypni Ctrl+Enter

Projeksioni algjebrik i një vektori në çdo bosht është i barabartë me produktin e gjatësisë së vektorit dhe kosinusit të këndit midis boshtit dhe vektorit:

Pr a b = |b|cos(a,b) ose

Ku a b është prodhimi skalar i vektorëve, |a| - moduli i vektorit a.

Udhëzimet. Për të gjetur projeksionin e vektorit Pr a b në linjë, duhet të specifikoni koordinatat e vektorëve a dhe b. Në këtë rast, vektori mund të specifikohet në plan (dy koordinata) dhe në hapësirë (tre koordinata). Zgjidhja që rezulton ruhet në një skedar Word. Nëse vektorët specifikohen përmes koordinatave të pikave, atëherë duhet të përdorni këtë kalkulator.

Klasifikimi i projeksioneve vektoriale

Llojet e projeksioneve sipas përkufizimit projeksion vektorial

Projeksioni gjeometrik i vektorit AB në boshtin (vektorin) quhet vektor A"B", fillimi i të cilit A' është projeksioni i fillimit A në bosht (vektor), dhe fundi B' është projeksion. të skajit B në të njëjtin bosht.
Projeksioni algjebrik i vektorit AB në boshtin (vektorin) quhet gjatësia e vektorit A"B", marrë me shenjën + ose -, në varësi të faktit nëse vektori A"B" ka të njëjtin drejtim me boshtin ( vektor).

Llojet e projeksioneve sipas sistemit të koordinatave

Vetitë e projeksionit të vektorit

Projeksioni gjeometrik i një vektori është një vektor (ka një drejtim).
Projeksioni algjebrik i një vektori është një numër.

Teoremat e projeksionit të vektorit

Teorema 1. Projeksioni i shumës së vektorëve në çdo bosht është i barabartë me projeksionin e mbledhjeve të vektorëve në të njëjtin bosht.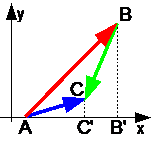

AC" =AB" +B"C"

Teorema 2. Projeksioni algjebrik i një vektori në çdo bosht është i barabartë me produktin e gjatësisë së vektorit dhe kosinusit të këndit midis boshtit dhe vektorit:

Pr a b = |b|·cos(a,b)

Llojet e projeksioneve vektoriale

projeksioni në boshtin OX.
projeksioni në boshtin OY.
projeksioni në një vektor.

Projeksioni në boshtin OX	Projeksioni në boshtin OY	Projeksion në vektor
Nëse drejtimi i vektorit A’B’ përkon me drejtimin e boshtit OX, atëherë projeksioni i vektorit A’B’ ka një shenjë pozitive.	Nëse drejtimi i vektorit A’B’ përkon me drejtimin e boshtit OY, atëherë projeksioni i vektorit A’B’ ka një shenjë pozitive.	Nëse drejtimi i vektorit A'B' përkon me drejtimin e vektorit NM, atëherë projeksioni i vektorit A'B' ka një shenjë pozitive.
Nëse drejtimi i vektorit është i kundërt me drejtimin e boshtit OX, atëherë projeksioni i vektorit A’B’ ka shenjë negative.	Nëse drejtimi i vektorit A’B’ është i kundërt me drejtimin e boshtit OY, atëherë projeksioni i vektorit A’B’ ka një shenjë negative.	Nëse drejtimi i vektorit A'B' është i kundërt me drejtimin e vektorit NM, atëherë projeksioni i vektorit A'B' ka një shenjë negative.
Nëse vektori AB është paralel me boshtin OX, atëherë projeksioni i vektorit A'B' është i barabartë me vlerën absolute të vektorit AB.	Nëse vektori AB është paralel me boshtin OY, atëherë projeksioni i vektorit A'B' është i barabartë me vlerën absolute të vektorit AB.	Nëse vektori AB është paralel me vektorin NM, atëherë projeksioni i vektorit A'B' është i barabartë me vlerën absolute të vektorit AB.
Nëse vektori AB është pingul me boshtin OX, atëherë projeksioni A'B' është i barabartë me zero (vektor zero).	Nëse vektori AB është pingul me boshtin OY, atëherë projeksioni A'B' është i barabartë me zero (vektor zero).	Nëse vektori AB është pingul me vektorin NM, atëherë projeksioni A'B' është i barabartë me zero (vektor zero).

1. Pyetje: A mundet projeksioni i një vektori të ketë shenjë negative? Përgjigje: Po, vektori i projeksionit mund të jetë një vlerë negative. Në këtë rast, vektori ka drejtim të kundërt (shiko se si janë drejtuar boshti OX dhe vektori AB)
2. Pyetje: A mund të përputhet projeksioni i një vektori me vlerën absolute të vektorit? Përgjigje: Po, mundet. Në këtë rast, vektorët janë paralelë (ose shtrihen në të njëjtën linjë).
3. Pyetje: A mund të jetë projeksioni i një vektori të barabartë me zero (vektor null). Përgjigje: Po, mundet. Në këtë rast, vektori është pingul me boshtin (vektorin) përkatës.

Shembulli 1. Vektori (Fig. 1) formon një kënd prej 60° me boshtin OX (ai specifikohet nga vektori a). Nëse OE është një njësi shkallë, atëherë |b|=4, pra .

Në të vërtetë, gjatësia e vektorit ( projeksioni gjeometrik b) është e barabartë me 2, dhe drejtimi përkon me drejtimin e boshtit OX.

Shembulli 2. Vektori (Fig. 2) formon një kënd (a,b) = 120 o me boshtin OX (me vektorin a). Gjatësia |b| vektori b është i barabartë me 4, pra pr a b=4·cos120 o = -2.

Në të vërtetë, gjatësia e vektorit është 2, dhe drejtimi është i kundërt me drejtimin e boshtit.

Projeksioni vektori mbi një bosht është një vektor që përftohet duke shumëzuar projeksionin skalar të një vektori mbi këtë bosht dhe vektorin njësi të këtij boshti. Për shembull, nëse një x - projeksion skalar vektoriale A në boshtin X, pastaj një x i- projeksioni i tij vektorial mbi këtë bosht.

Le të shënojmë projeksion vektorial njëjtë si vetë vektori, por me indeksin e boshtit në të cilin projektohet vektori. Pra, projeksioni vektorial i vektorit A në boshtin X që shënojmë A x ( yndyrë një shkronjë që tregon një vektor dhe një nënshkrim të emrit të boshtit) ose (një shkronjë jo e trashë që tregon një vektor, por me një shigjetë në krye (!) dhe një nënshkrim të emrit të boshtit).

Projeksion skalar vektor për bosht quhet numri, vlera absolute e së cilës është e barabartë me gjatësinë e segmentit të boshtit (në shkallën e zgjedhur) të mbyllur midis projeksioneve të pikës fillestare dhe pikës së fundit të vektorit. Zakonisht në vend të shprehjes projeksion skalar ata thjesht thonë - projeksioni. Projeksioni shënohet me të njëjtën shkronjë si vektori i projektuar (në shkrimin normal, jo të trashë), me një indeks më të ulët (si rregull) të emrit të boshtit në të cilin projektohet ky vektor. Për shembull, nëse një vektor projektohet në boshtin X A, atëherë projeksioni i tij shënohet me x. Kur projektohet i njëjti vektor në një bosht tjetër, nëse boshti është Y, projeksioni i tij do të shënohet me y.

Për të llogaritur projeksionin vektoriale në një bosht (për shembull, boshti X), është e nevojshme të zbritet koordinata e pikës së fillimit nga koordinata e pikës fundore të saj, d.m.th.
a x = x k − x n.
Projeksioni i një vektori në një bosht është një numër. Për më tepër, projeksioni mund të jetë pozitiv nëse vlera x k është më e madhe se vlera x n,

negative nëse vlera x k është më e vogël se vlera x n

dhe e barabartë me zero nëse x k është e barabartë me x n.

Projeksioni i një vektori mbi një bosht mund të gjendet gjithashtu duke ditur modulin e vektorit dhe këndin që ai bën me këtë bosht.

Nga figura është e qartë se a x = a Cos α

domethënë, projeksioni i vektorit në bosht është i barabartë me produktin e modulit të vektorit dhe kosinusit të këndit ndërmjet drejtimit të boshtit dhe drejtimi i vektorit. Nëse këndi është akut, atëherë
Cos α > 0 dhe a x > 0, dhe, nëse është i mpirë, atëherë kosinusi i këndit të mpirë është negativ, dhe projeksioni i vektorit mbi boshtin gjithashtu do të jetë negativ.

Këndet e matura nga boshti në drejtim të kundërt të akrepave të orës konsiderohen pozitive, dhe këndet e matura përgjatë boshtit janë negative. Megjithatë, meqenëse kosinusi është një funksion çift, domethënë Cos α = Cos (− α), kur llogariten projeksionet, këndet mund të numërohen si në drejtim të akrepave të orës ashtu edhe në të kundërt.

Për të gjetur projeksionin e një vektori në një bosht, moduli i këtij vektori duhet të shumëzohet me kosinusin e këndit midis drejtimit të boshtit dhe drejtimit të vektorit.

Koordinatat vektoriale— koeficientët e kombinimit të vetëm linear të mundshëm të vektorëve bazë në sistemin e zgjedhur koordinativ, të barabartë me vektorin e dhënë.

ku janë koordinatat e vektorit.

Produkt skalar vektorët

Produkt skalar i vektorëve[- në dimensione të fundme hapësirë vektoriale përkufizohet si shuma e produkteve të përbërësve identikë që shumëzohen vektorët.

Për shembull, S.p.v. a = (a 1 , ..., a n) Dhe b = (b 1 , ..., b n):

(a , b ) = a 1 b 1 + a 2 b 2 + ... + a n b n