Mësimi praktik “llogaritja e derivateve”. Mësimi praktik “llogaritja e derivateve” Gjeni derivatin e funksionit y
Objektivat e mësimit:
arsimore- të njohë formulat e diferencimit; rregullat e diferencimit;
diferencimi i një funksioni kompleks; kuptimi fizik dhe gjeometrik i derivatit;
ekuacioni i tangjentes me grafikun e një funksioni.
Zhvillimore - të jetë në gjendje të gjejë derivatet e funksioneve; zgjidh probleme duke përdorur kuptimin fizik, kuptimin gjeometrik; të gjejë vlerën e derivatit të një funksioni në një pikë; të shpjegojë dhe të arsyetojë saktë në mënyrë matematikore veprimet e kryera.
arsimore - kultivojnë pavarësinë, përgjegjësinë, reflektimin.
Gjatë orëve të mësimit
I. Momenti organizativ.
II. Kontrollimi i detyrave të shtëpisë
(gjatë pushimeve, konsulentët kontrollojnë (studentët) dhe caktojnë notat).
III. Vendosja e qëllimeve dhe motivimi
Mësuesi/ja informon nxënësit se kjo orë është ora përfundimtare me temën “Llogaritja e derivateve” dhe i fton ata të formulojnë qëllimet e tyre.
Mësuesi: "Filozofi i madh Konfuci dikur tha: "Tri rrugë të çojnë në njohuri: rruga e reflektimit është rruga më fisnike, rruga e imitimit është rruga më e lehtë dhe rruga e përvojës është rruga më e hidhur". Kështu që sot në klasë, secili prej jush do të përcaktojë se në cilën rrugë drejt njohjes së kësaj teme është.”
Nxënësve u jepet detyrë të demonstrojnë njohuritë dhe aftësitë e tyre në llogaritjen e derivateve dhe u jepet një plan mësimi.
Faza I: Përfundimi i detyrës duke përdorur kartën "Kujto".
(testimi i njohurive të formulave dhe rregullave të diferencimit).
Faza II: Punë ballore gojore për përsëritjen dhe përgjithësimin e njohurive.
Faza III:"Parashikimi i testit" (kur kryeni këtë detyrë, ndihma e konsulentëve është e pranueshme).
IFaza V: Zgjidhja e një problemi praktik.
Faza V: Punë e pavarur
Vlerësohen fazat I, III, V të punës dhe të detyrave të shtëpisë. Konsulentët kontrollojnë dhe futin rezultatet në tabelën e vlerësimit.
Kriteret e vlerësimit: "5"- 19-20 pikë;
"4"- 15-18 pikë;
"3"- 10-14 pikë.
Rrugët drejt dijes
- Riprodhimi dhe korrigjimi i njohurive referuese
Faza I.
Synimi: kontrolli, vetëkontrolli i njohjes së formulave dhe rregullave të diferencimit
Mbani mend! F.I. _________________________________________________ |
|
Derivat |
|
c,c - kundër t |
|
|
|
|
|
f"(x)+ g"(x) |
|
f(x)* g(x) |
|
|
|
Në përfundim të kësaj detyre, kryhet një vetë-test duke përdorur "Tabela e derivateve". Kartat u dorëzohen konsulentëve për verifikim (korrigjimet në karta nuk lejohen).
V. Përgjithësimi dhe sistematizimi i njohurive
Faza II.
1. Punë ballore gojore.
A. Krijo një detyrë për këtë gjendje dhe zgjidhe atë.
![]()
1. Gjeni vlerën e derivatit të funksionit në pikën t = 3. (Përgjigje: 21.)
2. Krijo një ekuacion për tangjenten në grafikun e funksionit në pikën t = 3. (Përgjigje: y = 21x-45.).
3. Gjeni shpejtësinë e trupit dhe nxitimin në momentin t=3c, nëse ligji i lëvizjes jepet me formulën. (Përgjigje: 21 m/s, 16 m/s²).
4. Gjeni koeficientin këndor të tangjentes së tërhequr në grafikun e funksionit në pikën t = 3. (Përgjigje: 21.).
5. Gjeni tangjenten e këndit të prirjes së tangjentes me grafikun e funksionit në pikën t = 3 dhe përcaktoni llojin e këndit ndërmjet tangjentes dhe drejtimit pozitiv të boshtit Ox. (Përgjigje: tgα, këndi α është i mprehtë)
B. Gjeni derivatet e funksioneve

2. Faza III"Parashikimi i testit"


Në përfundim të kësaj detyre bëhet një autotest mbi bazën e përgjigjeve përfundimtare dhe testet u dorëzohen konsulentëve. (Korrigjimet në karta nuk lejohen).
Përgjigjet:
1 opsion |
||||
Opsioni 2 |
- Zgjidhja e problemit
IFaza V
Zgjidhja frontale e një problemi të nivelit të avancuar (zgjidhja kryhet nga konsulentët së bashku me klasën).
Detyrë
Në cilat vlera parametrash a tangjentet me grafikun e një funksioni ![]()
të vizatuara në pikat e kryqëzimit të tij me boshtin X, formojnë një kënd prej 60° ndërmjet tyre?

Grafiku është një parabolë me degë lart që kryqëzojnë boshtin X në dy pika (rasti a=0 nuk e plotëson kuptimin e problemit):
IX. Përmbledhja dhe notimi
1. Pyetje: a) A është arritur qëllimi i orës së mësimit?
b) Cila fazë dukej më e vështira?
c) Cila ishte më interesante?
2. Konsulentët shpallin rezultatet (numrin dhe emrat e studentëve në rrugë
imitimi, mënyrat e reflektimit dhe mënyrat e përvojës).
Punë praktike
matematikë
1. Gjetja e kufirit të një funksioni. E para dhe e dyta janë kufij të mrekullueshëm.
2. Derivat i një funksioni kompleks. Studimi i një funksioni të një ndryshoreje dhe vizatimi i grafikëve.
3. Testi “Zbatimi i llogaritjes diferenciale në studimin e funksioneve”.
4. Gjetja e integraleve të pacaktuar. Llogaritja e integraleve të caktuar.
5. Llogaritja e përcaktorëve.
6. Zgjidhja e sistemeve të ekuacioneve lineare duke përdorur metodën Cramer. Test.
7. Zgjidhja e problemave me temën “Komplete”. Formulat e algjebrës logjike.
8. Llogaritja e probabiliteteve të ngjarjeve të rastësishme. Formula e probabilitetit total.
9. Llogaritja e karakteristikave numerike.
10. Testi “Bazat e teorisë së probabilitetit dhe statistikat matematikore”
11. Forma trigonometrike e një numri kompleks.
12. Veprimet me numra kompleks në forma të ndryshme.
UDHËZIME METODOLOGJIKE PËR PUNË PRAKTIKE NË MATEMATIKË
KURSI 2
Një mësim praktik është një formë e organizimit të procesit arsimor, i cili përfshin studentët që kryejnë një ose më shumë punë praktike me detyrë dhe nën drejtimin e një mësuesi.
Kështu, në orët praktike të matematikës, nxënësve u zhvillohet aftësia për zgjidhjen e problemave, të cilat në të ardhmen duhet të përdoren për zgjidhjen e problemeve profesionale në disiplina të veçanta.
Gjatë punës praktike, studentët zotërojnë aftësinë për të përdorur burime informacioni, të punojnë me dokumente rregullatore dhe materiale udhëzuese, libra referimi, të bëjnë vizatime, diagrame, tabela, të zgjidhin lloje të ndryshme problemesh dhe të bëjnë llogaritjet.
Problemet që zgjidhen gjatë mësimeve praktike në matematikë:
1) zgjerimi dhe konsolidimi i njohurive teorike në matematikë të marra gjatë ligjëratave;
2) zhvillimi i aftësive praktike dhe aftësive të nevojshme për zgjidhjen e suksesshme të problemeve në matematikë tek studentët;
3) zhvillimi i nevojës së nxënësve për vetë-edukim dhe përmirësimin e njohurive dhe aftësive në procesin e studimit të matematikës;
4) formimi i një qëndrimi krijues dhe një qasje kërkimore në procesin e studimit të matematikës;
5) formimi i cilësive të rëndësishme profesionale të një specialisti të ardhshëm dhe aftësive në zbatimin e njohurive të fituara në fushën profesionale.
Mësimi praktik nr. 1. Llogaritja e kufijve të funksionit. E para dhe e dyta janë kufij të mrekullueshëm.
Subjekti : Llogaritja e kufijve të funksionit.
Synimi: përvetësimi i njohurive bazë në fushën e degëve themelore të matematikës . Testimi i asimilimit të njohurive për llogaritjen e kufijve të funksioneve. Përsëritni dhe sistematizoni njohuritë për këtë temë.
Detyrat:
Zhvillimi i të menduarit kreativ profesional;
Zotërimi i gjuhës së shkencës, aftësitë e koncepteve operative;
Zotërimi i aftësive të vendosjes dhe zgjidhjes së problemeve;
Thellimi i trajnimit teorik dhe praktik;
Zhvillimi i iniciativës dhe pavarësisë së nxënësve.
Forcimi i aftësive kompjuterike;
Vazhdoni të punoni në fjalimin matematikor.
Formimi i aftësive për punë të pavarur, punë me tekst shkollor, aftësi për përvetësim të pavarur të njohurive;
Zhvillimi i aftësisë për të nxjerrë në pah gjënë kryesore kur punoni me tekst;
Formimi i të menduarit të pavarur, operacionet mendore: krahasimi, analiza, sinteza, përgjithësimi, analogjia;
Tregoju nxënësve rolin e punës sistematike për thellimin dhe rritjen e forcës së njohurive, mbi kulturën e kryerjes së detyrave;
Zhvillimi i aftësive krijuese të nxënësve.
Ofrimi i punës praktike:
Materiali teorik i rekomandimeve metodologjike për punë praktike.
Matematikë, – Seria: Arsimi i mesëm profesional. - Rostov-on-Don “Phoenix”, f.
Ecuria e mësimit praktik.
1.Formulimi i temës së mësimit, shpjegimi i lidhjes së temës me temat e tjera të disiplinës akademike;
2.Kontrollimi i gatishmërisë së nxënësve për mësim;
3. Zhvillimi i mësimit aktual sipas temës dhe në përputhje me programin e punës të disiplinës:
Studioni materialin teorik me temën "Llogaritja e kufijve të funksioneve".
Konsideroni shembuj të zgjidhjes së detyrave tipike.
Bëni punë të pavarur për llogaritjen e kufijve të funksioneve duke përdorur kufijtë e parë dhe të dytë të shquar.
Përgjigjuni pyetjeve të sigurisë.
Informacion teorik dhe rekomandime metodologjike
mbi zgjidhjen e problemeve.
1. Prezantimi i materialit teorik.
Për të llogaritur kufirin e një funksioni në një pikë, duhet:
1) Zëvendësoni në vend të ndryshores x çfarë priret x.
2) Nëse pas përfundimit të hapit 1) marrim një pasiguri të formularit https://pandia.ru/text/78/405/images/image003_6.png" width="19" height="22 src=">dhe zëvendësojmë shigjeta me minus: (x-a).
3) Nëse, pas përfundimit të hapit 1), marrim një pasiguri të formularit https://pandia.ru/text/78/405/images/image002_13.png" width="18" height="31 src="> lidhur me vlerat e funksioneve trigonometrike, duhet të përdorim kufirin e parë të shquar.
Përkufizimi. Kufiri i parë i shquar quhet limit
https://pandia.ru/text/78/405/images/image007_4.png" alt="$\displaystyle \lim_(x\to0)\dfrac(\sin x)(x)=1. $" width="102" height="52">!}
5) Përkufizimi:Kufiri i dytë i shquar i quajtur limit

Numri i dhënë nga ky kufi luan një rol shumë të rëndësishëm si në analizën matematikore ashtu edhe në degët e tjera të matematikës. Numri thirret baza e logaritmeve natyrore ( https://pandia.ru/text/78/405/images/image009_4.png" alt="$ e$" width="11" height="14">показывает, что -- иррациональное число, несколько первых десятичных знаков которого таковы:!}
![]()
2. Konsolidimi i materialit të studiuar.
Shembulli 1
https://pandia.ru/text/78/405/images/image015_1.png" width="28" height="30 src=">= -4
Ne përdorëm rregullin 1) dhe zëvendësuam në vend të x atë për të cilën x duhet të përpiqet, d.m.th. x=2.
Shembulli 2
https://pandia.ru/text/78/405/images/image017_1.png" width="154" height="32 src=">.png" width="21" height="30 src=">= 5
Shembulli 3
https://pandia.ru/text/78/405/images/image021_1.png" width="199" height="37 src=">.png" width="137" height="35 src=">. png" width="138" height="24 src=">=3+3=6
Shembulli 4
https://pandia.ru/text/78/405/images/image004_7.png" width="22" height="31 src=">.png" width="104" height="46 src=">. png" height="30 src=">
Shembulli 5
https://pandia.ru/text/78/405/images/image032_0.png" width="61" height="46 src=">.png" height="30 src=">=2
Shembulli 6
https://pandia.ru/text/78/405/images/image036_0.png" width="18" height="28 src=">
b) 
V) 
3. Konsolidimi i njohurive, aftësive dhe aftësive.
Bëni punë të pavarur për llogaritjen e kufijve të funksioneve.
Puna praktike nr.1. opsioni 1 Llogaritni kufirin e funksionit: 1. 2. 3. 10. | Puna praktike nr.1. Opsioni 2 Llogaritni kufirin e funksionit: 1. 2. 3. 10. |
Puna praktike nr.2.
Subjekti : Gjetja e derivatit të një funksioni. Studimi i funksionit të një ndryshoreje dhe vizatimi i grafikut.
Synimi : Provoni në praktikë njohuritë për konceptin e një derivati të një funksioni, aftësinë për të gjetur derivatet e funksioneve elementare, funksionet komplekse, funksionet e anasjellta, duke përdorur tabelën e derivateve dhe rregullat e diferencimit, konceptin e një funksioni kompleks dhe të anasjelltë, aftësinë. për të përdorur një derivat për të studiuar funksionet.
Ofrimi i punës praktike:
Libër mësuesi. "Matematika". - M.: Bustard, 2010.
Matematika. M: Forum-Infa 2008.
Karta individuale me opsion pune praktike.
1. Materiali teorik dhe shembuj të gjetjes së derivatit të një funksioni.
Përkufizimi: Derivati i funksionit f(x) (f"(x)) në pikën x është kufiri i raportit të rritjes së funksionit me rritjen e argumentit kur rritja e argumentit tenton në zero:
https://pandia.ru/text/78/405/images/image061_0.png" width="209 height=235" height="235">
Rregullat e diferencimit.
Nëse funksionet f(x) dhe g(x) kanë derivate, atëherë
2. (u+v)′=u′+v′
3. (uv)′=u′v+v′u
4. (C u)′=C u′, ku C=konst
5..png" width="49" height="54 src=">
6. Derivati i një funksioni kompleks:
f′(g(x))=f′(g) g′(x)
2. Shembuj.
1..png" width="61" height="41 src=">.png" width="20" height="41 src=">.png" width="20" height="41 src="> .png" width="69" height="41 src=">+4).
Funksioni është produkt i dy faktorëve: u=https://pandia.ru/text/78/405/images/image071_0.png" width="72" height="41 src=">.png" width=" 64" height="41 src=">.png" width="19" height="41 src=">.png" width="45" height="51 src=">.
Funksioni është herësi i dy shprehjeve: u=https://pandia.ru/text/78/405/images/image079.png" width="52" height="41 src=">..png" width= "215" " height="57 src=">.png" width="197 height=36" height="36">
Zgjidhje. Le të gjejmë derivatin e këtij funksioni duke përdorur rregullin e diferencimit të funksioneve komplekse (formula 6):

5. Nëse , atëherë 
6. y = x 3 – 3x 2 + 5x+ 2. Le të gjejmë y "(–1).
y " = 3x 2 – 6x+ 5. Prandaj, y "(–1) = 14.
7. Nëse y= log x cos x, Kjo y" = (ln x)"cos x+ln x(cos x) " =1/x∙cos x-ln x mëkat x.
Le të jepet një funksion. Për ta studiuar atë ju duhet:
1) Gjeni domenin e tij të përkufizimit. Nëse nuk është shumë e vështirë, është e dobishme të gjesh edhe gamën. (Megjithatë, në shumë raste, çështja e gjetjes shtyhet derisa të gjenden ekstremet e funksionit.)
2) Zbuloni vetitë e përgjithshme të funksionit që do të ndihmojnë në përcaktimin e sjelljes së tij: nëse funksioni është çift apo tek, nëse është periodik.
3) Zbuloni se si sillet funksioni kur argumenti u afrohet pikave kufitare të fushës së përkufizimit, nëse ka pika të tilla kufitare. Nëse një funksion ka pika ndërprerjeje, atëherë këto pika duhet të kontrollohen edhe për praninë e asimptotave vertikale të funksionit. Gjeni asimptota të zhdrejta.
4) Gjeni pikat e kryqëzimit të grafikut me boshtet e koordinatave, i cili konsiston thjesht në llogaritjen e vlerës së funksionit nën kushtin:
Me bosht OX: y=0;
Me bosht OY: x=0.
Gjetja e pikave të kryqëzimit me boshtin mund të çojë në nevojën për të zgjidhur një ekuacion kompleks algjebrik, i cili, ndoshta, mund të bëhet vetëm përafërsisht. Pasi të kemi gjetur rrënjët e funksionit dhe pikat e ndërprerjes, mund të përcaktojmë shenjën e funksionit në secilën prej intervaleve midis këtyre pikave. Kjo mund të bëhet ose duke llogaritur vlerën e funksionit në çdo pikë të intervalit, ose duke përdorur metodën e intervalit.
5) Gjeni intervalet e monotonitetit. Për ta bërë këtë, gjeni derivatin dhe zgjidhni pabarazinë:
https://pandia.ru/text/78/405/images/image089.png" width="49" height="19 src=">, funksioni po zvogëlohet.
Pasi të kemi gjetur intervalet e monotonitetit, mund të përcaktojmë menjëherë pikat e ekstremumit lokal: ku një rritje zëvendësohet me një ulje, vendosen maksimumet lokale, dhe ku një ulje zëvendësohet me një rritje, vendosen minimumet lokale.
6) Gjetja e intervaleve të konveksitetit dhe konkavitetit kryhet duke përdorur derivatin e dytë..png" width="39" height="19 src="> në intervalet:
nëse https://pandia.ru/text/78/405/images/image090.png" width="39" height="19 src=">‹0, atëherë kurba e grafikut të funksionit është konveks.
Në të njëjtën kohë, ne përcaktojmë pikat e përkuljes si ato pika në të cilat funksioni ndryshon drejtimin e konveksitetit (dhe është i vazhdueshëm).
7) Gjetja e pikave të prerjes së grafikut me asimptotën dhe pikat shtesë. Kjo pikë nuk është e detyrueshme, por gjetja e pikave të tilla e bën të plotë dhe të plotë studimin e funksionit dhe grafikun e tij.
Vini re se është e dobishme që menjëherë të vizatohen pikat në boshtet e koordinatave dhe në grafikun që merren gjatë studimit të funksioneve në vizatim. Kjo ndihmon për të kuptuar pamjen e grafikut gjatë rrugës.
3. Bëjeni vetë:
|
opsion | Gjeni derivatin e funksionit y: |
opsion | Gjeni derivatin e funksionit y: |
1.y=6- | 1. y=-6- 5.y= |
||
1. y=-7-1 | 1. y=-7-1 |
||
1.y=4x-3tgx+6x-8 | 1.y=-5x+2ctgx+3x-2 |
||
Mësim praktik
Tema: Gjetja e derivateve. Zbatimi i derivatit në studimin e funksioneve dhe vizatimin e grafikëve.
Synimi: Zotëroni llogaritjen e derivateve, mësoni të eksploroni një funksion duke përdorur derivatin
Mjetet e edukimit: fletore për ushtrime praktike, prezantime mbi temën, burimet e internetit.
1. Shqyrtoni materialin teorik me temat: “Rregullat për llogaritjen e derivateve”, “Ekstremi i një funksioni”, “Konveksiteti, konkaviteti. Pika e përkuljes."
2. Rishikoni mostrat e detyrave.
3. Plotësoni detyrën testuese nr. 1.
Pyetjet e kontrollit:
1. Përcaktoni maksimumin (minimumin) e një funksioni në një pikë. Çfarë mund të thuhet për shenjën e rritjes së funksionit në një lagje mjaft të vogël të pikës maksimale (minimale)?
2. Cilat janë kushtet e nevojshme për ekzistimin e një ekstremi të një funksioni? Cili është kuptimi i tyre gjeometrik?
3. Cili është rregulli për gjetjen e vlerave më të mëdha dhe më të vogla të një funksioni në një segment?
4. Përcaktoni konveksitetin (konkavitetin) e një lakore në një interval.
5. Cili është rregulli për gjetjen e intervaleve të konveksitetit dhe konkavitetit të një lakore?
6. Pika e lakimit të lakores. Si ta gjeni atë?
7. Cili është algoritmi për ndërtimin e grafikut të një funksioni?
Rregullat për llogaritjen e derivateve
Derivat i një funksioni kompleks.
Nëse në=ƒ( Dhe), u=φ(x), atëherë në¢ ( X)=ƒ¢ (i)·φ¢ (X).
Derivat i një shume.
Nëse në(X)=Dhe(X)+v (X), Kjo në¢ (X)=Dhe¢ (X)+v ¢ (X)
Derivat i produktit.
Nëse y(x)=u(X)· v (X), Kjo në¢ = Dhe¢ · v + u · v ¢ .
Veçanërisht, ( Me· Dhe)¢ =c· Dhe¢, pra faktori konstant nxirret nga nën shenjën derivatore. Është e lehtë ta verifikosh këtë
(u 2 ) ¢ = 2 u·u ¢ , (u 3 ) ¢ = 3u 2 u ¢ , … , (u n ) ¢ =n·u n–1 u ¢ .
Derivati i herësit.
Nese atehere  .
.
Tabela e derivateve
1. (Me)¢ =0
Për një funksion kompleks: nëse u=u(x), Se:
2. (X)¢ =1
3. (X α )¢ = α · Xα-1, A- çdo numër real.
 .
.
3. 
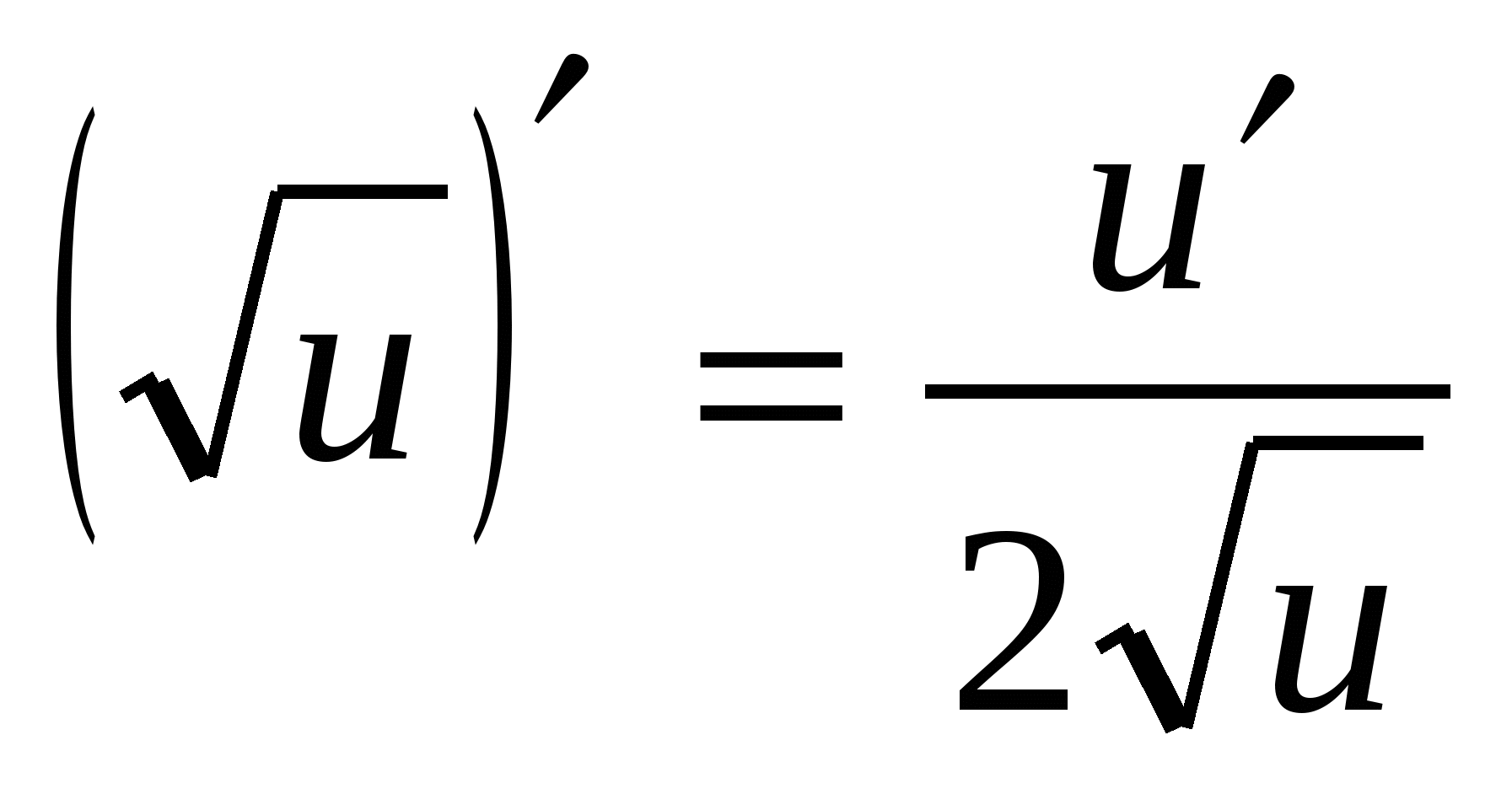
4. (A X ) ¢ =a X · ln A
4. 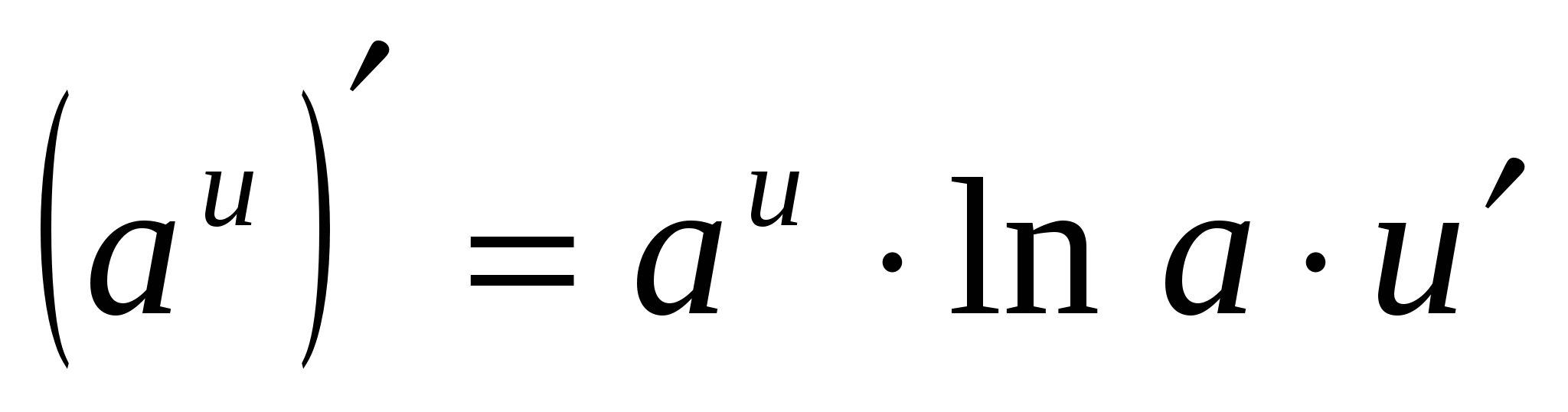
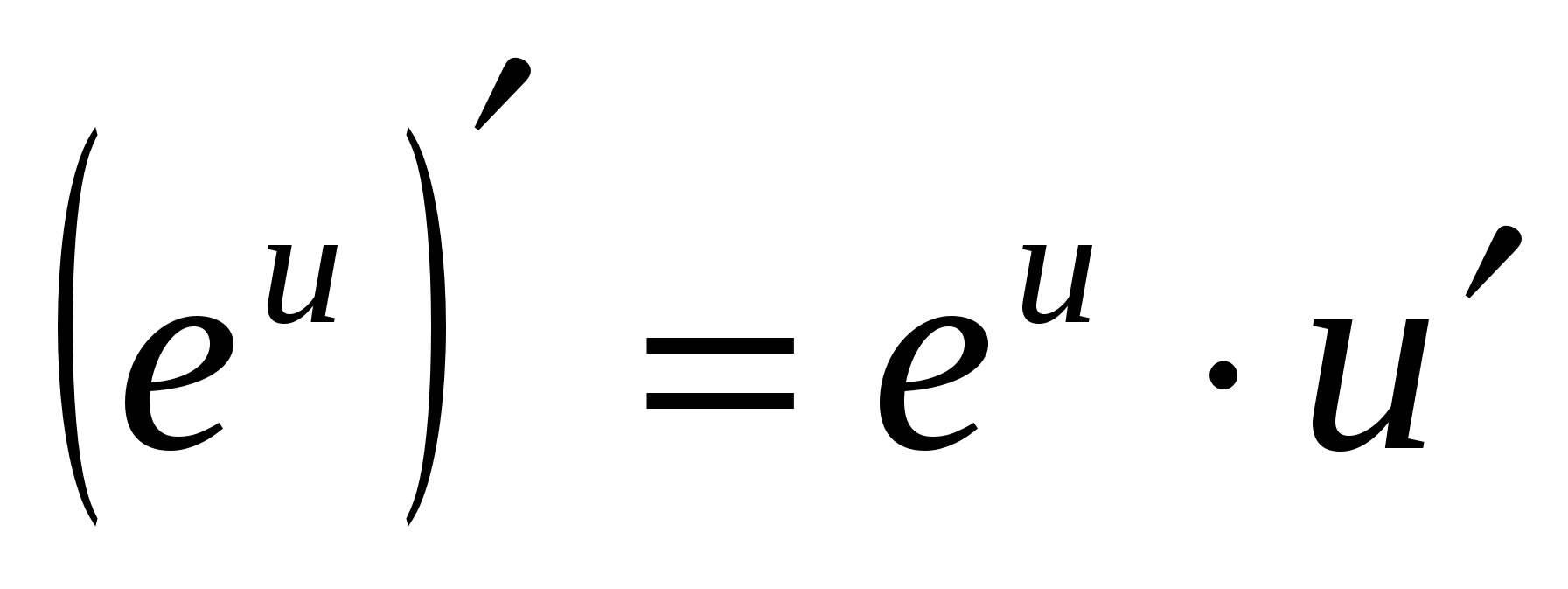
5. (log
a
x)
¢
=
 .
.
5. 

6. (mëkat x)¢ =cos x
6. 
7. (cos x)¢ = –sin x
7. 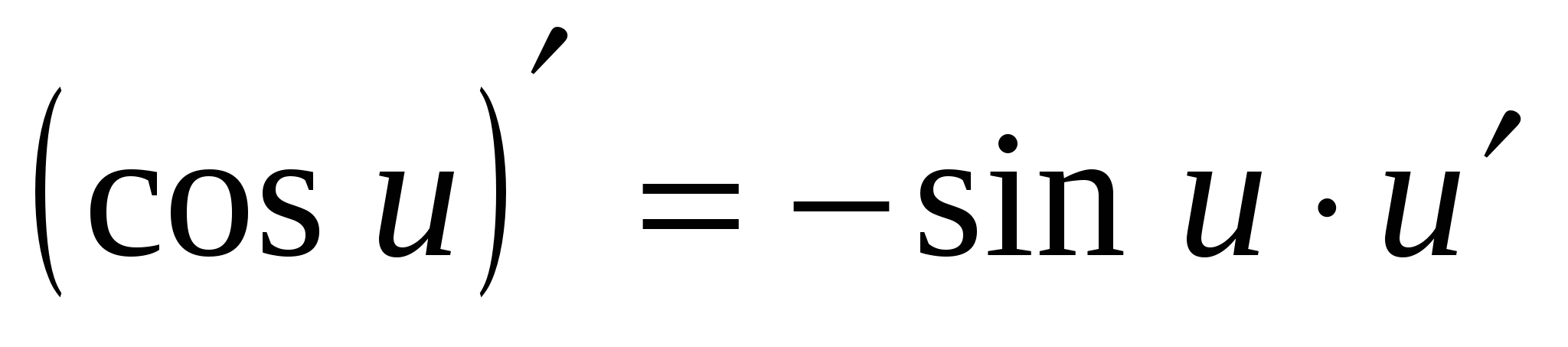
8. (tg x)¢
=
8. 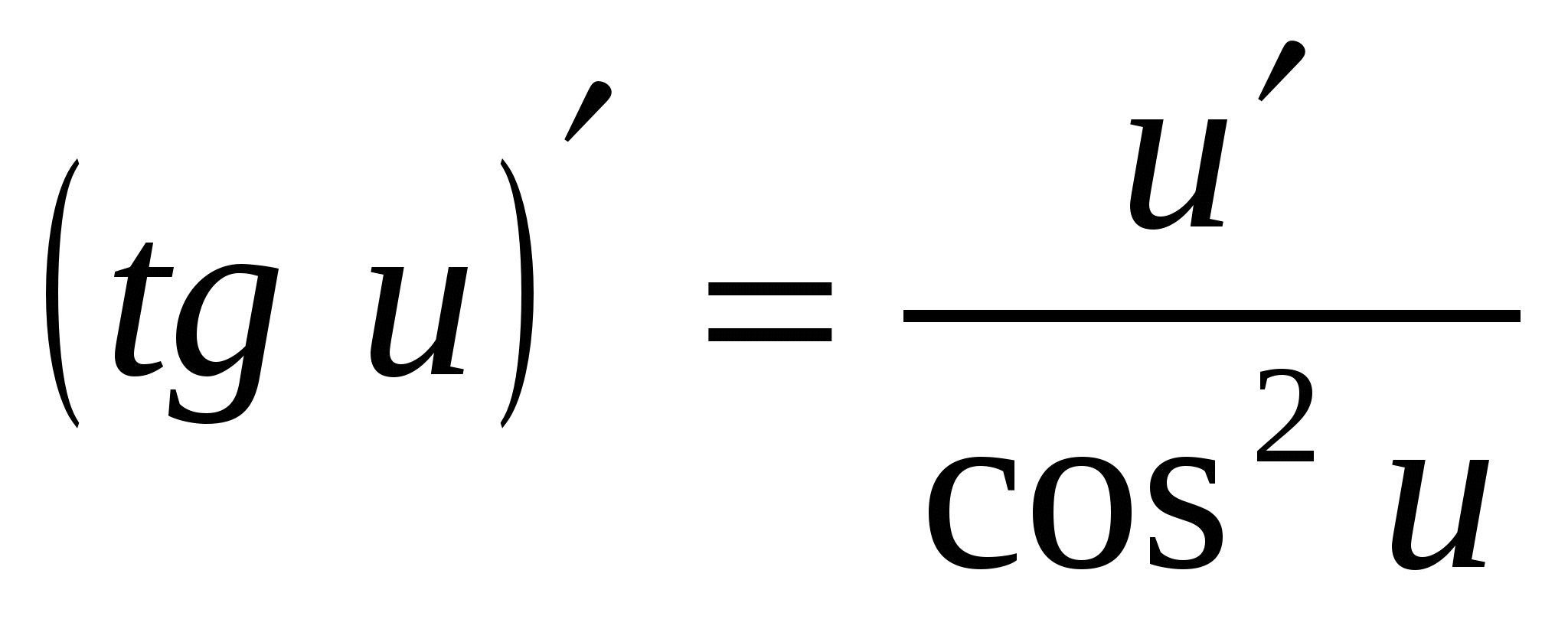
9. (ctg x)¢
=
9. 
10. 
10. 
11. 
11. 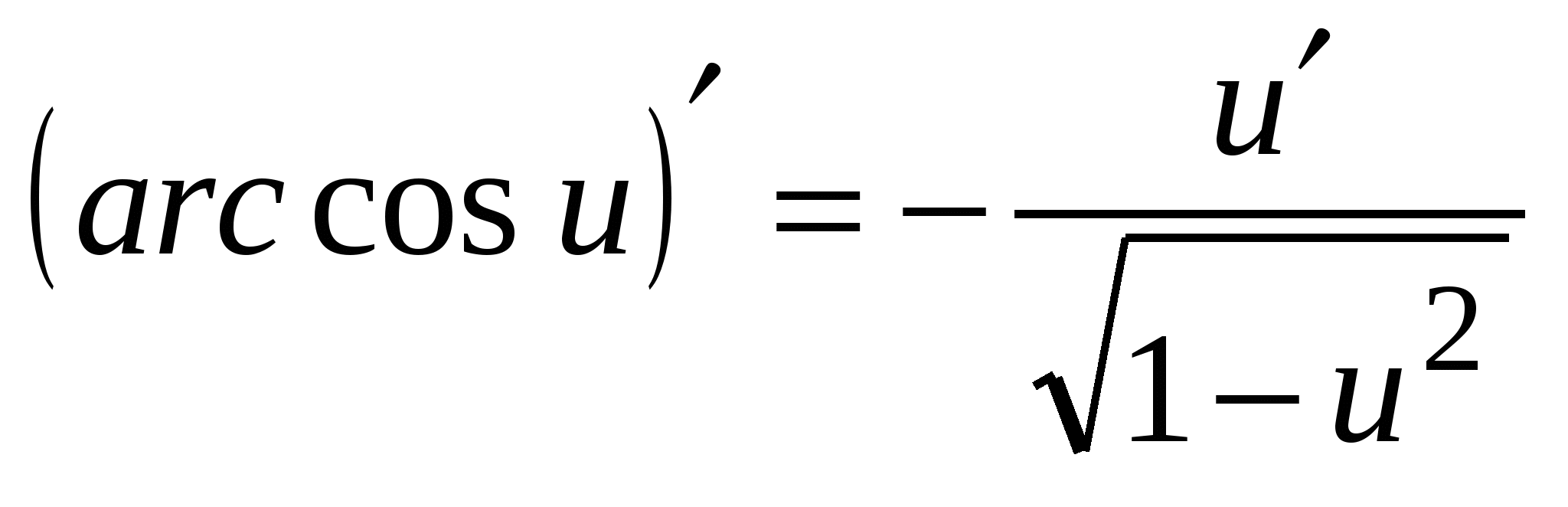
12. 
12. 
13. 
13. 
Shqyrtoni shembuj
Shembulli 1.
y=(3–2 sin 5x ) 4 | Ne aplikojmë formula derivative për Dhe α , mëkat u |
y ¢ =4·(3–2·sin5x) 3·(3–2sin5x) ¢ =4·(3–2· mëkat5x) 3 ·(0–2·cos5x·5) = –40·(3–2·sin5x) 3 .
Shembulli 2.
. 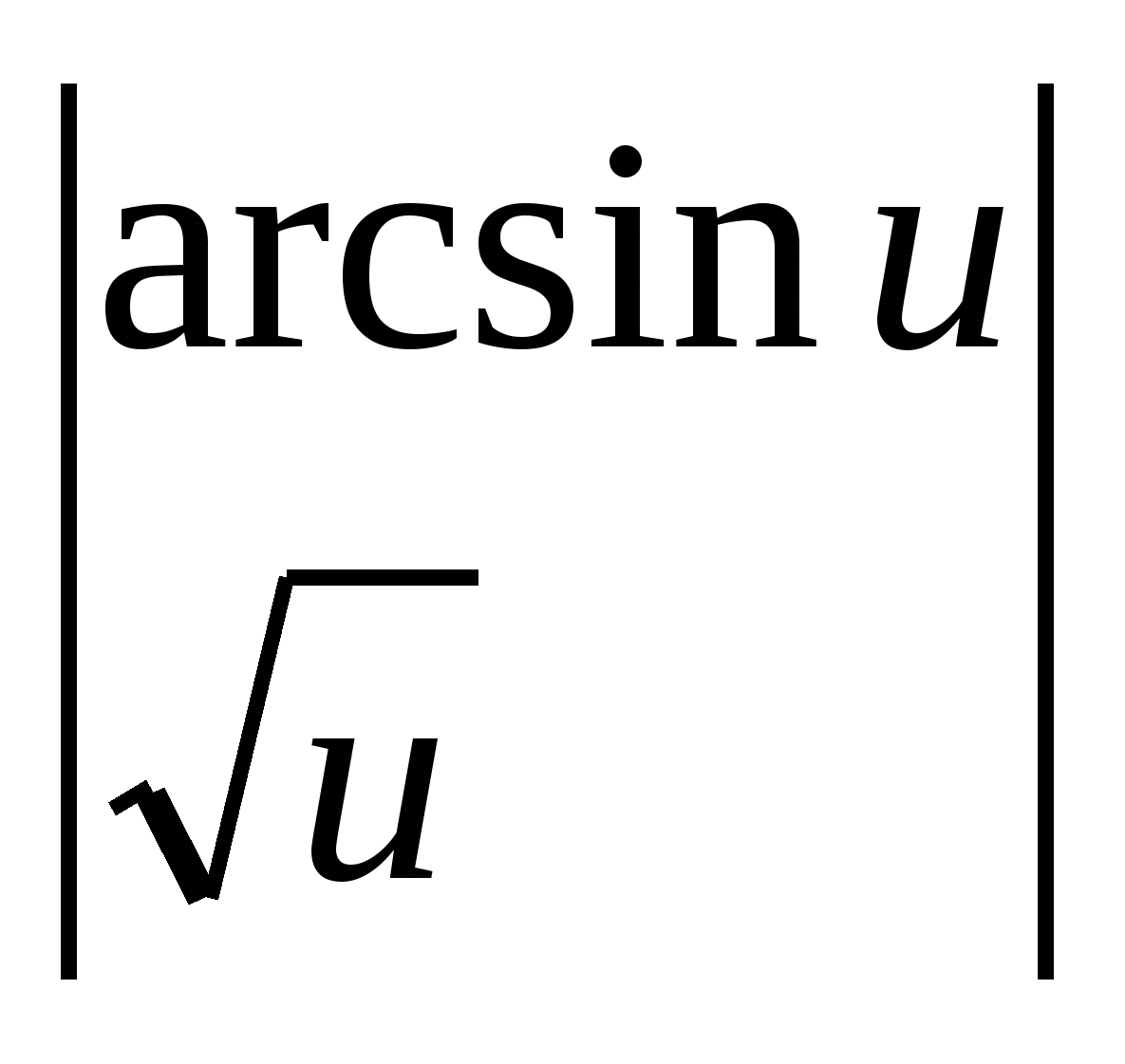

Shembulli 3.
 .
. 

Shembulli 4.



Shembulli 5.
 .
. 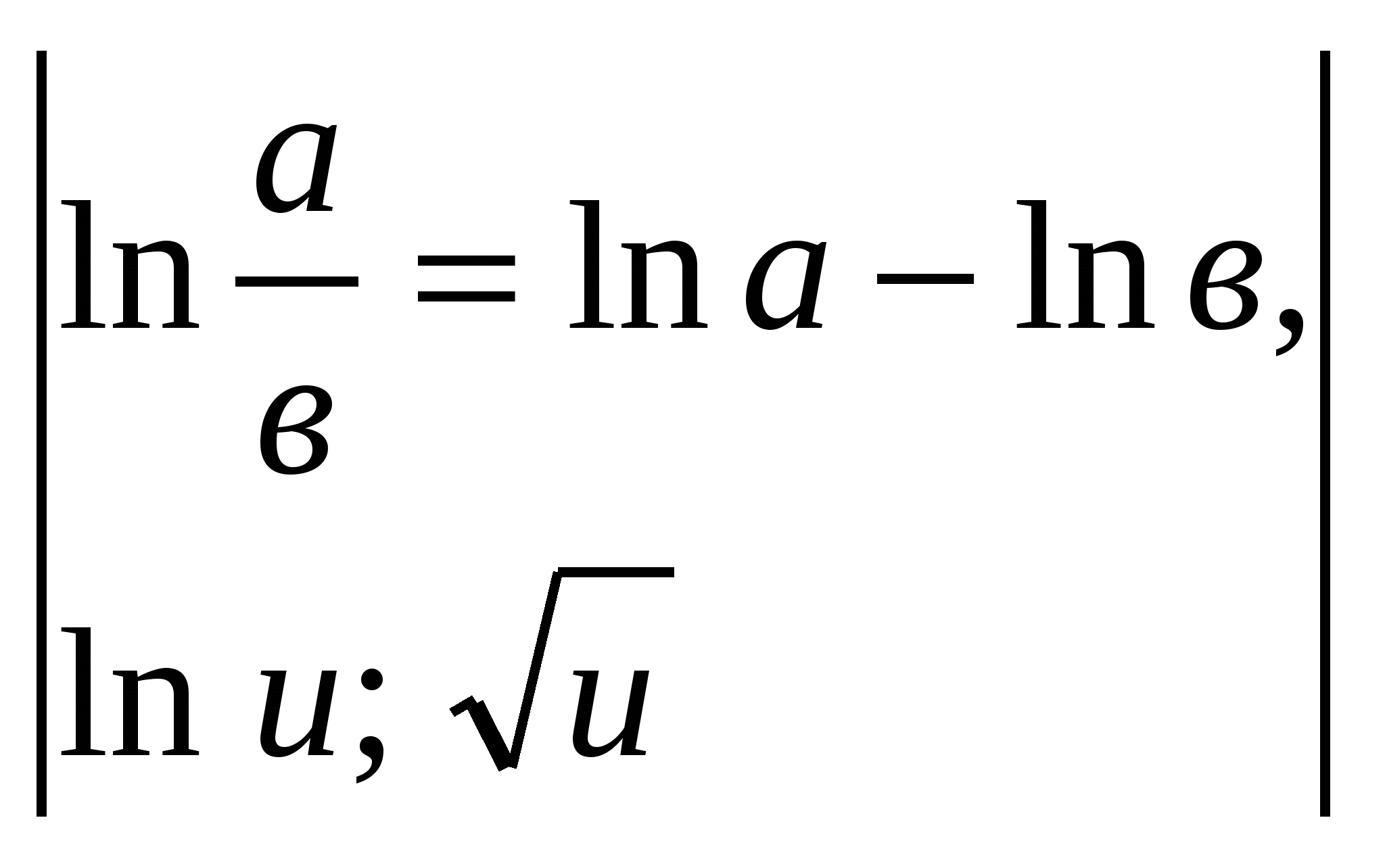

Ekstremi i funksionit
Studimi i një funksioni në një ekstrem është një nga aplikimet më të rëndësishme të derivateve. Le të shohim përkufizimin e minimumit dhe maksimumit, dhe si t'i gjejmë ato.
Lëreni funksionin ƒ( X) është i përcaktuar dhe i diferencueshëm në një grup dhe një pikë të caktuar X 0 është një pikë brenda saj.
Përkufizimi. Funksioni ƒ (X) në pikë X 0 ka maksimale(minimumi), nëse ka një fqinjësi të tillë të pikës X 0, që është për të gjithë X nga kjo zonë ƒ (X) < ƒ (X 0 ) (ƒ (X) > ƒ (X 0 )).
Pika X 0 quhet atëherë një pikë maksimale(minimumi).

Oriz. 1.
Tregohet një grafik i një funksioni që ka dy pikë maksimale ( X 1 dhe X 3) dhe dy pikë minimale ( X 2 dhe X 4), dhe vlera maksimale mund të jetë më e vogël se minimumi ( ƒ (X 1 ) < ƒ (X 4)). Kjo thekson faktin se ne e karakterizojmë singularitetin e një funksioni vetëm afër një pike të caktuar.
Vlerat e funksionit në pikat maksimale dhe minimale quhen vlera ekstreme ose ekstremet. Grafiku i mësipërm tregon se pikat ekstreme ( X 1 , X 2 , X 3 , X 4) përcaktoni intervalet e monotonitetit të funksionit, në secilën prej të cilave derivati ruan një shenjë të caktuar. Në pikat ekstreme, natyrisht, derivati shkon në zero. Le të formulojmë një teoremë rreth kusht i nevojshëm ekzistenca e një ekstremi.
Teorema. Nëse funksioni ƒ (X) në pikë X 0 ka një ekstrem, atëherë derivati i funksionit në këtë pikë është i barabartë me zero, d.m.th. ƒ¢ ( X 0)=0.
Le të vërejmë menjëherë se ky kusht nuk është i mjaftueshëm, d.m.th., deklarata e kundërt nuk është gjithmonë e vërtetë. Nga barazia ƒ ¢ ( X 0)= 0 nuk do të thotë domosdoshmërisht se në pikë X 0 ka një ekstrem.
Kjo konfirmohet nga një shembull me funksionin ƒ (X)=x 3 .
Ne do të gjejmë ƒ ¢ ( X)= 3X 2 . Në pikën X=0 ƒ ¢ (0)=0 . Por aq afër pikës sa të duash X=0 do të gjejmë X> 0, ku ƒ (X)=x 3 > 0, do të gjejmë X< 0, где ¦ (X)=X 3 < 0. Т. е. не существует какая-либо малая окрестность точки X=0, ku për të gjithë X vlera e funksionit në një pikë X=0 do të jetë më e madhja ose më e vogla. Prandaj pikë X=0 nuk është një pikë ekstreme.
Dikush mund të argumentojë ndryshe. Që nga derivati ƒ ¢ (x)=3x 2 , pastaj funksioni ƒ(x)=x 3 rritet për çdo x real dhe nuk ka ekstreme.
Pikat në të cilat plotësohet kushti i nevojshëm ekstrem (ƒ ¢ (x)=0) quhen kritike .
Natyrisht, tangjentja me grafikun e funksionit në pikat ku ƒ ¢ (x)=0, paralel me boshtin x Ox .
Gjendje e mjaftueshme ekstremi është dhënë në teoremat e mëposhtme.
Teorema 1. Nëse X 0 është pika kritike e funksionit dhe kur kalon nëpër të derivati ndryshon shenjën, atëherë X 0 është një pikë ekstreme, domethënë, nëse derivati ndryshon shenjën nga plus në minus, është një pikë maksimale, dhe nëse ndryshon shenjën nga minus në plus, është një pikë minimale.
Vini re se nuk ka ekstrem në një pikë nëse derivati nuk ndryshon shenjë. Rregulli për studimin e ekstremit duke përdorur derivatin e parë njihet nga kursi shkollor. Ndonjëherë është më e përshtatshme të formulohet një kusht i mjaftueshëm për një ekstrem duke përdorur derivatin e dytë.
Lëreni funksionin ƒ( X) është dy herë i diferencueshëm në disa fusha (d.m.th. ƒ( X) ka ƒ¢ ( X) Dhe ƒ ¢¢ ( X)).
Teorema 2. Nëse X 0 – pika kritike e funksionit ƒ(x) dhe ƒ ¢¢ (X 0 ) > 0 , Kjo X 0 – pikë minimale, nëse ƒ ¢¢ (X 0 ) < 0, то X 0 - pikë maksimale.
Duke përdorur derivatin e dytë, përcaktohet konveksiteti ose konkaviteti i grafikut të një funksioni.
Konveksitet, konkavitet. Pika e lakimit.
Lakorja y=ƒ(X) quhet në mënyrë konvekseth më poshtë ndonjë prej saj tangjente
ƒ ¢¢ ( X) < 0.
Lakorja y=ƒ(X) quhet konkave në një interval nëse shtrihen të gjitha pikat e kurbës më të larta ndonjë prej saj tangjente në këtë interval. Pastaj në këtë interval
ƒ ¢¢(x) > 0
Përkufizimi. Pika e lakimit Një kurbë është një pikë ku nga njëra anë kurba është konveks dhe nga ana tjetër është konkave.
Në pikën e përkuljes ƒ ¢¢ ( X)=0.
Pra, shenja e derivatit të dytë (si dhe shenja e vetë funksionit dhe derivatit të parë të tij) tregon veçoritë e grafikut të funksionit. Le t'i shikojmë ato përsëri.
Nëse për të gjithë X në intervalin ( A, b) ƒ (X) > 0 (ƒ (X) < 0), atëherë grafiku qëndron sipër (poshtë) boshtit x.
Nëse për të gjithë X në intervalin ( A, b) ƒ ¢ ( X) > 0 (ƒ ¢ ( X) < 0), то функция на (A, b) rritet (zvogëlohet).
Nëse për të gjithë X në intervalin ( A, b) ƒ ¢¢ ( X) > 0 (ƒ ¢¢ ( X) < 0), то график на (A, b) konkave (konveks).
Ekuacioni ƒ( X)=0 përcakton “zerot” e funksionit, pra pikat e prerjes së grafikut me boshtin Ox.
Ekuacioni ƒ ¢ ( X)=0 përcakton pikat kritike.
Ekuacioni ƒ ¢¢ ( X)=0 përcakton pikat e mundshme të lakimit.
Skema e studimit të funksionit
Për të studiuar funksionin ƒ (X) dhe komplot y=ƒ(X) duhet të gjendet:
1) fusha e përcaktimit të funksionit dhe pika e kryqëzimit të grafikut me boshtet koordinative;
2) intervalet e monotonisë;
3) pikat e vlerave ekstreme dhe funksionale në këto pika;
4) intervalet e konveksitetit dhe konkavitetit të grafikut;
5) pikat e lakimit të grafikut;
6) ndërtoni në një sistem koordinativ kartezian të gjitha pikat e marra (nganjëherë, për të sqaruar grafikun, fitohen pika shtesë) dhe vetë grafikun.
Vlerat më të vogla dhe më të mëdha të një funksioni në një segment
Kur zgjidhni disa probleme të metodës së optimizimit, është e rëndësishme të jeni në gjendje të gjeni vlerat më të vogla ose më të mëdha të një funksioni në një segment të caktuar. Funksioni i arrin këto vlera ose në pikat kritike ose në skajet e segmentit.
Skema e kërkimit vlerat më të vogla dhe më të mëdha të funksionit ƒ (X) në segmentin [ A, b].
1. Gjeni derivatin e funksionit ƒ ¢ ( X).
2. Gjeni pikat kritike nga ekuacioni ƒ ¢ ( X)=0.
3. Zgjidhni ato pika kritike që i përkasin këtij segmenti [ A, b] dhe gjeni vlerën e funksionit ƒ (X) në çdo pikë të tillë.
4. Llogaritni vlerat e funksionit ƒ (X) në skajet e segmentit: ƒ( A) dhe ƒ( b).
5. Nga vlerat e fituara të funksionit zgjidhet më i madhi (më i madhi) dhe më i vogli (më i vogli).
Shembulli 2.
Gjeni vlerat më të mëdha dhe më të vogla të një funksioni ƒ(x)=X 3 – 9x 2 +24х–10 në segment.
1. ƒ ¢ ( X)= 3X 2 – 9·2 X 2 + 24.
2. ƒ ¢ ( X)=0, 3(X 2 –6X+8)=0, X 1 =2, X 2 =4.
3. Pika x 2 =4 nuk i përket segmentit. Prandaj, ne llogarisim vlerën e funksionit vetëm në pikë X 1 =2
ƒ(2)=2 3 –9·2 2 +24·2–10=10.
4. Vlerat e funksionit në skajet e segmentit: ƒ(0)= –10, ƒ(3)=3 3 –9·3 2 +24·3–10, ƒ(3)=8.
5. Vlerat e marra:
ƒ(2)=10, ƒ(0)= –10, ƒ(3)=8.
Vlera më e lartë është 10 dhe arrihet në pikë X=2. Më i vogli është i barabartë me –10 dhe arrihet në pikë X=0.
Shembulli 3.
Gjeni intervalet e konveksitetit dhe konkavitetit dhe pikat e lakimit të kurbës y=x+36X 2 –2X 3 –X 4 .
Fusha e përcaktimit të këtij funksioni është bashkësia e të gjithë numrave realë, d.m.th. XЄ(–∞, +∞).
Le të gjejmë derivatin e dytë.
në¢ =1+72 X–6X 2 –4X 3 .
n뢢 =72–12 X–12X 2 = –12(X 2 +X–6).
Nga barazimi. n뢢 =0 marrim abshisën e pikës së lakimit:
–12(X 2 +X–6)=0 X 1 = –3; X 2 =2.
Le të përcaktojmë shenjën n뢢 në intervale
(–∞; –3), (–3; 2), (2, +∞).
X
(–∞, –3)
(–3; 2)
(2; +∞)
n뢢
forma e kurbës
konveks
lakimi
konkave
lakimi
konveks
Le të gjejmë ordinatat e pikave të lakimit:
në(–3)=726; M 1 (–3; 726) – pika e lakimit
në(2)=114; M 2 (2; 114) - pika e lakimit.
Në intervalin (–3; 2) kurba është konkave. Në intervalet (–∞; –3) dhe (2; +∞) – konveks.
Shembuj të detyrave
Detyra nr. 1.
Gjeni pikat e ndërprerjes së funksionit dhe vizatoni grafikun

Funksioni ƒ (X) është përcaktuar për të gjitha realet X dhe është i vazhdueshëm në secilin nga intervalet e treguara: (–∞; –1), [–1; 0], (0, +∞). Le të shqyrtojmë funksionin ƒ (X) për vazhdimësi në pika X= –1 dhe X=0.
Për ta bërë këtë, ne do të gjejmë kufij të njëanshëm në secilën nga këto pika.

Meqenëse kufijtë e njëanshëm janë të ndryshëm, atëherë X = –1 – pika e ndërprerjes së llojit të parë.
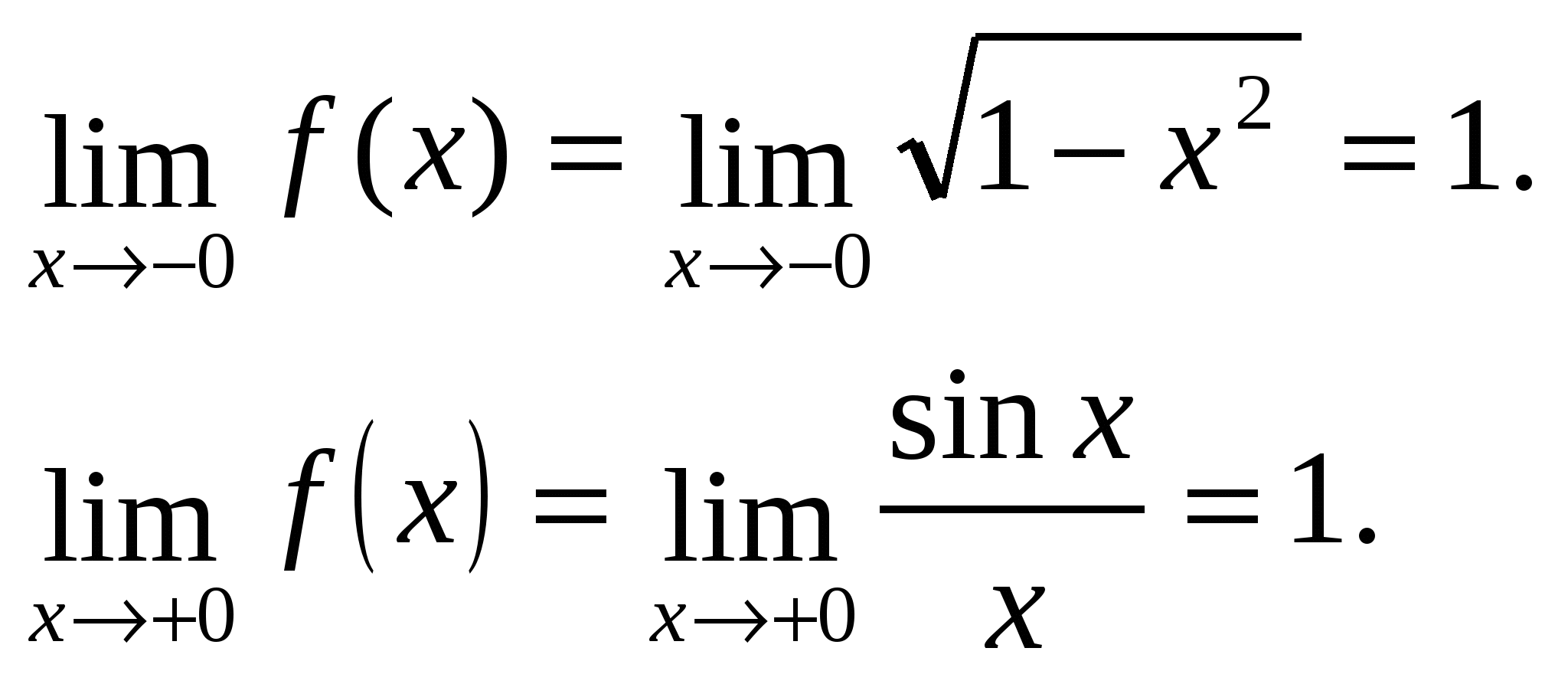
Kufijtë e njëanshëm janë të barabartë, pra në pikën x=0 ka një kufi të funksionit dhe 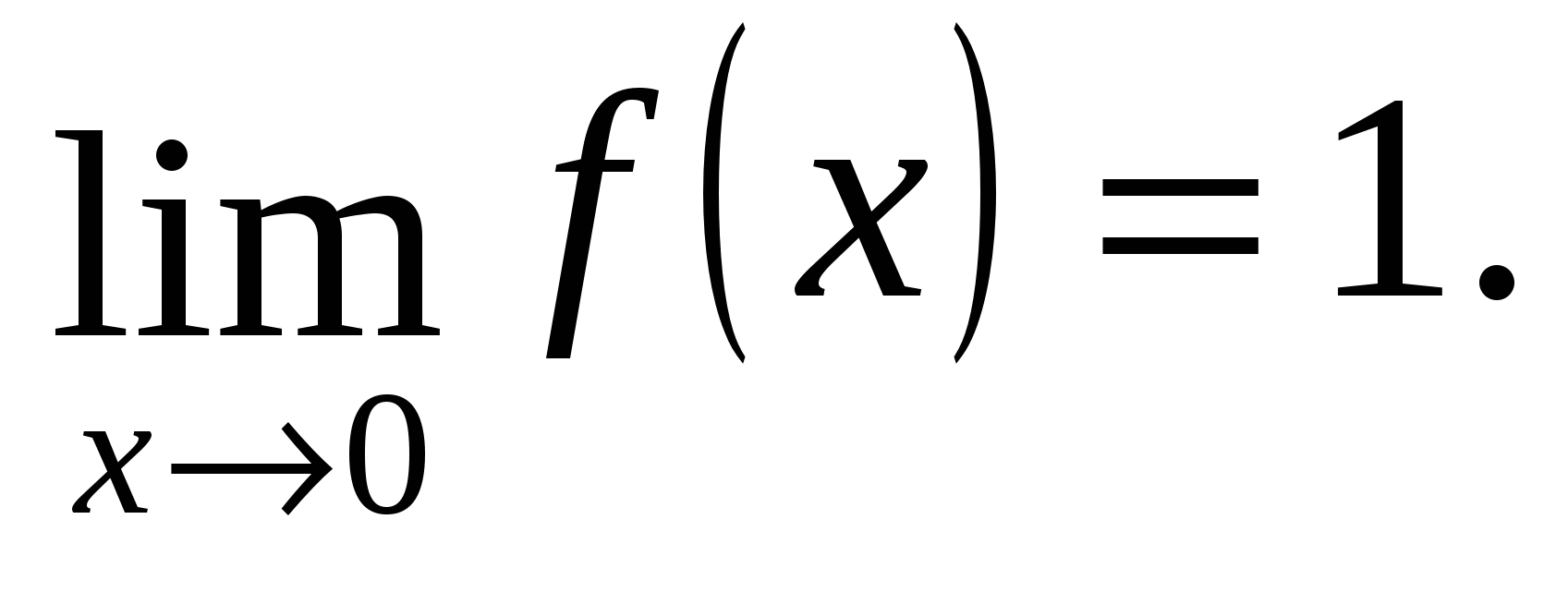
Le ta krahasojmë këtë kufi me vlerën e funksionit në pikën: 
Sepse  pastaj në në x=0 funksioni ƒ(x) është i vazhdueshëm.
pastaj në në x=0 funksioni ƒ(x) është i vazhdueshëm.
Le të paraqesim funksionin ƒ (X), duke pasur parasysh se
1)  - ekuacioni i një vije të drejtë,
- ekuacioni i një vije të drejtë,
2)  – ekuacioni i gjysmërrethit të sipërm
– ekuacioni i gjysmërrethit të sipërm  me qendër në origjinë dhe rreze të barabartë me unitetin, dhe nën kushtin –1 £ X ekuacioni 0 £
me qendër në origjinë dhe rreze të barabartë me unitetin, dhe nën kushtin –1 £ X ekuacioni 0 £  përcakton një çerek rrethi.
përcakton një çerek rrethi.
3) për X > 0 grafiku jepet nga ekuacioni  . Pikat e kryqëzimit të kësaj lakore me boshtin Ox i gjejmë nga ekuacioni
. Pikat e kryqëzimit të kësaj lakore me boshtin Ox i gjejmë nga ekuacioni 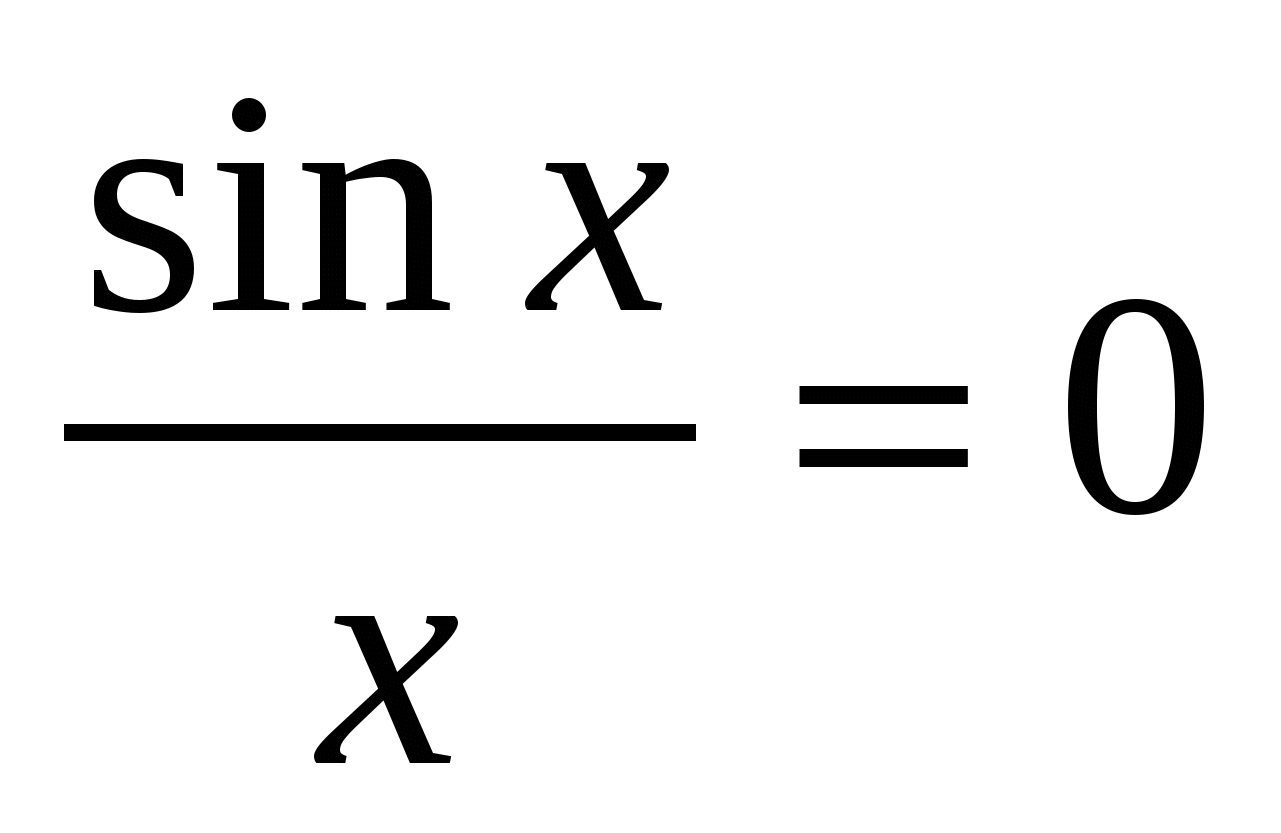 për x > 0. x= π
n, Ku n
=1, 2, 3, 4,
për x > 0. x= π
n, Ku n
=1, 2, 3, 4,

Oriz. 2.
Detyra nr. 2.
Shkruani ekuacionet për tangjentet në një vijë  në pikat ku X=0 dhe X=4. Gjeni pikën e prerjes së tangjentave dhe këndin ndërmjet tyre. Bëni një vizatim.
në pikat ku X=0 dhe X=4. Gjeni pikën e prerjes së tangjentave dhe këndin ndërmjet tyre. Bëni një vizatim.
Ekuacioni i një tangjente në një drejtëz y=ƒ(x) duket si
Ku në 0 =ƒ( X 0).
Në pikën X=0 në(0)=ƒ(0)=5.
në¢ =ƒ ¢ (X)=X–3 ƒ¢ (0)= –3.
M 1 (0, 5) ka formën y- 5= –3(X–0) ose
y= –3X+5.
Në pikën X=4 në(4)=ƒ(4)=1. ƒ¢ (4)=4–3=1.
Ekuacioni i një tangjente në një pikë M 2 (4, 1) ka formën y- 1=X-4 ose
y=x–3.
Pikën e kryqëzimit të tangjentave e marrim duke zgjidhur sistemin

Pika e kryqëzimit M 3 (2, –1).
Këndi φ ndërmjet tangjentëve gjejmë nga formula:
 ,
,
Ku k 1 = –3; k 2 =1 – koeficientët këndorë të tangjentëve.
 .
.
Këndi φ =arctg 2.
Le të ndërtojmë këtë linjë  – një parabolë me kulm në pikën ku X=3, sepse në¢
=0 në X=3. Ne do të gjejmë
– një parabolë me kulm në pikën ku X=3, sepse në¢
=0 në X=3. Ne do të gjejmë  . Pika M 4 (3;
. Pika M 4 (3;  ) është kulmi i parabolës.
) është kulmi i parabolës.
R 
është. 3.
Detyra nr. 3.
Funksioni i eksplorimit 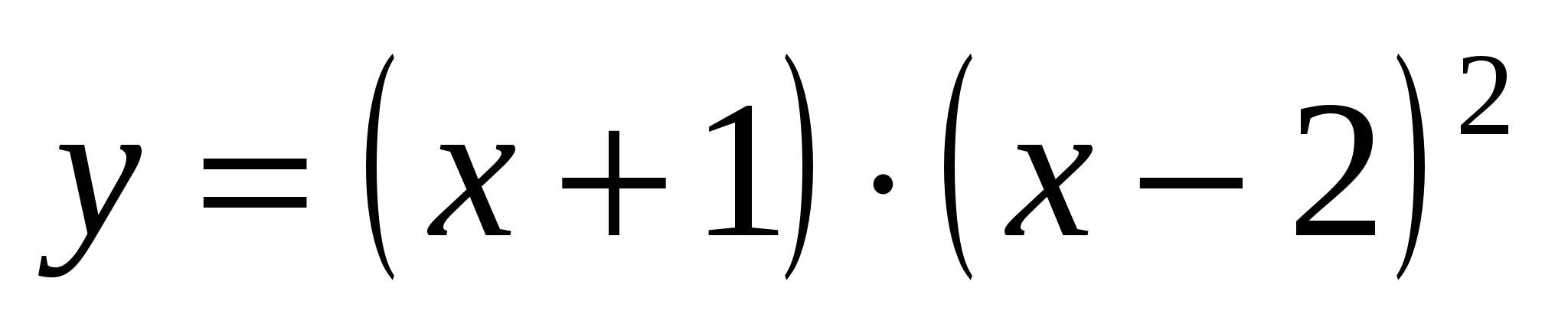 dhe komplotoni atë.
dhe komplotoni atë.
1. Ky funksion është një polinom (mund të hapni kllapat, marrim një polinom të shkallës së tretë), prandaj është i përcaktuar, i vazhdueshëm dhe i diferencueshëm për çdo X.
2. Të gjejmë derivatin.
 .
.
Nga barazimi. në¢ =0 le të gjejmë pikat kritike: 3 X·( X–2)=0, X 1 =0, X 2 =2.
Le t'i eksplorojmë ato.
X
(–∞, 0)
(0; 2)
(2; +∞)
në ¢
në
3. Pra, funksioni rritet në intervalet (–∞, 0) dhe (2, +∞), zvogëlohet në intervalin (0; 2), ka një maksimum në x=0 dhe një minimum në x=2:
në max = në(0)=4; në min = në(2)=0.
4. Le të gjejmë derivatin e dytë.
n뢢 = 6·( X-1).
Lakorja është konvekse ku n뢢 < 0, т. е. 6·(X–1) < 0, X < 1.
Kurba është konkave ku n뢢 > 0, d.m.th. X > 1.
Pra, në intervalin (–∞, 1) kurba është konvekse; dhe në intervalin (1, +∞) është konkave.
5. Pikën e lakimit e gjejmë nga ekuacioni n뢢 =0. Kështu, X=1 – abshisa e pikës së lakimit, sepse kjo pikë ndan intervalet e konveksitetit dhe konkavitetit të kurbës. Ordinata e pikës së lakimit: në(1)=2.
Grafiku i një funksioni në=(X+1)·( X–2) 2 pret boshtin Ox në në=0, pra kur X= –1 dhe X=2;
kalon aksin Oy në X=0, pra kur në=4. Ne morëm tre pikë: (–1; 0), (2; 0), (0; 4). Të gjitha pikat e marra do t'i fusim në tabelë, duke shtuar ato ngjitur me to.
–2
–1



–16


është. 4 Lakorja y=(x+1)(x–2) 2.
Detyra nr. 1
Ne ju prezantojmë me detyra që mund të kenë një, dy, tre ose më shumë përgjigje të sakta. Rrethoni numrat e të gjitha përgjigjeve të sakta.
1. Nëse  pastaj funksioni
pastaj funksioni
1) në rritje
2) në rënie
3) konstante
2. Nëse
1) Në rritje
2) Në rënie
3. Nëse  , pastaj funksioni
, pastaj funksioni
1) Në rritje
2) Në rënie
4. Nëse  , pastaj funksioni
, pastaj funksioni
1) Në rritje 3) Në rënie
2) Konstante 4) Monotone
5. Funksioni  Është
Është
1) Madje
2) Madje as
3) as çift e as tek
4) Periodik
5) Jo periodik
6) Trigonometrike
7) Fillore
6. Funksioni  Është
Është
1) madje
2) tek
3) as çift e as tek
4) periodike
5) jo periodike
6) trigonometrike
7) elementare
2) Weierstrass 4) Dirichlet 6) Leibniz
8) Zgjidhja  Ekuacionet
Ekuacionet
1) 0 3) 0 dhe 3 5) 2 7) 3
2) 2 dhe 3 4) 2 6) -5 dhe 1 8) 5 dhe 1
9) zgjidhja e pabarazisë 
1) ( ; 1) 3) (
; 1) 3) ( ; 1) 5) (-
; 1) 5) (- ;1)
;1)
2) (1; 5) 4) (2;  ) 6)
) 6) 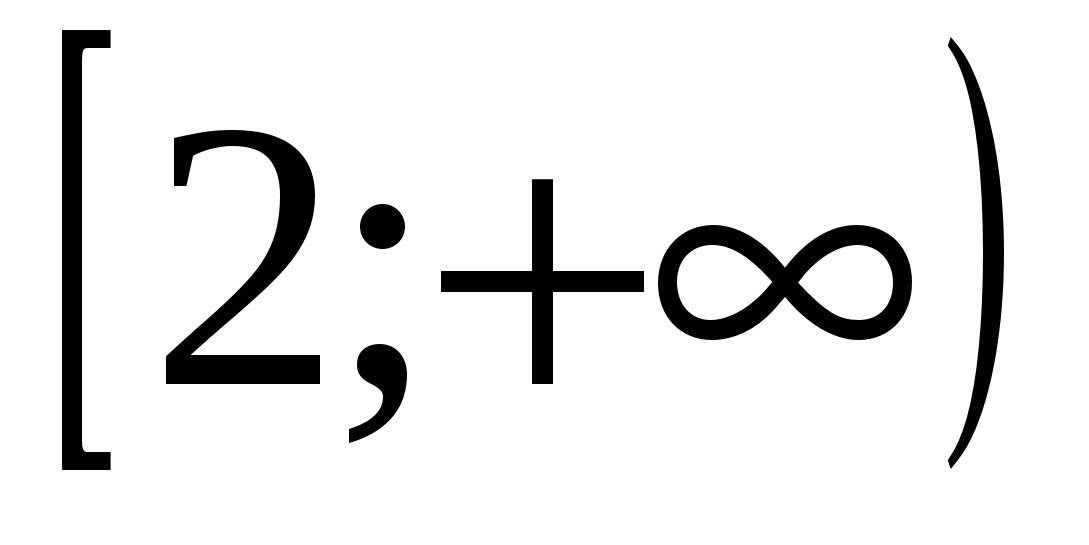
10) Metoda  Shuma është gjetur
Shuma është gjetur
1) vektorë
2) drejt
3) segment
11) Nëse  , pastaj funksioni
, pastaj funksioni
1) Konkave 3) Konveks 5) Në rënie
2) Monotonik 4) Rritës 6) Konstant
12) domeni i përcaktimit të funksionit është i barabartë me 
1) ( ;0)
;0)
2) (0;  )
)
3) (- ;
; )
)
4) (0;1)
5) 
6) 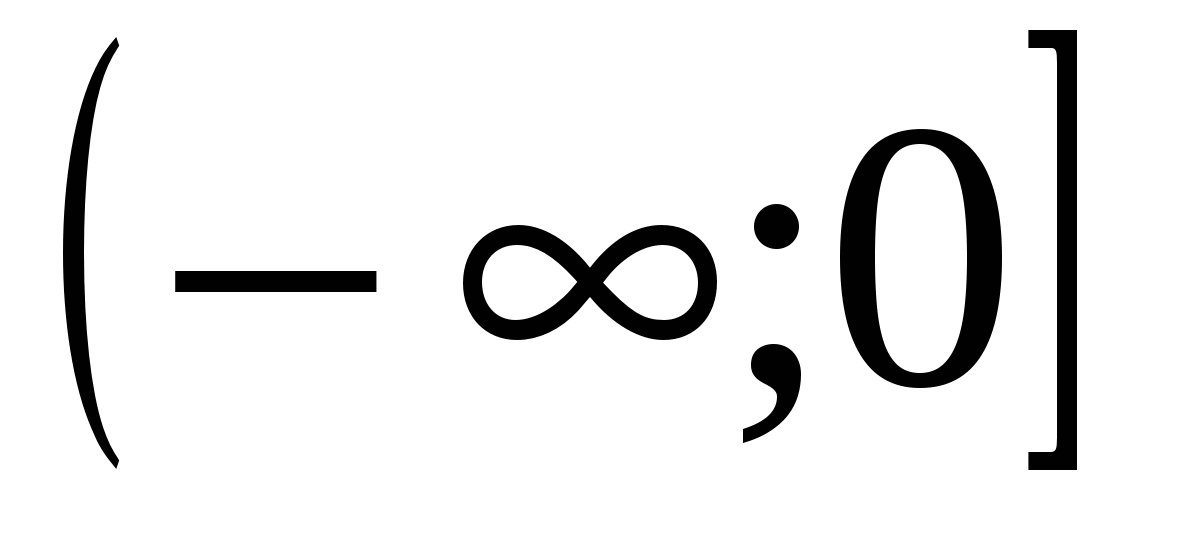
7) (-1;1)
8) 
9) 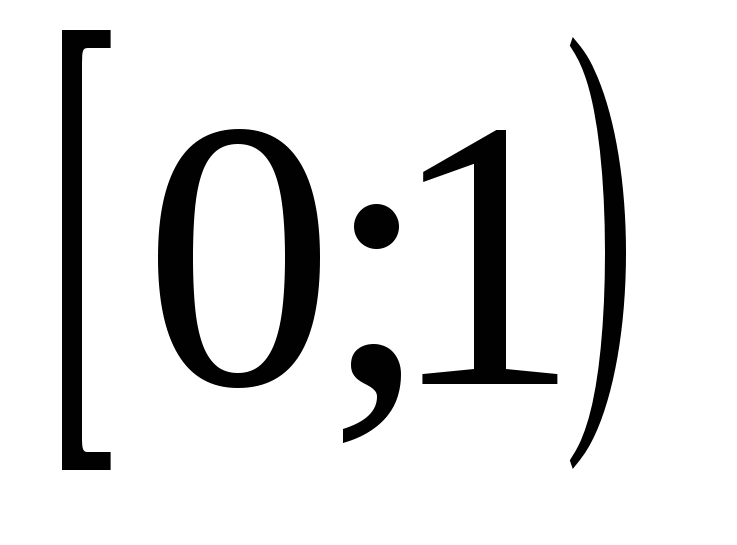
13) funksion  është
është
1) tregues
2) trigonometrike
3) fuqia
4) logaritmike
14) nëse funksionet y = x  atëherë ajo është
atëherë ajo është 
1) madje
2) tek
3) as çift e as tek
15) funksion  në
në  është
është

 .
.


