Testet për konvergjencën e integraleve jo të duhura. Si të llogarisni një integral të gabuar dhe të zbuloni konvergjencën e tij. Përkufizimi dhe vetitë themelore

Teorema 12.11 (test për krahasimin e integraleve jo të duhura). Le të jenë funksionet f(x) dhe g(x) të vazhdueshme në intervalin [a, ">) dhe të plotësojnë kushtin 0 fix) ?(x) në të. Pastaj nga konvergjenca e integralit

integrali konvergon

dhe anasjelltas, nga divergjenca e integralit (12.64) vjen divergjenca e integralit (12.63).

Dëshmi. Le të prezantojmë shënimin e mëposhtëm:

Funksioni P(K) nuk është në rënie; në fakt, nëse dhe unë 2, atëherë

J rregulloj) dx>0, dhe pastaj

Le të marrim një sekuencë vlerash (/?„) -> ">; pastaj sekuenca përkatëse e vlerave të funksionit (F(R n))është monoton dhe jo në rënie. Le të konvergojë integrali (12.63), pastaj sekuenca (67 ( R ajo)) është e kufizuar; por atëherë edhe sekuenca është e kufizuar (F(/?„)), që do të thotë se nga Teorema 7.13 ajo konvergon. Prandaj ka një kufi F(R) në R-+ «>, d.m.th. integrali (12.64) konvergon.

Tani le të vërtetojmë pjesën e dytë të teoremës; le të divergjojë integrali (12.64). Nëse supozojmë se integrali (12.63) konvergjon, atëherë, sipas asaj që u vërtetua më sipër, duhet të konvergojë edhe integrali (12.64), gjë që bie ndesh me kushtin. Teorema është vërtetuar. ?

Komentoni. Një kriter i ngjashëm krahasimi është gjithashtu i vlefshëm për integrale të pahijshme të llojit të dytë. Nëse funksionet /(x) dhe g (X) e vazhdueshme në gjysmë-interval [a>b) dhe për të gjitha pikat në ndonjë fqinjësi të pikës njëjës b përfunduar

kushtet 0 (x), atëherë nga konvergjenca e integralit Jg(x)dx del se

divergjenca e integralit J/(x)dx, dhe nga divergjenca e integralit J/(x)dx -

fuqia e integralit Jg(x)dx.

Le të shqyrtojmë shembuj për të studiuar konvergjencën e integraleve jo të duhura.

Shembulli 27. T. ^-.

X 3 (1 + e L)

Zgjidhje. Le të krahasojmë integrandin në këtë integral me funksionin

Dg. Është e qartë se -r-

X g* (1+0 x J

gral J-jdx konvergon; prandaj, në bazë të kriterit të krahasimit, 1 i dhënë X

integral nal.

Shembulli 28. I-.

Zgjidhje. Krahasimi i integrandit të këtij integrali me funksionin 1/x,

shohim se (1 + Në x)/x > 1/x në intervalin 1

diversifikohet, prandaj, për krahasim, edhe ky integral divergjent.

Si përfundim, ne paraqesim pa prova kriterin Cauchy për konvergjencën e një integrali të papërshtatshëm të llojit të parë.

12.10.4. Konvergjenca absolute dhe e kushtëzuar e integraleve jo të duhura

Përkufizimi 5. Një integral jo i duhur J/(x)dx quhet absolutisht

konvergjente, nëse integrali J|/(x)|dx konvergjon.

Përkufizimi 6. Integrali jo i duhur J /(x) dx quhet kushtimisht të ngjashme

të qëndrueshme, nëse konvergon dhe integrali J|/(x)|dx divergon.

Vini re se konvergjenca absolute e integralit nënkupton konvergjencën e tij për shkak të vlerësimit 3 integral i caktuar dhe kriteri Cauchy.

Teorema 12.13 (testi Dirichlet-Abel*). Le të jetë funksioni /(x) i vazhdueshëm dhe të ketë një antiderivativ të kufizuar F(x) në intervalin [a, «>], dhe funksioni g(x) ka një derivat të vazhdueshëm në këtë interval, nuk rritet dhe tenton në zero si x -> ©o. Pastaj integrali jo i duhur

konvergon.

Dëshmi. Le të zbatojmë integrimin sipas pjesëve në integralin J /(x)g(x)dx

në një segment arbitrar R R" Me [ A, °°). Ne kemi:

Teorema 12.12. Që integrali i papërshtatshëm (12.64) të konvergojë, është e nevojshme dhe e mjaftueshme që për çdo e > 0 mund të gjendet një numër i tillë. A> 0, e cila për çdo R" dhe /?", më e madhe se A, pabarazia vlen:

Sipas kushteve të teoremës F(x) kufizuar, d.m.th. |F(x)| K. Funksioni g(x) nuk rritet dhe tenton në zero si x -” “>, që do të thotë. g(x)> 0, a g"(x)

Abel Niels Henrik (1802-1829) - matematikan norvegjez.

Meqenëse, sipas kushteve të teoremës, g(x) -» 0 për x -> ©°, për një numër arbitrar e > 0 mund të gjejmë numrin A> e tillë që kur R" > L pabarazia do të plotësohet g(R") Duke e zëvendësuar këtë me vlerësimin (12.68), marrim:

që i përgjigjet kriterit Cauchy për konvergjencën e integralit (12.66). Teorema është vërtetuar. ?

Le të shqyrtojmë shembuj të përdorimit të testit Dirichlet-Abel për konvergjencën e integraleve jo të duhura.

Shembulli 29. f^^dx, a>0.

Zgjidhje. Le të vendosim /(x) = mëkat x, g(x)= l/x"; është e lehtë të verifikohet se plotësohen të gjitha kushtet e teoremës, domethënë ky integral konvergjon. Për një > 1, ky integral

ral konvergon absolutisht. Në të vërtetë, |mëkat x/xP 1/d L, integral J(l/x e)dx

konvergon, d.m.th. Me kriterin e krahasimit (teorema 12.11), ky integral gjithashtu konvergon absolutisht.

Shembulli 30. Jsin x 2 dx - integral Fresnel, o

Zgjidhje. Le ta paraqesim këtë integral si një shumë:

Që nga mëkati x 2 - funksion të vazhdueshëm në intervalin (0, 1J, integrali i parë në (12.69) ekziston. Për të përcaktuar konvergjencën e integralit të pahijshëm në anën e djathtë të (12.69), vendosim /(x) = x sin x 2, g(x) = 1/x. Pastaj për funksionin /(x) antiderivati F(x) = -cosx 2 /!është i kufizuar në intervalin |1, ">), dhe #(x) është pozitiv, tenton në zero si x -" °° dhe ka një derivat të vazhdueshëm në (1, ©о). Kjo do të thotë se sipas kriterit Dirichlet-Abel, integrali i dytë në (12.69) konvergon, d.m.th. integrali Fresnel gjithashtu konvergon.

Siç e dini, gjetja e integralit mund të jetë një detyrë mjaft e vështirë. Do të ishte një zhgënjim i madh të filloni të llogaritni një integral të gabuar dhe të zbuloni në fund të rrugës që ai ndryshon. Prandaj, me interes janë metodat që lejojnë, pa llogaritje serioze të bazuara në një lloj funksioni, të nxjerrim një përfundim në lidhje me konvergjencën ose divergjencën e një integrali jo të duhur. Teorema e parë dhe e dytë e krahasimit, të cilat do të diskutohen më poshtë, ndihmojnë shumë në studimin e integraleve jo të duhura për konvergjencë.

Le të jetë f(x)?0. Pastaj funksionet

janë në rritje monotonike në variablat t ose -g (pasi marrim g>0, -g priret në zero nga e majta). Nëse, ndërsa argumentet rriten, funksionet F 1 (t) dhe F 2 (-d) mbeten të kufizuar nga lart, kjo do të thotë që integralet e papërshtatshme përkatëse konvergojnë. Kjo është baza e teoremës së parë të krahasimit për integrale të funksioneve jonegative.

Lërini funksionet f(x) dhe g(x) në x?a të plotësojnë kushtet e mëposhtme:

• 1) 0?f(x)?g(x);
• 2) Funksionet f(x) dhe g(x) janë të vazhdueshme.

Pastaj nga konvergjenca e integralit vjen konvergjenca e integralit dhe nga divergjenca e integralit rrjedh divergjenca

Meqenëse 0?f(x)?g(x) dhe funksionet janë të vazhdueshme, atëherë

Sipas kushtit, integrali konvergon, d.m.th. ka një vlerë të fundme. Prandaj, integrali gjithashtu konvergon.

Tani le të ndryshojë integrali. Le të supozojmë se integrali konvergjon, por atëherë integrali duhet të konvergojë, gjë që bie në kundërshtim me kushtin. Supozimi ynë është i pasaktë, integrali ndryshon.

Teorema e krahasimit për integrale të parregullta të llojit të dytë.

Le të rritet për funksionet f(x) dhe g(x) në intervalin , pa kufi për x>+0. Për x>+0, pabarazia e mëposhtme vlen:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.

Teorema e krahasimit për integrale të parregullta të llojit të parë.

Le të jetë funksioni f(x) dhe g(x) në intervalin , dhe segmenti i integrimit është i fundëm, domethënë i kufizuar nga numrat dhe jo nga pafundësia. Disa detyra çojnë në nevojën për të braktisur këto kufizime. Kështu shfaqen integralet e pahijshme.

Kuptimi gjeometrik i integralit jo të duhur Rezulton mjaft thjesht. Në rastin kur grafiku i një funksioni y = f(x) është mbi bosht kau integrali i caktuar shpreh sipërfaqen e një trapezi lakor të kufizuar nga një kurbë y = f(x) , boshti x dhe ordinatat x = a , x = b. Nga ana tjetër, integrali i papërshtatshëm shpreh sipërfaqen e një trapezi lakor të pakufizuar (të pafund) të mbyllur midis vijave y = f(x) (në foton më poshtë - e kuqe), x = a dhe boshti i abshisave.

Integralet e pahijshme përcaktohen në mënyrë të ngjashme për intervalet e tjera të pafundme:

Sipërfaqja e një trapezi të lakuar të pafund mund të jetë një numër i fundëm, në këtë rast integrali i gabuar quhet konvergjent. Zona gjithashtu mund të jetë pafundësi, dhe në këtë rast integrali i gabuar quhet divergjent.

Përdorimi i kufirit të një integrali në vend të vetë integralit të papërshtatshëm. Për të vlerësuar integralin e papërshtatshëm, duhet të përdorni kufirin e integralit të caktuar. Nëse ky kufi ekziston dhe është i fundëm (jo i barabartë me pafundësinë), atëherë integrali i papërshtatshëm quhet konvergjent, dhe përndryshe - divergjent. Se çfarë priret një variabël nën shenjën e kufirit varet nëse kemi të bëjmë me një integral të papërshtatshëm të llojit të parë apo të llojit të dytë. Le të zbulojmë për këtë tani.

Integrale të pahijshme të llojit të parë - me kufij të pafund dhe konvergjencë të tyre

Integrale të pahijshme me kufi të sipërm të pafund

Pra, shkrimi i një integrali jo të duhur ndryshon nga integrali i zakonshëm i caktuar në atë që kufiri i sipërm i integrimit është i pafund.

Përkufizimi. Një integral i papërshtatshëm me një kufi të sipërm të pafund të integrimit të një funksioni të vazhdueshëm f(x) në intervalin nga a te ∞ quhet kufiri i integralit të këtij funksioni me kufirin e sipërm të integrimit b dhe kufiri i poshtëm i integrimit a me kusht që kufiri i sipërm i integrimit të rritet pa kufi, d.m.th.

.

Nëse ky kufi ekziston dhe është i barabartë me një numër dhe jo me pafundësi, atëherë një integral i gabuar quhet konvergjent, dhe si vlerë merret numri me të cilin kufiri është i barabartë. Përndryshe një integral i gabuar quhet divergjent dhe nuk i atribuohet asnjë kuptim.

Shembull 1. Llogaritni integralin jo të duhur(nëse konvergon).

Zgjidhje. Bazuar në përkufizimin e integralit jo të duhur, gjejmë

Meqenëse kufiri ekziston dhe është i barabartë me 1, atëherë kjo integral i papërshtatshëm konvergjon dhe është e barabartë me 1.

Në shembullin e mëposhtëm, integrani është pothuajse i njëjtë me shembullin 1, vetëm shkalla x nuk është dy, por shkronja alfa, dhe detyra është të studiohet integrali i papërshtatshëm për konvergjencë. Kjo do të thotë, pyetja mbetet për t'u përgjigjur: në cilat vlera të alfa konvergon ky integral i pahijshëm dhe në cilat vlera ndryshon?

Shembulli 2. Shqyrtoni integralin e papërshtatshëm për konvergjencë(kufiri i poshtëm i integrimit është më i madh se zero).

Zgjidhje. Së pari, le të supozojmë se, atëherë

Në shprehjen që rezulton, ne kalojmë në kufirin në:

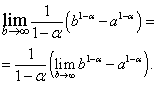
Është e lehtë të shihet se kufiri në anën e djathtë ekziston dhe është i barabartë me zero kur , domethënë dhe nuk ekziston kur , domethënë .

Në rastin e parë, pra kur . Nëse, atëherë dhe nuk ekziston.

Përfundimi i studimit tonë është si më poshtë: kjo integral i papërshtatshëm konvergjon në dhe divergon në .

Zbatimi i formulës Njuton-Leibniz për llojin e integralit jo të duhur që studiohet , mund të nxirrni formulën e mëposhtme, e cila është shumë e ngjashme me të:

.

Kjo është një formulë e përgjithësuar e Njuton-Leibniz.

Shembulli 3. Llogaritni integralin e gabuar(nëse konvergon).

Kufiri i këtij integrali ekziston:

Integrali i dytë, duke përbërë shumën që shpreh integralin origjinal:

Kufiri i këtij integrali ekziston gjithashtu:

.

Ne gjejmë shumën e dy integraleve, e cila është gjithashtu vlera e integralit të papërshtatshëm origjinal me dy kufij të pafundëm:

Integrale të pahijshme të llojit të dytë - nga funksionet e pakufizuara dhe konvergjenca e tyre

Lëreni funksionin f(x) dhënë në segmentin nga a te b dhe është e pakufizuar në të. Supozoni se funksioni shkon në pafundësi në pikë b , ndërsa në të gjitha pikat e tjera të segmentit është i vazhdueshëm.

Përkufizimi. Një integral jo i duhur i një funksioni f(x) në segmentin nga a te b quhet kufiri i integralit të këtij funksioni me kufirin e sipërm të integrimit c , nëse kur përpiqet c te b funksioni rritet pa kufi, dhe në pikë x = b funksioni nuk është përcaktuar, d.m.th.

.

Nëse ekziston ky kufi, atëherë integrali i papërshtatshëm i llojit të dytë quhet konvergjent, përndryshe quhet divergjent.

Duke përdorur formulën Newton-Leibniz, ne nxjerrim.

1. Integrale të papërshtatshme me kufij të pafund

Le të kujtojmë përkufizimin e një integrali si kufi i shumave integrale:

Përkufizimi supozon se intervali i integrimit është i fundëm dhe funksioni f(x) është i vazhdueshëm brenda tij. Shkelja e këtyre supozimeve çon në integrale të pahijshme.

Përkufizimi. Nëse integrali priret në një kufi të fundëm pasi rritet pafundësisht "b", atëherë ky kufi quhet një integral i papërshtatshëm me një kufi të sipërm të pafund të funksionit f (x) dhe shënohet me simbolin

Në këtë rast, integrali i papërshtatshëm thuhet se ekziston ose konvergohet.

Nëse kufiri i specifikuar nuk ekziston ose ekziston, por është i pafund, atëherë thuhet se integrali nuk ekziston ose divergjent.

Një integral i papërshtatshëm me një kufi të poshtëm të pafund përcaktohet në mënyrë të ngjashme:

Një integral i gabuar me dy kufij të pafund jepet nga:

ku c është çdo pikë fikse në boshtin Ox.

Pra, integralet e pahijshme mund të kenë një kufi të poshtëm të pafund, një kufi të sipërm të pafund, dhe gjithashtu dy kufij të pafund.

Shenjat e konvergjencës. Konvergjenca absolute dhe e kushtëzuar

Një integral ekziston vetëm nëse secili prej integraleve ekziston: dhe .

Shembull. Shqyrtoni konvergjencën e integralit

Duke supozuar c = 0, marrim:

ato. integrali konvergon.

Ndonjëherë nuk ka nevojë të llogaritet një integral jo i duhur, por mjafton vetëm të dimë nëse ai konvergon apo divergjent duke e krahasuar me një integral tjetër.

Teorema e krahasimit për integrale të parregullta.

Le të ketë funksioni f (x) në interval disa (numër të fundëm) pika ndërprerjeje të llojit të parë, kjo "pengesë" mund të eliminohet lehtësisht duke e ndarë segmentin në disa segmente me pika ndërprerjeje, duke llogaritur integrale të përcaktuara në çdo seksion individual dhe duke shtuar rezultatet.

Le të shqyrtojmë integralin e caktuar të një funksioni që është i pakufizuar kur i afrohemi njërit prej skajeve të segmentit, për shembull, .

(Në raste të tilla ata zakonisht thonë: "Funksioni ka një ndërprerje të pafundme në skajin e djathtë të intervalit të integrimit".)

Është e qartë se përkufizimi i zakonshëm i një integrali humbet kuptimin e tij këtu.

Përkufizimi. Një integral jo i duhur i funksionit f(x), i vazhdueshëm për një £ x< b и неограниченной при x ® b - 0, называется предел:

Integrali jo i duhur i një funksioni që ka një ndërprerje të pafundme në skajin e majtë të segmentit përcaktohet në mënyrë të ngjashme:

Rrjedhimisht, në seksionin [-1, 0] integrali ndryshon.

Kjo do të thotë që integrali ndryshon gjithashtu në seksion.

Kështu, ky integral divergjent gjatë gjithë intervalit [-1, 1]. Vini re se nëse do të fillonim të llogarisnim këtë integral pa i kushtuar vëmendje ndërprerjes së integrandit në pikën x = 0, do të merrnim një rezultat të pasaktë. Vërtet,

, gjë që është e pamundur.

Pra, për të studiuar integralin e papërshtatshëm të një funksioni të ndërprerë, është e nevojshme ta "ndani" atë në disa integrale dhe t'i studioni ato.

Nëse integrani ka një ndërprerje të llojit të dytë në intervalin (finit) të integrimit, flasim për një integral të papërshtatshëm të llojit të dytë.

10.2.1 Përkufizimi dhe vetitë themelore

Le të shënojmë intervalin e integrimit me $\left[ a, \, b \right ]$ që të dy këta numra supozohen të jenë të fundëm. Nëse ka vetëm 1 ndërprerje, ai mund të vendoset ose në pikën $a$, ose në pikën $b$, ose brenda intervalit $(a,\,b)$. Le të shqyrtojmë fillimisht rastin kur ka një ndërprerje të llojit të dytë në pikën $a$, dhe në pika të tjera funksioni integrand është i vazhdueshëm. Pra, ne po diskutojmë integralin

\fillimi(ekuacioni) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(ekuacioni)

dhe $f(x) \rightarrow \infty $ kur $x \rightarrow a+0$. Si më parë, gjëja e parë që duhet bërë është t'i jepni kuptim kësaj shprehjeje. Për ta bërë këtë, merrni parasysh integralin

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

Përkufizimi. Le të ketë një kufi të kufizuar

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

Pastaj thuhet se integrali i papërshtatshëm i llojit të dytë (22) konvergohet dhe vlera $A$ i caktohet atij vetë funksioni $f(x)$ thuhet se është i integrueshëm në intervalin $\left[a, \; , b\djathtas]$.

Le të shqyrtojmë opsionin kur ka një ndërprerje të llojit të dytë në funksionin integrand në kufirin e sipërm të intervalit të integrimit. Ky rast mund të reduktohet në atë të mëparshëm duke bërë ndryshimin e ndryshores $x=-t$ dhe më pas duke riorganizuar kufijtë e integrimit.

Le të shqyrtojmë opsionin kur funksioni integrand ka një ndërprerje të llojit të dytë brenda intervalit të integrimit, në pikën $c \in (a,\,b)$. Në këtë rast, integrali origjinal

\fillimi(ekuacioni) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(ekuacioni)

paraqitet si shumë

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Përkufizimi. Nëse të dy integralet $I_1, \, I_2$ konvergojnë, atëherë integrali i papërshtatshëm (23) quhet konvergjent dhe i caktohet një vlerë e barabartë me shumën e integraleve $I_1, \, I_2$, funksionin $f(x)$ quhet i integrueshëm në intervalin $\left [a, \, b\right]$. Nëse të paktën një nga integralet $I_1,\, I_2$ është divergjent, integrali i papërshtatshëm (23) quhet divergjent.

Integralet e parregullta konvergjente të llojit të dytë kanë të gjitha vetitë standarde të integraleve të zakonshëm të caktuar.

1. Nëse $f(x)$, $g(x)$ janë të integrueshme në intervalin $\left[ a, \,b \djathtas ]$, atëherë shuma e tyre $f(x)+g(x)$ është gjithashtu i integrueshëm në këtë interval, dhe \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Nëse $f(x)$ është i integrueshëm në intervalin $\left[ a, \, b \right ]$, atëherë për çdo konstante $C$ funksioni $C\cdot f(x)$ është gjithashtu i integrueshëm në këtë interval , dhe \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Nëse $f(x)$ është i integrueshëm në intervalin $\left[ a, \, b \right ]$, dhe në këtë interval $f(x)>0$, atëherë \[ \int _a^ (b ) f(x)dx\,>\,0. \] 4. Nëse $f(x)$ është i integrueshëm në intervalin $\left[ a, \, b \djathtas ]$, atëherë për çdo $c\in (a, \,b)$ integralet \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] gjithashtu konvergojnë, dhe \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (aditiviteti i integralit mbi intervalin).

Merrni parasysh integralin

\fillimi(ekuacioni) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \fund (ekuacion)

Nëse $k>0$, integrani priret në $\infty$ si $x \rightarrow +0$, kështu që integrali është i papërshtatshëm i llojit të dytë. Le të prezantojmë funksionin

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

Në këtë rast dihet antiderivati, pra

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

për $k \neq 1$,

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

për $k = 1$. Duke marrë parasysh sjelljen në $\epsilon \rightarrow +0$, arrijmë në përfundimin se integrali (20) konvergjon në $k

10.2.2 Testet për konvergjencën e integraleve jo të duhura të llojit të dytë

Teorema (shenja e parë e krahasimit). Le të jenë $f(x)$, $g(x)$ të vazhdueshme për $x\in (a,\,b)$ dhe $0 1. Nëse integrali \[ \int _a^(b)g(x) dx \] konvergjon, pastaj integrali \[ \int _a^(b)f(x)dx konvergjon. \] 2. Nëse integrali \[ \int _a^(b)f(x)dx \] divergon, atëherë integrali \[ \int _a^(b)g(x)dx divergon. \]

Teorema (kriteri i dytë i krahasimit). Le të jetë $f(x)$, $g(x)$ e vazhdueshme dhe pozitive për $x\in (a,\,b)$, dhe le të ketë një kufi të fundëm

\[ \theta = \lim_(x \djathtas shigjetë a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Pastaj integralet

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

konvergojnë ose ndryshojnë në të njëjtën kohë.