Çfarë është një ekuacion?

Ata që po hedhin hapat e tyre të parë në algjebër, sigurisht që kërkojnë prezantimin më të rregullt të materialit. Prandaj, në artikullin tonë se çfarë është një ekuacion, ne jo vetëm që do të japim një përkufizim, por gjithashtu do të japim klasifikime të ndryshme të ekuacioneve me shembuj.

Çfarë është një ekuacion: koncepte të përgjithshme

Pra, një ekuacion është një lloj barazie me një të panjohur, të shënuar me një shkronjë latine. Në këtë rast, vlera numerike e kësaj shkronje, e cila na lejon të marrim barazinë e saktë, quhet rrënja e ekuacionit. Më shumë për këtë mund të lexoni në artikullin tonë, por ne do të vazhdojmë të flasim për vetë ekuacionet. Argumentet e një ekuacioni (ose variablave) janë të panjohura, dhe zgjidhja e një ekuacioni është gjetja e të gjitha rrënjëve të tij ose mungesa e rrënjëve.

Llojet e ekuacioneve

Ekuacionet ndahen në dy grupe të mëdha: algjebrike dhe transcendentale.

• Një ekuacion algjebrik është ai në të cilin përdoren vetëm operacionet algjebrike për të gjetur rrënjën e ekuacionit - 4 ato aritmetike, si dhe për përcaktimin dhe nxjerrjen e rrënjës natyrore.
• Një ekuacion transcendental është një ekuacion në të cilin funksionet joalgjebrike përdoren për të gjetur rrënjën: për shembull, trigonometrike, logaritmike dhe të tjera.

Ndër ekuacionet algjebrike ka edhe:

• numra të plotë - me të dyja pjesët që përbëhen nga shprehje të tëra algjebrike në lidhje me të panjohurat;
• thyesore - që përmban shprehje algjebrike me numra të plotë në numërues dhe emërues;
• irracionale - shprehjet algjebrike këtu janë nën shenjën e rrënjës.

Vini re gjithashtu se ekuacionet fraksionale dhe irracionale mund të reduktohen në zgjidhjen e ekuacioneve të tëra.

Ekuacionet transcendentale ndahen në:

• Ekuacionet eksponenciale janë ekuacione që përmbajnë një ndryshore si eksponent. Ato zgjidhen duke lëvizur në një bazë ose eksponent të vetëm, duke nxjerrë nga kllapat faktorin e përbashkët, faktorizimin dhe disa metoda të tjera;
• logaritmike - ekuacione me logaritme, pra ekuacione ku të panjohurat janë brenda vetë logaritmeve. Zgjidhja e ekuacioneve të tilla është shumë e vështirë (ndryshe nga, të themi, shumica e atyre algjebrike), pasi kjo kërkon trajnim të fortë matematikor. Gjëja më e rëndësishme këtu është të kalojmë nga një ekuacion me logaritme në një ekuacion pa to, domethënë të thjeshtojmë ekuacionin (kjo metodë e heqjes së logaritmeve quhet fuqizim). Natyrisht, është e mundur të fuqizohet një ekuacion logaritmik vetëm nëse ato kanë baza numerike identike dhe nuk kanë koeficientë;
• ekuacionet trigonometrike janë ekuacione me variabla nën shenjat e funksioneve trigonometrike. Zgjidhja e tyre kërkon zotërim fillestar të funksioneve trigonometrike;
• të përziera janë ekuacionet e diferencuara me pjesë që u përkasin llojeve të ndryshme (për shembull, me pjesë parabolike dhe eliptike ose eliptike dhe hiperbolike, etj.).

Sa i përket klasifikimit sipas numrit të të panjohurave, gjithçka është e thjeshtë: dallohen ekuacionet me një, dy, tre, e kështu me radhë të panjohura. Ekziston edhe një klasifikim tjetër, i cili bazohet në shkallën që është në anën e majtë të polinomit. Në bazë të kësaj dallohen ekuacionet lineare, kuadratike dhe kubike. Ekuacionet lineare mund të quhen gjithashtu ekuacione të shkallës 1, kuadratike - 2, dhe kubike, përkatësisht, 3. Epo, tani le të japim shembuj të ekuacioneve të një grupi ose një tjetër.

Shembuj të llojeve të ndryshme të ekuacioneve

Shembuj të ekuacioneve algjebrike:

• sëpatë + b= 0
• sëpatë 3 + bx 2 + cx+ d= 0
• sëpatë 4 + bx 3 + cx 2 + bx + a= 0
  (a nuk është e barabartë me 0)

Shembuj të ekuacioneve transcendentale:

• cos x = x log x = x−5 2 x = logx+x 5 +40

Shembuj të ekuacioneve të plota:

• (2+x)2 = (2+x)(55x-4) (x2-12x+10)4 = (3x+10)4 (4x2+3x-10)2=9x4

Shembull i ekuacioneve thyesore:

• 15 x + — = 5x - 17 x

Shembull i ekuacioneve irracionale:

• √2kf(x)=g(x)

Shembuj të ekuacioneve lineare:

• 2x+7=0 x - 3 = 2 - 4x 2x+3=5x+5 - 3x - 2

Shembuj të ekuacioneve kuadratike:

• x 2 +5x−7= 0 3x 2 +5x−7= 0 11x 2 −7x+3 = 0

Shembuj të ekuacioneve kubike:

• x 3 -9x 2 -46x+120=0 x 3 - 4x 2 + x + 6 = 0

Shembuj të ekuacioneve eksponenciale:

• 5 x+2 = 125 3 x 2 x = 8 x+3 3 2x +4 3 x -5 = 0

Shembuj të ekuacioneve logaritmike:

• log 2 x= 3 log 3 x= -1

Shembuj të ekuacioneve trigonometrike:

• 3sin 2 x + 4sin x cosx + cos 2 x = 2 sin(5x+π/4) = ctg(2x-π/3) sinx + cos 2 x + tan 3 x = ctg 4 x

Shembuj të ekuacioneve të përziera:

• log x (log 9 (4⋅3 x −3))=1 |5x−8|+|2⋅5x+3|=13

Mbetet për të shtuar se një sërë metodash përdoren për të zgjidhur ekuacione të llojeve të ndryshme. Epo, për të zgjidhur pothuajse çdo ekuacion, do t'ju duhet njohuri jo vetëm për algjebrën, por edhe për trigonometrinë, dhe shpesh njohuri shumë të thella.

Matematika. Algjebër. Gjeometria. Trigonometria

ALGEBRA: Ekuacionet dhe sistemet e ekuacioneve

4.2. Llojet e ekuacioneve dhe metodat për zgjidhjen e tyre

Në rastin kur është e nevojshme të gjenden vlerat e një ndryshoreje që plotësojnë të dy ekuacionet e dhëna, themi se është dhënë, sistemi i ekuacioneve. Një mbajtës kaçurrelë përdoret për të treguar një sistem:

Disa ekuacione me një formë të ndryshueshme grup ekuacionesh, nëse detyra është të gjejmë të gjitha vlerat e tilla të një ndryshoreje, secila prej të cilave është rrënja e të paktën një prej këtyre ekuacioneve. Një kllapa katrore përdoret për të treguar një popullsi:

Ekuacionet që përmbajnë një ndryshore nën shenjën e modulit.

Vlera absolute e një numri A përkufizohet si më poshtë:

Shembull: Zgjidheni ekuacionin

.

Zgjidhja: Nëse

, Kjo . Mund ta shkruani kështu:

Nga barazimi.

ne gjejme X= -9. Megjithatë, me këtë vlerë të ndryshores, pabarazia nuk qëndron, që do të thotë se vlera e gjetur nuk është rrënja e këtij ekuacioni., Kjo dhe ky ekuacion do të marrë formën. Mund ta shkruani kështu:

Nga barazimi.

ne gjejme . Pabarazia është e vërtetë, që do të thotë - rrënja e këtij ekuacioni..

Ekuacionet me një ndryshore në emërues.

Merrni parasysh ekuacionet e formës

. (1)

Zgjidhja e një ekuacioni të tipit (1) bazohet në pohimin e mëposhtëm: një thyesë është e barabartë me 0 nëse dhe vetëm nëse numëruesi i saj është i barabartë me 0 dhe emëruesi i tij është jo zero.

Në përputhje me sa më sipër, zgjidhja e ekuacionit

kryhet në dy faza: së pari ju duhet të zgjidhni ekuacionin, dhe më pas zbuloni nëse, me vlerat e gjetura të ndryshores, X emërues në 0. Nëse q(x) ¹ 0 , pastaj rrënja e gjetur e ekuacionitështë gjithashtu rrënja e ekuacionit (1); Nëseq(x) = 0, pastaj rrënja rezultuese e ekuacionitështë gjithashtu rrënja e ekuacionit (1). Sistemi që rezulton është:

Domeni i ekuacionit

f(x) = g(x) thirrni grupin e të gjitha atyre vlerave të një ndryshoreje X, për të cilën shprehjaf(x), dhe shprehja g(x)ka kuptim.

Nëse në procesin e transformimit të një ekuacioni domeni i përkufizimit të tij është zgjeruar, atëherë mund të shfaqen rrënjë të jashtme. Prandaj, të gjitha vlerat e gjetura të ndryshores duhet të kontrollohen duke zëvendësuar në ekuacionin origjinal ose duke përdorur domenin e përkufizimit të ekuacionit origjinal.

Ekuacionet racionale.

Ekuacioni

f(x) = g(x) thirrur racionale, Nëse f(x) dhe g(x)-shprehje racionale. Për më tepër, nëse f(x) dhe g(x)- shprehje të tëra, atëherë thirret ekuacioni e tërë ;nëse të paktën një nga shprehjetf(x), g(x)është thyesore, atëherë ekuacioni racionalf(x) = g(x) thirrur thyesore .

Për të zgjidhur një ekuacion racional, ju duhet:

1. gjeni emëruesin e përbashkët të të gjitha thyesave të disponueshme;
2. zëvendësoni këtë ekuacion me një të plotë, duke shumëzuar të dyja pjesët e tij me një emërues të përbashkët;
3. Të zgjidhë ekuacionin e plotë që rezulton;
4. Zhduk nga rrënjët ato që e bëjnë të zhduket emëruesi i përbashkët.

Zgjidhja e ekuacionit

p(x) = 0 metoda e faktorizimit. p(x) mund të faktorizohet: , pastaj ekuacioni merr formën . Nëse A- rrënja e ekuacionit, Kjo , pra të paktën një nga numratështë e barabartë me 0.

E kundërta është gjithashtu e vërtetë: nëse X

= A- rrënja e të paktën një prej ekuacioneve, , , Kjo A- rrënja e ekuacionit. Kjo eshte

Zgjidhja e ekuacioneve

duke futur një ndryshore të re.

Le të shpjegojmë thelbin e metodës me një shembull.

Shembull: Zgjidheni ekuacionin

.

Zgjidhja Le të vendosim

, marrim ekuacionin, ku gjejmë . Problemi zbret në zgjidhjen e një grupi ekuacionesh

Û

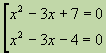
Ekuacioni i parë kuadratik nuk ka rrënjë reale, kështu që diskriminuesi i tij është negativ. Nga e dyta gjejmë

. Këto janë rrënjët e ekuacionit të dhënë.

Një ekuacion i formës quhet bikuadratik

, Ku A ¹ 0. Ekuacioni bikuadratik zgjidhet duke futur një ndryshore të re: duke vënë , arrijmë në ekuacionin kuadratik .

Ekuacionet irracionale.

Irracionale

Quhet një ekuacion në të cilin ndryshorja gjendet nën shenjën e rrënjës ose nën shenjën e ngritjes në një fuqi thyesore. Një metodë për zgjidhjen e ekuacioneve të tilla është metoda e ngritjes së të dy anëve të ekuacionit në të njëjtën fuqi:

A) transformojnë ekuacionin e dhënë irracional në formë:

;

B) ngremë të dyja anët e ekuacionit që rezulton në

n shkalla e -të:

;

B) duke pasur parasysh se

, marrim ekuacionin

f(x) = g(x);

)Ne e zgjidhim ekuacionin dhe bëjmë një kontroll, pasi ngritja e të dy anëve të ekuacionit në një fuqi të barabartë mund të çojë në shfaqjen e rrënjëve të jashtme. Ky kontroll kryhet duke zëvendësuar vlerat e gjetura të ndryshores në ekuacionin origjinal.

E drejta e autorit © 2005-2013 Xenoid v2.0

Përdorimi i materialeve të faqes është i mundur në varësi të një lidhjeje aktive.

Ruajtja e privatësisë suaj është e rëndësishme për ne. Për këtë arsye, ne kemi zhvilluar një politikë të privatësisë që përshkruan se si ne përdorim dhe ruajmë informacionin tuaj. Ju lutemi rishikoni praktikat tona të privatësisë dhe na tregoni nëse keni ndonjë pyetje.

Mbledhja dhe përdorimi i informacionit personal

Informacioni personal i referohet të dhënave që mund të përdoren për të identifikuar ose kontaktuar një person specifik.

Mund t'ju kërkohet të jepni informacionin tuaj personal në çdo kohë kur na kontaktoni.

Më poshtë janë disa shembuj të llojeve të informacionit personal që mund të mbledhim dhe se si mund ta përdorim këtë informacion.

Çfarë informacioni personal mbledhim:

• Kur dorëzoni një aplikim në sajt, ne mund të mbledhim informacione të ndryshme, duke përfshirë emrin tuaj, numrin e telefonit, adresën e emailit, etj.

Si i përdorim të dhënat tuaja personale:

• Informacioni personal që mbledhim na lejon t'ju kontaktojmë me oferta unike, promovime dhe ngjarje të tjera dhe ngjarje të ardhshme.
• Herë pas here, ne mund të përdorim të dhënat tuaja personale për të dërguar njoftime dhe komunikime të rëndësishme.
• Ne gjithashtu mund të përdorim të dhënat personale për qëllime të brendshme, si kryerja e auditimeve, analizave të të dhënave dhe kërkimeve të ndryshme, me qëllim që të përmirësojmë shërbimet që ofrojmë dhe t'ju ofrojmë rekomandime në lidhje me shërbimet tona.
• Nëse merrni pjesë në një tërheqje çmimesh, konkurs ose promovim të ngjashëm, ne mund të përdorim informacionin që ju jepni për të administruar programe të tilla.

Zbulimi i informacionit palëve të treta

Ne nuk ua zbulojmë informacionin e marrë nga ju palëve të treta.

Përjashtimet:

• Nëse është e nevojshme - në përputhje me ligjin, procedurën gjyqësore, në procedurat ligjore dhe/ose në bazë të kërkesave publike ose kërkesave nga organet qeveritare në Federatën Ruse - për të zbuluar informacionin tuaj personal. Ne gjithashtu mund të zbulojmë informacione për ju nëse përcaktojmë se një zbulim i tillë është i nevojshëm ose i përshtatshëm për qëllime sigurie, zbatimi të ligjit ose qëllime të tjera me rëndësi publike.
• Në rast të një riorganizimi, bashkimi ose shitjeje, ne mund t'i transferojmë informacionet personale që mbledhim te pala e tretë pasardhëse e aplikueshme.

Mbrojtja e informacionit personal

Ne marrim masa paraprake - duke përfshirë administrative, teknike dhe fizike - për të mbrojtur informacionin tuaj personal nga humbja, vjedhja dhe keqpërdorimi, si dhe qasja, zbulimi, ndryshimi dhe shkatërrimi i paautorizuar.

Respektimi i privatësisë suaj në nivel kompanie

Për t'u siguruar që informacioni juaj personal është i sigurt, ne i komunikojmë punonjësve tanë standardet e privatësisë dhe sigurisë dhe zbatojmë në mënyrë rigoroze praktikat e privatësisë.

Llojet e ekuacioneve algjebrike dhe metodat për zgjidhjen e tyre

Për studentët e interesuar në matematikë, kur zgjidhin ekuacione algjebrike të shkallëve më të larta, një metodë efektive për gjetjen e shpejtë të rrënjëve, pjesëtimi me një mbetje me binomin x -  ose me bosht + b, është skema Horner.

Merrni parasysh skemën e Hornerit.

Le të shënojmë herësin jo të plotë kur pjesëtojmë P(x) me x –  përmes

Q (x) = b 0 x n -1 + b 1 x n -2 + ... + b n -1, dhe pjesa e mbetur është b n.

Meqenëse P(x) = Q (x)(x–) + b n, atëherë barazia vlen

a 0 x n + а 1 x n -1 + … + а n = (b 0 x n -1 + b 1 x n -2 + … + b n -1)(х–) + b n

Le të hapim kllapat në anën e djathtë dhe të krahasojmë koeficientët për të njëjtat fuqi të x në të majtë dhe në të djathtë. Përftojmë se a 0 = b 0 dhe për 1  k  n vlejnë marrëdhëniet a k = b k -  b k -1. Nga kjo rrjedh se b 0 = a 0 dhe b k = a k +  b k -1, 1  k  n.

Llogaritjen e koeficientëve të polinomit Q (x) dhe mbetjes b n e shkruajmë në formën e tabelës:

a 0

a 1

a 2

A n-1

A n

b 0 = a 0

b 1 = a 1 +  b 0

b 2 = a 2 +  b 1

b n-1 = a n-1 +  b n-2

b n = a n +  b n-1

Shembulli 1. Ndajeni polinomin 2x 4 – 7x 3 – 3x 2 + 5x – 1 me x + 1.

Zgjidhje. Ne përdorim skemën e Horner.

Kur pjesëtojmë 2x 4 – 7x 3 – 3x 2 + 5x – 1 me x + 1 marrim 2x 3 – 9x 2 + 6x – 1

Përgjigje: 2 x 3 – 9x 2 + 6x – 1

Shembulli 2. Llogaritni P(3), ku P(x) = 4x 5 – 7x 4 + 5x 3 – 2x + 1

Zgjidhje. Duke përdorur teoremën e Bezout dhe skemën e Hornerit, marrim:

Përgjigje: P(3) = 535

Ushtrimi

Duke përdorur diagramin e Hornerit, ndani polinomin

4x 3 – x 5 + 132 – 8x 2 në x + 2;

2) Ndani polinomin

2x 2 – 3x 3 – x + x 5 + 1 në x + 1;

3) Gjeni vlerën e polinomit P 5 (x) = 2x 5 – 4x 4 – x 2 + 1 për x = 7.

1.1. Gjetja e rrënjëve racionale të ekuacioneve me koeficientë të plotë

Metoda për gjetjen e rrënjëve racionale të një ekuacioni algjebrik me koeficientë të plotë është dhënë nga teorema e mëposhtme.

Teorema: Nëse një ekuacion me koeficientë të plotë ka rrënjë racionale, atëherë ato janë herësi i pjesëtimit të pjesëtuesit të termit të lirë me pjesëtuesin e koeficientit kryesor.

Dëshmi: a 0 x n + a 1 x n -1 + … + a n = 0

Le të x = p/ q është një rrënjë racionale, q, p janë të dyfishta.

Duke zëvendësuar thyesën p/q në ekuacion dhe duke u çliruar nga emëruesi, marrim

a 0 r n + a 1 p n -1 q + … + a n -1 pq n -1 + a n q n = 0 (1)

Le të rishkruajmë (1) në dy mënyra:

a n q n = р(– а 0 р n -1 – а 1 р n -2 q – … – а n -1 q n -1) (2)

a 0 r n = q (– а 1 р n -1 –… – а n -1 рq n -2 – а n q n -1) (3)

Nga barazia (2) del se a n q n pjesëtohet me p, dhe meqë q n dhe p janë të dyfishta, atëherë a n pjesëtohet me p. Në mënyrë të ngjashme, nga barazia (3) rezulton se një 0 pjesëtohet me q. Teorema është vërtetuar.

Shembulli 1. Zgjidhet ekuacioni 2x 3 – 7x 2 + 5x – 1 = 0.

Zgjidhje. Ekuacioni nuk ka rrënjë të plota; ne gjejmë rrënjët racionale të ekuacionit. Le të jetë rrënja e ekuacionit thyesa e pakalueshme p /q, atëherë p gjendet midis pjesëtuesve të termit të lirë, d.m.th. midis numrave  1, dhe q midis pjesëtuesve pozitivë të koeficientit kryesor: 1; 2.

Ato. rrënjët racionale të ekuacionit duhet të kërkohen midis numrave  1,  1/2, shënoni P 3 (x) = 2x 3 – 7x 2 + 5x – 1, P 3 (1)  0, P 3 (–1)  0,

P 3 (1/2) = 2/8 – 7/4 + 5/2 – 1 = 0, 1/2 është rrënja e ekuacionit.

2x 3 – 7x 2 + 5x – 1 = 2x 3 – x 2 – 6 x 2 + 3x + 2x – 1 = 0.

Ne marrim: x 2 (2x – 1) – 3x (2x – 1)+ (2x – 1) = 0; (2x – 1) (x 2 – 3x + 1) = 0.

Duke barazuar faktorin e dytë me zero dhe duke zgjidhur ekuacionin, marrim

Përgjigje:
,

Ushtrime

Zgjidh ekuacionet:

6x 3 – 25x 2 + 3x + 4 = 0;

6x 4 – 7x 3 – 6x 2 + 2x + 1 = 0;

3x 4 – 8x 3 – 2x 2 + 7x – 1 = 0;

1.2. Ekuacionet reciproke dhe metodat e zgjidhjes

Përkufizimi. Një ekuacion me fuqi të plotë në lidhje me një të panjohur quhet i përsëritur nëse koeficientët e tij, të barabartë nga skajet e anës së majtë, janë të barabartë me njëri-tjetrin, d.m.th. ekuacioni i formës

A x n + bx n -1 + cx n -2 + … + cx 2 + bx + a = 0

Ekuacioni reciprok i shkallës tek

A x 2 n +1 + bx 2 n + cx 2 n -1 + … + cx 2 + bx + a = 0

ka gjithmonë një rrënjë x = – 1. Prandaj, është ekuivalente me kombinimin e ekuacionit x + 1 = 0 dhe  x 2 n +  x 2 n -1 + … +  x +  = 0. Ekuacioni i fundit është një ekuacion reciprok të shkallës çift. Kështu, zgjidhja e ekuacioneve reciproke të çdo shkalle reduktohet në zgjidhjen e një ekuacioni reciprok të shkallës çift.

Si ta zgjidhim atë? Le të jepet një ekuacion reciprok me shkallë çift

A x 2 n + bx 2 n -1 + … + dx n +1 + ex n + dx n -1 + … + bx + a = 0

Vini re se x = 0 nuk është një rrënjë e ekuacionit. Pastaj e ndajmë ekuacionin me x n, marrim

A x n + bx n -1 + … + dx + e + dx -1 + … + bx 1- n + аx -n = 0

I grupojmë në dyshe termat e anës së majtë

A( x n + x - n ) + b (x n -1 + x -(n -1) + … + d(x + x -1 ) + e = 0

Bëjmë zëvendësimin x + x -1 = y. Pas zëvendësimit të shprehjeve x 2 + x -2 = y 2 – 2;

x 3 + x -3 = y 3 – 3y; x 4 + x -4 = y 4 – 4y + 2 në ekuacion marrim ekuacionin për nëАу n + Nga n -1 +Cy n -2 + … + Ey + D = 0.

Për të zgjidhur këtë ekuacion, duhet të zgjidhni disa ekuacione kuadratike të formës x + x -1 = y k, ku k = 1, 2, ... n. Kështu, marrim rrënjët e ekuacionit origjinal.

Shembulli 1. Zgjidhet ekuacioni x 7 + x 6 – 5x 5 – 13x 4 – 13x 3 – 5x 2 + 2x + 1 = 0.

Zgjidhje. x = – 1 është rrënja e ekuacionit. Le të zbatojmë skemën e Hornerit.

Ekuacioni ynë do të marrë formën:

(x + 1) (x 6 + x 5 - 6x 4 - 7x 3 - 6x 2 + x + 1) = 0

1) x + 1 = 0, x = -1;

2) x 6 + x 5 – 6x 4 – 7x 3 – 6x 2 + x + 1 = 0 | : x 3  0; x 3 + x 2 – 6x – 7 – 6/x + 1/x 2 + 1/x 3 =0.

Duke grupuar, marrim: .

Le të prezantojmë një zëvendësim:
;
;
.

Ne marrim relativisht në ekuacioni: y 3 – 3y + y 2 – 2 – 6y – 7 = 0;

y 3 + y 2 – 9y – 9 = 0; y 2 (y + 1) – 9 (y + 1) = 0; (y + 1) (y 2 – 9); y 1 = -1, y 2,3 =  3.

Zgjidhja e ekuacioneve
,
,
,

marrim rrënjët:
,
,
,

Përgjigje: x 1 = -1,
,

Ushtrime

Zgjidh ekuacione.

2x 5 + 5x 4 – 13x 3 – 13x 2 + 5x + 2 = 0;

2x 4 + 3x 3 – 16x 2 + 3x + 2 = 0;

15x 5 + 34x 4 + 15x 3 – 15x 2 – 34x – 15 = 0.

1.3. Metoda e zëvendësimit të ndryshoreve për zgjidhjen e ekuacioneve

Metoda e zëvendësimit të variablave është metoda më e zakonshme. Arti për të bërë një ndryshim të ndryshueshëm është të shohësh se cili ndryshim ka më shumë kuptim dhe do të çojë në sukses më shpejt.

Nëse jepet ekuacioni

F(f(x)) = 0, (1)

atëherë duke e zëvendësuar të panjohurën y = f (x) fillimisht reduktohet në ekuacion

F(y) = 0, (2)

dhe pastaj pas gjetjes së të gjitha zgjidhjeve të ekuacionit (2) y 1, y 2, ..., y n, ... reduktohet në zgjidhjen e grupit të ekuacioneve f (x) = y 1, f (x) = y 2 ,..., f (x) = y 2,...

Mënyrat kryesore për të zbatuar metodën e zëvendësimit të variablave janë:

duke përdorur vetinë bazë të një thyese;

nxjerrja në pah e katrorit të binomit;

kalimi në një sistem ekuacionesh;

kllapa hapëse në çifte;

hapja e kllapave në dyshe dhe pjesëtimi i të dy anëve të ekuacionit;

zvogëlimi i shkallës së ekuacionit;

zëvendësim i dyfishtë.

1.3.1. Zvogëlimi i fuqisë së një ekuacioni

Zgjidheni ekuacionin (x 2 + x + 2) (x 2 + x + 3) = 6 (3)

Zgjidhje. Le të shënojmë x 2 + x + 2 = y, pastaj le të marrim y (y + 1) = 6, duke zgjidhur këtë të fundit, marrim y 1 = 2, y 2 = -3. Ky ekuacion (3) është ekuivalent me bashkësinë e ekuacioneve x 2 + x + 2 = 2

x 2 + x + 2 = -3

Duke zgjidhur të parën, marrim x 1 = 0, x 2 = -1. Duke zgjidhur të dytën, marrim
,

Përgjigje: x 1 = 0, x 2 = -1,

1.3.2. Ekuacioni i shkallës së katërt të formës (x + a)(x +b )(x + c )(x + d ) = m , ku a + b = c + d, ose a + c = b + d, ose a + d = b + c.

Shembull. Zgjidhe ekuacionin (x - 1)(x - 7)(x -4)(x + 2) = 40

Zgjidhje. – 1- 4 = - 7 + 2, - 5 = - 5, duke shumëzuar këto çifte kllapash, marrim ekuacionin (x 2 - 5x - 14) (x 2 - 5x + 4) = 40

Le të prezantojmë zëvendësimin: x 2 - 5x – 14 = y, marrim ekuacionin y(y + 18) = 40, y 2 + 18y = 40, y 2 + 18y – 40 = 0. y 1 = -20, y 2 = 2. Duke u kthyer te ndryshorja origjinale, zgjidhim një grup ekuacionesh:

X 2 - 5x – 14 = - 20 x 1 = 2; x 2 = 3

x 2 - 5x – 14 = 2 x 3,4 =

Përgjigje: x 1 = 2; x 2 = 3 x 3,4 =

1.3.3. Një ekuacion i formës (x + a) (x + b) (x + c) (x + d) = Shemb 2,

Ku ab = cd, ose ac =bd, ose ad = bc. Hapni kllapat në dyshe dhe ndani të dyja pjesët me x 2  0.

Shembull. (x - 1)(x - 2)(x - 8)(x - 4) = 4x 2

Zgjidhje. Prodhimi i numrave në kllapat e parë dhe të tretë dhe në kllapat e dytë dhe të katërt janë të barabartë, d.m.th. – 8 (- 1) = (- 2)(- 4). Le të shumëzojmë çiftet e treguara të kllapave dhe të shkruajmë ekuacionin (x 2 - 9x + 8) (x 2 - 6x + 8) = 4x 2.

Meqenëse x = 0 nuk është një rrënjë e ekuacionit, ne i ndajmë të dy anët e ekuacionit me x 2  0, marrim:
, zëvendësim:
, ekuacioni origjinal do të marrë formën:t(t+3) =4, t 2 + 3 t=4, t 2 + 3 t – 4=0, t 1 =1, t 2 = - 4.

Le të kthehemi te ndryshorja origjinale:

x 2 - 10x + 8 = 0

x 2 - 5x + 8 = 0

Zgjidhim ekuacionin e parë, marrim x 1,2 = 5 

Ekuacioni i dytë nuk ka rrënjë.

Përgjigje: x 1.2 = 5 

1.3.4. Ekuacioni i tipit të katërt (ax 2 + b 1 x + c)(a x 2 + b 2 x + c) = A x 2

Ekuacioni (sëpatë 2 + b 1 x+ c)(a x 2 + b 2 x + c) = A x 2, ku c  0, A  2
, i cili pasi zëvendësoi të panjohurën
mund të rishkruhet si katror dhe mund të zgjidhet lehtësisht.

Shembull. (x 2 + x+ 2) (x 2 + 2x + 2) = 2x 2

Zgjidhje. Është e lehtë të shihet se x = 0 nuk është një rrënjë e këtij ekuacioni duke e ndarë këtë ekuacion me x 2 , marrim ekuacionin

zëvendësim
, marrim ekuacionin (y+1)(y+2) = 2, duke e zgjidhur, kemi rrënjët y 1 = 0; në 2 = - 3, prandaj ekuacioni origjinal është i barabartë me bashkësinë e ekuacioneve

duke zgjidhur, marrim x 1 = -1; x 2 = -2.

Përgjigje: x 1 = -1; x 2 = -2

1.3.5. Ekuacioni i formës: a (cx 2 + p 1 x + q) 2 + b (cx 2 + p 2 x + q) 2 = Ax 2

Ekuacioni a(cx 2 + fq 1 x + q) 2 + b(cx 2 + fq 2 x + q) 2 = Sëpatë 2 ku a, b, c, q, A janë të tilla që q 0, A 0, c 0, a 0, b 0 nuk ka rrënjë x = 0, pra pjesëtimi i ekuacionit me x 2 , marrim një ekuacion ekuivalent
, e cila pas zëvendësimit
mund të rishkruhet si një ekuacion kuadratik që mund të zgjidhet lehtësisht. + 1)( x 2 – 14x + 15 = 0

x 2 – 7 x + 15 = 0

Përgjigje:

Në disa probleme të fizikës, nuk është e mundur të vendoset një lidhje e drejtpërdrejtë midis sasive që përshkruajnë procesin. Por është e mundur të merret një barazi që përmban derivatet e funksioneve në studim. Kështu lindin ekuacionet diferenciale dhe nevoja për t'i zgjidhur ato për të gjetur një funksion të panjohur.

Ky artikull është menduar për ata që përballen me problemin e zgjidhjes së një ekuacioni diferencial në të cilin funksioni i panjohur është funksion i një ndryshoreje. Teoria është e strukturuar në atë mënyrë që me njohuri zero të ekuacioneve diferenciale, të mund të përballeni me detyrën tuaj.

Çdo lloj ekuacioni diferencial shoqërohet me një metodë zgjidhjeje me shpjegime të hollësishme dhe zgjidhje për shembuj dhe probleme tipike. E tëra çfarë ju duhet të bëni është të përcaktoni llojin e ekuacionit diferencial të problemit tuaj, të gjeni një shembull të ngjashëm të analizuar dhe të kryeni veprime të ngjashme.

Për të zgjidhur me sukses ekuacionet diferenciale, do t'ju duhet gjithashtu aftësia për të gjetur grupe antiderivativësh (integrale të pacaktuar) të funksioneve të ndryshme. Nëse është e nevojshme, ju rekomandojmë t'i referoheni seksionit.

Së pari, ne do të shqyrtojmë llojet e ekuacioneve diferenciale të zakonshme të rendit të parë që mund të zgjidhen në lidhje me derivatin, më pas do të kalojmë në ODE të rendit të dytë, pastaj do të ndalemi në ekuacionet e rendit më të lartë dhe do të përfundojmë me sistemet e ekuacionet diferenciale.

Kujtojmë se nëse y është funksion i argumentit x.

Ekuacionet diferenciale të rendit të parë.

Ekuacionet diferenciale më të thjeshta të rendit të parë të formës.

Le të shkruajmë disa shembuj të telekomandës së tillë .

Ekuacionet diferenciale mund të zgjidhet në lidhje me derivatin duke pjesëtuar të dyja anët e barazisë me f(x) . Në këtë rast, arrijmë në një ekuacion që do të jetë ekuivalent me atë origjinal për f(x) ≠ 0. Shembuj të ODE-ve të tilla janë .

Nëse ka vlera të argumentit x në të cilat funksionet f(x) dhe g(x) zhduken njëkohësisht, atëherë shfaqen zgjidhje shtesë. Zgjidhje shtesë të ekuacionit dhënë x janë çdo funksion të përcaktuar për këto vlera argumentesh. Shembuj të ekuacioneve të tilla diferenciale përfshijnë:

Ekuacionet diferenciale të rendit të dytë.

Ekuacione diferenciale homogjene lineare të rendit të dytë me koeficientë konstante.

LDE me koeficientë konstante është një lloj shumë i zakonshëm i ekuacionit diferencial. Zgjidhja e tyre nuk është veçanërisht e vështirë. Së pari, gjenden rrënjët e ekuacionit karakteristik . Për p dhe q të ndryshme, tre raste janë të mundshme: rrënjët e ekuacionit karakteristik mund të jenë reale dhe të ndryshme, reale dhe përkuese. ose konjugate komplekse. Në varësi të vlerave të rrënjëve të ekuacionit karakteristik, zgjidhja e përgjithshme e ekuacionit diferencial shkruhet si , ose , ose përkatësisht.

Për shembull, merrni parasysh një ekuacion linear homogjen diferencial të rendit të dytë me koeficientë konstante. Rrënjët e ekuacionit të tij karakteristik janë k 1 = -3 dhe k 2 = 0. Rrënjët janë reale dhe të ndryshme, prandaj zgjidhja e përgjithshme e LODE me koeficientë konstante ka formën


Ekuacione diferenciale johomogjene lineare të rendit të dytë me koeficientë konstante.

Zgjidhja e përgjithshme e një LDDE të rendit të dytë me koeficientë konstante y kërkohet në formën e shumës së zgjidhjes së përgjithshme të LDDE përkatëse. dhe një zgjidhje të veçantë për ekuacionin origjinal johomogjen, që është, . Paragrafi i mëparshëm i kushtohet gjetjes së një zgjidhjeje të përgjithshme për një ekuacion diferencial homogjen me koeficientë konstante. Dhe një zgjidhje e veçantë përcaktohet ose me metodën e koeficientëve të pacaktuar për një formë të caktuar të funksionit f(x) në anën e djathtë të ekuacionit origjinal, ose me metodën e ndryshimit të konstantave arbitrare.

Si shembuj të LDDE-ve të rendit të dytë me koeficientë konstante, ne japim


Për të kuptuar teorinë dhe për t'u njohur me zgjidhjet e hollësishme të shembujve, ne ju ofrojmë në faqe ekuacione diferenciale lineare johomogjene të rendit të dytë me koeficientë konstante.

Ekuacionet lineare homogjene diferenciale (LODE) dhe ekuacionet diferenciale johomogjene lineare (LNDEs) të rendit të dytë.

Një rast i veçantë i ekuacioneve diferenciale të këtij lloji janë LODE dhe LDDE me koeficientë konstante.

Zgjidhja e përgjithshme e LODE në një segment të caktuar përfaqësohet nga një kombinim linear i dy zgjidhjeve të pjesshme lineare të pavarura y 1 dhe y 2 të këtij ekuacioni, d.m.th. .

Vështirësia kryesore qëndron pikërisht në gjetjen e zgjidhjeve të pjesshme lineare të pavarura për një ekuacion diferencial të këtij lloji. Në mënyrë tipike, zgjidhjet e veçanta zgjidhen nga sistemet e mëposhtme të funksioneve linearisht të pavarura:


Megjithatë, zgjidhjet e veçanta nuk paraqiten gjithmonë në këtë formë.

Një shembull i një LOD është .

Zgjidhja e përgjithshme e LDDE kërkohet në formën , ku është zgjidhja e përgjithshme e LDDE-së përkatëse dhe është zgjidhja e veçantë e ekuacionit diferencial origjinal. Ne sapo folëm për gjetjen e tij, por mund të përcaktohet duke përdorur metodën e ndryshimit të konstantave arbitrare.

Mund të jepet një shembull i LNDU .

Ekuacionet diferenciale të rendit më të lartë.

Ekuacionet diferenciale që lejojnë një reduktim sipas rendit.

Rendi i ekuacionit diferencial , i cili nuk përmban funksionin e dëshiruar dhe derivatet e tij deri në rendin k-1, mund të reduktohet në n-k duke zëvendësuar .

Në këtë rast, ekuacioni diferencial origjinal do të reduktohet në . Pas gjetjes së zgjidhjes së tij p(x), mbetet të kthehemi në zëvendësim dhe të përcaktojmë funksionin e panjohur y.

Për shembull, ekuacioni diferencial pas zëvendësimit, ai do të bëhet një ekuacion me ndryshore të ndashme dhe rendi i tij do të reduktohet nga i treti në i pari.