Açıların toplamı nedir? Bir üçgenin açılarının toplamı ile ilgili teorem. Açı boyutuna göre türler

Üçgen açıların toplamı- önemli ama yeterli basit tema 7.sınıf geometri dersinde okutulmaktadır. Konu bir teorem, kısa bir kanıt ve çeşitli mantıksal sonuçlardan oluşmaktadır. Bu konuyu bilmek çözüme yardımcı olur geometrik problemler konunun daha sonraki çalışması sırasında.

Teorem - keyfi bir üçgenin açılarının toplamı nedir?

Teorem, türü ne olursa olsun herhangi bir üçgen alırsanız tüm açıların toplamının her zaman 180 derece olacağını belirtir. Bu şu şekilde kanıtlanmıştır:

• örneğin, ABC üçgenini alın, tepe noktasında bulunan B noktasından geçen düz bir çizgi çizin ve bunu "a" olarak belirtin, "a" düz çizgisi AC kenarına kesinlikle paraleldir;
• “a” düz çizgisi ile AB ve BC kenarları arasında, açılar 1 ve 2 sayılarıyla işaretlenerek belirtilir;
• 1 açısı A açısına eşit kabul edilir ve bu açıların çapraz olduğu kabul edildiğinden açı 2, C açısına eşit kabul edilir;
• Böylece, 1, 2 ve 3 açıları (B açısı yerine belirtilen) arasındaki toplam, B tepe noktasıyla açılmış açıya eşit olarak kabul edilir - ve 180 derecedir.

Sayılarla gösterilen açıların toplamı 180 derece ise A, B ve C açılarının toplamı 180 dereceye eşit kabul edilir. Bu kural her üçgen için geçerlidir.

Geometrik teoremden çıkan sonuç

Yukarıdaki teoremin birkaç sonucunu vurgulamak gelenekseldir.

• Sorun dik açılı bir üçgeni ele alıyorsa, açılarından biri varsayılan olarak 90 dereceye eşit olacak ve dar açıların toplamı da 90 derece olacaktır.
• Dik bir ikizkenar üçgenden bahsediyorsak, toplamı 90 dereceye eşit olan dar açıları ayrı ayrı 45 dereceye eşit olacaktır.
• Eşkenar üçgen sırasıyla üç eşit açıdan oluşur, her biri 60 dereceye eşit olacak ve toplamda 180 derece olacaktır.
• Herhangi bir üçgenin dış açısı, kendisine komşu olmayan iki iç açının toplamına eşit olacaktır.

Şu kural çıkarılabilir: Herhangi bir üçgenin en az iki dar açısı vardır. Bazı durumlarda, bir üçgen üç dar açıdan oluşur ve yalnızca iki tane varsa üçüncü açı geniş veya dik olur.

Teorem. Bir üçgenin iç açılarının toplamı iki dik açıya eşittir.

Bir ABC üçgenini alalım (Şekil 208). İç açılarını 1, 2 ve 3 sayılarıyla gösterelim.

∠1 + ∠2 + ∠3 = 180°.

Üçgenin bir köşesinden, örneğin B'den, AC'ye paralel bir MN düz çizgisi çizelim.

B köşesinde üç açımız var: ∠4, ∠2 ve ∠5. Toplamları düz bir açıdır, dolayısıyla 180°'ye eşittir:

∠4 + ∠2 + ∠5 = 180°.

Ancak ∠4 = ∠1 paralel MN ve AC çizgileri ve AB sekantıyla iç çapraz açılardır.

∠5 = ∠3 - bunlar MN ve AC paralel çizgileri ve BC sekantıyla iç çapraz açılardır.

Bu, ∠4 ve ∠5'in, eşitleri olan ∠1 ve ∠3 ile değiştirilebileceği anlamına gelir.

Bu nedenle, ∠1 + ∠2 + ∠3 = 180°. Teorem kanıtlandı.

2. Üçgenin dış açısının özelliği.

Aslında ABC üçgeninde (Şekil 209) ∠1 + ∠2 = 180° - ∠3, fakat aynı zamanda ∠ВСD, bu üçgenin ∠1 ve ∠2'ye komşu olmayan dış açısı da 180°'ye eşittir - ∠3 .

Böylece:

∠1 + ∠2 = 180° - ∠3;

∠BCD = 180° - ∠3.

Bu nedenle, ∠1 + ∠2= ∠BCD.

Bir üçgenin dış açısının türetilmiş özelliği, bir üçgenin dış açısına ilişkin daha önce kanıtlanmış teoremin içeriğini açıklığa kavuşturur; bu teorem, yalnızca bir üçgenin dış açısının, kendisine bitişik olmayan bir üçgenin her bir iç açısından daha büyük olduğunu belirtir; artık dış açının kendisine komşu olmayan her iki iç açının toplamına eşit olduğu tespit edilmiştir.

3. Açısı 30° olan dik üçgenin özelliği.

ACB dik üçgenindeki B açısının 30° olmasına izin verin (Şekil 210). O zaman diğer dar açısı 60° olacaktır.

AC kenarının AB hipotenüsünün yarısına eşit olduğunu kanıtlayalım. AC ayağını C dik açısının tepe noktasının ötesine uzatalım ve AC doğru parçasına eşit bir CM doğru parçasını bir kenara bırakalım. M noktasını B noktasına bağlayalım. Ortaya çıkan ВСМ üçgeni ACB üçgenine eşittir. ABM üçgeninin her bir açısının 60°ye eşit olduğunu, dolayısıyla bu üçgenin eşkenar üçgen olduğunu görüyoruz.

AC kenarı AM'nin yarısına eşittir ve AM, AB'ye eşit olduğundan, AC kenarı AB hipotenüsünün yarısına eşit olacaktır.

Üçgenin iç açılarının toplamı 180 0'dır. Bu Öklid geometrisinin temel aksiyomlarından biridir. Bu, okul çocuklarının çalıştığı geometridir. Geometri, gerçek dünyanın mekansal formlarını inceleyen bilim olarak tanımlanır.

Antik Yunanlıları geometriyi geliştirmeye iten şey neydi? Tarlaları, çayırları - dünya yüzeyinin alanlarını ölçme ihtiyacı. Aynı zamanda eski Yunanlılar da Dünya yüzeyinin yatay ve düz olduğunu kabul ediyorlardı. Bu varsayım dikkate alınarak, 180 0 üçgenin iç açılarının toplamını içeren Öklid aksiyomları oluşturuldu.

Aksiyom, kanıt gerektirmeyen bir önermedir. Bu nasıl anlaşılmalıdır? Kişiye yakışan bir dilek dile getirilir ve ardından illüstrasyonlarla onaylanır. Ancak kanıtlanmayan her şey kurgudur, gerçekte var olmayan bir şeydir.

Alma yeryüzü Yatay olarak, eski Yunanlılar Dünya'nın şeklini otomatik olarak düz olarak kabul ettiler, ancak bu farklı - küresel. Doğada hiçbir yatay düzlem veya düz çizgi yoktur çünkü yerçekimi uzayı büker. Düz çizgiler ve yatay düzlemler yalnızca insan beyninde bulunur.

Dolayısıyla kurgusal dünyanın mekânsal biçimlerini açıklayan Öklid geometrisi bir simulakrdır, aslı olmayan bir kopyadır.

Öklid'in aksiyomlarından biri, bir üçgenin iç açılarının toplamının 180 0 olduğunu belirtir. Aslında, gerçek kavisli uzayda veya Dünya'nın küresel yüzeyinde bir üçgenin iç açılarının toplamı her zaman 180°'den büyüktür.

Şöyle düşünelim. Dünyadaki herhangi bir meridyen ekvatorla 90 0 açıyla kesişir. Bir üçgen elde etmek için başka bir meridyeni meridyenden uzaklaştırmanız gerekir. Meridyenler ile ekvator kenarı arasındaki üçgenin açılarının toplamı 180 0 olacaktır. Ancak direkte hala bir açı olacak. Sonuç olarak tüm açıların toplamı 180 0'dan büyük olacaktır.

Kutupta kenarlar 90 0 açıyla kesişirse, böyle bir üçgenin iç açılarının toplamı 270 0 olacaktır. Bu üçgende ekvatoru dik açıyla kesen iki meridyen birbirine paralel olacak, kutupta birbirini 90 0 açıyla kesen iki meridyen dik olacaktır. Aynı düzlemdeki iki paralel çizginin sadece kesişmekle kalmayıp aynı zamanda kutupta dik olabileceği ortaya çıktı.

Tabii ki, böyle bir üçgenin kenarları düz çizgiler olmayacak, küresel şekli tekrarlayan dışbükey olacaktır. küre. Ancak bu tam olarak uzayın gerçek dünyasıdır.

19. yüzyılın ortalarındaki eğriliği dikkate alarak gerçek uzayın geometrisi. Alman matematikçi B. Riemann (1820-1866) tarafından geliştirilmiştir. Ancak okul çocuklarına bundan bahsedilmiyor.

Yani, Dünya'nın yatay yüzeyli düz şeklini alan, aslında öyle olmayan Öklid geometrisi bir simulakrdır. Nootik, uzayın eğriliğini hesaba katan Riemann geometrisidir. İçindeki üçgenin iç açılarının toplamı 180 0'dan büyüktür.

Kanıt

İzin vermek ABC" - keyfi üçgen. Hadi zirveye doğru ilerleyelim B çizgiye paralel çizgi AC. (böyle bir düz çizgiye Öklid düz çizgisi denir). Üzerine bir nokta koyalım D böylece noktalar A Ve D düz bir çizginin karşıt taraflarında uzanmak M.Ö..Açılar DBC Ve ACB bir sekant tarafından oluşturulan iç çapraz uzanmaya eşit M.Ö. paralel çizgilerle AC. Ve BD. Bu nedenle bir üçgenin köşe noktalarındaki açılarının toplamı B Ve İLE açıya eşit ABD.Bir üçgenin üç açısının toplamı, iç açılarının toplamına eşittir. ABD Ve BAC. Bu açılar paralel iç açılar olduğundan tek taraflıdır. AC. Ve BD sekant'ta AB, toplamları 180° olur. Teorem kanıtlandı.

Sonuçlar

Teoremden herhangi bir üçgenin iki dar açısı olduğu sonucu çıkar. Aslında, çelişki yoluyla ispatı kullanarak, üçgenin yalnızca bir dar açısı olduğunu veya hiç dar açısı olmadığını varsayalım. O halde bu üçgenin her biri en az 90° olan en az iki açısı vardır. Bu açıların toplamı 180°'den az değildir. Ancak üçgenin tüm açılarının toplamı 180° olduğundan bu imkansızdır. Q.E.D.

Simpleks teorisine genelleme

Simpleks'in i ve j yüzleri arasındaki açı nerede.

Notlar

• Küre üzerinde bir üçgenin açılarının toplamı her zaman 180°'yi aşar, farka küresel fazlalık denir ve üçgenin alanıyla orantılıdır.
• Lobaçevski düzleminde bir üçgenin açılarının toplamı her zaman 180°'den küçüktür. Fark aynı zamanda üçgenin alanıyla da orantılıdır.

Ayrıca bakınız

Wikimedia Vakfı. 2010.

Diğer sözlüklerde “Bir üçgenin açılarının toplamına ilişkin teoremin” ne olduğuna bakın:

Öklid geometrisinde çokgenlerin özelliği: Bir üçgenin n açılarının toplamı 180°(n 2)'dir. İçindekiler 1 Kanıt 2 Not ... Vikipedi

Pisagor teoremi, bir dik üçgenin kenarları arasındaki ilişkiyi kuran Öklid geometrisinin temel teoremlerinden biridir. İçindekiler 1 ... Vikipedi

Pisagor teoremi, bir dik üçgenin kenarları arasındaki ilişkiyi kuran Öklid geometrisinin temel teoremlerinden biridir. İçindekiler 1 İfade 2 Kanıt ... Vikipedi

Kosinüs teoremi, Pisagor teoreminin bir genellemesidir. Bir üçgenin bir kenarının karesi, diğer iki kenarın karelerinin toplamına, bu kenarların çarpımının iki katı ile aralarındaki açının kosinüsü olmadan eşittir. Bir düzlem üçgen için a,b,c kenarları ve α açısı... ... Vikipedi

Bu terimin başka anlamları da vardır, bkz. Üçgen (anlamlar). Bir üçgen (Öklid uzayında) geometrik şekil aynı düz çizgi üzerinde yer almayan üç noktayı birleştiren üç parçadan oluşur. Üç nokta,... ... Vikipedi

Standart gösterim Bir üçgen, 3 köşesi (açı) ve 3 kenarı olan en basit çokgendir; Aynı doğru üzerinde yer almayan üç nokta ve bu noktaları çiftler halinde birbirine bağlayan üç parça ile sınırlanan düzlemin parçası. Bir üçgenin köşeleri ... Vikipedi

Antik Yunan matematikçisi. 3. yüzyılda İskenderiye'de çalıştı. M.Ö e. Ana çalışma Antik matematiğin, temel geometrinin, sayılar teorisinin temellerini içeren “İlkeler” (15 kitap), genel teori Alan ve hacimlerin belirlenmesine yönelik ilişkiler ve yöntemler,... ... ansiklopedik sözlük

- (MÖ 275 ile 270 arasında öldü) eski Yunan matematikçisi. Doğum zamanı ve yeri hakkında bilgi bize ulaşmadı, ancak Öklid'in İskenderiye'de yaşadığı ve faaliyetinin en parlak döneminin Mısır'daki I. Ptolemy döneminde gerçekleştiği biliniyor... ... Büyük Ansiklopedik Sözlük

Geometri, şekillerin hareketini tanımlaması açısından Öklid geometrisine benzer, ancak beş önermesinden birinin (ikinci veya beşinci) olumsuzlanmasıyla değiştirilmesi açısından Öklid geometrisinden farklıdır. Öklid önermelerinden birinin olumsuzlanması... ... Collier Ansiklopedisi

Üçgen . Dar, geniş ve dik üçgen.

Bacaklar ve hipotenüs. İkizkenar ve eşkenar üçgen.

Bir üçgenin açılarının toplamı.

Bir üçgenin dış açısı. Üçgenlerin eşitliğinin işaretleri.

Bir üçgende dikkate değer çizgiler ve noktalar: yükseklikler, kenarortaylar,

ortancalar, medyan e dikler, diklik merkezi,

ağırlık merkezi, çevrelenmiş bir dairenin merkezi, yazılı bir dairenin merkezi.

Pisagor teoremi. Rastgele bir üçgende en boy oranı.

Üçgen üç tarafı (veya üç açısı) olan bir çokgendir. Bir üçgenin kenarları genellikle aşağıdakilere karşılık gelen küçük harflerle gösterilir: büyük harfler, zıt köşeleri gösterir.

Her üç açı da dar ise (Şekil 20), o zaman bu dar üçgen . Açılardan biri doğruysa(C, Şekil 21), yani dik üçgen; taraflara, bdik açı oluşturanlara denir bacaklar; tarafCdik açının karşısına denir hipotenüs. Eğer biri geniş açılar (B, Şekil 22), yani geniş açılı üçgen.


ABC Üçgeni (Şekil 23) - ikizkenar, Eğer iki kenarları eşittir (A= C); bu eşit kenarlara denir yanal, üçüncü taraf çağrılır temelüçgen. Üçgen ABC (Şek. 24) – eşkenar, Eğer Tüm kenarları eşittir (A = B = C). Genel olarak ( A ≠ B ≠ C) sahibiz skalenüçgen .

Üçgenlerin temel özellikleri. Herhangi bir üçgende:

1. Büyük tarafın karşısında daha büyük açı bulunur ve bunun tersi de geçerlidir.

2. Eşit açılar eşit kenarların karşısında yer alır ve bunun tersi de geçerlidir.

Özellikle tüm açılar eşkenarüçgen eşittir.

3. Üçgenin iç açılarının toplamı 180'dir º .

Son iki özellikten eşkenardaki her açının olduğu sonucu çıkar.

üçgen 60'tır º.

4. Üçgenin kenarlarından birinden devam edilirse (AC, Şek. 25), alıyoruz harici

BCD açısı . Üçgenin dış açısı iç açılarının toplamına eşittir,

ona bitişik değil : BCD = A + B.

5. Herhangi Üçgende bir kenar diğer iki kenarın toplamından küçük ve büyüktür

onların farklılıkları (A < B + C, A > B – C;B < A + C, B > A – C;C < A + B,C > A – B).

Üçgenlerin eşitliğinin işaretleri.

Üçgenler sırasıyla eşitse eştir:

A ) iki kenar ve aralarındaki açı;

B ) iki köşe ve onlara bitişik olan taraf;

c) üç taraf.

Dik üçgenlerin eşitlik işaretleri.

İki dikdörtgen Aşağıdaki koşullardan biri doğruysa üçgenler eşittir:

1) bacakları eşittir;

2) bir üçgenin kenarı ve hipotenüsü diğerinin kenarı ve hipotenüsüne eşittir;

3) bir üçgenin hipotenüsü ve dar açısı diğerinin hipotenüsüne ve dar açısına eşittir;

4) bir üçgenin bacağı ve bitişik dar açısı diğerinin bacağına ve bitişik dar açısına eşittir;

5) bacak ve bir üçgenin karşı dar açısı bacağa eşittir ve diğerinin zıt dar açısı.

Üçgendeki harika çizgiler ve noktalar.

Yükseklik üçgendik,herhangi bir tepe noktasından karşı tarafa indirildi ( veya devamı). Bu tarafa denirüçgenin tabanı . Bir üçgenin üç yüksekliği her zaman kesişirbir noktada, isminde diklik merkeziüçgen. Dar bir üçgenin ortomerkezi (noktaÖ , Şekil 26) üçgenin içinde bulunur vegeniş bir üçgenin diklik merkezi (noktaÖ , şekil 27) – dıştan; Bir dik üçgenin diklik merkezi, dik açının tepe noktasıyla çakışır.

Medyan - Bu çizgi segmenti Bir üçgenin herhangi bir köşesini karşı kenarın ortasına bağlamak. Bir üçgenin üç medyanı (AD, BE, CF, şek.28) bir noktada kesişmek Ö , daima üçgenin içinde yer alır ve onun olmak ağırlık merkezi. Bu nokta, her medyanı tepe noktasından itibaren sayarak 2:1 oranında böler.

Açıortay - Bu açıortay segmenti tepe noktasından noktaya açı karşı tarafla kesişmeler. Bir üçgenin üç açıortayı (AD, BE, CF, şek. 29) bir noktada kesişmek Ah, her zaman üçgenin içinde yatıyorum Ve yapı yazılı dairenin merkezi(bkz. “Yazılıve çevrelenmiş çokgenler").

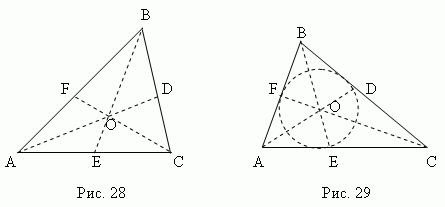
Açıortay, karşı tarafı bitişik kenarlarla orantılı parçalara böler ; örneğin, Şekil 29'da AE: CE = AB: BC.

Ortanca dik ortasından çizilen bir dikmedir segment noktaları (yanlar). ABC üçgeninin üç dik açıortayı(KO, MO, HAYIR, Şekil 30 ) bir O noktasında kesişir, bu da merkez sınırlı daire (K, M, N noktaları – Üçgenin kenarlarının orta noktaları ABC).

Dar bir üçgende bu nokta üçgenin içinde yer alır; geniş - dışarıda; dikdörtgen şeklinde - hipotenüsün ortasında. Ortocenter, ağırlık merkezi, çevre merkezi ve yazılı daire yalnızca eşkenar üçgende çakışır.

Pisagor teoremi. Bir dik üçgende uzunluğun karesiHipotenüs, bacakların uzunluklarının karelerinin toplamına eşittir.

Pisagor teoreminin kanıtı Şekil 31'den açıkça görülmektedir. Bir dik üçgen düşünün Bacakları olan ABC a, b ve hipotenüs C.

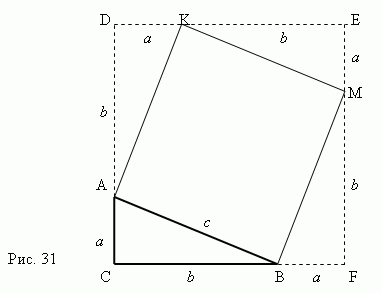
Bir kare inşa edelim AKMB hipotenüsü kullanma AB bir taraf olarak. Daha sonrasağ üçgenin kenarlarına devam edin ABC bir kare elde etmek için CDEF kenarları eşit olana + b .Şimdi karenin alanının açık olduğu açıktır. CDEF eşittir ( a+b) 2 . Öte yandan bu alan toplamına eşittir alanlar dört dik üçgen ve AKMB meydanı, yani

C 2 + 4 (ab / 2) = C 2 + 2 ab,

buradan,

C 2 + 2 ab= (a+b) 2 ,

ve sonunda elimizde:

C 2 =A 2 + b 2 .

Rastgele bir üçgende en boy oranı.

Genel durumda (keyfi bir üçgen için) elimizde:

C 2 =A 2 + b 2 – 2ab· çünkü C,

nerede C – kenarlar arasındaki açıA Ve B .