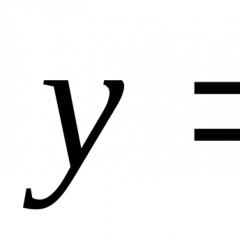Noto'g'ri integrallarni yig'ish uchun testlar. Noto'g'ri integralni qanday hisoblash va uning yaqinlashuvini aniqlash. Ta'rif va asosiy xususiyatlar

12.11 teorema (noto'g'ri integrallarni solishtirish uchun test). f(x) va g(x) funksiyalar [a, ">) oraliqda uzluksiz bo'lsin va undagi 0 tuzatish) ?(x) sharti qanoatlansin. Keyin integralning yaqinlashuvidan

integral yaqinlashadi

va aksincha, (12.64) integralning divergentsiyasidan (12.63) integralning ajralishi kelib chiqadi.

Isbot. Keling, quyidagi belgini kiritamiz:

Funktsiya P(K) kamaymaydi; aslida, agar va men 2, keyin

J tuzatish) dx>0 va keyin

Keling, qiymatlar ketma-ketligini olaylik (/?„) -> “>; keyin funksiya qiymatlarining mos keladigan ketma-ketligi (F(Rn)) monoton va kamaymaydi. (12.63) integral yaqinlashsin, keyin ketma-ketlik (67 () R u)) cheklangan; lekin keyin ketma-ketlik ham cheklangan (F(/?„)), demak, 7.13 teorema bo‘yicha u yaqinlashadi. Shuning uchun chegara bor F(R) da R-+ «>, ya'ni. integral (12.64) yaqinlashadi.

Endi teoremaning ikkinchi qismini isbotlaymiz; (12.64) integrali ajralsin. Agar (12.63) integral yaqinlashadi deb faraz qilsak, yuqorida isbotlanganidek, (12.64) integral ham yaqinlashishi kerak, bu esa shartga ziddir. Teorema isbotlangan. ?

Izoh. Xuddi shunday taqqoslash mezoni ikkinchi turdagi noto'g'ri integrallar uchun ham amal qiladi. Agar /(x) funktsiyalari va g (X) yarim oraliqda uzluksiz [a>b) va birlik nuqtaning ba'zi qo'shnilaridagi barcha nuqtalar uchun b yakunlandi

shartlar 0 (x), u holda Jg(x)dx integralining yaqinlashuvidan shunday kelib chiqadi

J/(x)dx integralning divergensiyasi, J/(x)dx integralining divergensiyasi -

Jg(x)dx integralning kuchi.

Noto'g'ri integrallarning yaqinlashuvini o'rganish uchun misollarni ko'rib chiqaylik.

27-misol. T. ^-.

X 3 (1 + e L)

Yechim. Ushbu integraldagi integralni funksiya bilan solishtiraylik

Dg. Ko'rinib turibdiki -r-

X g* (1+0 x J

gral J-jdx yaqinlashadi; shuning uchun taqqoslash mezoni tufayli berilgan 1 X

nal integral.

28-misol. I-.

Yechim. Ushbu integralning integralini 1/x funksiyasi bilan solishtirib,

1 oraliqda (1 + In x)/x > 1/x ekanligini ko‘ramiz

diversifikatsiya qiladi, shuning uchun taqqoslaganda, bu integral ham ajralib chiqadi.

Xulosa qilib aytganda, birinchi turdagi noto'g'ri integralning yaqinlashuvi uchun Koshi mezonini isbotsiz keltiramiz.

12.10.4. Noto'g'ri integrallarning mutlaq va shartli yaqinlashuvi

Ta'rif 5. J/(x)dx noto'g'ri integral deyiladi mutlaqo

konvergent, J|/(x)|dx integrali yaqinlashsa.

Ta'rif 6. J /(x) dx noto'g'ri integrali deyiladi shartli ravishda o'xshash

davomli, agar u yaqinlashsa va J|/(x)|dx integrali ajralib chiqsa.

E'tibor bering, integralning mutlaq yaqinlashuvi uning 3 bahosi tufayli yaqinlashishini anglatadi aniq integral va Koshi mezoni.

12.13 teorema (Dirichlet-Abel testi*). /(x) funksiya uzluksiz va chegaralangan anti hosilaga ega bo'lsin F(x) [a, «>] oraliqda va g(x) funksiya bu oraliqda uzluksiz hosilaga ega, x -> ©o bo‘lgani uchun ortib ketmaydi va nolga intiladi. Keyin noto'g'ri integral

birlashadi.

Isbot. J /(x)g(x)dx integraliga qismlar bo'yicha integrallashni qo'llaymiz

ixtiyoriy segmentda R R"[ bilan A, °°). Bizda ... bor:

12.12 teorema. Noto'g'ri integral (12.64) yaqinlashish uchun har qanday e > 0 uchun bunday sonni topish zarur va etarli. A> 0, bu har qanday uchun R" va /?", dan katta A, tengsizlik amal qiladi:

Teorema shartlariga ko'ra F(x) cheklangan, ya'ni. |F(x)| K. g(x) funksiya ortib ketmaydi va x -” “> sifatida nolga intiladi, ya’ni. g(x)> 0, a g"(x)

Abel Niels Henrik (1802-1829) - norvegiyalik matematik.

Teorema shartlariga ko'ra, x -> ©° uchun g(x) -» 0 bo'lgani uchun, ixtiyoriy e > 0 soni uchun sonni topishimiz mumkin. A> shunday qachon R" > L tengsizlik qanoatlantiriladi g(R") Buni (12.68) bahoga almashtirib, biz quyidagilarni olamiz:

bu integralning yaqinlashuvining Koshi mezoniga mos keladi (12.66). Teorema isbotlangan. ?

Noto'g'ri integrallarni yig'ish uchun Dirixlet-Abel testidan foydalanish misollarini ko'rib chiqaylik.

29-misol. f^^dx, a>0.

Yechim. Keling, /(x) = sin x, g(x)= l/x"; teoremaning barcha shartlari bajarilganligini tekshirish oson, ya'ni bu integral yaqinlashadi. a > 1 uchun bu integral

ral mutlaqo birlashadi. Darhaqiqat, |gunoh x/xP 1/d L, integral J(l/x e)dx

birlashadi, ya'ni. Taqqoslash mezoni (12.11 teorema) bo'yicha bu integral ham mutlaq yaqinlashadi.

30-misol. Jsin x 2 dx - Fresnel integrali, o

Yechim. Keling, bu integralni yig'indi sifatida ifodalaymiz:

Chunki gunoh x 2 - doimiy funktsiya oralig'ida (0, 1J, (12.69) da birinchi integral mavjud. (12.69) ning o'ng tomonidagi noto'g'ri integralning yaqinlashishini aniqlash uchun biz /(x) = x sin x 2 ni o'rnatamiz, g(x) = 1/x. Keyin /(x) funksiyasi uchun antiderivativ F(x) = -cosx 2 /!|1, ">) oraliqda chegaralangan va #(x) musbat, x -" °° sifatida nolga intiladi va (1, ©o) da uzluksiz hosilaga ega. Bu Dirixlet-Abel mezoniga ko'ra, (12.69) dagi ikkinchi integral yaqinlashadi, ya'ni. Fresnel integrali ham yaqinlashadi.

Ma'lumki, integralni topish juda qiyin vazifa bo'lishi mumkin. Noto'g'ri integralni hisoblashni boshlash va uni yo'lning oxirida topish katta umidsizlik bo'lar edi. Shuning uchun, bir turdagi funktsiyalarga asoslangan jiddiy hisob-kitoblarsiz, noto'g'ri integralning yaqinlashishi yoki divergentsiyasi haqida xulosa chiqarishga imkon beradigan usullar qiziqish uyg'otadi. Quyida ko'rib chiqiladigan birinchi va ikkinchi taqqoslash teoremalari konvergentsiya uchun noto'g'ri integrallarni o'rganishga katta yordam beradi.

f(x)?0 bo'lsin. Keyin funktsiyalar

t yoki -g o'zgaruvchilarda monoton ravishda ortib bormoqda (chunki biz g>0 qabul qilamiz, -g chapdan nolga intiladi). Agar argumentlar ortib borishi bilan F 1 (t) va F 2 (-d) funksiyalar yuqoridan chegaralangan bo‘lib qolsa, bu mos keladigan noto‘g‘ri integrallarning yaqinlashishini bildiradi. Bu manfiy bo'lmagan funksiyalar integrallari uchun birinchi taqqoslash teoremasining asosidir.

x?a dagi f(x) va g(x) funksiyalar quyidagi shartlarni qanoatlantirsin:

• 1) 0?f(x)?g(x);
• 2) f(x) va g(x) funksiyalar uzluksizdir.

U holda integralning yaqinlashuvidan integralning yaqinlashuvi, integralning ajralishidan esa divergensiya kelib chiqadi.

0?f(x)?g(x) va funksiyalar uzluksiz ekan, demak

Shartga ko'ra, integral yaqinlashadi, ya'ni. cheklangan qiymatga ega. Shuning uchun integral ham yaqinlashadi.

Endi integral ajralsin. Faraz qilaylik, integral yaqinlashadi, lekin keyin integral yaqinlashishi kerak, bu esa shartga zid keladi. Bizning taxminimiz noto'g'ri, integral ajralib chiqadi.

2-turdagi noto'g'ri integrallar uchun taqqoslash teoremasi.

oraliqda f(x) va g(x) funksiyalar uchun x>+0 uchun cheksiz orttiring. x>+0 uchun quyidagi tengsizlik bajariladi:<. Несобственный интеграл есть эталонный интеграл 2-го рода, который при p=<1 сходится; следовательно, по 1-й теореме сравнения для несобственных интегралов 2-го рода интеграл сходится также.

1-turdagi noto'g'ri integrallar uchun taqqoslash teoremasi.

f(x) va g(x) funksiyalari intervalda bo'lsin va integrallash segmenti chekli, ya'ni cheksizlik bilan emas, balki sonlar bilan cheklangan. Ba'zi vazifalar ushbu cheklovlardan voz kechish zarurligiga olib keladi. Noto'g'ri integrallar shunday paydo bo'ladi.

Noto'g'ri integralning geometrik ma'nosi Bu juda oddiy bo'lib chiqadi. Funktsiyaning grafigi bo'lgan holatda y = f(x) eksa ustida joylashgan ho'kiz, aniq integral egri chiziq bilan chegaralangan egri chiziqli trapetsiya maydonini ifodalaydi. y = f(x) , x o'qi va ordinatalar x = a , x = b. O'z navbatida, noto'g'ri integral chiziqlar orasiga o'ralgan cheksiz (cheksiz) egri chiziqli trapezoidning maydonini ifodalaydi. y = f(x) (quyidagi rasmda - qizil), x = a va abscissa o'qi.

Noto'g'ri integrallar boshqa cheksiz intervallar uchun ham xuddi shunday aniqlanadi:

Cheksiz kavisli trapetsiyaning maydoni chekli son bo'lishi mumkin, bu holda noto'g'ri integral konvergent deb ataladi. Maydon ham cheksiz bo'lishi mumkin va bu holda noto'g'ri integral divergent deb ataladi.

Noto'g'ri integral o'rniga integral chegarasidan foydalanish. Noto'g'ri integralni baholash uchun aniq integralning chegarasidan foydalanish kerak. Agar bu chegara mavjud bo'lsa va chekli bo'lsa (cheksizlikka teng bo'lmasa), unda noto'g'ri integral konvergent deb ataladi, aks holda - divergent. O'zgaruvchining chegara belgisi ostida nimaga moyilligi biz birinchi turdagi noto'g'ri integral yoki ikkinchi turdagi integral bilan ishlayotganimizga bog'liq. Keling, bu haqda hozir bilib olaylik.

Birinchi turdagi noto'g'ri integrallar - cheksiz chegaralar va ularning yaqinlashuvi

Cheksiz yuqori chegarali noto'g'ri integrallar

Demak, noto‘g‘ri integral yozish odatdagi aniq integraldan integrasiyaning yuqori chegarasi cheksiz ekanligi bilan farq qiladi.

Ta'rif. Uzluksiz funktsiyani integrallashning cheksiz yuqori chegarasi bilan noto'g'ri integral f(x) dan oraliqda a oldin ∞ bu funksiyaning integralining integrallashning yuqori chegarasi bilan chegarasi deyiladi b va integratsiyaning pastki chegarasi a integratsiyaning yuqori chegarasi cheksiz o'sishi sharti bilan, ya'ni.

.

Agar bu chegara mavjud bo'lsa va cheksizlikdan ko'ra qandaydir songa teng bo'lsa, u holda noto'g'ri integral konvergent deyiladi, va chegara teng bo'lgan son uning qiymati sifatida qabul qilinadi. Aks holda noto'g'ri integral divergent deyiladi va unga hech qanday ma'no berilmaydi.

1-misol. Noto'g'ri integralni hisoblang(agar u birlashsa).

Yechim. Noto'g'ri integralning ta'rifiga asoslanib, biz topamiz

Chegara mavjud va 1 ga teng bo'lgani uchun, bu noto'g'ri integral yaqinlashadi va 1 ga teng.

Quyidagi misolda integral 1-misoldagi kabi deyarli bir xil, faqat x darajasi ikkita emas, balki alfa harfi bo'lib, konvergentsiya uchun noto'g'ri integralni o'rganish vazifasi qo'yilgan. Ya'ni, savolga javob berish kerak: bu noto'g'ri integral alfa ning qaysi qiymatlarida yaqinlashadi va qaysi qiymatlarda ajralib chiqadi?

2-misol. Noto'g'ri integralni yaqinlashish uchun tekshiring(integratsiyaning pastki chegarasi noldan katta).

Yechim. Keling, avval shunday deb taxmin qilaylik, keyin

Olingan ifodada biz chegaraga o'tamiz:

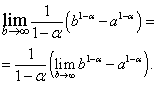
O'ng tarafdagi chegara mavjudligini va qachon nolga teng ekanligini ko'rish oson, ya'ni qachon mavjud emas, ya'ni.

Birinchi holda, ya'ni qachon . Agar , keyin va mavjud emas.

Tadqiqotimizning xulosasi quyidagicha: bu noto'g'ri integral yaqinlashadi da va farqlanadi da .

O'rganilayotgan noto'g'ri integral turiga Nyuton-Leybnits formulasini qo'llash , siz unga juda o'xshash quyidagi formulani olishingiz mumkin:

.

Bu umumlashtirilgan Nyuton-Leybnits formulasi.

3-misol. Noto'g'ri integralni hisoblang(agar u birlashsa).

Ushbu integralning chegarasi mavjud:

Asl integralni ifodalovchi yig'indini tashkil etuvchi ikkinchi integral:

Ushbu integralning chegarasi ham mavjud:

.

Biz ikkita integralning yig'indisini topamiz, bu ham ikkita cheksiz chegarali dastlabki noto'g'ri integralning qiymati:

Ikkinchi turdagi noto'g'ri integrallar - cheksiz funktsiyalardan va ularning yaqinlashuvidan

Funktsiyaga ruxsat bering f(x) dan segmentida berilgan a oldin b va unda cheksizdir. Faraz qilaylik, funksiya nuqtada cheksizlikka boradi b , segmentning boshqa barcha nuqtalarida esa uzluksiz.

Ta'rif. Funktsiyaning noto'g'ri integrali f(x) dan segmentida a oldin b bu funksiyaning integralining integrallashning yuqori chegarasi bilan chegarasi deyiladi c , agar intilish paytida c Kimga b funksiya chegarasiz va nuqtada ortadi x = b funksiya aniqlanmagan, ya'ni.

.

Agar bu chegara mavjud bo'lsa, ikkinchi turdagi noto'g'ri integral konvergent deb ataladi, aks holda u divergent deb ataladi.

Nyuton-Leybnits formulasidan foydalanib, biz hosil qilamiz.

1. Cheksiz chegarali noto'g'ri integrallar

Keling, integralning integral yig'indisining chegarasi sifatidagi ta'rifini eslaylik:

Ta'rifda integrallash oralig'i chekli, f(x) funksiya esa uning ichida uzluksiz bo'ladi. Ushbu taxminlarning buzilishi noto'g'ri integrallarga olib keladi.

Ta'rif. Agar integral cheksiz ortib borishi bilan chekli chegaraga moyil bo'lsa "b", u holda bu chegara f (x) funktsiyaning cheksiz yuqori chegarasi bilan noto'g'ri integral deb ataladi va belgisi bilan belgilanadi.

Bunday holda, noto'g'ri integral mavjud yoki yaqinlashadi deyiladi.

Agar belgilangan chegara mavjud bo'lmasa yoki mavjud bo'lsa, lekin cheksiz bo'lsa, u holda integral mavjud emas yoki ajralib chiqadi deb aytiladi.

Cheksiz pastki chegaraga ega noto'g'ri integral xuddi shunday aniqlanadi:

Ikki cheksiz chegaraga ega noto'g'ri integral quyidagicha ifodalanadi:

Bu erda c - Ox o'qidagi har qanday sobit nuqta.

Demak, noto'g'ri integrallar cheksiz pastki chegaraga, cheksiz yuqori chegaraga va ikkita cheksiz chegaraga ega bo'lishi mumkin.

Konvergentsiya belgilari. Mutlaq va shartli yaqinlashuv

Integralning har biri mavjud bo'lgandagina integral mavjud bo'ladi: va .

Misol. Integralning yaqinlashuvini tekshiring

c = 0 deb faraz qilsak, biz quyidagilarni olamiz:

bular. integral yaqinlashadi.

Ba'zan noto'g'ri integralni hisoblashning hojati yo'q, lekin uni boshqa integral bilan solishtirish orqali uning yaqinlashishi yoki uzoqlashishini bilish kifoya.

Noto'g'ri integrallar uchun taqqoslash teoremasi.

Intervaldagi f (x) funktsiyasi birinchi turdagi bir nechta (cheklangan sonli) uzilish nuqtalariga ega bo'lsin, bu "to'siq" segmentni uzilish nuqtalari bilan bir nechta segmentlarga bo'lish, har bir alohida bo'limda aniq integrallarni hisoblash va natijalarni qo'shish.

Segmentning uchlaridan biriga yaqinlashganda cheksiz bo'lgan funksiyaning aniq integralini ko'rib chiqamiz, masalan, .

(Bunday hollarda ular odatda: ''Funksiya integratsiya oralig'ining o'ng uchida cheksiz uzilishga ega'' deyishadi.)

Bu erda integralning odatiy ta'rifi o'z ma'nosini yo'qotishi aniq.

Ta'rif. £ x uchun uzluksiz f(x) funksiyaning noto'g'ri integrali< b и неограниченной при x ® b - 0, называется предел:

Segmentning chap uchida cheksiz uzilishga ega bo'lgan funksiyaning noto'g'ri integrali ham xuddi shunday aniqlanadi:

Demak, [-1, 0] bo'limida integral ajralib chiqadi.

Demak, integral kesmada ham ajraladi.

Shunday qilib, bu integral butun intervalda [-1, 1] ajraladi. E'tibor bering, agar biz bu integralni x = 0 nuqtadagi integralning uzilishiga e'tibor bermasdan hisoblay boshlasak, noto'g'ri natijaga erishamiz. Haqiqatan ham,

, bu mumkin emas.

Demak, uzluksiz funktsiyaning noto'g'ri integralini o'rganish uchun uni bir necha integrallarga "bo'lish" va ularni o'rganish kerak.

Agar integrallashning (cheklangan) intervalida ikkinchi turdagi uzilish bo'lsa, biz ikkinchi turdagi noto'g'ri integral haqida gapiramiz.

10.2.1 Ta'rif va asosiy xususiyatlar

Integratsiya oralig'ini $\left[ a, \, b \right ]$ bilan belgilaymiz; bu raqamlarning ikkalasi ham quyida chekli deb hisoblanadi. Agar faqat 1 ta uzilish bo'lsa, u $a$ nuqtasida yoki $b$ nuqtasida yoki $(a,\,b)$ oralig'ida joylashgan bo'lishi mumkin. Avval $a$ nuqtada ikkinchi turdagi uzilish mavjud bo'lganda, boshqa nuqtalarda esa integratsiya funksiyasi uzluksiz bo'lgan holatni ko'rib chiqamiz. Shunday qilib, biz integralni muhokama qilamiz

\begin(tenglama) I=\int _a^b f(x)\,dx, (22) \label(intr2) \end(tenglama)

va $f(x) \rightarrow \infty $ qachon $x \rightarrow a+0$. Avvalgidek, birinchi navbatda, bu iboraga ma'no berish kerak. Buning uchun integralni ko'rib chiqing

\[ I(\epsilon)=\int _(a+\epsilon)^b f(x)\,dx. \]

Ta'rif. Cheklangan chegara bo'lsin

\[ A=\lim _(\epsilon \rightarrow +0)I(\epsilon)=\lim _(\epsilon \rightarrow +0)\int _(a+\epsilon)^b f(x)\,dx. \]

Keyin ikkinchi turdagi noto'g'ri integrali (22) yaqinlashadi va unga $A$ qiymati beriladi; $f(x)$ funktsiyasining o'zi $\left[ a, \ intervalida integrallash mumkin deyiladi. , b\right]$.

Integratsiya oralig'ining yuqori chegarasida integral funksiyada ikkinchi turdagi uzilish mavjud bo'lganda variantni ko'rib chiqamiz. Bu holatni $x=-t$ oʻzgaruvchisini oʻzgartirish va keyin integratsiya chegaralarini qayta tartibga solish orqali oldingi holatga keltirish mumkin.

Integratsiya funksiyasi $c \in (a,\,b)$ nuqtada integrallash oralig'ida ikkinchi turdagi uzilishga ega bo'lgan variantni ko'rib chiqamiz. Bunday holda, asl integral

\begin(tenglama) I=\int _a^bf(x)\,dx (23) \label(intr3) \end(tenglama)

summa sifatida taqdim etiladi

\[ I=I_1+I_2, \quad I_1=\int _a^cf(x)\,dx +\int _c^df(x)\,dx. \]

Ta'rif. Agar ikkala $I_1, \, I_2$ integrallari yaqinlashsa, u holda noto'g'ri integral (23) konvergent deb ataladi va $I_1, \, I_2$ integrallari yig'indisiga teng qiymat beriladi, $f(x)$ funksiyasi. $\left [a, \, b\right]$ oralig'ida integrallanuvchi deyiladi. Agar $I_1,\, I_2$ integrallaridan kamida bittasi divergent bo'lsa, noto'g'ri integral (23) divergent deyiladi.

2-turdagi konvergent noto'g'ri integrallar oddiy aniq integrallarning barcha standart xossalariga ega.

1. Agar $f(x)$, $g(x)$ $\left[ a, \,b \right ]$ intervalida integrallash mumkin boʻlsa, ularning yigʻindisi $f(x)+g(x)$ boʻladi. bu oraliqda ham integrallash mumkin va \[ \int _a^(b)\left(f(x)+g(x)\right)dx=\int _a^(b)f(x)dx+\int _a^( b)g (x)dx. \] 2. Agar $f(x)$ $\left[ a, \, b \right ]$ intervalida integrallansa, har qanday $C$ doimiysi uchun $C\cdot f(x)$ funksiyasi ham boʻladi. bu oraliqda integrallanadigan va \[ \int _a^(b)C\cdot f(x)dx=C \cdot \int _a^(b)f(x)dx. \] 3. Agar $f(x)$ $\left[ a, \, b \right ]$ intervalida va bu $f(x)>0$ intervalida integrallansa, \[ \int _a^ (b ) f(x)dx\,>\,0. \] 4. Agar $f(x)$ $\left[ a, \, b \right ]$ intervalida integrallansa, har qanday $c\in (a, \,b)$ uchun integrallar \[ \ int _a^ (c) f(x)dx, \quad \int _c^(b) f(x)dx \] ham yaqinlashadi va \[ \int _a^(b)f(x)dx=\int _a ^(c ) f(x)dx+\int _c^(b) f(x)dx \] (integralning interval boʻyicha qoʻshilishi).

Integralni ko'rib chiqing

\begin(tenglama) I=\int _0^(1)\frac(1)(x^k)\,dx. (24) \label(mod2) \end(tenglama)

Agar $k>0$ bo'lsa, integral $x \rightarrow +0$ sifatida $\infty$ ga intiladi, shuning uchun integral ikkinchi turdagi noto'g'ri. Funktsiya bilan tanishtiramiz

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx. \]

Bu holda antiderivativ ma'lum, shuning uchun

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x^k)\,dx\,=\frac(x^(1-k))(1-k )|_(\epsilon)^1= \frac(1)(1-k)-\frac(\epsilon ^(1-k))(1-k). \]

$k \neq 1$ uchun,

\[ I(\epsilon)=\int _(\epsilon)^(1)\frac(1)(x)\,dx\,=lnx|_(\epsilon)^1= -ln \epsilon. \]

$k = 1$ uchun. $\epsilon \rightarrow +0$ dagi xatti-harakatni hisobga olsak, biz (20) integral $k ga yaqinlashadi degan xulosaga kelamiz.

10.2.2 2-turdagi noto'g'ri integrallarni yig'ish uchun testlar

Teorema (taqqoslashning birinchi belgisi). $f(x)$, $g(x)$ $x\in (a,\,b)$ va $0 uchun uzluksiz bo'lsin 1. Agar integral \[ \int _a^(b)g(x) bo'lsa. dx \] yaqinlashadi, keyin integrali \[ \int _a^(b)f(x)dx yaqinlashadi. \] 2. Agar \[ \int _a^(b)f(x)dx \] integrali ajralib chiqsa, u holda \[ \int _a^(b)g(x)dx integrali ajralib chiqadi. \]

Teorema (ikkinchi taqqoslash mezoni). $f(x)$, $g(x)$ $x\in (a,\,b)$ uchun uzluksiz va musbat boʻlsin va chekli chegara boʻlsin.

\[ \theta = \lim_(x \rightarrow a+0) \frac(f(x))(g(x)), \quad \theta \neq 0, \, +\infty. \]

Keyin integrallar

\[ \int _a^(b)f(x)dx, \quad \int _a^(b)g(x)dx \]

bir vaqtning o'zida birlashish yoki ajralish.