Медиана математическая статистика. Структурные характеристики вариационного ряда распределения

Медианой Ме называют такое значение признака, которое приходится на середину ранжированного ряда и делит его на две равные по числу единиц части. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака, превышающие медиану, другая – меньше медианы.

Медиану используют вместо средней арифметической, когда крайние варианты ранжированного ряда (наименьшая и наибольшая) по сравнению с остальными оказываются чрезмерно большими или чрезмерно малыми.

В дискретном вариационном ряду, содержащем нечетное число единиц, медиана равна варианте признака, имеющей номер :
,
где N – число единиц совокупности.
В дискретном ряду, состоящем из четного числа единиц совокупности, медиана определяется как средняя из вариант, имеющих номера и :
.
В распределении рабочих по стажу работы медиана равна средней из вариант, имеющих в ранжированном ряду номера 10: 2 = 5 и 10: 2 + 1 = 6. Варианты пятого и шестого признака равны 4 годам, таким образом
года
При вычислении медианы в интервальном ряду сначала находят медианный интервал , (т. е. содержащий медиану), для чего используют накопленные частоты или частости. Медианным является интервал, накопленная частота которого равна или превышает половину всего объема совокупности. Затем значение медианы рассчитывается по формуле:
,
где – нижняя граница медианного интервала;
– ширина медианного интервала;
– накопленная частота интервала, предшествующего медианному;
– частота медианного интервала.
Рассчитаем медиану ряда распределения рабочих по размеру зарплаты (см. лекцию «Сводка и группировка статистических данных»).
Медианным является интервал заработной платы 800-900 грн., поскольку его кумулятивная частота равна 17, что превышает половину суммы всех частот (). Тогда
Ме=800+100грн.
Полученное значение говорит о том, половина рабочих имеют заработную плату ниже 875 грн., но это выше среднего ее размера.
Для определения медианы можно вместо кумулятивных частот использовать кумулятивные частости .
Медиана, как и мода, не зависит от крайних значений вариант, поэтому также применяется для характеристики центра в рядах распределения с неопределенными границами.
Свойство медианы :сумма абсолютных величин отклонений вариант от медианы меньше, чем от любой другой величины (в том числе и от средней арифметической):

Это свойство медианы используется на транспорте при проектировании расположения трамвайных и троллейбусных остановок, бензоколонок, сборочных пунктов и т..д.
Пример. На шоссе длиной 100 км расположено 10 гаражей. Для проектирования строительства бензоколонки были собраны данные о числе предполагаемых ездок на заправку по каждому гаражу.
Таблица 2 – Данные о количестве ездок на заправку по каждому гаражу.

Нужно поставить бензоколонку так, чтобы общий пробег автомашин на заправку был наименьшим.
Вариант 1. Если бензоколонку поставить в середине шоссе, т. е. на 50-ом километре (центр диапазона изменения признака), то пробеги с учетом числа ездок составят:
а) в одном направлении:
;
б) в противоположном:
;
в) общий пробег в оба направления: .

Вариант 2. Если бензоколонку поставить на среднем участке шоссе, определенном по формуле средней арифметической с учетом числа ездок:

Медиану можно определить графически, по кумуляте (см. лекцию «Сводка и группировка статистических данных»). Для этого последнюю ординату, равную сумме всех частот или частостей, делят пополам. Из полученной точки восстанавливают перпендикуляр до пересечения с кумулятой. Абсцисса точки пересечения и дает значение медианы.

КОНТРОЛЬНАЯ РАБОТА

На тему: "Мода. Медиана. Способы их расчета"

Введение

Средние величины и связанные с ними показатели вариации играют в статистике очень большую роль, что обусловлено предметом ее изучения. Поэтому данная тема является одной из центральных в курсе.

Средняя является очень распространенным обобщающим показателям в статистике. Это объясняется тем, что только с помощью средней можно охарактеризовать совокупность по количественно варьирующему признаку. Средней величиной в статистике называется обобщающая характеристика совокупности однотипных явлений по какому-либо количественно варьирующему признаку. Средняя показывает уровень этого признака, отнесенный к единице совокупности.

Изучая общественные явления и стремясь выявить их характерные, типичные черты в конкретных условиях места и времени, статистики широко используют средние величины. С помощью средних можно сравнивать между собой различные совокупности по варьирующим признакам.

Средние, которые применяются в статистике, относятся к классу степенных средних. Из степенных средних наиболее часто применяется средняя арифметическая, реже – средняя гармоническая; средняя гармоническая применяется только при исчислении средних темпов динамики, а средняя квадратическая – только при исчислении показателей вариации.

Средняя арифметическая есть частное от деления суммы вариант на их число. Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности образуется как сумма значений признака у отдельных ее единиц. Средняя арифметическая – наиболее распространенный вид средних, так как она соответствует природе общественных явлений, где объем варьирующих признаков в совокупности чаще всего образуется именно как сумма значений признака у отдельных единиц совокупности.

По своему определяющему свойству средняя гармоническая должна применяться тогда, когда общий объем признака образуется как сумма обратных значений вариант. Ее применяют тогда, когда в зависимости от имеющего материала веса приходиться не умножать, а делить на варианты или, что то же самое, умножать на обратное их значение. Средняя гармоническая в этих случаях – это величина обратная средней арифметической из обратных значений признака.

К средней гармонической следует прибегать в тех случаях, когда в качестве весов применяются не единицы совокупности – носители признака, а произведения этих единиц на значение признака.

1. Определение моды и медианы в статистике

Средние арифметическая и гармоническая являются обобщающими характеристиками совокупности по тому или иному варьирующему признаку. Вспомогательными описательными характеристиками распределения варьирующего признака являются мода и медиана.

Модой в статистике называется величина признака (варианта), которая чаще всего встречается в данной совокупности. В вариационном ряду это будет варианта, имеющая наибольшую частоту.

Медианной в статистике называется варианта, которая находится в середине вариационного ряда. Медиана делит ряд пополам, по обе стороны от нее (вверх и вниз) находится одинаковое количество единиц совокупности.

Мода и медиана в отличии от степенных средних являются конкретными характеристиками, их значение имеет какая-либо конкретная варианта в вариационном ряду.

Мода применяется в тех случаях, когда нужно охарактеризовать наиболее часто встречающуюся величину признака. Если надо, например, узнать наиболее распространенный размер заработной платы на предприятии, цену на рынке, по которой было продано наибольшее количество товаров, размер ботинок, пользующийся наибольшим спросом у потребителей, и т.д., в этих случаях прибегают к моде.

Медиана интересна тем, что показывает количественную границу значение варьирующего признака, которую достигла половина членов совокупности. Пусть средняя заработная плата работников банка составила 650000 руб. в месяц. Эта характеристика может быть дополнена, если мы скажем, что половина работников получила заработную плату 700000 руб. и выше, т.е. приведем медиану. Мода и медиана являются типичными характеристиками в тех случаях, когда взяты совокупности однородные и большой численности.

2. Нахождение моды и медианы в дискретном вариационном ряду

Найти моду и медиану в вариационном ряду, где значения признака заданы определенными числами, не представляет большой трудности. Рассмотрим таблицу 1. с распределение семей по числу детей.

Таблица 1. Распределение семей по числу детей

Очевидно, в этом примере модой будет семья, имеющая двоих детей, так как этому значению варианты соответствует наибольшее число семей. Могут быть распределения, где все варианты встречаются одинаково часто, в этом случае моды нет или, иначе, можно сказать, что все варианты одинаково модальны. В других случаях не одна, а две варианты могут быть наибольшей частоты. Тогда будет две моды, распределение будет бимодальным. Бимодальные распределения могут указывать на качественную неоднородность совокупности по исследуемому признаку.

Чтобы найти медиану в дискретном вариационном ряд, нужно сумму частот разделить пополам и к полученному результату добавить ½. Так, в распределении 185 семьи по числу детей медианой будет: 185/2 + ½ = 93, т.е. 93-я варианта, которая делит упорядоченный ряд пополам. Каково же значение 93-ей варианты? Для того чтобы это выяснить, нужно накапливать частоты, начиная, от наименьшей варианты. Сумма частот 1-й и 2-й вариант равна 40. Ясно, что здесь 93 варианты нет. Если прибавить к 40 частоту 3-й варианты, то получим сумму, равную 40 + 75 = 115. Следовательно, 93-я варианта соответствует третьему значению варьирующего признака, и медианой будет семья, имеющая двоих детей.

Мода и медиана в данном примере совпали. Если бы у нас была четная сумма частот (например, 184), то, применяя указанную выше формулу, получим номер медианной варианты, 184/2 + ½ =92,5. Поскольку варианты с дробным номером не существует, полученный результат указывает, что медиана находится посередине между 92 и 93 вариантами.

3. Расчет моды и медианы в интервальном вариационном ряду

Описательный характер моды и медианы связан с тем, что в них не погашаются индивидуальные отклонения. Они всегда соответствуют определенной варианте. Поэтому мода и медиана не требуют для своего нахождения расчетов, если известны все значения признака. Однако в интервальном вариационном ряду для нахождения приближенного значения моды и медианы в пределах определенного интервала прибегают к расчетам.

Для расчета определенного значения модальной величины признака, заключенного в интервале, применяют формулу:

М о = Х Мо + i Мо *(f Мо – f Мо-1)/((f Мо – f Мо-1) + (f Мо – f Мо+1)),

Где Х Мо – минимальная граница модального интервала;

i Мо – величина модального интервала;

f Мо – частота модального интервала;

f Мо-1 – частота интервала, предшествующего модальному;

f Мо+1 – частота интервала, следующего за модальным.

Покажем расчет моды на примере, приведенном в таблице 2.

Таблица 2. Распределение рабочих предприятия по выполнению норм выработки

Чтобы найти моду, первоначально определим модальный интервал данного ряда. Из примера видно, что наибольшая частота соответствует интервалу, где варианта лежит в пределах от 100 до 105. Это и есть модальный интервал. Величина модального интервала равна 5.

Подставляя числовые значения из таблицы 2. в указанную выше формулу, получим:

М о = 100 + 5 * (104 -12)/((104 – 12) + (104 – 98)) = 108,8

Смысл этой формулы заключается в следующем: величину той части модального интервала, которую нужно добавить к его минимальной границе, определяют в зависимости от величины частот предшествующего и последующего интервалов. В данном случае к 100 прибавляем 8,8, т.е. больше половины интервала, потому что частота предшествующего интервала меньше частоты последующего интервала.

Исчислим теперь медиану. Для нахождения медианы в интервальном вариационном ряду определяем сначала интервал, в котором она находится (медианный интервал). Таким интервалом будет такой, комулятивная частота которого равна или превышает половину суммы частот. Комулятивные частоты образуются путем постепенного суммирования частот, начиная от интервала с наименьшим значением признака. Половина суммы частот у нас равна 250 (500:2). Следовательно, согласно таблицы 3. медианным интервалом будет интервал со значением заработной платы от 350000 руб. до 400000 руб.

Таблица 3. Расчет медианы в интервальном вариационном ряду

До этого интервала сумма накопленных частот составила 160. Следовательно, чтобы получить значение медианы, необходимо прибавить еще 90 единиц (250 – 160).

Мода и медиана – особого рода средние, которые используются для изучения структуры вариационного ряда. Их иногда называют структурными средними, в отличие от рассмотренных ранее степенных средних.

Мода – это величина признака (варианта), которая чаще всего встречается в данной совокупности, т.е. имеет наибольшую частоту.

Мода имеет большое практическое применение и в ряде случаев только мода может дать характеристику общественных явлений.

Медиана – это варианта, которая находится в середине упорядоченного вариационного ряда.

Медиана показывает количественную границу значения варьирующего признака, которой достигла половина единиц совокупности. Применение медианы наряду со средней или вместо нее целесообразно при наличии в вариационном ряду открытых интервалов, т.к. для вычисления медианы не требуется условное установление границ отрытых интервалов, и поэтому отсутствие сведений о них не влияет на точность вычисления медианы.

Медиану применяют также тогда, когда показатели, которые нужно использовать в качестве весов, неизвестны. Медиану применяют вместо средней арифметической при статистических методах контроля качества продукции. Сумма абсолютных отклонений варианты от медианы меньше, чем от любого другого числа.

Рассмотрим расчет моды и медианы в дискретном вариационном ряду:

Определить моду и медиану.

Мода Мо = 4 года, так как этому значению соответствует наибольшая частота f = 5.

Т.е. наибольшее число рабочих имеют стаж 4 года.

Для того, чтобы вычислить медиану, найдем предварительно половину суммы частот. Если сумма частот является числом нечетным, то мы сначала прибавляем к этой сумме единицу, а затем делим пополам:

Медианой будет восьмая по счету варианта.

Для того, чтобы найти, какая варианта будет восьмой по номеру, будем накапливать частоты до тех пор, пока не получим сумму частот, равную или превышающую половину суммы всех частот. Соответствующая варианта и будет медианой.

Ме = 4 года.

Т.е. половина рабочих имеет стаж меньше четырех лет, половина больше.

Если сумма накопленных частот против одной варианты равна половине сумме частот, то медиана определяется как средняя арифметическая этой варианты и последующей.

Вычисление моды и медианы в интервальном вариационном ряду

Мода в интервальном вариационном ряду вычисляется по формуле

где Х М0 - начальная граница модального интервала,

h м 0 – величина модального интервала,

f м 0 , f м 0-1 , f м 0+1 – частота соответственно модального интервала, предшествующего модальному и последующего.

Модальным называется такой интервал, которому соответствует наибольшая частота.

Пример 1

Определить моду и медиану.

Модальный интервал , т.к. ему соответствует наибольшая частота f = 35. Тогда:

Хм 0 =6, fм 0 =35

Функция МЕДИАНА в Excel используется для анализа диапазона числовых значений и возвращает число, которое является серединой исследуемого множества (медианой). То есть, данная функция условно разделяет множество чисел на два подмножества, первое из которых содержит числа меньше медианы, а второе – больше. Медиана является одним из нескольких методов определения центральной тенденции исследуемого диапазона.

Примеры использования функции МЕДИАНА в Excel

При исследовании возрастных групп студентов использовались данные случайно выбранной группы учащихся в ВУЗе. Задача – определить срединный возраст студентов.

Исходные данные:

Формула для расчета:

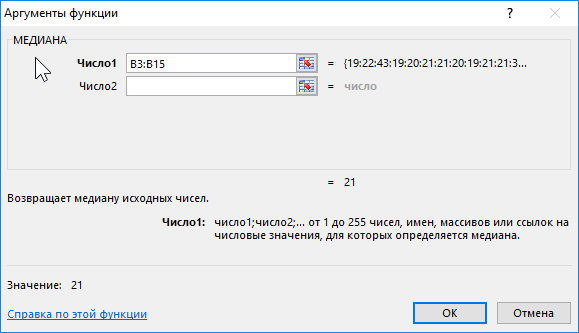
Описание аргумента:

• B3:B15 – диапазон исследуемых возрастов.

Полученный результат:

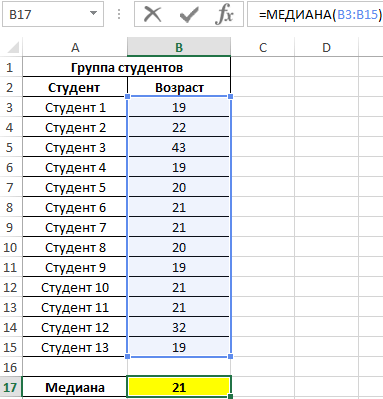
То есть в группе есть студенты, возраст которых меньше 21 года и больше этого значения.

Сравнение функций МЕДИАНА и СРЗНАЧ для вычисления среднего значения

Во время вечернего обхода в больнице каждому больному была замерена температура тела. Продемонстрировать целесообразность использования параметра медиана вместо среднего значения для исследования ряда полученных значений.

Исходные данные:

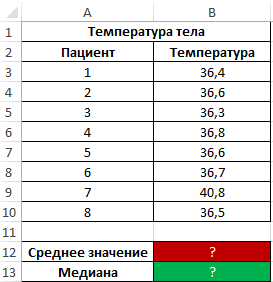
Формула для нахождения среднего значения:

Формула для нахождения медианы:

Как видно из показателя среднего значения, в среднем температура у пациентов выше нормы, однако это не соответствует действительности. Медиана показывает, что как минимум у половины пациентов наблюдается нормальная температура тела, не превышающая показатель 36,6.

Внимание! Еще одним методом определения центральной тенденции является мода (наиболее часто встречающееся значение в исследуемом диапазоне). Чтобы определить центральную тенденцию в Excel следует использовать функцию МОДА. Обратите внимание: в данном примере значения медианы и моды совпадают:

То есть срединная величина, делящая одно множество на подмножества меньших и больших значений также является и наиболее часто встречающимся значением в множестве. Как видно, у большинства пациентов температура составляет 36,6.

Пример расчета медианы при статистическом анализе в Excel

Пример 3. В магазине работают 3 продавца. По результатам последних 10 дней необходимо определить работника, которому будет выдана премия. При выборе лучшего работника учитывается степень эффективности его работы, а не число проданных товаров.

Исходная таблица данных:

Для характеристики эффективности будем использовать сразу три показателя: среднее значение, медиана и мода. Определим их для каждого работника с использованием формул СРЗНАЧ, МЕДИАНА и МОДА соответственно:

Для определения степени разброса данных используем величину, которая является суммарным значением модуля разницы среднего значения и моды, среднего значения и медианы соответственно. То есть коэффициент x=|av-med|+|av-mod|, где:

• av – среднее значение;
• med – медиана;
• mod – мода.

Рассчитаем значение коэффициента x для первого продавца:

Аналогично проведем расчеты для остальных продавцов. Полученные результаты:

Определим продавца, которому будет выдана премия:

Примечание: функция НАИМЕНЬШИЙ возвращает первое минимальное значение из рассматриваемого диапазона значений коэффициента x.

Коэффициент x является некоторой количественной характеристикой стабильности работы продавцов, которую ввел экономист магазина. С его помощью удалось определить диапазон с наименьшими отклонениями значений. Этот способ демонстрирует, как можно использовать сразу три метода определения центральной тенденции для получения наиболее достоверных результатов.

Особенности использования функции МЕДИАНА в Excel

Функция имеет следующий синтаксис:

МЕДИАНА(число1; [число2];...)

Описание аргументов:

• число1 – обязательный аргумент, характеризующий первое числовое значение, содержащееся в исследуемом диапазоне;
• [число2] – необязательный второй (и последующие аргументы, всего до 255 аргументов), характеризующий второе и последующие значения исследуемого диапазона.

Примечания 1:

1. При расчетах удобнее передавать сразу весь диапазон исследуемых значений вместо последовательного ввода аргументов.
2. В качестве аргументов принимаются данные числового типа, имена, содержащие числа, данные ссылочного типа и массивы (например, =МЕДИАНА({1;2;3;5;7;10})).
3. При расчете медианы учитываются ячейки, содержащие пустые значения или логические ИСТИНА, ЛОЖЬ, которые будут интерпретированы как числовые значения 1 и 0 соответственно. Например, результат выполнения функции с логическими значениями в аргументах (ИСТИНА;ЛОЖЬ) эквивалентен результату выполнения с аргументами (1;0) и равен 0,5.
4. Если один или несколько аргументов функции принимают текстовые значения, которые не могут быть преобразованы в числовые, или содержат коды ошибок, результатом выполнения функции будет код ошибки #ЗНАЧ!.
5. Для определения медианы выборки могут быть использованы другие функции Excel: ПРОЦЕНТИЛЬ.ВКЛ, КВАРТИЛЬ.ВКЛ, НАИБОЛЬШИЙ Примеры использования:

• =ПРОЦЕНТИЛЬ.ВКЛ(A1:A10;0,5), поскольку по определению медиана – 50-я процентиль.
• =КВАРТИЛЬ.ВКЛ(A1:A10;2), так как медиана – 2-я квартиль.
• =НАИБОЛЬШИЙ(A1:A9;СЧЁТ(A1:A9)/2), но только если количество чисел в диапазоне является нечетным числом.

Примечания 2:

1. Если в исследуемом диапазоне все числа распределены симметрично относительно среднего значения, среднее арифметическое и медиана для данного диапазона будут эквивалентны.
2. При больших отклонениях данных в диапазоне («разбросе» значений) медиана лучше отражает тенденцию распределения значений, чем среднее арифметическое. Отличным примером является использование медианы для определения реального уровня зарплат у населения государства, в котором чиновники получают на порядок больше обычных граждан.
3. Диапазон исследуемых значений может содержать:

• Нечетное количество чисел. В этом случае медианой будет являться единственное число, разделяющее диапазон на два подмножества больших и меньших значений соответственно;
• Четное количество чисел. Тогда медиана вычисляется как среднее арифметическое для двух числовых значений, разделяющих множество на два указанных выше подмножества.

Для вычисления медианы в MS EXCEL существует специальная функция МЕДИАНА() . В этой статье дадим определение медианы и научимся вычислять ее для выборки и для заданного закона распределения случайной величины.

Начнем с медианы для выборок (т.е. для фиксированного набора значений).

Медиана выборки

Медиана (median) – это число, которое является серединой множества чисел: половина чисел множества больше, чем медиана , а половина чисел меньше, чем медиана .

Для вычисления медианы необходимо сначала (значения в выборке ). Например, медианой для выборки (2; 3; 3; 4 ; 5; 7; 10) будет 4. Т.к. всего в выборке 7 значений, три из них меньше, чем 4 (т.е. 2; 3; 3), а три значения больше (т.е. 5; 7; 10).

Если множество содержит четное количество чисел, то вычисляется для двух чисел, находящихся в середине множества. Например, медианой для выборки (2; 3; 3 ; 6 ; 7; 10) будет 4,5, т.к. (3+6)/2=4,5.

Для определения медианы в MS EXCEL существует одноименная функция МЕДИАНА() , английский вариант MEDIAN().

Медиана не обязательно совпадает со . Совпадение имеет место только в том случае, если значения в выборке распределены симметрично относительно среднего . Например, для выборки (1; 2; 3 ; 4 ; 5; 6) медиана и среднее равны 3,5.

Если известна Функция распределения F(х) или функция плотности вероятности p (х) , то медиану можно найти из уравнения:

Например, решив аналитическим способом это уравнение для Логнормального распределения lnN(μ; σ 2), получим, что медиана вычисляется по формуле =EXP(μ). При μ=0, медиана равна 1.

Обратите внимание на точку Функции распределения , для которой F (х)=0,5 (см. картинку выше). Абсцисса этой точкиравна1. Это и есть значение медианы, что естественно совпадает с ранее вычисленным значением по формуле em.

В MS EXCEL медиану для логнормального распределения LnN(0;1) можно вычислить по формуле =ЛОГНОРМ.ОБР(0,5;0;1) .

Примечание : Напомним, что интеграл от по всей области задания случайной величины равен единице.

Поэтому, линия медианы (х=Медиана) делит площадь под графиком функции плотности вероятности на две равные части.