The number 0 can be represented as a kind of border separating the world of real numbers from imaginary or negative ones. Due to the ambiguous position, many operations with this numerical value do not obey mathematical logic. The impossibility of dividing by zero is a prime example of this. And allowed arithmetic operations with zero can be performed using generally accepted definitions.

History of Zero

Zero is the reference point in all standard number systems. Europeans began to use this number relatively recently, but the sages of ancient India used zero for a thousand years before the empty number was regularly used by European mathematicians. Even before the Indians, zero was a mandatory value in the Maya numerical system. This American people used the duodecimal system, and they began the first day of each month with a zero. Interestingly, among the Maya, the sign for "zero" completely coincided with the sign for "infinity". Thus, the ancient Maya concluded that these quantities were identical and unknowable.

Math operations with zero

Standard mathematical operations with zero can be reduced to a few rules.

Addition: if you add zero to an arbitrary number, then it will not change its value (0+x=x).

Subtraction: when subtracting zero from any number, the value of the subtracted remains unchanged (x-0=x).

Multiplication: any number multiplied by 0 gives 0 in the product (a*0=0).

Division: Zero can be divided by any non-zero number. In this case, the value of such a fraction will be 0. And division by zero is prohibited.

Exponentiation. This action can be performed with any number. An arbitrary number raised to the power of zero will give 1 (x 0 =1).

Zero to any power is equal to 0 (0 a \u003d 0).

In this case, a contradiction immediately arises: the expression 0 0 does not make sense.

Paradoxes of mathematics

The fact that division by zero is impossible, many people know from school. But for some reason it is not possible to explain the reason for such a ban. Indeed, why does the division-by-zero formula not exist, but other actions with this number are quite reasonable and possible? The answer to this question is given by mathematicians.

The thing is that the usual arithmetic operations that schoolchildren study in elementary grades are in fact far from being as equal as we think. All simple operations with numbers can be reduced to two: addition and multiplication. These operations are the essence of the very concept of a number, and the rest of the operations are based on the use of these two.

Addition and multiplication

Let's take a standard subtraction example: 10-2=8. At school, it is considered simply: if two are taken away from ten objects, eight remain. But mathematicians look at this operation quite differently. After all, there is no such operation as subtraction for them. This example can be written in another way: x+2=10. For mathematicians, the unknown difference is simply the number that must be added to two to make eight. And no subtraction is required here, you just need to find a suitable numerical value.

Multiplication and division are treated in the same way. In the example of 12:4=3, it can be understood that we are talking about the division of eight objects into two equal piles. But in reality, this is just an inverted formula for writing 3x4 \u003d 12. Such examples for division can be given endlessly.

Examples for dividing by 0

This is where it becomes a little clear why it is impossible to divide by zero. Multiplication and division by zero have their own rules. All examples per division of this quantity can be formulated as 6:0=x. But this is an inverted expression of the expression 6 * x = 0. But, as you know, any number multiplied by 0 gives only 0 in the product. This property is inherent in the very concept of a zero value.

It turns out that such a number, which, when multiplied by 0, gives any tangible value, does not exist, that is, this problem has no solution. One should not be afraid of such an answer, it is a natural answer for problems of this type. Just writing 6:0 doesn't make any sense, and it can't explain anything. In short, this expression can be explained by the immortal "no division by zero".

Is there a 0:0 operation? Indeed, if the operation of multiplying by 0 is legal, can zero be divided by zero? After all, an equation of the form 0x5=0 is quite legal. Instead of the number 5, you can put 0, the product will not change from this.

Indeed, 0x0=0. But you still can't divide by 0. As said, division is just the inverse of multiplication. Thus, if in the example 0x5=0, you need to determine the second factor, we get 0x0=5. Or 10. Or infinity. Dividing infinity by zero - how do you like it?

But if any number fits into the expression, then it does not make sense, we cannot choose one from an infinite set of numbers. And if so, it means that the expression 0:0 does not make sense. It turns out that even zero itself cannot be divided by zero.

higher mathematics

Division by zero is a headache for high school math. Mathematical analysis studied in technical universities slightly expands the concept of problems that have no solution. For example, to the already known expression 0:0, new ones are added that have no solution in school mathematics courses:

• infinity divided by infinity: ∞:∞;
• infinity minus infinity: ∞−∞;
• unit raised to an infinite power: 1 ∞ ;
• infinity multiplied by 0: ∞*0;
• some others.

It is impossible to solve such expressions by elementary methods. But higher mathematics, thanks to additional possibilities for a number of similar examples, gives final solutions. This is especially evident in the consideration of problems from the theory of limits.

Uncertainty Disclosure

In the theory of limits, the value 0 is replaced by a conditional infinitesimal variable. And expressions in which division by zero is obtained when substituting the desired value are converted. Below is a standard example of limit expansion using the usual algebraic transformations:

As you can see in the example, a simple reduction of a fraction brings its value to a completely rational answer.

When considering the limits of trigonometric functions, their expressions tend to be reduced to the first remarkable limit. When considering the limits in which the denominator goes to 0 when the limit is substituted, the second remarkable limit is used.

L'Hopital method

In some cases, the limits of expressions can be replaced by the limit of their derivatives. Guillaume Lopital - French mathematician, founder of the French school of mathematical analysis. He proved that the limits of expressions are equal to the limits of the derivatives of these expressions. In mathematical notation, his rule is as follows.

If a number is divided by infinity, does the quotient tend to zero? Continued inside and got a better answer

Answer from Olenka[newbie]
all 0
Krab Bark
Oracle
(56636)
No. Exact zero. As the divisor tends to infinity, the quotient tends to zero. And, if we divide not by a number tending to infinity, but by infinity itself (by the way, to be more precise, it is not officially considered a number at all, but is considered a special symbol that complements the designations of numbers) - exactly zero.

Answer from Jugeus Vladimir[guru]
Even divide zero, even multiply by any number, it will still be zero!

Answer from 1 23 [guru]
if some shit tends to zero, then multiplying it by something finite (a number or a limited function) is painless, because all-rna tends to zero.
but if you multiply it by some kind of thing that tends to endlessness, then there may be options.

Answer from Krab Bark[guru]
Dividing any number by infinity results in zero. Exact zero, no "going to zero". And then, by whatever number you multiply it, zero. And the result of dividing zero by any number other than zero will be zero, only when dividing zero by zero, the result is not defined, any number will be suitable as a quotient.

Methods for solving limits. Uncertainties.
Function growth order. Replacement Method

Example 4

Find the limit

This is a simpler example for a do-it-yourself solution. In the proposed example, again, uncertainty (of a higher order of growth than the root).

If "x" tends to "minus infinity"

The ghost of "minus infinity" has long been hovering in this article. Consider limits with polynomials in which . The principles and methods of solution will be exactly the same as in the first part of the lesson, with the exception of a number of nuances.

Consider 4 chips that will be required to solve practical tasks:

1) Calculate the limit

The value of the limit depends only on the term because it has the highest order of growth. If , then infinitely large modulo negative number to the power of EVEN, in this case - in the fourth, is equal to "plus infinity": . Constant ("two") positive, that's why:

2) Calculate the limit

Here is the senior degree again even, that's why: . But there is a "minus" in front ( negative constant –1), therefore:

3) Calculate the limit

The value of the limit depends only on . As you remember from school, "minus" "pops out" from under the odd degree, so infinitely large modulo negative number to an ODD power equals "minus infinity", in this case: .
Constant ("four") positive, means:

4) Calculate the limit

The first guy in the village has again odd degree, moreover, in the bosom negative constant, which means: Thus:
.

Example 5

Find the limit

Using the above points, we conclude that there is uncertainty here. The numerator and denominator are of the same order of growth, which means that in the limit a finite number will be obtained. We learn the answer by discarding all the fry:

The solution is trivial:

Example 6

Find the limit

This is a do-it-yourself example. Full solution and answer at the end of the lesson.

And now, perhaps the most subtle of the cases:

Example 7

Find the limit

Considering the senior terms, we come to the conclusion that there is uncertainty here. The numerator is of a higher order of growth than the denominator, so we can immediately say that the limit is infinity. But what kind of infinity, "plus" or "minus"? The reception is the same - in the numerator and denominator we will get rid of the little things:

We decide:

Divide the numerator and denominator by

Example 15

Find the limit

This is a do-it-yourself example. An approximate sample of finishing at the end of the lesson.

A couple more interesting examples on the topic of variable substitution:

Example 16

Find the limit

Substituting one into the limit results in uncertainty. The replacement of the variable is already suggesting, but first we convert the tangent using the formula. Indeed, why do we need a tangent?

Note that , therefore . If it is not entirely clear, look at the sine values ​​\u200b\u200bin trigonometric table . Thus, we immediately get rid of the factor , in addition, we get the more familiar uncertainty 0:0. It would be nice if our limit also tended to zero.

Let's replace:

If , then

Under the cosine we have "x", which also needs to be expressed through "te".
From the replacement we express: .

We complete the solution:

(1) Performing the substitution

(2) Expand the brackets under the cosine.

(4) To organize first wonderful limit , artificially multiply the numerator by and the reciprocal of .

Task for independent solution:

Example 17

Find the limit

Full solution and answer at the end of the lesson.

These were simple tasks in their class; in practice, everything is worse, and, in addition to reduction formulas, one has to use different trigonometric formulas , as well as other tricks. In the article Complex Limits I made out a couple of real examples =)

On the eve of the holiday, we will finally clarify the situation with one more common uncertainty:

Elimination of uncertainty "one to the power of infinity"

This uncertainty is “served” second wonderful limit , and in the second part of that lesson, we looked in great detail at standard examples of solutions that are found in practice in most cases. Now the picture with exhibitors will be completed, in addition, the final tasks of the lesson will be devoted to the limits-"tricks" in which it seems that it is necessary to apply the 2nd wonderful limit, although this is not at all the case.

The disadvantage of the two working formulas of the 2nd remarkable limit is that the argument must tend to "plus infinity" or to zero. But what if the argument tends to a different number?

The universal formula comes to the rescue (which is actually a consequence of the second remarkable limit):

Uncertainty can be eliminated by the formula:

Somewhere like I already explained what the square brackets mean. Nothing special, brackets are just brackets. Usually they are used to clearly highlight a mathematical notation.

Let's highlight the essential points of the formula:

1) It's about only about uncertainty and no other.

2) Argument "x" can tend to arbitrary value(and not only to zero or ), in particular, to "minus infinity" or to anyone final number.

Using this formula, you can solve all the examples of the lesson Remarkable Limits , which belong to the 2nd wonderful limit. For example, let's calculate the limit:

In this case , and according to the formula:

True, I don’t advise you to do this, in the tradition, you still use the “usual” design of the solution, if it can be applied. However using the formula is very convenient to check"classical" examples to the 2nd wonderful limit.

The derivative of the function does not fall far, and in the case of L'Hopital's rules, it falls exactly where the original function falls. This circumstance helps in revealing uncertainties of the form 0/0 or ∞/∞ and some other uncertainties arising in the calculation limit ratio of two infinitesimal or infinitely large functions. The calculation is greatly simplified by this rule (actually two rules and notes on them):

As the formula above shows, when calculating the limit of the ratio of two infinitesimal or infinitely large functions, the limit of the ratio of two functions can be replaced by the limit of the ratio of their derivatives and thus get a certain result.

Let's move on to more precise formulations of L'Hopital's rules.

L'Hopital's Rule for the Case of the Limit of Two Infinitely Small Values. Let the functions f(x) and g(x a. And at the very point a a function derivative g(x) is not equal to zero ( g"(x a are equal to each other and equal to zero:

.

L'Hôpital's rule for the case of the limit of two infinitely large quantities. Let the functions f(x) and g(x) have derivatives (that is, they are differentiable) in some neighborhood of the point a. And at the very point a they may or may not have derivatives. Moreover, in the vicinity of the point a function derivative g(x) is not equal to zero ( g"(x)≠0 ) and the limits of these functions as x tends to the value of the function at the point a are equal to each other and equal to infinity:

.

Then the limit of the ratio of these functions is equal to the limit of the ratio of their derivatives:

In other words, for uncertainties of the form 0/0 or ∞/∞, the limit of the ratio of two functions is equal to the limit of the ratio of their derivatives, if the latter exists (finite, that is, equal to a certain number, or infinite, that is, equal to infinity).

Remarks.

1. L'Hopital's rules are also applicable when the functions f(x) and g(x) are not defined at x = a.

2. If, when calculating the limit of the ratio of derivatives of functions f(x) and g(x) we again come to an uncertainty of the form 0/0 or ∞/∞, then L'Hopital's rules should be applied repeatedly (at least twice).

3. L'Hopital's rules are also applicable when the argument of the functions (x) tends to a non-finite number a, and to infinity ( x → ∞).

Uncertainties of other types can also be reduced to uncertainties of the types 0/0 and ∞/∞.

Disclosure of uncertainties of the types "zero divided by zero" and "infinity divided by infinity"

Example 1

x=2 leads to an indeterminacy of the form 0/0. Therefore, the derivative of each function and we get

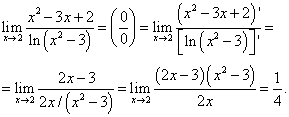
In the numerator, the derivative of the polynomial was calculated, and in the denominator - derivative of a complex logarithmic function. Before the last equal sign, the usual limit, substituting a deuce instead of x.

Example 2 Calculate the limit of the ratio of two functions using L'Hospital's rule:

Solution. Substitution into a given value function x

Example 3 Calculate the limit of the ratio of two functions using L'Hospital's rule:

Solution. Substitution into a given value function x=0 leads to an indeterminacy of the form 0/0. Therefore, we calculate the derivatives of the functions in the numerator and denominator and get:

Example 4 Calculate

Solution. Substituting the value of x equal to plus infinity into a given function leads to an indeterminacy of the form ∞/∞. Therefore, we apply L'Hopital's rule:

Comment. Let's move on to examples in which the L'Hopital rule has to be applied twice, that is, to come to the limit of the ratio of the second derivatives, since the limit of the ratio of the first derivatives is an uncertainty of the form 0/0 or ∞/∞.

Disclosure of uncertainties of the form "zero multiplied by infinity"

Example 12. Calculate

.

Solution. We get

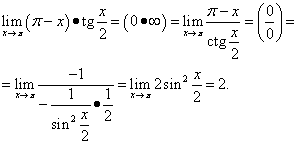
This example uses the trigonometric identity.

Disclosure of uncertainties of the types "zero to the power of zero", "infinity to the power of zero" and "one to the power of infinity"

Uncertainties of the form , or are usually reduced to the form 0/0 or ∞/∞ using the logarithm of a function of the form

To calculate the limit of the expression, one should use the logarithmic identity, a special case of which is the property of the logarithm .

Using the logarithmic identity and the continuity property of the function (to go beyond the sign of the limit), the limit should be calculated as follows:

Separately, one should find the limit of the expression in the exponent and build e to the found degree.

Example 13

Solution. We get

.

.

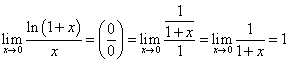Example 14 Calculate using L'Hopital's rule

Solution. We get

Calculate the limit of the expression in the exponent

.

.

Example 15 Calculate using L'Hopital's rule