Methods for solving limits. Uncertainties.
Function growth order. Replacement Method

Example 4

Find the limit

This is a simpler example for a do-it-yourself solution. In the proposed example, again, uncertainty (of a higher order of growth than the root).

If "x" tends to "minus infinity"

The ghost of "minus infinity" has long been hovering in this article. Consider limits with polynomials in which . The principles and methods of solution will be exactly the same as in the first part of the lesson, with the exception of a number of nuances.

Consider 4 chips that will be required to solve practical tasks:

1) Calculate the limit

The value of the limit depends only on the term because it has the highest order of growth. If , then infinitely large modulo negative number to the power of EVEN, in this case - in the fourth, is equal to "plus infinity": . Constant ("two") positive, that's why:

2) Calculate the limit

Here is the senior degree again even, that's why: . But in front there is a "minus" ( negative constant –1), therefore:

3) Calculate the limit

The value of the limit depends only on . As you remember from school, "minus" "pops out" from under the odd degree, so infinitely large modulo negative number to an ODD power equals "minus infinity", in this case: .
Constant ("four") positive, means:

4) Calculate the limit

The first guy in the village has again odd degree, moreover, in the bosom negative constant, which means: Thus:
.

Example 5

Find the limit

Using the above points, we conclude that there is uncertainty here. The numerator and denominator are of the same order of growth, which means that in the limit a finite number will be obtained. We learn the answer by discarding all the fry:

The solution is trivial:

Example 6

Find the limit

This is a do-it-yourself example. Full solution and answer at the end of the lesson.

And now, perhaps the most subtle of the cases:

Example 7

Find the limit

Considering the senior terms, we come to the conclusion that there is uncertainty here. The numerator is of a higher order of growth than the denominator, so we can immediately say that the limit is infinity. But what kind of infinity, "plus" or "minus"? The reception is the same - in the numerator and denominator we will get rid of the little things:

We decide:

Divide the numerator and denominator by

Example 15

Find the limit

This is a do-it-yourself example. An example of a finishing touch at the end of the lesson.

A couple more interesting examples on the topic of variable substitution:

Example 16

Find the limit

Substituting one into the limit results in uncertainty. The replacement of the variable is already suggesting, but first we convert the tangent using the formula. Indeed, why do we need tangent?

Note that , therefore . If it is not entirely clear, look at the sine values ​​\u200b\u200bin trigonometric table. Thus, we immediately get rid of the factor , in addition, we get the more familiar uncertainty 0:0. It would be nice if our limit also tended to zero.

Let's replace:

If , then

Under the cosine we have "x", which also needs to be expressed through "te".
From the replacement we express: .

We complete the solution:

(1) Performing the substitution

(2) Expand the brackets under the cosine.

(4) To organize first wonderful limit, artificially multiply the numerator by and the reciprocal of .

Task for independent solution:

Example 17

Find the limit

Full solution and answer at the end of the lesson.

These were simple tasks in their class; in practice, everything is worse, and, in addition to reduction formulas, one has to use different trigonometric formulas, as well as other tricks. In the article Complex Limits, I analyzed a couple of real examples =)

On the eve of the holiday, we will finally clarify the situation with one more common uncertainty:

Elimination of uncertainty "one to the power of infinity"

This uncertainty is “served” second wonderful limit, and in the second part of that lesson, we looked in great detail at standard examples of solutions that are found in practice in most cases. Now the picture with exhibitors will be completed, in addition, the final tasks of the lesson will be devoted to the limits-"tricks" in which it seems that it is necessary to apply the 2nd wonderful limit, although this is not at all the case.

The disadvantage of the two working formulas of the 2nd wonderful limit is that the argument must tend to "plus infinity" or to zero. But what if the argument tends to a different number?

The universal formula comes to the rescue (which is actually a consequence of the second remarkable limit):

Uncertainty can be eliminated by the formula:

Somewhere like I have already explained what the square brackets mean. Nothing special, brackets are just brackets. Usually they are used to clearly highlight a mathematical notation.

Let's highlight the essential points of the formula:

1) It's about only about uncertainty and no other.

2) Argument "x" can tend to arbitrary value(and not only to zero or ), in particular, to "minus infinity" or to anyone final number.

Using this formula, you can solve all the examples of the lesson Remarkable Limits, which belong to the 2nd wonderful limit. For example, let's calculate the limit:

In this case , and according to the formula :

True, I don’t advise you to do this, in the tradition, you still use the “usual” design of the solution, if it can be applied. However using the formula is very convenient to check"classical" examples to the 2nd wonderful limit.

If a number is divided by infinity, does the quotient tend to zero? Continued inside and got a better answer

Answer from Olenka[newbie]
all 0
Krab Bark
Oracle
(56636)
No. Exact zero. As the divisor tends to infinity, the quotient tends to zero. And, if we divide not by a number tending to infinity, but by infinity itself (by the way, to be more precise, it is not officially considered a number at all, but is considered a special symbol that complements the designations of numbers) - exactly zero.

Answer from Jugeus Vladimir[guru]
Even divide zero, even multiply by any number, it will still be zero!

Answer from 1 23 [guru]
if some kind of crap tends to zero, then multiplying it by something finite (a number or a limited function) is painless, because all-rna tends to zero.
but if you multiply it by some kind of thing that tends to endlessness, then there may be options.

Answer from Krab Bark[guru]
Dividing any number by infinity results in zero. Exact zero, no "going to zero". And then, by whatever number you multiply it, zero. And the result of dividing zero by any number other than zero will be zero, only when dividing zero by zero, the result is not defined, any number will be suitable as a quotient.

Very often, many people wonder why it is impossible to use division by zero? In this article, we will go into great detail about where this rule came from, as well as what actions can be performed with zero.

In contact with

Zero can be called one of the most interesting numbers. This number has no meaning, it means emptiness in the truest sense of the word. However, if zero is placed next to any digit, then the value of this digit will become several times larger.

The number is very mysterious in itself. It was used by the ancient Mayan people. For the Maya, zero meant "beginning", and the countdown of calendar days also started from zero.

A very interesting fact is that the sign of zero and the sign of uncertainty were similar for them. By this, the Maya wanted to show that zero is the same identical sign as uncertainty. In Europe, the designation of zero appeared relatively recently.

Also, many people know the prohibition associated with zero. Any person will say that cannot be divided by zero. This is what teachers at school say, and children usually take their word for it. Usually, children are either simply not interested in knowing this, or they know what will happen if, having heard an important prohibition, they immediately ask “Why can’t we divide by zero?”. But when you get older, interest awakens, and you want to know more about the reasons for such a ban. However, there is reasonable evidence.

Actions with zero

First you need to determine what actions can be performed with zero. Exists several types of activities:

• Addition;
• Multiplication;
• Subtraction;
• Division (zero by number);
• Exponentiation.

Important! If zero is added to any number during addition, then this number will remain the same and will not change its numerical value. The same thing happens if you subtract zero from any number.

With multiplication and division, things are a little different. If a multiply any number by zero, then the product will also become zero.

Consider an example:

Let's write this as an addition:

There are five added zeros in total, so it turns out that

Let's try to multiply one by zero. The result will also be null.

Zero can also be divided by any other number not equal to it. In this case, it will turn out, the value of which will also be zero. The same rule applies to negative numbers. If you divide zero by a negative number, you get zero.

You can also raise any number to zero power. In this case, you get 1. It is important to remember that the expression "zero to the zero power" is absolutely meaningless. If you try to raise zero to any power, you get zero. Example:

We use the multiplication rule, we get 0.

Is it possible to divide by zero

So, here we come to the main question. Is it possible to divide by zero generally? And why is it impossible to divide a number by zero, given that all other operations with zero fully exist and apply? To answer this question, you need to turn to higher mathematics.

Let's start with the definition of the concept, what is zero? School teachers claim that zero is nothing. Emptiness. That is, when you say that you have 0 pens, it means that you have no pens at all.

In higher mathematics, the concept of "zero" is broader. It doesn't mean empty at all. Here, zero is called uncertainty, because if we do a little research, it turns out that when we divide zero by zero, we can get any other number as a result, which may not necessarily be zero.

Do you know that those simple arithmetic operations that you studied at school are not so equal among themselves? The most basic steps are addition and multiplication.

For mathematicians, the concepts of "" and "subtraction" do not exist. Let's say: if three are subtracted from five, then two will remain. This is what subtraction looks like. However, mathematicians would write it this way:

Thus, it turns out that the unknown difference is a certain number that needs to be added to 3 to get 5. That is, you don’t need to subtract anything, you just need to find a suitable number. This rule applies to addition.

Things are a little different with multiplication and division rules. It is known that multiplication by zero leads to zero result. For example, if 3:0=x, then if you flip the record, you get 3*x=0. And the number that is multiplied by 0 will give zero in the product. It turns out that a number that would give any value other than zero in the product with zero does not exist. This means that division by zero is meaningless, that is, it fits our rule.

But what happens if you try to divide zero by itself? Let's take x as some indefinite number. It turns out the equation 0 * x \u003d 0. It can be solved.

If we try to take zero instead of x, we get 0:0=0. It would seem logical? But if we try to take any other number instead of x, for example, 1, then we end up with 0:0=1. The same situation will be if you take any other number and plug it into the equation.

In this case, it turns out that we can take any other number as a factor. The result will be an infinite number of different numbers. Sometimes, nevertheless, division by 0 in higher mathematics makes sense, but then usually there is a certain condition due to which we can still choose one suitable number. This action is called "uncertainty disclosure". In ordinary arithmetic, division by zero will again lose its meaning, since we will not be able to choose any one number from the set.

Important! Zero cannot be divided by zero.

Zero and infinity

Infinity is very common in higher mathematics. Since it is simply not important for schoolchildren to know that there are still mathematical operations with infinity, teachers cannot properly explain to children why it is impossible to divide by zero.

Students begin to learn the basic mathematical secrets only in the first year of the institute. Higher mathematics provides a large set of problems that have no solution. The most famous problems are the problems with infinity. They can be solved with mathematical analysis.

You can also apply to infinity elementary mathematical operations: addition, multiplication by a number. Subtraction and division are also commonly used, but in the end they still come down to two simple operations.

But what will if you try:

• Multiply infinity by zero. In theory, if we try to multiply any number by zero, we will get zero. But infinity is an indefinite set of numbers. Since we cannot choose one number from this set, the expression ∞*0 has no solution and is absolutely meaningless.
• Zero divided by infinity. This is the same story as above. We can’t choose one number, which means we don’t know what to divide by. The expression doesn't make sense.

Important! Infinity is a little different from uncertainty! Infinity is a type of uncertainty.

Now let's try to divide infinity by zero. It would seem that there should be uncertainty. But if we try to replace division with multiplication, we get a very definite answer.

For example: ∞/0=∞*1/0= ∞*∞ = ∞.

It turns out like this mathematical paradox.

Why you can't divide by zero

Thought experiment, try to divide by zero

Conclusion

So, now we know that zero is subject to almost all operations that are performed with, except for one single one. You can't divide by zero just because the result is uncertainty. We also learned how to operate on zero and infinity. The result of such actions will be uncertainty.

The derivative of the function does not fall far, and in the case of L'Hospital's rules, it falls exactly where the original function falls. This circumstance helps in revealing uncertainties of the form 0/0 or ∞/∞ and some other uncertainties that arise in the calculation limit ratio of two infinitesimal or infinitely large functions. The calculation is greatly simplified by this rule (actually two rules and notes on them):

As the formula above shows, when calculating the limit of the ratio of two infinitesimal or infinitely large functions, the limit of the ratio of two functions can be replaced by the limit of the ratio of their derivatives and thus get a certain result.

Let's move on to more precise formulations of L'Hopital's rules.

L'Hopital's Rule for the Case of the Limit of Two Infinitely Small Values. Let the functions f(x) and g(x a. And at the very point a a function derivative g(x) is not equal to zero ( g"(x a are equal to each other and equal to zero:

.

L'Hôpital's rule for the case of the limit of two infinitely large quantities. Let the functions f(x) and g(x) have derivatives (that is, they are differentiable) in some neighborhood of the point a. And at the very point a they may or may not have derivatives. Moreover, in the vicinity of the point a function derivative g(x) is not equal to zero ( g"(x)≠0 ) and the limits of these functions as x tends to the value of the function at the point a are equal to each other and equal to infinity:

.

Then the limit of the ratio of these functions is equal to the limit of the ratio of their derivatives:

In other words, for uncertainties of the form 0/0 or ∞/∞, the limit of the ratio of two functions is equal to the limit of the ratio of their derivatives, if the latter exists (finite, that is, equal to a certain number, or infinite, that is, equal to infinity).

Remarks.

1. L'Hopital's rules are also applicable when the functions f(x) and g(x) are not defined at x = a.

2. If, when calculating the limit of the ratio of derivatives of functions f(x) and g(x) we again come to an uncertainty of the form 0/0 or ∞/∞, then L'Hopital's rules should be applied repeatedly (at least twice).

3. L'Hopital's rules are also applicable when the argument of the functions (x) tends to a non-finite number a, and to infinity ( x → ∞).

Uncertainties of other types can also be reduced to uncertainties of the types 0/0 and ∞/∞.

Disclosure of uncertainties of the types "zero divided by zero" and "infinity divided by infinity"

Example 1

x=2 leads to an indeterminacy of the form 0/0. Therefore, the derivative of each function and we get

In the numerator, the derivative of the polynomial was calculated, and in the denominator - derivative of a complex logarithmic function. Before the last equal sign, the usual limit, substituting a deuce instead of x.

Example 2 Calculate the limit of the ratio of two functions using L'Hopital's rule:

Solution. Substitution into a given value function x

Example 3 Calculate the limit of the ratio of two functions using L'Hopital's rule:

Solution. Substitution into a given value function x=0 leads to an indeterminacy of the form 0/0. Therefore, we calculate the derivatives of the functions in the numerator and denominator and get:

Example 4 Calculate

Solution. Substituting the value of x equal to plus infinity into a given function leads to an indeterminacy of the form ∞/∞. Therefore, we apply L'Hopital's rule:

Comment. Let's move on to examples in which the L'Hopital rule has to be applied twice, that is, to come to the limit of the ratio of the second derivatives, since the limit of the ratio of the first derivatives is an uncertainty of the form 0/0 or ∞/∞.

Disclosure of uncertainties of the form "zero multiplied by infinity"

Example 12. Calculate

.

Solution. We get

This example uses the trigonometric identity.

Disclosure of uncertainties of the types "zero to the power of zero", "infinity to the power of zero" and "one to the power of infinity"

Uncertainties of the form , or are usually reduced to the form 0/0 or ∞/∞ using the logarithm of a function of the form

To calculate the limit of the expression, one should use the logarithmic identity, a special case of which is the property of the logarithm .

Using the logarithmic identity and the continuity property of the function (to go beyond the sign of the limit), the limit should be calculated as follows:

Separately, one should find the limit of the expression in the exponent and build e to the found degree.

Example 13.

Solution. We get

.

.

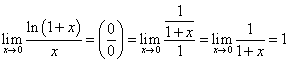Example 14 Calculate using L'Hopital's rule

Solution. We get

Calculate the limit of the expression in the exponent

.

.

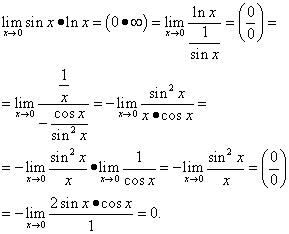Example 15 Calculate using L'Hopital's rule

The main elementary functions have been sorted out.

When moving to functions of a more complex form, we will definitely encounter expressions whose value is not defined. Such expressions are called uncertainties.

Let's list everything main types of uncertainties: zero divided by zero (0 by 0), infinity divided by infinity, zero times infinity, infinity minus infinity, one to the power of infinity, zero to the power of zero, infinity to the power of zero.

ALL OTHER EXPRESSIONS ARE NOT UNCERTAINTY AND TAKE A COMPLETELY SPECIFIC FINITE OR INFINITE VALUE.

Reveal Uncertainties allows:

• simplification of the type of function (transformation of an expression using abbreviated multiplication formulas, trigonometric formulas, multiplication by conjugate expressions with subsequent reduction, etc.);
• use of remarkable limits;
• application of L'Hospital's rule;
• the use of replacing an infinitesimal expression with its equivalent (using a table of equivalent infinitesimals).

We group the uncertainties into uncertainty table. For each type of uncertainty, we put in correspondence the method of its disclosure (the method of finding the limit).

This table, together with the table of limits of the basic elementary functions, will be your main tools in finding any limits.

Let's give a couple of examples when everything is immediately obtained after substituting the value and uncertainty does not arise.

Example.

Calculate Limit

Solution.

We substitute the value:

And we got an answer right away.

Answer:

Example.

Calculate Limit

Solution.

We substitute the value x=0 into the base of our exponential power function:

That is, the limit can be rewritten as

Now let's take a look at the index. This is a power function. Let us turn to the table of limits for power functions with a negative exponent. From there we have and , therefore, we can write .

Based on this, our limit can be written as:

Again we turn to the table of limits, but for exponential functions with a base greater than one, from which we have:

Answer:

Let's look at examples with detailed solutions disclosure of ambiguities by transforming expressions.

Very often, the expression under the limit sign needs to be slightly transformed to get rid of ambiguities.

Example.

Calculate Limit

Solution.

We substitute the value:

Came to uncertainty. We look at the table of uncertainties to choose a solution method. Let's try to simplify the expression.

Answer:

Example.

Calculate Limit

Solution.

We substitute the value:

Came to uncertainty (0 by 0). We look at the table of uncertainties to select a solution method and try to simplify the expression. We multiply both the numerator and the denominator by the expression conjugate to the denominator.

For the denominator, the adjoint expression is

We multiplied the denominator so that we could apply the abbreviated multiplication formula - the difference of squares and then reduce the resulting expression.

After a series of transformations, the uncertainty disappeared.

Answer:

COMMENT: for limits of this kind, the method of multiplication by conjugate expressions is typical, so feel free to use it.

Example.

Calculate Limit

Solution.

We substitute the value:

Came to uncertainty. We look at the table of uncertainties to select a solution method and try to simplify the expression. Since both the numerator and denominator vanish at x=1, if these expressions can be reduced (x-1) and the uncertainty will disappear.

Let's factorize the numerator:

Let's factorize the denominator:

Our limit will take the form:

After the transformation, the uncertainty was revealed.

Answer:

Consider the limits at infinity of power expressions. If the exponents of the exponential expression are positive, then the limit at infinity is infinite. Moreover, the main value has the greatest degree, the rest can be discarded.

Example.

Example.

If the expression under the limit sign is a fraction, and both the numerator and the denominator are power expressions (m is the power of the numerator, and n is the power of the denominator), then when there is an uncertainty of the form infinity by infinity, in this case uncertainty is revealed division and numerator and denominator by

Example.

Calculate Limit