Числото 0 може да бъде представено като вид граница, разделяща света на реалните числа от въображаемите или отрицателните. Поради нееднозначната позиция, много операции с тази числена стойност не се подчиняват на математическата логика. Невъзможността за деление на нула е отличен пример за това. И разрешените аритметични операции с нула могат да се извършват с помощта на общоприети дефиниции.

История на нулата

Нулата е референтната точка във всички стандартни бройни системи. Европейците започнаха да използват това число сравнително наскоро, но мъдреците от древна Индия използваха нула в продължение на хиляда години, преди празното число да се използва редовно от европейските математици. Още преди индианците нулата е била задължителна стойност в числовата система на маите. Този американски народ използваше дванадесетичната система и започваше първия ден от всеки месец с нула. Интересното е, че при маите знакът за "нула" напълно съвпадал със знака за "безкрайност". Така древните маи заключили, че тези количества са идентични и непознаваеми.

Математически операции с нула

Стандартните математически операции с нула могат да бъдат сведени до няколко правила.

Добавяне: ако добавите нула към произволно число, то няма да промени стойността си (0+x=x).

Изваждане: при изваждане на нула от което и да е число, стойността на изваденото остава непроменена (x-0=x).

Умножение: всяко число, умножено по 0, дава 0 в продукта (a*0=0).

Деление: Нулата може да бъде разделена на всяко различно от нула число. В този случай стойността на такава фракция ще бъде 0. И разделянето на нула е забранено.

степенуване. Това действие може да се извърши с произволен номер. Произволно число, повдигнато на степен нула, ще даде 1 (x 0 =1).

Нула на произволна степен е равна на 0 (0 a = 0).

В този случай веднага възниква противоречие: изразът 0 0 няма смисъл.

Парадокси на математиката

Фактът, че разделянето на нула е невъзможно, много хора знаят от училище. Но по някаква причина не е възможно да се обясни причината за такава забрана. Наистина, защо формулата за деление на нула не съществува, но други действия с това число са съвсем разумни и възможни? Отговорът на този въпрос е даден от математиците.

Работата е там, че обичайните аритметични операции, които учениците изучават в началните класове, всъщност далеч не са толкова равни, колкото си мислим. Всички прости операции с числа могат да бъдат сведени до две: събиране и умножение. Тези операции са същността на самата концепция за число, а останалите операции се основават на използването на тези две.

Събиране и умножение

Нека вземем стандартен пример за изваждане: 10-2=8. В училище се смята просто: ако от десет обекта се отнемат две, остават осем. Но математиците гледат на тази операция съвсем различно. В крайна сметка за тях няма такава операция като изваждане. Този пример може да бъде написан по друг начин: x+2=10. За математиците неизвестната разлика е просто числото, което трябва да се добави към две, за да се получи осем. И тук не се изисква изваждане, просто трябва да намерите подходяща числена стойност.

Умножението и делението се третират по същия начин. В примера за 12:4=3 може да се разбере, че говорим за разделянето на осем обекта на две равни купчини. Но в действителност това е просто обърната формула за писане на 3x4 \u003d 12. Такива примери за разделяне могат да се дават безкрайно.

Примери за деление на 0

Тук става донякъде ясно защо е невъзможно да се дели на нула. Умножението и делението с нула имат свои собствени правила. Всички примери за деление на това количество могат да бъдат формулирани като 6:0=x. Но това е обърнат израз на израза 6 * x = 0. Но, както знаете, всяко число, умножено по 0, дава в продукта само 0. Това свойство е присъщо на самата концепция за нулева стойност.

Оказва се, че такова число, което, умножено по 0, дава някаква осезаема стойност, не съществува, тоест тази задача няма решение. Човек не трябва да се страхува от такъв отговор, той е естествен отговор за проблеми от този тип. Самото писане на 6:0 няма никакъв смисъл и не може да обясни нищо. Накратко, този израз може да се обясни с безсмъртното "без деление на нула".

Има ли операция 0:0? Наистина, ако операцията за умножение по 0 е законна, може ли нулата да бъде разделена на нула? В края на краищата, уравнение от формата 0x5=0 е съвсем законно. Вместо числото 5 можете да поставите 0, продуктът няма да се промени от това.

Наистина, 0x0=0. Но все още не можете да разделите на 0. Както казахме, делението е просто обратното на умножението. Така, ако в примера 0x5=0, трябва да определите втория фактор, получаваме 0x0=5. Или 10. Или безкрайност. Деление на безкрайност на нула - как ви харесва?

Но ако някое число се побере в израза, то няма смисъл, не можем да изберем едно от безкраен набор от числа. И ако е така, това означава, че изразът 0:0 няма смисъл. Оказва се, че дори самата нула не може да бъде разделена на нула.

висша математика

Деленето на нула е главоболие за математиката в гимназията. Математическият анализ, изучаван в техническите университети, леко разширява концепцията за проблеми, които нямат решение. Например към вече познатия израз 0:0 се добавят нови, които нямат решение в училищните курсове по математика:

• безкрайност разделена на безкрайност: ∞:∞;
• безкрайност минус безкрайност: ∞−∞;
• единица, повдигната на безкрайна степен: 1 ∞ ;
• безкрайност, умножена по 0: ∞*0;
• някои други.

Невъзможно е да се решат такива изрази с елементарни методи. Но висшата математика, благодарение на допълнителните възможности за редица подобни примери, дава окончателни решения. Това е особено очевидно при разглеждането на проблеми от теорията на границите.

Разкриване на несигурност

В теорията на границите стойността 0 се заменя с условна безкрайно малка променлива. И се преобразуват изрази, в които се получава деление на нула при заместване на желаната стойност. По-долу е даден стандартен пример за разширяване на лимита с помощта на обичайните алгебрични трансформации:

Както можете да видите в примера, просто намаляване на дроб довежда нейната стойност до напълно рационален отговор.

Когато се разглеждат границите на тригонометричните функции, техните изрази са склонни да бъдат намалени до първата забележителна граница. Когато се разглеждат границите, в които знаменателят отива до 0, когато границата се замести, се използва втората забележителна граница.

Метод L'Hopital

В някои случаи границите на изразите могат да бъдат заменени с границата на техните производни. Гийом Лопитал – френски математик, основател на френската школа по математически анализ. Той доказа, че границите на изразите са равни на границите на производните на тези изрази. В математическата нотация неговото правило е следното.

Ако едно число се дели на безкрайност, клони ли частното към нула? Продължих вътре и получих по-добър отговор

Отговор от Оленка [новак]
всички 0
Краб кора
Оракул
(56636)
Не. Точна нула. Тъй като делителят клони към безкрайност, частното клони към нула. И ако разделим не на число, клонящо към безкрайност, а на самата безкрайност (между другото, за да бъдем по-точни, то изобщо не се счита официално за число, а се счита за специален символ, който допълва обозначенията на числата) - точно нула.

Отговор от Югеус Владимир[гуру]
Дори да разделите нула, дори да умножите по произволно число, пак ще бъде нула!

Отговор от 1 23 [гуру]
ако някои неща клонят към нула, тогава умножаването им по нещо крайно (число или ограничена функция) е безболезнено, защото all-rna клони към нула.
но ако го умножите по нещо, което клони към безкрайност, тогава може да има опции.

Отговор от Краб кора[гуру]
Разделянето на произволно число на безкрайност води до нула. Точна нула, без „стигане до нула“. И след това, по каквото и число да го умножите, нула. И резултатът от разделянето на нула на всяко число, различно от нула, ще бъде нула, само когато разделяте нула на нула, резултатът не е дефиниран, всяко число ще бъде подходящо като частно.

Методи за решаване на граници. Несигурности.
Ред на нарастване на функцията. Метод на замяна

Пример 4

Намерете границата

Това е по-опростен пример за решение „направи си сам“. В предложения пример, отново, несигурност (от по-висок порядък на растеж от корена).

Ако "x" клони към "минус безкрайност"

Призракът на "минус безкрайността" отдавна витае в тази статия. Помислете за граници с полиноми, в които . Принципите и методите на решение ще бъдат абсолютно същите като в първата част на урока, с изключение на редица нюанси.

Помислете за 4 чипа, които ще са необходими за решаване на практически задачи:

1) Изчислете границата

Стойността на лимита зависи само от срока, тъй като той има най-висок ред на нарастване. Ако , тогава безкрайно голям модулотрицателно число на ЧЕТНА степен, в случая - в четвъртата, е равно на "плюс безкрайност": . Постоянно ("две") положителен, Ето защо:

2) Изчислете границата

Ето я отново висшата степен дори, Ето защо: . Но има "минус" отпред ( отрицателенконстанта –1), следователно:

3) Изчислете границата

Стойността на лимита зависи само от. Както си спомняте от училище, "минус" "изскача" изпод нечетната степен, така че безкрайно голям модулотрицателно число на НЕЧЕТНА степене равно на "минус безкрайност", в този случай: .
Постоянно ("четири") положителен, означава:

4) Изчислете границата

Първият момък в селото отново има странностепен, при това в пазвата отрицателенконстанта, което означава: Така:
.

Пример 5

Намерете границата

Използвайки горните точки, заключаваме, че тук има несигурност. Числителят и знаменателят са от един и същ ред на нарастване, което означава, че в ограничението ще се получи крайно число. Научаваме отговора, като изхвърлим цялото пържене:

Решението е тривиално:

Пример 6

Намерете границата

Това е пример за „направи си сам“. Пълно решение и отговор в края на урока.

И сега, може би най-финият от случаите:

Пример 7

Намерете границата

Имайки предвид старшите условия, стигаме до извода, че тук има несигурност. Числителят е от по-висок порядък на растеж от знаменателя, така че веднага можем да кажем, че границата е безкрайност. Но каква безкрайност, "плюс" или "минус"? Рецепцията е същата - в числителя и знаменателя ще се отървем от малките неща:

Ние решаваме:

Разделете числителя и знаменателя на

Пример 15

Намерете границата

Това е пример за „направи си сам“. Приблизителна проба за завършване в края на урока.

Още няколко интересни примера по темата за заместване на променливи:

Пример 16

Намерете границата

Заместването на едно в границата води до несигурност. Замяната на променливата вече предполага, но първо преобразуваме тангенса с помощта на формулата. Наистина, защо се нуждаем от допирателна?

Отбележете, че следователно. Ако не е напълно ясно, погледнете синусовите стойности в тригонометрична таблица . Така незабавно се отърваваме от фактора , освен това получаваме по-познатата несигурност 0:0. Би било хубаво, ако нашата граница също клонеше към нула.

Да заменим:

Ако , тогава

Под косинуса имаме "x", което също трябва да бъде изразено чрез "te".
От замяната изразяваме: .

Завършваме решението:

(1) Извършване на замяната

(2) Разгънете скобите под косинуса.

(4) Да организира първата прекрасна граница , изкуствено умножете числителя по и реципрочната на .

Задача за самостоятелно решение:

Пример 17

Намерете границата

Пълно решение и отговор в края на урока.

Това бяха прости задачи в техния клас; на практика всичко е по-лошо и в допълнение към формули за намаляване, човек трябва да използва различни тригонометрични формули , както и други трикове. В статията Комплексни границиНаправих няколко реални примера =)

В навечерието на празника най-накрая ще изясним ситуацията с още една често срещана неизвестност:

Елиминиране на несигурността "едно на степен на безкрайност"

Тази несигурност се „сервира“ втора прекрасна граница , а във втората част на този урок разгледахме много подробно стандартни примери за решения, които се срещат на практика в повечето случаи. Сега картината с изложители ще бъде завършена, освен това последните задачи на урока ще бъдат посветени на границите-"трикове", в които изглежда, че е необходимо да се приложи втората прекрасна граница, въпреки че това изобщо не е случай.

Недостатъкът на двете работещи формули на втората забележителна граница е, че аргументът трябва да клони към "плюс безкрайност" или към нула. Но какво ще стане, ако аргументът клони към различно число?

На помощ идва универсалната формула (която всъщност е следствие от второто забележително ограничение):

Несигурността може да се елиминира по формулата:

Някъде, както вече обясних какво означават квадратните скоби. Нищо особено, скобите са си просто скоби. Обикновено те се използват за ясно подчертаване на математическа нотация.

Нека подчертаем основните точки на формулата:

1) Става въпрос за само за несигурността и нищо друго.

2) Аргументът "x" може да клони към произволна стойност(и не само до нула или), по-специално до "минус безкрайност" или до всекикрайно число.

Използвайки тази формула, можете да решите всички примери от урока Забележителни граници , които спадат към 2-ра забележителна граница. Например, нека изчислим лимита:

В такъв случай , и по формулата:

Вярно е, че не ви съветвам да правите това, по традиция все още използвате „обичайния“ дизайн на решението, ако може да се приложи. въпреки това използването на формулата е много удобно за проверка"класически" примери до 2-ра прекрасна граница.

Производната на функцията не пада далеч и в случая с правилата на L'Hopital тя попада точно там, където пада оригиналната функция. Това обстоятелство помага за разкриването на несигурности от формата 0/0 или ∞/∞ и някои други несигурности, възникващи при изчислението лимитсъотношение на две безкрайно малки или безкрайно големи функции. Изчислението е значително опростено от това правило (всъщност две правила и бележки към тях):

Както показва формулата по-горе, когато се изчислява границата на съотношението на две безкрайно малки или безкрайно големи функции, границата на съотношението на две функции може да бъде заменена с границата на съотношението на техните производнии по този начин да получите определен резултат.

Нека да преминем към по-точни формулировки на правилата на L'Hopital.

Правилото на L'Hopital за случай на граница на две безкрайно малки стойности. Нека функциите f(х) и ж(х а. И то в самата точка а апроизводна на функция ж(х) не е равно на нула ( ж"(х аса равни помежду си и равни на нула:

.

Правилото на L'Hôpital за случай на граница на две безкрайно големи количества. Нека функциите f(х) и ж(х) имат производни (т.е. те са диференцируеми) в някаква околност на точката а. И то в самата точка ате могат или не могат да имат производни. При това в околностите на пункта апроизводна на функция ж(х) не е равно на нула ( ж"(х)≠0 ) и границите на тези функции, когато x клони към стойността на функцията в точката аса равни помежду си и равни до безкрайност:

.

Тогава границата на съотношението на тези функции е равна на границата на съотношението на техните производни:

С други думи, за несигурности от формата 0/0 или ∞/∞, границата на съотношението на две функции е равна на границата на съотношението на техните производни, ако последното съществува (крайно, т.е. равно на a определено число или безкрайно, тоест равно на безкрайност).

Забележки.

1. Правилата на L'Hopital са приложими и когато функциите f(х) и ж(х) не са дефинирани в х = а.

2. Ако при изчисляване на границата на отношението на производните на функциите f(х) и ж(х) отново стигаме до несигурност от формата 0/0 или ∞/∞, тогава правилата на L'Hopital трябва да се прилагат многократно (поне два пъти).

3. Правилата на L'Hopital са приложими и когато аргументът на функциите (x) клони към некрайно число аи до безкрайност ( х → ∞).

Несигурностите от други видове също могат да бъдат сведени до несигурности от типа 0/0 и ∞/∞.

Разкриване на несигурности от типа "нула, разделена на нула" и "безкрайност, разделена на безкрайност"

Пример 1

х=2 води до неопределеност на формата 0/0. Следователно, производната на всяка функция и ние получаваме

В числителя се изчислява производната на полинома, а в знаменателя - производна на комплексна логаритмична функция. Преди последния знак за равенство, обичайното лимит, замествайки двойка вместо x.

Пример 2Изчислете границата на отношението на две функции, като използвате правилото на L'Hospital:

Решение. Заместване във функция с дадена стойност х

Пример 3Изчислете границата на отношението на две функции, като използвате правилото на L'Hospital:

Решение. Заместване във функция с дадена стойност х=0 води до неопределеност на формата 0/0. Следователно изчисляваме производните на функциите в числителя и знаменателя и получаваме:

Пример 4Изчисли

Решение. Заместването на стойността на x, равна на плюс безкрайност, в дадена функция води до неопределеност под формата ∞/∞. Затова прилагаме правилото на L'Hopital:

Коментирайте. Нека да преминем към примери, в които правилото на L'Hopital трябва да се приложи два пъти, тоест да се стигне до границата на съотношението на вторите производни, тъй като границата на съотношението на първите производни е несигурност на формата 0/0 или ∞/∞.

Разкриване на несигурности от формата "нула, умножена по безкрайност"

Пример 12.Изчисли

.

Решение. Получаваме

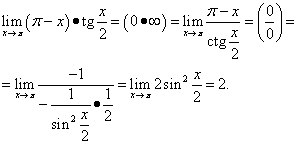
Този пример използва тригонометричната идентичност.

Разкриване на несигурности от типа "нула на степен нула", "безкрайност на степен нула" и "един на степен безкрайност"

Несигурностите на формата или обикновено се редуцират до формата 0/0 или ∞/∞, като се използва логаритъм на функция от формата

За да се изчисли границата на израза, трябва да се използва логаритмичното тъждество, чийто специален случай е свойството на логаритъма .

Като се използва логаритмичната идентичност и свойството за непрекъснатост на функцията (за преминаване отвъд знака на границата), границата трябва да се изчисли, както следва:

Отделно трябва да се намери границата на израза в експонента и да се изгради ддо намерената степен.

Пример 13

Решение. Получаваме

.

.

Пример 14Изчислете с помощта на правилото на L'Hopital

Решение. Получаваме

Изчислете границата на израза в степента

.

.

Пример 15Изчислете с помощта на правилото на L'Hopital